基于控制力矩陀螺的BTT飞行器协调转弯控制
2017-11-20赵坤曹登庆黄文虎
赵坤, 曹登庆, 黄文虎
哈尔滨工业大学 航天学院, 哈尔滨 150001
基于控制力矩陀螺的BTT飞行器协调转弯控制
赵坤, 曹登庆*, 黄文虎
哈尔滨工业大学 航天学院, 哈尔滨 150001
针对倾斜转弯 (BTT) 飞行器进行横向机动时会产生侧滑角的问题,提出一种考虑通道耦合因素的协调转弯控制方法。采用了一种基于单框控制力矩陀螺(SGCMG)的侧滑角抑制执行机构来替代方向舵、矢量推力发动机等传统执行机构。建立了加装控制力矩陀螺的BTT飞行器横向机动时的多变量强耦合非线性倾斜转弯动力学模型。根据BTT飞行器横向机动时的协调转弯要求,设计了一种基于非线性反馈和线性二次型最优算法的解耦综合控制器。计算结果表明:协调转弯控制系统可实现滚转角指令的良好跟踪和侧滑角的有效抑制。
倾斜转弯(BTT)飞行器; 协调转弯; 控制力矩陀螺; 侧滑角抑制; 非线性反馈; 线性二次型调节器
随着导弹防御技术的发展,远程高超声速滑翔飞行器 (Hypersonic Glide Vehicle, HGV) 需要具备一定的机动能力。倾斜转弯 (Bank-To-Turn, BTT)控制技术是用来提升飞行器机动性能的一个重要方法。当HGV采用BTT控制技术进行机动飞行时,飞行器的最大升力面随着滚转指令迅速地转到理想的机动方向,转弯的向心力由升力提供。由于HGV的飞行包线大,强耦合、强非线性,滚转机动时横侧向的稳定性问题尤为突出。美国对HGV的飞行稳定性开展了大量的试验研究,2010和2011年两次飞行试验均告失败的HTV-2,在飞行过程中偏航超出预期,飞行稳定性与操纵性不足,出现滚转/偏航耦合运动,远超过飞行器姿态控制系统的调节能力,导致姿态失控[1]。
目前HGV的姿态控制主要采用舵面控制、矢量推力控制以及变质心控制等。气动舵面控制是一种非常成熟的技术,但其仍存在一些问题如舵面的高温烧蚀、大迎角下控制效率下降等[2]。研究显示:X-43飞行器从迎角为8° 起纵向稳定性和舵面的横向控制效率随着迎角的增加而下降,当迎角大于20° 时,舵面效率完全丧失[3]。推力矢量控制具有响应速度快、机动性强等优点[4-5],但侧喷发动机产生的控制力大小和工作时间受飞行器携带燃料的限制。变质心控制能够保持飞行器良好的气动外形,也不会产生控制执行机构的烧蚀问题。然而HGV进入临近空间时,由于大气密度较低,因此进行大幅度的机动极为困难[6-7]。单框控制力矩陀螺(Single Gimbal Control Moment Gyro, SGCMG) 是卫星上常用的一种姿态控制执行机构[8],其利用小幅的框架运动就能产生较大的力矩输出。它不依赖于外部环境,动态响应特性好,也适用于对机动能力有较高要求的飞行器的姿态控制。如何利用SGCMG进行高机动飞行器的姿态控制,在国际上仅处于概念研究阶段,而国内已进行了一些探索性的研究[9-10]。
HGV通常采用乘波构型,由于其细长比较大,滚转通道的转动惯量较小,横侧向的运动稳定性差。当HGV进行滚转机动时,滚转响应迅速,而偏航和滚转恢复力矩和阻尼力矩较小,导致飞行器的实际滚转轴偏向于机体轴,运动耦合非常突出。与此同时,运动耦合导致侧滑角和迎角发生变化,激发出更为严重的气动耦合。因此,亟待开展HGV机动飞行时的侧滑角抑制方法的研究。这里提出了一种基于控制力矩陀螺的侧滑角抑制执行机构,充分发挥控制力矩陀螺的优点,用较小的输入力矩可获得放大的输出力矩来抑制飞行器的偏航运动。该执行机构安装方便,占用空间小,能够产生很好的侧滑角抑制效果。
要实现HGV的侧向机动,还需设计使飞行器偏航通道与滚转通道协调动作的控制系统,以达到侧滑角为零的目的[11]。由于HGV的飞行速度、高度和范围都变化较大,系统参数之间耦合严重,是一个多变量强耦合的非线性系统[12]。传统的各通道间独立设计的方法不能满足协调控制的要求,而非线性控制方法能够达到理想的控制效果。反馈线性化方法是目前开展高超声速飞行器控制系统设计常采用的一种方法[13]。本文将采用副翼和SGCMG分别作为滚转通道和偏航通道的控制执行机构,采用反馈线性化和线性二次型调节器(Linear Quadratic Regulator, LQR)最优算法设计飞行器的解耦综合控制器,以实现对期望姿态的良好跟踪。最后,通过仿真验证SGCMG在飞行器姿态机动控制应用中的可行性。
1 非线性反馈的基本理论
考虑以下多输入多输出仿射非线性系统[14]:

(1)
式中:x∈Rn为系统的状态变量;u∈Rm为系统的输入向量;y∈Rm为系统输出向量;f(x)为n维光滑向量场;G(x)=[g1(x)g2(x) …gm(x)]T,h(x)=[h1(x)h2(x) …hm(x)]T分别为n×m阶矩阵和m维向量。
定义 若式(1)所示的系统满足如下条件:

2)m×m阶矩阵
在x=x0处非奇异。则系统式(1)在x0处的相对阶向量为[r1r2…rm],其中ri为子相对阶与输出yi=hi(x)一一对应。
状态反馈精确线性化定理 假设矩阵G(x0)的秩为m,那么存在点x0的一个邻域U和定义在U上的m维输出函数h(x)使得式(1)在点x0有相对阶向量[r1r2…rm],且满足r1+r2+…+rm=n的充分必要条件是:
1) 对每个0≤i≤n-1,分布Gi在x0附近有常数维。
2) 分布Gn-1有维数n。
3) 分布Gi对合。

图1给出了r=n情况下的状态反馈精确线性化的设计原理。如果式(1)所示的MIMO仿射非线性系统的总相对阶为r1+r2+…+rm=n,则选择如下的坐标变换z=Φ(x),即
(2)
再施加相应的反馈控制:
u=α(x)+β(x)v=D(x)-1(-b(x)+v)
(3)

图1 状态反馈精确线性化原理图Fig.1 Principle of exact linearization of state feedback
(4)
式中:A、B和C均为具有适当维数的实矩阵。
2 数学模型
2.1 SGCMG模型
控制力矩陀螺是指飞轮转速不变的框架动量轮,它具有力矩放大的作用,因此控制效率很高[15]。如图2所示,设SGCMG的框架坐标系为Oxfyfzf,Oxf轴为外框架转轴,Ozf轴为转子的自转轴。Oxyz为机体坐标系,其坐标原点为飞行器质心O。Ox轴为飞行器纵轴,指向头部;Oy轴在飞行器的主对称面内;Oz轴垂直于主对称面,构成右手直角坐标系。Oxvyvzv为原点固连于飞行器质心O的速度坐标系。Oxv轴沿飞行器的速度方向;Oyv轴在飞行器的主对称面内,垂直于Oxv;Ozv轴垂直于xvOyv平面,构成右手直角坐标系。设飞行器在惯性空间中的转动角速度在Oxyz坐标系的投影为ω=[ωxωyωz]。机体坐标系和速度坐标系之间的欧拉角分别为迎角α和侧滑角β。


图2 单框控制力矩陀螺(SGCMG)模型 Fig.2 Model of Single Gimbal Control Moment Gyro(SGCMG)
如图3所示,机体坐标系Oxyz绕Ox轴转动δc角度为框架坐标系Oxfyfzf,框架坐标系绕着Ozf轴转动φ角度后为转子坐标系Oxryrzr。将机体的角速度ω投影到Oxfyfzf中,得到该系下转子的合角速度ωf,且
(5)
则转子对O点的动量矩hf在坐标系Oxfyfzf中可表示为hf=[JωxfJωyfIωzf]。忽略框架对坐标系Oxfyfzf各轴的动量矩,设转子受到的合外力矩在坐标系Oxfyfzf内的投影为mf,根据动量矩定理,在框架坐标系内有

(6)
式(6)即是陀螺相对于框架坐标系Oxfyfzf的动力学方程[16]。由于转子的转速ω0很高,引入理想约束条件:
(7)

(8)

图3 角速度的矢量合成关系Fig.3 Vector synthesis of angular velocity
式中:mxf、myf和mzf分别为合力矩mf在框架坐标系Oxfyfzf上的分量,h0=Iω0为陀螺的动量矩。显然,若以Oxf轴为输入轴,输入力矩mxf使陀螺进动,则在Oyf轴将会有力矩myf输出。将式(8)中的输出力矩myf投影到机体坐标系Oxyz中,则
(9)
SGCMG的力矩输出能力与陀螺的动量矩h0成正比,即转子的转动惯量或转速越大其输出力矩越大;同时,控制力矩陀螺的输出力矩大小与绕框架轴旋转的角速度成正比,即单位时间内从框架轴输入的控制力矩越大,其输出的力矩也越大。根据式(9),若在框架坐标系Oxfyfzf输入力矩mxf,SGCMG会分别在Oy和Oz两个轴向输出力矩my和mz。如图2所示,my可用来抑制飞行器滚转机动产生的偏航运动,但对于Oz轴向的力矩mz将会引起飞行器的俯仰运动,不利于后期的控制器设计。
使用单个SGCMG存在通道间的耦合作用,考虑采用双SGCMG的设计方案,如图4所示。选用两个结构参数完全一致的SGCMG,两者的框架轴互相平行,转子的旋转速率相等但旋转方向相反。因此两个SGCMG在Oz轴上的输出力矩互相抵消,而在Oy轴上的输出力矩互相叠加,成为以前的2倍。因此在机体坐标系Oxyz下双陀螺的动力学方程为
(10)
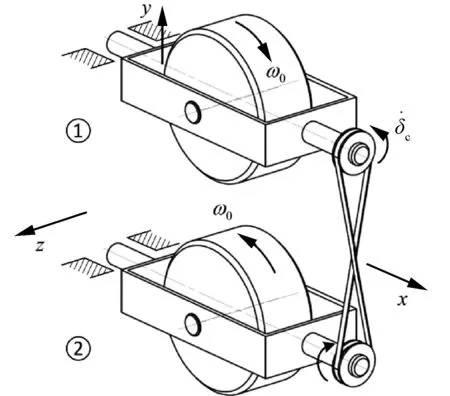
图4 侧滑角抑制装置模型Fig.4 Model of suppression device for sideslip angle
由式(10)可知,该设计方案通过物理途径实现了通道间的解耦。两个SGCMG配合工作,增强了偏航力矩的输出,同时抵消了对飞行器俯仰和滚转的干扰。两支单框控制力矩陀螺一组构成侧滑角抑制装置是最为简洁的结构设计方案。
2.2 BTT飞行器的姿态运动模型
BTT飞行器动力学建模的详细过程参见文献[17]。选取状态变量X=[αβγωxωyωz]T,其中α、β和γ分别为飞行器的迎角、侧滑角和滚转角。飞行器的姿态动力学方程如式(11)所示,式中变量均以弧度为单位。
(11)
式中:a1~a5、b1~b5、c1和c3均为飞行器的气动系数,它们均受到气动参数、大气密度和飞行器速度等的影响;Ixx、Iyy和Izz分别为飞行器绕机体轴Ox、Oy和Oz的转动惯量;δx、δy和δz分别为导弹的副翼舵、方向舵和升降舵偏角。本文只研究飞行器在短周期内的姿态控制,认为飞行器的速度、气动系数、质量和转动惯量均为定值。
飞行器滚转机动一般有两种方式:绕机体轴滚转和绕速度轴滚转。飞行器绕机体轴滚转会产生运动耦合,ωxα和-ωxβ即运动交叉耦合项。运动耦合导致侧滑角和迎角相互转换,从而引起气动交叉耦合,严重时致使飞行器失去控制。而飞行器绕速度轴滚转时,虽然可以避免运动耦合,但会产生惯性耦合,(Izz-Ixx)ωxωz/Iyy和(Ixx-Iyy)ωxωy/Izz即惯性交叉耦合项。实际的滚转机动过程中,由于飞行器自身静稳定性力矩的存在,阻碍了侧滑角和迎角的相互转换,使得飞行器的滚转轴向机体轴偏离,而飞行器实际的滚转轴介于机体轴和速度轴之间。因此飞行器实际滚转中运动耦合与惯性耦合是并存的,但运动耦合占主导地位。这样,协调控制设计考虑的主要是运动学交叉耦合项ωxα和-ωxβ,滚转控制中应集中解决运动耦合问题。
2.3 联合动力学方程
对于高超声速滑翔飞行器的再入飞行控制而言,其俯仰通道为独立的[18]。不考虑俯仰通道和惯性耦合的影响,建立的高超声速滑翔飞行器与SGCMG装置联合的倾斜转弯动力学方程为
(12)
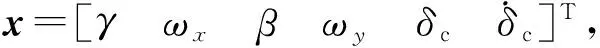
(13)
式中:p=2h0/Iyy;q=h0/J;w=1/J。在设计HGV的协调控制系统时,期望滚转角γ能够准确迅速地跟踪滚转指令信号γc,同时偏航方向的侧滑角β保持为零以实现协调转弯。因此,系统的输出向量为
(14)
3 控制器设计
反馈线性化是近些年来发展较快的一种非线性控制方法[19-21]。其基本的设计思路是将原系统中的非线性部分通过全状态反馈方法进行变换,使得变换后新系统的输入和输出之间全部为线性关系。针对新系统则可采用一般的线性系统控制理论进行控制律的设计。
3.1 非线性状态反馈控制律的建立
根据第1节的定义,式(13)和式(14)所示的非线性系统在x0=0的邻域存在以下条件:
(15)
行列式|D(x)|=c2prcosx5在x0=0处不等于0,D(x)非奇异。系统的相对阶为r1=2,r2=3,系统的总相对阶r=r1+r2=5。由于系统状态变量的维数n=6大于系统总相对阶,因此不能直接进行精确反馈线性化。此时需要根据状态反馈精确线性化定理判断该系统是否满足状态反馈精确线性化定理的条件。

根据第1节中的状态反馈精确线性化定理可知,存在一个小于或等于n的整数ε使得dim(Gε-2) (16) 而且m1=m,通过求解式(16),即可得到满足要求的虚拟输出函数λ1(x)和λ2(x)。将式(16)展开后可得 (17) 将式(17)所示的偏微分方程组看做是关于未知函数λi(x)偏导数的线性方程组,不难检验 (18) 可满足式(18)。于是,在x0=0的邻域内有 (19) 行列式|D(x)|=-(b1b4+b2)c2αprcosx5在x0=0处不等于0,D(x)非奇异,由此可得系统的相对阶为r1=3,r2=3满足系统总相对阶等于系统状态变量维数的条件。选取输出函数λ1(x)和λ2(x),然后根据式(2)采用如下的坐标变换z=Φ(x),即 (20) 然后根据式(3)可以得到相应的反馈控制律为 u= (21) 该非线性系统可以在坐标变换z=Φ(x)和反馈控制u=α(x)+β(x)v的作用下,转化为一个由新状态变量z描述的形如式(4)的线性系统。其中A、B和C分别为线性化系统的状态矩阵、控制矩阵和输出矩阵。展开后得 (22) 显然式(22)为线性系统的可控标准型。控制律v(t)可通过一般的线性系统控制原理进行设计。对式(20)进行坐标反变换,得到系统的输出函数 y= (23) 式中:飞行器的迎角α≠0。在实际飞行中,BTT飞行器的迎角α可能等于0,式(23)中的输出矩阵将产生奇异。因此,需要对α=0的情况进行专门地讨论。即令仿射非线性系统式(13)中α=0,然后对得到的新系统重复本节的过程进行非线性状态反馈控制律的设计,本文在此不展开讨论。 根据线性最优跟踪系统理论,对式(22)线性定常系统,期望设计的控制系统能够使实际输出向量y(t)尽量跟踪标准输出向量ys(t),误差向量定义为 e(t)=ys(t)-y(t) (24) 线性最优控制算法的设计目的在于寻找控制向量v(t)使误差向量取最小。一般可用式(25)表示二次型性能指标。 (25) 式中:Q为m×m维半正定的状态加权矩阵;R为m×m维正定的控制加权矩阵。该二次型性能指标的物理含义在于通过设计的控制向量v,以极小的控制能量为代价,使误差e(t)保持在零附近。根据LQR理论,使性能指标式(25)极小的最优控制为 v(t)=-R-1BTPz(t)+R-1BTg (26) 式中:P为n×n维对称正定常数矩阵,满足如下黎卡提矩阵代数方程: PA+ATP-PBR-1BTP+CTQC=0 (27) 伴随向量 (28) 最后将v(t)代入式(21),即可得到最终的解耦综合控制器。 通用航空器是一种高升阻比的升力体高超声速滑翔飞行器,飞行器质量约为 544.3~907.2 kg[22]。设置高超声速滑翔飞行器的参数为:飞行器的质量m=600 kg,转动惯量I=diag(50.1,100,100) kg·m2。设计SGCMG的转子半径为0.1 m,厚度为0.05 m,钢质材料,经计算转子的质量为12.25 kg。而整个侧滑角抑制装置约占飞行器总体质量的4.082%,满足工程实用性要求。相对于框架轴的转动惯量为0.03 kg·m2,转子的转速为5 000 r/min。采用双SGCMG的侧滑角抑制执行机构方案,如图4所示。 为验证采用控制力矩陀螺作为侧滑角抑制执行机构方法的有效性,仿真计算的初始条件及相关约束条件选取如表1所示。由式(10)可知,当框架角为0° 时,控制力矩陀螺的力矩输出能力最强。控制力矩陀螺的输出力矩my随框架角δc的增大而减小,当框架角超过45° 后力矩输出能力衰减迅速,这就需要较大的输入力矩η,增加了系统的负担。考虑到BTT飞行器实际的工作状况,设定副翼舵偏角和控制力矩陀螺框架角的控制指令约束为 -30°≤δx≤30°, -45°≤δc≤45° (29) 表1 飞行器初始状态Table 1 Initial state of vehicle 姿态控制律采用式(21)的形式,选取系统的状态加权矩阵Q=diag(1.0,1.0),控制加权矩阵R=diag(0.01,0.01)。仿真结果如图5~图7所示。 图5 侧滑角的时间历程曲线Fig.5 History of sideslip angle 图6 单框控制力矩陀螺的操纵律Fig.6 Control law of SGCMG 图7 输出力矩和输入力矩的对比Fig.7 Comparison of output torque and input torque 图5显示,进入稳态后侧滑角β的稳态误差小于0.1°,采用控制力矩陀螺取得了良好的侧滑角控制效果,通过调节Q和R可以进一步改善系统的输出响应。由图6给出的控制力矩陀螺操纵律的变化曲线可以看出,框架角在-16°≤δc≤16° 范围内变化,陀螺转子绕框架轴Oxf反复变向以起到对侧滑角进行调节的目的。当侧滑角达到稳态值0° 附近后,框架角δc也恢复到0° 附近,保持最大的力矩输出能力。图7给出了控制力矩陀螺的输出力矩和输入力矩,最大输入力矩ηmax=49.90 N·m,而最大输出控制力矩Mmax=176.75 N·m,力矩放大倍数N约为3.5。力矩放大倍数N可通过加权矩阵R进行调控。 在系统方程式(12)中的侧滑角通道引入外部干扰d=0.1sin(2πt),单位为rad/s。仿真结果如图8和图9所示。在外部扰动的作用下,控制力矩陀螺通过不断地进动来抑制侧滑角的变化。 图8 扰动情况下侧滑角的时间历程曲线Fig.8 History of sideslip angle under disturbance 图9 角速度的对比Fig.9 Contrast between angular velocities 控制稳定后侧滑角基本维持在0° 附近波动,波动幅度小于0.5°,控制系统具有较强的抗干扰能力。 下面将在前述非线性状态反馈控制律设计的基础上验证控制器的协调性。对给定的侧滑角指令βc=0°,滚转角γc设为交变的方波指令信号,仿真结果如图10~图13所示。 从图10和图11中可以看到,控制系统跟踪滚转角指令准确,响应迅速,并且稳定性好;控制系统对飞行器滚转产生的侧滑角的抑制效果明显,最大侧滑角βmax=0.75°,满足小于3° 的通常设计要求。图12显示,根据反馈线性化方法设计的控制器实现了滚转通道和偏航通道的解耦控制,并且控制器能够使副翼和控制力矩陀螺协调动作,飞行器在操纵副翼跟踪滚转指令的同时,控制力矩陀螺的操纵律能够对侧滑角进行有效的抑制,避免了运动耦合的发生,最终使飞行器达到协调转弯的目的。控制过程中副翼偏角|δx|<15°,框架角|δc|<40° 均在约束范围内。通过图13的对比可以看出,基于控制力矩陀螺的侧滑角抑制装置只需要较小的输入力矩,便可获得很大的输出力矩,因此控制效率很高。综合考虑可靠性、质量、功耗和成本等因素,控制力矩陀螺是一种很有前景的新型飞行器侧滑角抑制执行机构。在后续的研究中,将通过实验的方法作进一步的验证。 图10 滚转角的时间历程曲线Fig.10 History of roll angle 图11 侧滑角的抑制效果Fig.11 Results of sideslip angle suppression 图12 执行机构操纵律Fig.12 Control law of actuator 图13 单框控制力矩陀螺的力矩放大结果Fig.13 Torgue amplification results of SGCMG 本文旨在将SGCMG应用于BTT飞行器协调转弯控制系统中,建立了SGCMG与BTT飞行器联合的倾斜转弯动力学模型,设计了基于非线性反馈和LQR算法的解耦综合控制器。从理论上证明了这种控制方法的先进性,数值仿真的结果进一步验证了所提方法的有效性。研究结果表明: 1) 基于单框控制力矩陀螺的BTT飞行器侧滑角抑制执行机构,采用两个转向相反的陀螺转子构成侧滑角抑制装置,能够对侧滑角进行有效的调节。 2) 采用控制力矩陀螺的侧滑角抑制执行机构,充分发挥了控制力矩陀螺的优点,利用较小的输入力矩可产生放大的输出力矩,力矩放大倍数可达约3.5倍并且可调,控制效率很高。 3) 根据反馈线性化方法设计的控制器,实现了飞行器滚转通道和偏航通道的解耦控制,控制器对指令信号跟踪准确,并且跟踪响应快、稳定性好。 4) 控制系统保证了副翼和控制力矩陀螺协调动作,能够完成BTT飞行器的协调转弯任务,满足飞行器横侧向机动的要求。 [1] 高清, 赵俊波, 李潜. 类HTV-2横侧向稳定性研究[J]. 宇航学报, 2014, 35(6): 657-662. GAO Q, ZHAO J B, LI Q. Study on lateral-directional stability of HTV-2 like configuration[J]. Journal of Astronautics, 2014, 35(6): 657-662 (in Chinese). [2] MENON P K, SWERIDUK G D, OHLMEYER E J, et al. Integrated guidance and control of moving-mass actuated kinetic warheads[J]. Journal of Guidance Control & Dynamics, 2002, 27(1): 118-126. [3] WOOD W, KLEB W, HYATT A. Assessment of turbulent CFD against STS-128 hypersonic flight data[C]//AIAA/ASME Joint Thermophysics and Heat Transfer Conference, 2010. [4] INNOCENTI M, THUKRAL A. Simultaneous reaction jet and aerodynamic control of missile systems[C]//AIAA Guidance, Navigation and Control Conference. Reston, VA: AIAA, 1993: 811-820. [5] RUI H, SATO K, MANABE S. Autopilot design for a missile with reaction-jet using coefficient diagram method[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston, VA: AIAA, 2001. [6] 高长生, 李君龙, 荆武兴, 等. 导弹质量矩控制技术发展综述[J]. 宇航学报, 2010, 31(2): 307-314. GAO C H, LI J L, JING W X, et al. Key technique and development for moving mass actuated kinetic missile[J]. Journal of Astronautics, 2010, 31(2): 307-314 (in Chinese). [7] ROGERS J, COSTELLO M. Control authority of a projectile equipped with a controllable internal translating mass[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1323-1333. [8] HIGUCHI T, UENO S, OHMURA T. Singularity avoidance steering logic for SGCMG systems using state feedback[C]//AIAA/AAS Astrodynamics Specialist Conference. Reston, VA: AIAA, 2010. [9] 王振, 吴忠, 蒋方超. 基于复合执行机构的再入弹头动力学建模与控制[J]. 弹道学报, 2012, 24(4): 6-10. WANG Z, WU Z, JIANG F C. Dynamic modeling and control of reentry warhead with hybrid actuators[J]. Journal of Ballistics, 2012, 24(4): 6-10 (in Chinese). [10] 吴忠, 朱挺, 魏孔明. 基于控制力矩陀螺的再入弹头姿态控制技术研究[C]//中国控制会议, 2010. WU Z, ZHU T, WEI K M. On attitude control technology of reentry warhead using control moment gyroscopes[C]//Proceedings of the 29th Chinese Control Conference, 2010 (in Chinese). [11] 张靖男, 赵兴锋, 郑志强. BTT导弹的发展现状与趋势[J]. 飞航导弹, 2006(10): 37-39. ZHANG J N, ZHAO X F, ZHENG Z Q. Development status and trend of BTT missile[J]. Aerodynamic Missile Journal, 2006(10): 37-39 (in Chinese). [12] 安相宇, 王小虎. 高超声速滑翔飞行器动态逆解耦跟踪控制方法研究[J]. 系统仿真学报, 2010, 22(s1): 107-110. AN X Y, WANG X H. Research of dynamic inversion decoupling tracking control method for hypersonic sliding vehicle[J]. Journal of System Simulation, 2010, 22(s1): 107-110 (in Chinese). [13] 王鹏. 高超声速巡航飞行器姿态控制方法研究[D]. 长沙: 国防科学技术大学, 2013. WANG P. Research on attitude control method for hypersonic cruise vehicle[D]. Changsha: National University of Defence Technology, 2013 (in Chinese). [14] ISIDORI A. 非线性控制系统[M]. 第3版. 王奔, 张圣贤, 译. 北京: 电子工业出版社, 2012: 173-183. ISIDORI A. Nonlinear control systems[M]. 3rd ed. WANG B, ZHANG S X, translated. Beijing: Electronic Industry Press, 2012: 173-183 (in Chinese). [15] 黄圳圭. 航天器姿态动力学[M]. 长沙: 国防科技大学出版社, 1997: 197. HUANG Z G. Spacecraft attitude dynamics[M]. Changsha: National University of Defence Technology Press, 1997: 197 (in Chinese). [16] 陈少楠. 船舶陀螺减摇装置设计及控制研究[D]. 青岛: 中国海洋大学, 2012. CHEN S N. Anti-roll gyro stabilizer design and control for ships[D]. Qingdao: Ocean University of China, 2012 (in Chinese). [17] 胡耀坤. 制导炸弹倾斜转弯飞行控制系统设计与仿真研究[D]. 南京: 南京理工大学, 2009. HU Y K. Design and simulation of the bank-to-turn flight control system for guided bombs[D]. Nanjing: Nanjing University of Science and Technology, 2009 (in Chinese). [18] 孙浩, 罗建军, 马卫华. 高超声速滑翔飞行器不确定性分析与H∞混合灵敏度控制[J]. 系统工程与电子技术, 2014, 36(12): 2466-2472. SUN H, LUO J J, MA W H. Uncertainty analysis andH∞mixed sensitivity control for hypersonic gliding vehicle[J]. Systems Engineering and Electronics, 2014, 36(12): 2466-2472 (in Chinese). [19] 张友安, 杨旭. BTT导弹的神经网络自适应反馈线性化控制[J]. 航空学报, 2000, 21(1): 84-86. ZHANG Y A, YANG X. Neural networks based adaptive feedback linearization for bank-to-turn missile control[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(1): 84-86 (in Chinese). [20] DA COSTA R R, CHU Q P, MULDER J A. Reentry flight controller design using nonlinear dynamic inversion[J]. Journal of Spacecraft and Rockets, 2003, 40(1): 64-71. [21] KAWAGUCHI J, MIYAZAWA Y, NINOMIYA T. Stochastic evaluation and optimization of the hierarchy-structured dynamic inversion flight control[C]//Proceedings of AIAA Guidance, Navigation and Control Conference. Reston, VA: AIAA, 2009: 1-18. [22] 李惠峰. 高超声速飞行器制导与控制技术[M]. 北京: 中国宇航出版社, 2012. LI H F. Hypersonic vehicle guidance and control technology[M]. Beijing: China Astronatuic Publishing House, 2012 (in Chinese). (责任编辑: 苏磊) *Corresponding author. E-mail: dqcao@hit.edu.cn Coordinated turn of BTT vehicle based on control moment gyroscopes ZHAO Kun, CAO Dengqing*, HUANG Wenhu SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001,China A coordinated turn control approach that takes coupling factors between channels into account is proposed for the problem on the sideslip angle introduced by the lateral maneuvering of the Bank-To-Turn (BTT) vehicle. A suppression actuator for the sideslip angle based on the Single Gimbal Control Moment Gyroscope (SGCMG) is put forward to replace traditional actuators, such as rudder, vector thrust engine, etc. A multivariable and strong coupling nonlinear BTT dynamical model is established for the case of lateral maneuvering of the BTT vehicle installed with a control moment gyroscope. According to the requirement of coordinated turning of BTT vehicle in lateral maneuvering, a decoupling control law based on feedback linearization and linear quadratic optimal algorithm is developed. Numerical results show that the coordinated turn control law is valid for tracking of the roll angle and active suppressing of the sideslip angle. Bank-To-Turn (BTT) vehicle; coordinate turn; control moment gyroscope; sideslip angle suppression; feedback non-linearization; linear quadratic regulator 2017-01-03; Revised: 2017-02-20; Accepted: 2017-04-16; Published online: 2017-05-08 16:46 URL: www.cnki.net/kcms/detail/11.1929.V.20170508.1646.002.html National Natural Science Foundation of China (91216106) V249.1 A 1000-6893(2017)09-321096-11 2017-01-03; 退修日期: 2017-02-20; 录用日期: 2017-04-16; 网络出版时间: 2017-05-08 16:46 www.cnki.net/kcms/detail/11.1929.V.20170508.1646.002.html 国家自然科学基金(91216106) *通讯作者.E-mail: dqcao@hit.edu.cn 赵坤, 曹登庆, 黄文虎. 基于控制力矩陀螺的BTT飞行器协调转弯[J]. 航空学报, 2017, 38(9): 321096. ZHAO K, CAO D Q, HUANG W H. Coordinated turn of BTT vehicle based on control moment gyroscopes[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 321096. http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn 10.7527/S1000-6893.2017.321096
3.2 线性二次最优控制算法的设计


4 仿真结果及分析











5 结 论
