高超声速可变形双翼气动特性

刘姝含， 朱战霞,*

1.西北工业大学 航天学院， 西安 710072 2.航天飞行动力学技术国家级重点实验室， 西安 710072

高超声速可变形双翼气动特性

刘姝含1,2， 朱战霞1,2,*

1.西北工业大学 航天学院， 西安 710072 2.航天飞行动力学技术国家级重点实验室， 西安 710072

为研究高超声速可变形双翼在不同迎角和不同马赫数条件下的气动特性,并针对在给定的迎角和马赫数条件下可变形双翼的舵面偏转角选取困难的问题，通过结合二分法、遗传算法和高斯牛顿算法对处于不同迎角和不同马赫数条件下的可变形双翼的舵面偏转角进行了选取确定,分析了可变形双翼的气动特性和舵面偏转角对其气动特性产生影响的机理。研究表明：当来流马赫数为5，迎角从1°～8° 变化时，可变形双翼的升阻比明显大于Busemann双翼的升阻比，最大可达4.2倍；当迎角为3°，来流马赫数从0.5～5变化时，可变形双翼的升阻比最大可达Busemann双翼升阻比的3.4倍。结果表明可变形双翼在大迎角和大速度范围内均能保持高升阻比，在高超声速飞行中将具有更好的应用价值和前景。

高超声速; 可变形双翼; 舵面偏转角; 升阻比; 迎角; 马赫数

升阻比常用于评价飞行器的气动效率，如何减小超声速飞行器的激波阻力提高其升阻比一直是各国研究人员的关注焦点。随着飞行器飞行马赫数的不断提高，如何减小高超声速飞行器在飞行过程中产生的强激波阻力，提高其气动效率也得到了越来越多的关注[1]。

Busemann为减小超声速飞行器的激波阻力提出Busemann双翼的概念并分析了其工作原理[2-3]，图1所示为Busemann双翼波系,Ma∞为来流马赫数。为解决Busemann双翼升力不足的问题，Licher在对称的Busemann双翼的基础上，提出了非对称的Licher双翼的概念[4]。两种双翼均通过激波减弱效应削弱激波，同时通过双翼间的激波和膨胀波相互干涉进一步削弱激波强度，达到减阻的目的[5]。但两种双翼在非设计工作状态下，均容易出现流动壅塞现象，使其阻力迅速增加，导致气动性能迅速下降。因此Busemann双翼和Licher双翼的研究一度陷入低谷。

近年来，由于Busemann双翼和Licher双翼在设计工作状态下显著的减阻效应，这两种双翼再次受到广泛关注。Patidar[6]和Yamashita[7]等分别使用数值模拟和风洞试验方法研究了Busemann双翼的气动特性，国内外学者还利用Buse-mann双翼对三维机翼[8-9]和飞行器的气动布局形式进行了研究[5,10-13]。

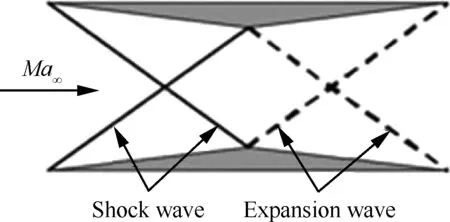
图1 Busemann双翼波系Fig.1 Wave system of Busemann biplane

针对Busemann双翼的流动壅塞问题,为进一步减小双翼的阻力，Hu等[14-15]使用伴随方法对超声速双翼进行优化，取得了较好的优化结果。日本Kusunose教授团队[6,16-19]和国内赵承熙等[20]使用反设计方法对Licher翼型进行优化，进一步减小了翼型的激波阻力[6,17-21]，但仍难以完全克服流动壅塞问题，同时反设计方法也存在难以给定合理的目标压力分布的问题。Tian和Agarwal[21]使用遗传算法对Busemann双翼进行了优化，减小了Busemann双翼的阻力，提高了升阻比。

为减小双翼在非设计工作状态下的阻力，克服流动壅塞问题，Kusunose教授团队设计出带有4个舵面的超声速可变形双翼翼型，通过改变舵面偏转角的方式，使得该翼型在宽马赫数范围内均能保持较高的升阻比[18]，可变形双翼外形如图2 所示，c为翼型弦长。但其并未研究在给定的迎角和马赫数条件下，可变形双翼舵面偏转角如何选取的问题。同时，也未对处于非零迎角下的可变形双翼在不同马赫数条件下的气动特性进行研究。而在实际飞行中，飞行器常在不同迎角和不同马赫数的条件下飞行，因此有必要对在不同迎角和马赫数条件下的可变形双翼的气动特性进行研究。

本文根据文献[18]的理念，设计一种高超声速可变形双翼。针对文献[18]未给出舵面偏转角选取方法的问题，本文结合二分法、遗传算法和高斯牛顿法对高超声速可变形双翼的舵面偏转角进行选取，解决在不同迎角和马赫数条件下，可变形双翼舵面偏转角选取困难的问题。对处于不同迎角和不同马赫数条件下的可变形双翼，分别选取相应的舵面偏转角，研究可变形双翼在大迎角范围和大马赫数范围内的气动特性，并对可变形双翼影响升阻比的机理进行分析，为可变形双翼在高超声速飞行中的应用提供参考。

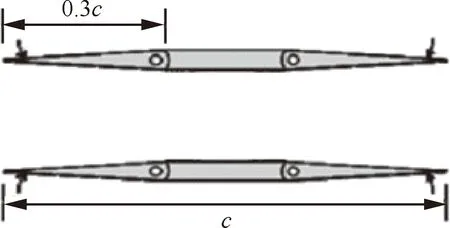
图2 可变形双翼Fig.2 Morphing biplane

1 模型建立

本文可变形双翼的设计工作状态为：来流马赫数Ma∞=5，迎角为α=0°。双翼的示意图如图3 所示，βi(i=1,2，3，4)为舵面偏转角，θi(i=1,2,…,8)为可变形双翼的几何参数，取θi=3°(i=1,2,…,8)；h为可变形双翼7边和15边的间距，取h=146.8 mm；L为双翼11边的长度，取L=100 mm。

由于θi(i=1,2,…,8)为双翼的外形参数，所以在双翼翼型设计完成后，θi(i=1,2,…,8)将不再变化；当双翼处于一个给定的工况时，迎角α同样不发生变化。因此，升阻比K只由4个变量决定，即由βi(i=1,2,3,4)决定。

设置可变形双翼的流场长度为可变形双翼弦长的60倍，流场宽度为双翼厚度的40倍。对流场进行非结构网格划分，得到274万网格，网格质量最小值为0.64，最大值为0.999 5，平均值为0.995。网格局部如图4所示。

设置可变形双翼仿真条件为：高度为30 km，来流马赫数Ma∞=5，双翼表面为壁面，计算域表面为压力远场。由于高度为30 km，空气稀薄且为高超声速飞行，因此采用无黏模型和基于密度的求解方法，压力、动量和能量方程运用二阶迎风格式，时间项的处理使用一阶隐式格式。

图3 可变形双翼示意图Fig.3 Schematic diagram of morphing biplane

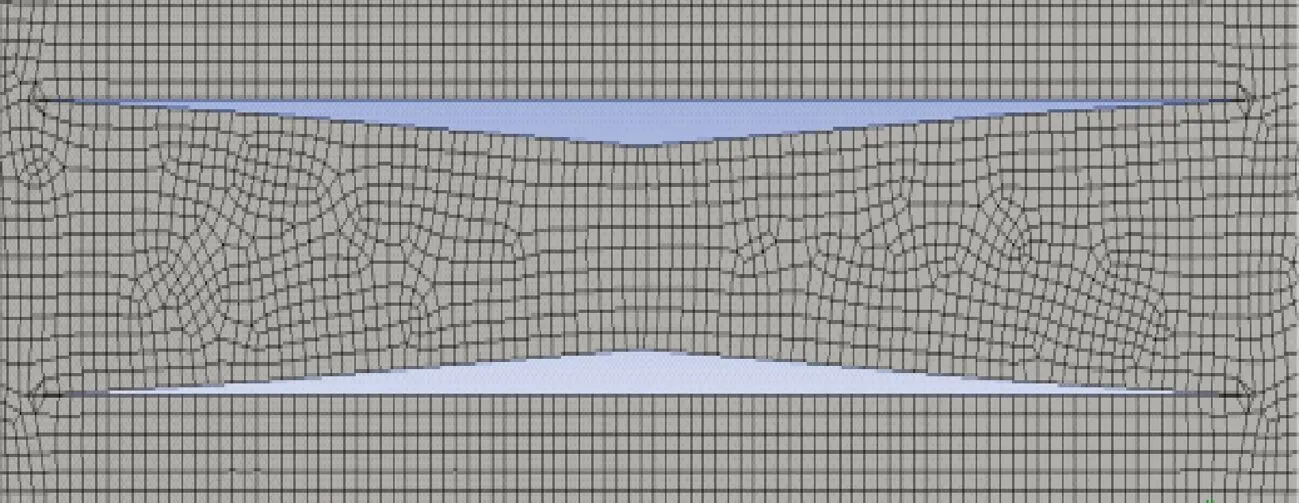
图4 可变形双翼流场局部网格Fig.4 Local mesh of flow field on morphing biplane

2 舵面偏转角

2.1 舵面偏转角的选取算法

图5为舵面偏转角选取算法的流程图，整个算法流程可分为3个部分,如3个红色方框所示。方框1表示使用二分法缩小βi(i=1,2,3,4)的取值范围，方框2表示使用遗传算法对舵面偏转角进行全局范围内的选取，方框3表示使用高斯牛顿算法在局部范围内进一步进行选取。

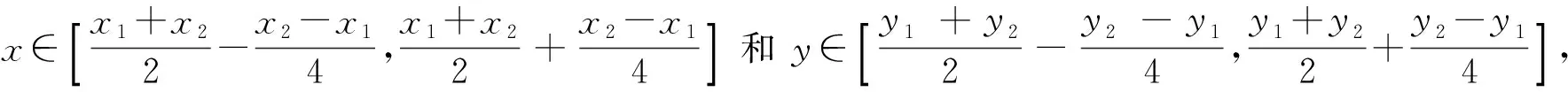
肝衰竭不是一个独立的临床诊断，而是一种功能判断。在临床实际应用中，完整的诊断应包括病因、临床类型及分期，建议按照以下格式书写：

图5 舵面偏转角选取算法流程图 Fig.5 An algorithm framework for solving deflectionangle of rudder

从图6中可以发现，目标点为正方形中心点时，一次迭代可以将求解域缩小为原求解域的1/4；目标点为正方形边上中心点时，一次迭代可以将求解域缩小为原求解域的1/8；而如果目标点为正方形顶点时，一次迭代可以将求解域缩小为原求解域的1/16。因此经过n次该算法迭代优化后,状态点个数为(32-1)n+1，最差可以将求解域缩小为原求解域的1/4n，最好可以将求解域缩小为原求解域的1/16n。

对于本文有4个变量βi(i=1,2,3,4)的情况，经过n次该算法迭代优化后，状态点个数为(34-1)n+1，最差可以将求解域缩小为原求解域的1/16n，最好可以将求解域缩小为原求解域的1/256n。可见该算法可以有效缩小求解域的范围。

使用二分法缩小参数的取值范围后，在小参数范围内建立代理模型，这时的代理模型将更为精确。利用遗传算法全局搜索能力强的特点，在缩小的参数取值范围内搜索最优解。获得最优解后，再利用高斯牛顿法局部搜索能力强的特点进行局部搜索，以获得最终的最优解。结合遗传算法和高斯牛顿法寻优，避免了遗传算法局部搜索能力不佳[22-24]和高斯牛顿法对初始值要求严格的缺点[25-26]，同时结合了两种算法的优点，使得优化结果更为精确。

图6 二分法缩小变量取值范围示意图 Fig.6 Sketch diagram of dichotomy narrow scope of a variable

本文选取舵面偏转角的3个环节中，遗传算法用于在全局范围内搜索可行解作为高斯牛顿法的初始值，目的在于防止在求解域内目标函数具有多极值从而导致高斯牛顿法局部收敛而不能取得较好的求解结果。当求解域内的目标函数明确不具有多极值时，可将使用遗传算法在全局范围内搜索可行解的环节省去，从而直接使用高斯牛顿法进行求解。

2.2 舵面偏转角取值范围的确定

为了分析舵面偏转角β1～β4对双翼升阻比的影响，本文设计出一系列状态点，探索其解空间，计算条件为：自由来流马赫数为5，迎角为3°，高度为30 km。将舵面偏转角两两组合，得到偏转不同舵面时升阻比K的6个响应曲面，如图7所示。

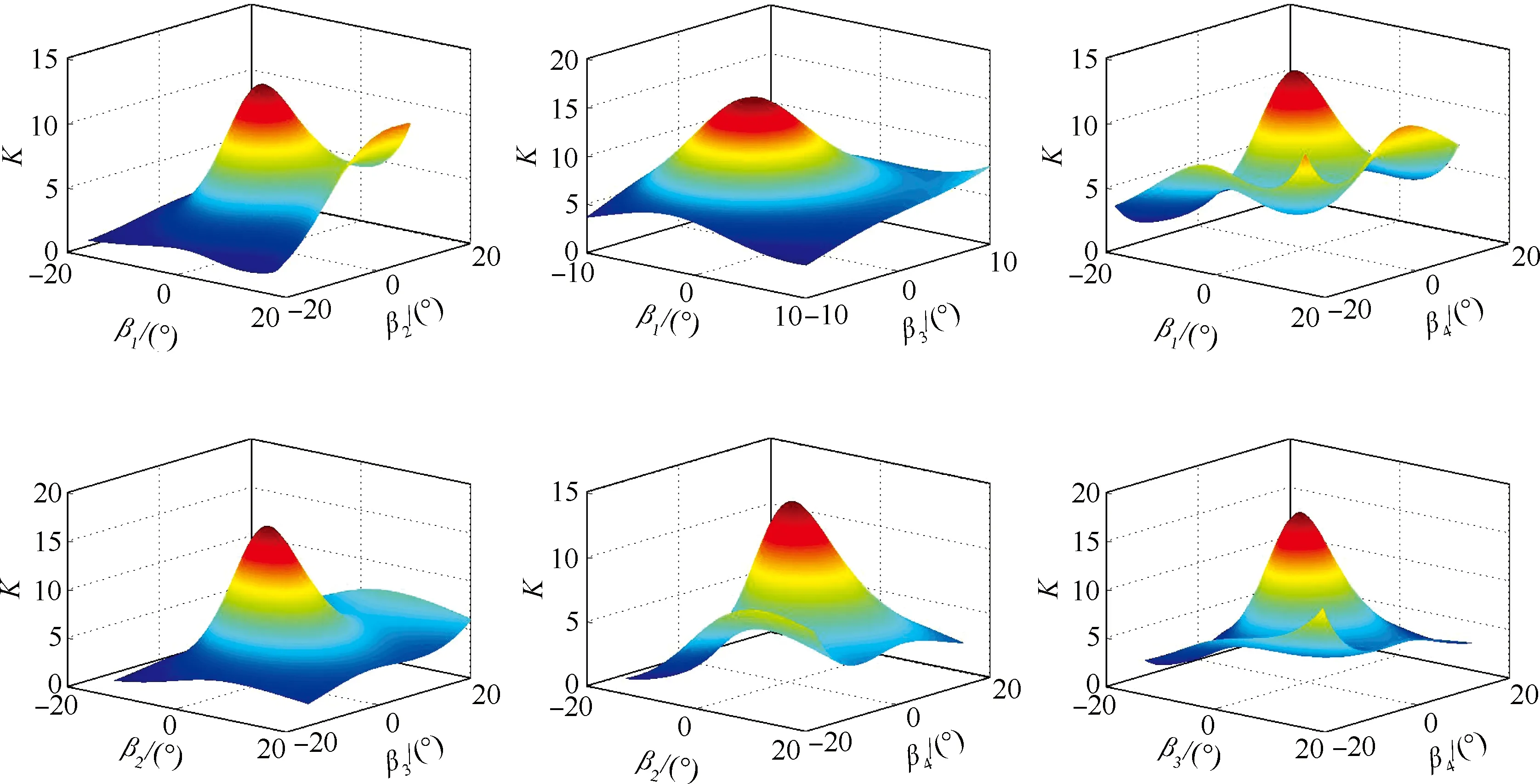
图7 升阻比随舵面偏转角变化的响应曲面Fig.7 Response surface of change of lift-drag ratio with deflection angle of rudder

图7表明不同的舵面进行组合偏转时，升阻比均存在一个峰值，在偏离这一峰值时，升阻比迅速下降；任意两个舵面偏转角进行组合，舵面偏转角的取值在[-10°,10°]范围内时，升阻比可以取得最大值。因此将βi∈[-10°,10°](i=1,2,3,4)作为优化过程中舵面偏转角的限制条件。

此时，从图7中可见，升阻比随舵面偏转角的变化均只有一个极值，但由于图7中的每一个响应面仅表示升阻比随两个舵面偏转时的响应，且每个响应面取得极值时，含有相同舵面的舵面偏转角并不相同(图7前3个图中均含有舵面偏转角β1，但升阻比取得极值时的β1并不相同)，而实际选取舵面时将同时偏转4个舵面，此时需要把舵面偏转角对升阻比的影响效应进行叠加，因此升阻比对舵面偏转角的响应具有多极值性，故本文不省去遗传算法搜索可行解的环节，以保证结果的可靠性。

2.3 算法验证

K=f(β1,β2,β3,β4)

(1)

约束条件：

(2)

式中：f(β1,β2,β3,β4)为由本文选取舵面偏转角的方法确定的升阻比K的代理模型函数。

图8显示在遗传迭代到第37代时，个体的适应度趋于稳定，优化过程终止，结果如表1所示。

将优化得到的舵面偏转角β1～β4作为高斯牛顿法的初始值，进行进一步的优化，迭代18步后，算法结束，此时结果如图9和表2所示。

图8 升阻比随遗传代数的收敛性Fig.8 Convergence of lift-drag ratio with genetic algebra

表1 遗传算法选取得到的舵面偏转角

Table 1 Selected deflection angle of rudder by genetic algorithm (°)

图9 高斯牛顿法收敛性Fig.9 Convergence of Gauss-Newton method

表2 高斯牛顿法选取得到的舵面偏转角

Table 2 Selected deflection angle of rudder by Gauss-Newton method (°)

将选取得到的舵面偏转角作为输入条件，使双翼的舵面偏转至相应的角度，设置流场计算条件和参数后，计算得到可变形双翼的流场压力分布如图10所示，计算结果如表3所示。

图10 可变形优化双翼的流场压力分布 Fig.10 Pressure distribution of flow field of optimized morphing biplane

表3 CFD验证优化结果Table 3 Optimization results verified by CFD

MethodCL/10-2CD/10-3KSurrogatemodel4.8892.59218.86CFD4.8782.58218.89

表3表明使用算法模型计算得到的升、阻力系数与由CFD计算得到的升、阻力系数相差不大，算法模型计算得到的升力系数仅比CFD计算值增大0.22%，阻力系数仅增大0.40%，升阻比减小0.16%。可见使用算法模型计算得到的升、阻力系数具有很高的计算精度。

3 计算结果与分析

3.1 不同迎角条件下可变形双翼的气动特性

飞行器在实际飞行过程中，迎角会发生变化，因此有必要研究在不同迎角条件下，可变形双翼和Busemann双翼的升阻比特性。设置仿真条件为：来流马赫数为5，迎角α在1°～8° 范围内变化。此时，使用本文选取可变形双翼舵面偏转角的算法选取得到可变形双翼在不同迎角条件下的舵面偏转角如图11(a)所示，Busemann双翼和可变形双翼的升阻比的变化情况如图11(b)所示。

图11(a)表明，随着迎角的增加，β1和β3逆时针偏转，β2和β4顺时针偏转，但偏转角的大小并不随着迎角的增大而单调变化，这也体现了选取确定舵面偏转角以使可变形双翼具有高升阻比的困难性。

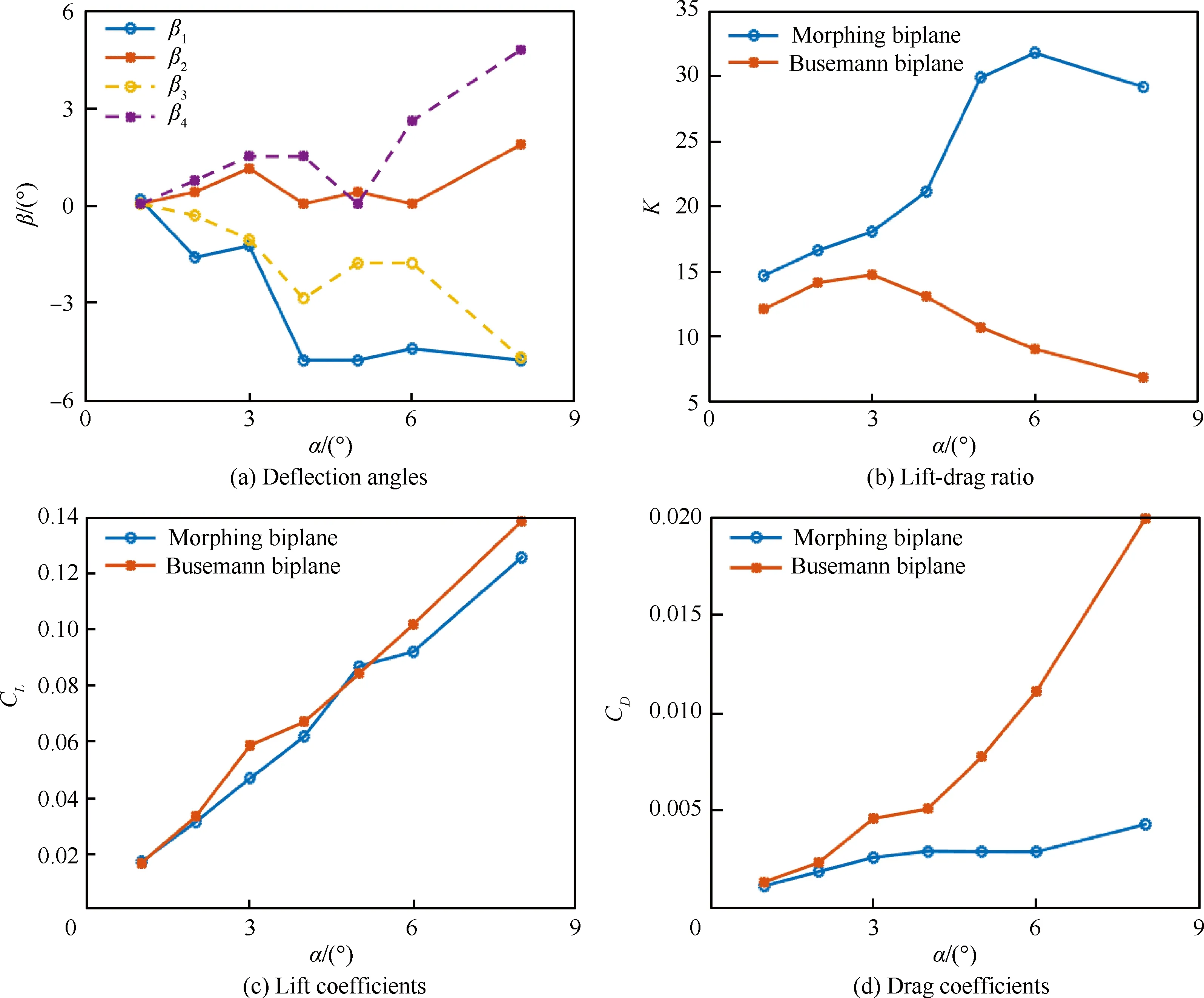
图11 不同迎角下的气动特性Fig.11 Aerodynamic characteristics with different angles of attack

图11(b)表明，随着迎角的增加，Busemann双翼和可变形双翼的升阻比均先增加再逐渐减小。Busemann双翼的最大升阻比出现在3° 迎角附近，而可变形双翼的最大升阻比出现在6° 迎角附近。对比图11(c)和图11(d)，可见随着迎角增加，可变形双翼通过偏转舵面，使得可变形双翼的升力系数虽略有减小，但同时大幅度减小了阻力系数，特别是在大迎角时，阻力系数减小明显。在迎角为8° 时，可变形双翼的阻力系数仅为Busemann双翼阻力系数的21.6%，因而使得可变形双翼升阻比的峰值出现位置推后。

为分析在不同迎角条件下可变形双翼提高升阻比的原理，以马赫数为5、迎角为8° 的计算结果为例对可变形双翼和Busemann双翼的压力系数进行分析对比。图12(a)和图12(b)分别是可变形双翼和Busemann双翼的流场压力图，图13(a)是可变形双翼上单翼与Busemann双翼上单翼的压力系数Cp对比图，图13(b)是可变形双翼下单翼与Busemann双翼下单翼的压力系数对比图。图中横坐标x表示压力系数测试点在弦线方向上的站位，弦线中点为零，前缘为-0.5 m，后缘为0.5 m。

图12 可变形双翼和Busemann双翼的流场压力云图(Ma=5, α=8°)Fig.12 Flow field pressure contour of morphing and Busemann biplanes (Ma=5, α=8°)

图13 上、下单翼的压力系数(Ma=5， α=8°) Fig.13 Pressure coefficients of above and below wings(Ma=5， α=8°)

从图12和图13(a)可见，相对于Busemann双翼，可变形双翼通过偏转舵面，使图3中上单翼1边和6边的压力系数绝对值减小，结果将使升力系数和阻力系数同时减小；4边和5边的压力系数绝对值增大，将使升力系数增大，阻力系数减小；2边、3边、7边和6边的压力系数基本无变化。因此，上单翼偏转舵面的效果是使阻力减小。

从图12和图13(b)可见，相对于Busemann双翼，可变形双翼通过偏转舵面，使图3中下单翼9边、14边和16边的压力系数绝对值减小，结果将使升力系数和阻力系数同时减小； 12边和13边的压力系数绝对值增大，将同时减小升力系数和阻力系数；10边、11边和15边的压力系数基本无变化。因此，下单翼偏转舵面的效果同样使阻力减小。

结合上、下单翼的减阻结果可见，可变形双翼通过偏转舵面可以有效减小阻力。由于可变形双翼和Busemann双翼上单翼的压力系数曲线围成图形的面积基本相当，所以上单翼产生的升力基本相当；而可变形双翼下单翼的压力系数曲线围成图形的面积稍小于Busemann双翼的压力系数曲线围成图形的面积，所以升力将略微减小。因此，可变形双翼的升力略小于Busemann双翼的升力。

综合上、下单翼计算结果可见，可变形双翼相比于Busemann双翼，升力有所减小，但减小的幅度小于阻力减小的幅度，因此可变形双翼的升阻比大于Busemann双翼的升阻比。

3.2 不同马赫数条件下可变形双翼的气动特性

飞行器在实际飞行过程中，速度会随着任务不同发生变化，尤其是在加速、俯冲等过程中，飞行器的速度范围跨度很大，因此有必要研究马赫数变化对Busemann双翼和可变形双翼升阻比特性的影响。本文在迎角为3° 时，研究马赫数在0.5～5范围内变化对Busemann双翼和可变形双翼升阻比的影响，此时，可变形双翼在不同马赫数条件下的舵面偏转角如图14(a)所示，升阻比结果如图14(b)所示。

图14(b)表明，Busemann双翼和可变形双翼在马赫数1.0和马赫数1.5时均出现了流动壅塞现象，对比图14(c)和图14(d)，发现可变形双翼通过偏转其舵面减弱了流动壅塞现象，使其阻力系数小于Busemann双翼的阻力系数，而升力系数基本不变，因此升阻比高于Busemann双翼的升阻比。在整个马赫数变化范围内，可变形双翼和Busemann双翼的升力系数基本相当，但可变形双翼通过调整舵面偏转角，使得其阻力系数小于Busemann双翼的阻力系数，因此其升阻比更高。

以迎角为3°、马赫数为3为例对比研究可变形双翼和Busemann双翼的压力系数，分析可变形双翼提高升阻比的原理。图15(a)和图15(b)分别为可变形双翼和Busemann双翼的流场压力图，图16(a)为可变形双翼上单翼与Busemann双翼上单翼的压力系数对比图，图16(b)为可变形双翼下单翼与Busemann双翼下单翼的压力系数对比图。

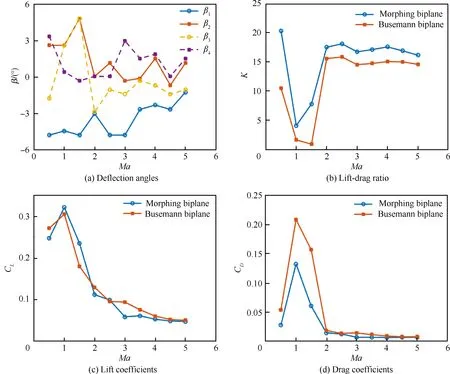
图14 不同马赫数下的气动特性Fig.14 Aerodynamic characteristics with different Mach numbers

图15 可变形双翼和Busemann双翼的流场压力云图(Ma=3, α=3°)Fig.15 Flow field pressure contour of morphing and Busemann biplanes (Ma=3, α=3°)

图16 上、下单翼的压力系数(Ma=3， α=3°)Fig.16 Pressure coefficients of above and below wings (Ma=3， α=3°)

从图15和图16(a)可见，相对于Busemann双翼，可变形双翼通过偏转舵面，使图3中上单翼2、3、7和8边的压力系数的绝对值增大，有利于增大升力系数；1边和6边的压力系数的绝对值减小，有利于减小阻力系数；4边和5边的压力系数的增幅相对较小，对增大升力系数和减小阻力系数的作用相对有限。

从图15和图16(b)可见，相对于Busemann双翼，可变形双翼通过偏转舵面，使图3中下单翼9边和14边的压力系数的绝对值减小，有利于减小阻力系数；10边和11边产生的压力系数峰值后移到了11边和12边，使原本产生的阻力变为了产生推力，从而显著减小了可变形双翼的阻力；13边和16边的压力系数相差不大，克服了Busemann双翼在此处产生的阻力；15边的压力系数基本无变化。

综合上、下单翼的计算结果，在迎角为3°、马赫数为3时，可变形双翼主要是通过偏转舵面使其升力增大、阻力减小，进而提高了升阻比。

4 结 论

1) 在不同迎角和马赫数条件下，可变形双翼舵面偏转角的选取确定既是关键点也是难点。本文结合二分法、遗传算法和高斯牛顿算法对舵面偏转角进行选取，能够以线性阶的计算量呈指数阶地缩小变量的取值范围，且最终计算得到的结果具有很高的精度。算例验证表明，使用算法模型计算得到的升力系数仅比CFD计算值大0.22%，阻力系数仅增大0.40%。

2) 可变形双翼通过偏转舵面，使激波和膨胀波充分干涉，从而大幅减小可变形双翼的阻力，同时使升力基本保持不变，因而可以在大迎角范围内大幅提高升阻比。在马赫数为5、迎角为8° 时，可变形双翼的升阻比可达Busemann双翼升阻比的4.2 倍。

3) 与Busemann双翼相比，可变形双翼可以在大马赫数范围内提高其升阻比，且可以明显减小在马赫数为1.0和1.5时流动壅塞产生的阻力。在马赫数为1.0时，阻力系数减小了36.6%，在马赫数为1.5时，阻力系数减小了61.5%。研究表明可变形双翼通过偏转舵面使其升力系数在大马赫数范围内与Busemann双翼的升力系数基本相当，同时，大幅减小了可变形双翼的阻力系数，因此可变形双翼可以在大马赫数范围内大幅提高升阻比。

相比于Busemann双翼，可变形双翼凭借其在大迎角和大马赫数范围内的优异性能，在高超声速飞行中将具有更好的实用价值和应用前景。

[1] SZIROCZAK D, SMITH H. A review of design issues specific to hypersonic flight vehicles[J]. Progress in Aerospace Sciences, 2016, 84(7): 1-28.

[2] BUSEMANN A. Aerodynamic lift at supersonic speeds[C]//The 5th Volta Aerodynamic Conference， 1935.

[3] BUSEMANN A. The relation between minimized drag and noise at supersonic speed[C]//The High-Speed Aeronautics Conference， 1955.

[4] LICHER R M. Optimum two-dimensional multiplanes in supersonic flow[C]//Douglass Aircraft Conference， 1955.

[5] 华如豪， 叶正寅. 基于Busemann双翼构型的超音速导弹减阻技术研究[J]. 应用力学学报， 2012, 29(5): 536-540.

HUA R H, YE Z Y. Drag reduction method for supersonic missile based on Busemann biplane concept[J]. Chinese Journal of Applied Mechanics, 2012, 29(5): 536-540 (in Chinese).

[6] PATIDAR V K, YADAV R, JOSHI S. Numerical investigation of the effect of stagger on the aerodynamic characteristics of a Busemann biplane[J]. Aerospace Science & Technology, 2016, 55(8): 252-263.

[7] YAMASHITA H, KURATANI N, YONEZAWA M, et al. Wind tunnel testing on start/unstart characteristics of finite supersonic biplane wing[J]. International Journal of Aerospace Engineering, 2013(6): 1-10.

[8] MARUYAMA D, MATSUSHIMA K, KUSUNOSE K, et al. Three-dimensional aerodynamic design of low-wave-drag supersonic biplane using inverse problem method[J]. Journal of Aircraft, 2015, 46(6): 1906-1918.

[9] YONEZAWA M, OBAYASHI S. Aerodynamic performance of the three-dimensional lifting supersonic biplane[J]. Journal of Aircraft, 2015, 47(3): 983-991.

[10] DAN I, ARAD E. A parametric study of an axisymetric Busemann biplane configuration[J]. Journal of Aircraft, 2013, 46(6): 1930-1937.

[11] MARUYAMA D, KUSUNOSE K, MATSUSHIMA K, et al. Aerodynamic analysis and design of Busemann biplane: Towards efficient supersonic flight[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering, 2012, 226(2): 217-238.

[12] 李占科, 张翔宇, 冯晓强, 等. 超声速双层翼翼型的阻力特性研究[J]. 应用力学学报, 2014(4): 483-488.

LI Z K, ZHANG X Y, FENG X Q, et al. The study on the drag characteristic of supersonic biplane[J]. Chinese Journal of Applied Mechanics, 2014(4): 483-488 (in Chinese).

[13] XU Y Z, XU Z Q, LI S G, et al. A hypersonic lift mechanism with decoupled lift and drag surfaces[J]. Science China: Physics, Mechanics & Astronomy, 2013, 56(5): 981-988.

[14] HU R, JAMESON A, WANG Q Q. Adjoint-based aerodynamic optimization of supersonic biplane airfoils[J]. Journal of Aircraft, 2012, 49(3): 802-814.

[15] HU R. Supersonic biplane design via adjoint method[D]. Stanford, CA: Stanford University, 2009.

[16] KUSUNOSE K. A fundamental study for the development of boomless supersonic transport aircraft[C]//The 44th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2006.

[17] MATSUSHIMA K, TAKANASHI S. An inverse design method for wings using integral equations and its recent progress[C]//Proceedings of Lectures and Workshop International Recent Advances in Multidisciplinary Technology and Modeling, 2008.

[18] KUSUNOSE K, MATSUSHIMA K, MARUYAMA D. Supersonic biplane—A review[J]. Progress in Aerospace Sciences, 2011, 47(1): 53-87.

[19] YAMASHITA H, YONEZAWA M, OBAYASHI S, et al. A study of Busemann-type biplane for avoiding choked flow[C]//The 45th AIAA Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2007.

[20] 赵承熙， 叶正寅， 华如豪. 新型目标压力分布下的Licher双翼反设计方法研究[J]. 空气动力学学报, 2015, 33(5): 610-616.

ZHAO C X， YE Z Y， HUA R H. Inverse design method for the Licher biplane with a new target pressure distributio[J]. Acta Aerodynamica Sinica, 2015, 33(5): 610-616 (in Chinese).

[21] TIAN Y, AGARWAL R K. Shape optimization of Busemann-type biplane airfoil for drag reduction under non-lifting and lifting conditions using genetic algorithms[C]//Optimization Algorithms-Methods and Applications, 2015.

[22] HUANG L, HUANG G, LEBEAU R P, et al. Optimization of aifoil flow control using a genetic algorithm with diversity control[J]. Journal of Aircraft, 2015, 44(4): 1337-1349.

[23] GURUSWAMY G. Dynamic stability analysis of hypersonic transport during reentry[J]. AIAA Journal, 2016, 54(11): 3374-3381.

[24] CROSSLEY W A, LAANANEN D H. Conceptual design of helicopters via genetic algorithm[J]. Journal of Aircraft, 2015, 33(6): 1062-1070.

[25] MINOT A, LU Y M, LI N. A distributed Gauss-Newton method for power system state estimation[J]. IEEE Transactions on Power Systems, 2015, 31(5): 3804-3815.

[26] BAO J F, LI C, SHEN W P, et al. Approximate Gauss-Newton methods for solving underdetermined nonlinear least squares problems[J]. Applied Numerical Mathematics, 2017, 111(1): 92-110.

(责任编辑： 李明敏)

URL： www.cnki.net/kcms/detail/11.1929.V.20170602.1655.008.html

*Corresponding author. E-mail: zhuzhanxia@nwpu.edu.cn

Aerodynamic characteristics of hypersonic morphing biplane

LIU Shuhan1,2, ZHU Zhanxia1,2,*

1.CollegeofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.NationalKeyLaboratoryofAerospaceFlightDynamics,Xi’an710072,China

To study the aerodynamic performance of the morphing biplane under different angles of attack and different Mach numbers, as well as the difficulty in selecting the deflection angle of rudder with given angle of attack and Mach number, this paper combines dichotomy, genetic algorithm and Gauss-Newton algorithm to determine the deflection angle of rudder of the morphing biplane under different angles of attack and different Mach numbers. The aerodynamic characteristics of the morphing biplane and the influence of the deflection angle of rudder on the aerodynamic characteristics are analyzed. It is shown that as the Mach number is 5, and the angle of attack ranges from 1° to 8°, the lift-drag ratio of the morphing biplane is obviously greater (up to 4.2 times) than that of Busemann biplane. When the angle of attack is 3°， and the Mach number ranges from 0.5 to 5, the lift-drag ratio of the morphing biplane can be up to 3.4 times than that of Busemann biplane. These results indicate that the morphing biplane can maintain a high lift-drag ratio at large angle of attack and high speed range, and has better applicability and prospects in hypersonic flight.

hypersonic; morphing biplane; deflection angle of rudder; lift-drag ratio; angle of attack; Mach number

2017-04-25； Revised： 2017-05-11； Accepted： 2017-05-31； Published online： 2017-06-02 16:55

V211.3

A

1000-6893(2017)09-121352-11

2017-04-25； 退修日期： 2017-05-11； 录用日期： 2017-05-31； 网络出版时间： 2017-06-02 16:55

www.cnki.net/kcms/detail/11.1929.V.20170602.1655.008.html

*通讯作者.E-mail: zhuzhanxia@nwpu.edu.cn

刘姝含， 朱战霞． 高超声速可变形双翼气动特性[J]． 航空学报, 2017, 38(9): 121352. LIU S H, ZHU Z X. Aerodynamic characteristics of hypersonic morphing biplane[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 121352.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121352