超临界压力低温甲烷波纹管内强化换热数值研究
2017-11-20黄世璋阮波高效伟
黄世璋, 阮波, 高效伟
大连理工大学 航空航天学院, 大连 116024
超临界压力低温甲烷波纹管内强化换热数值研究
黄世璋, 阮波, 高效伟*
大连理工大学 航空航天学院, 大连 116024
以发动机主动再生冷却系统为研究对象,建立了碳氢燃料热物性高精度计算方法,在此基础上对超临界压力下低温甲烷在水平波纹管内的流动换热现象展开数值研究,初步分析了波纹管强化换热机理。进一步系统研究了波纹管节高比、管壁材料导热系数、壁面热流密度、入口压力以及雷诺数对强化换热和阻力特性的影响,并采用综合换热性能评价准则对各种因素的影响进行评价。研究表明:在超临界压力下合理选择波纹管可以显著提升换热能力,消除传热恶化现象,并且不会带来明显的压降损失;存在一个最优波高和最佳雷诺数,使波纹管具有最优的综合换热性能;增大管壁材料导热系数和甲烷入口压力可提高换热能力。
超临界压力; 低温甲烷; 波纹管; 强化换热; 主动再生冷却
采用机载碳氢燃料作为冷却剂的主动再生冷却技术是目前最有效的冷却方式之一,在液体火箭发动机热防护中发挥着重要作用。主动再生冷却的基本原理是燃料在进入燃烧室之前,首先流经燃烧室壁内的冷却通道,将燃烧室壁面温度降低至材料允许的温度,同时将带走的热量回收至燃烧室再利用[1-2]。随着当代大型液体火箭发动机推力、比冲的不断提升,燃烧室压力和热负荷急剧增加,室壁冷却面临着更高热流的挑战,传统的冷却通道已经无法满足高效冷却的要求,需要从冷却结构和强化换热等方面采取措施来解决高压推力室高热流下的冷却问题。常用的强化换热方法有冷却通道内加肋、人工粗糙元以及球凹陷等形式[3-5]。相比之下,波纹管由于结构简单、加工技术成熟、不易结垢和堵塞及较高的综合换热性能等优点,在工业中得到广泛应用[6]。
国内外学者针对波纹管强化换热展开了多方面的研究。肖金花等[7]对水在波纹管内的流动与换热特性进行了数值模拟,结果表明波纹管能显著提高换热能力,其强化倍数达到相同条件下光滑管的1.06~3.00倍;曾敏等[8]通过实验研究了波纹管内空气强化换热及阻力特性,发现在换热强化的同时阻力系数也随之增加,但综合换热性能优于传统光滑管。Yang等[9]研究了油-水混合物在螺旋波纹管内的换热和阻力特性,结果表明,相对于光滑管道,螺旋波纹管换热系数增加了30%~120%,同时阻力系数增加了60%~160%。Vicente等[10-11]通过实验对比研究了水和乙二醇在螺旋波纹管和光滑管内的流动换热现象,研究发现强化换热带来的阻力增加在5%~20%之间,而努塞尔数在高雷诺数时可增加30%。Barba等[12]研究了中等雷诺数(100≤Re≤800)下乙二醇在波纹管内的换热和压降特性,相对于光滑管道,波纹管努塞尔数显著提升,且阻力系数仅增加1.83~2.45倍。Laohalertdecha和Wongwises[13]对R-134a制冷剂在螺旋波纹管内的流动换热和压降特性进行了实验研究,发现随着壁面热流和质量流量增加,平均换热系数和压降也逐渐增大;与光滑管道相比,换热系数和压降分别增大50%和70%。
目前有文献报道的关于波纹管强化换热研究主要集中在常压下的流动换热,对于超临界压力下强化传热性能的研究尚不多见。本文针对超临界压力下低温甲烷在水平波纹管中的流动换热现象展开数值模拟研究,重点考察波纹管节高比(Pitch-to-Height Ratio)、管壁材料导热系数、壁面热流密度、入口压力及雷诺数对综合换热性能的影响,旨在揭示超临界压力下甲烷在波纹管内流动换热特性和规律,考察波纹管强化换热效果,为主动再生冷却通道强化换热设计和优化提供参考。
1 物理模型与计算方法
本文计算模型如图1所示,其中x、r分别表示管道轴向和径向。管道内径为2 mm,外径为3 mm,总长800 mm,加热段总长500 mm。入口处给定甲烷压力p0、速度u0、温度T0,加热段外壁面施加均匀热流密度qw。波纹管加热段内壁面由多段凹凸的圆弧组成,其中P为波纹管的波纹节距,简称波距(Corrugation Pitch),H为波纹管的波高(Corrugation Height)。为了保证入口段边界层的充分发展并减少出口边界条件对计算结果的影响,管道前后各有150 mm的光滑壁面绝热段。计算中同时考虑了甲烷与壁面耦合传热,并与相同工况下光滑壁面水平圆管内的流动换热能力进行对比。本文所有算例Gr/Re2的最大值约为10-4量级,可忽略浮升力的影响,故可采用轴对称模型计算。
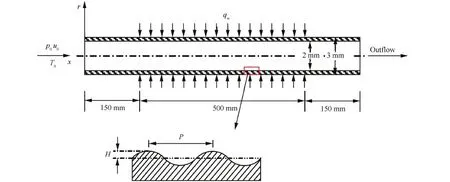
图1 波纹管物理模型示意图 Fig.1 Schematic diagram of a corrugated tube physical model
1.1 控制方程
本文求解的为流固耦合传热问题,包含固体域中的热传导过程和固体域与流体域之间的对流传热过程。在流体区域求解连续性方程、动量方程、能量方程以及标准k-ε湍流控制方程:
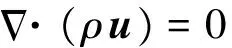
(1)
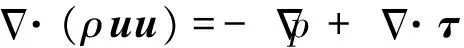
(2)
(3)
(4)
(5)
式中:ρ为密度;u为速度;p为压强;τ为黏性应力张量;et为流体总内能;λ为导热系数;T为温度;k为湍动能;μ为黏性系数;μt为湍流黏性系数;ε为耗散率;Gk为湍流生成项;σε为k-ε方程普朗特数;C1、C2为常数,分别为1.44和1.92。
为准确捕捉近壁面参数变化,采用了强化壁面处理,当网格处于近壁面时采用适用于低雷诺数的一方程Wolfstein 湍流模型,否则使用壁面函数计算。
在固体区域,计算固体热传导方程:
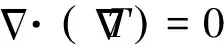
(6)
分别在流体域和固体域中求解上述方程,在流固交界面上满足温度和热流密度协调条件。
1.2 物性计算
超临界流体的物性参数受多种因素的影响,部分参数在临界点附近变化非常剧烈,以至流动的轻微变化也会对传热产生显著影响,甚至引起传热恶化,所以物性计算精度直接决定着流动传热计算结果的可信度。
为提高物性的计算精度,本文采用Helmholtz自由能状态方程[14]。Helmholtz自由能状态方程因形式简单,计算精度高,被广泛应用于碳氢燃料热物性计算[15-16]。本文通过各物性参数与Helmholtz自由能之间的关系,采用高精度Helmholtz自由能状态方程计算密度、比热等物性参数。状态方程形式为
Ar(ρ,T)/RT=(A(ρ,T)-Aid(ρ,T))/RT
(7)
式中:A(ρ,T)为Helmholtz自由能;Aid(ρ,T)为理想气体部分的Helmholtz自由能;Ar(ρ,T)为残余Helmholtz自由能;R为气体常数。各物性参数和Helmholtz自由能的关系式详见文献[15]。

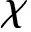
(8)
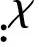
1.3 数值方法验证
首先计算了甲烷在不同压力p0下热物性随温度的变化情况,并与美国国家标准技术研究院(National Institute of Standards and Technology,NIST)的数据[20]做了比较,如图2所示。计算结果能准确描述物性在虚拟临界温度附近的变化情况,其中密度ρ和导热系数λ计算误差在2%以内,定压比热容cp计算误差在8%以内,黏性系数μ计算误差在9%以内,这表明本文采用的物性计算方法是非常准确的。
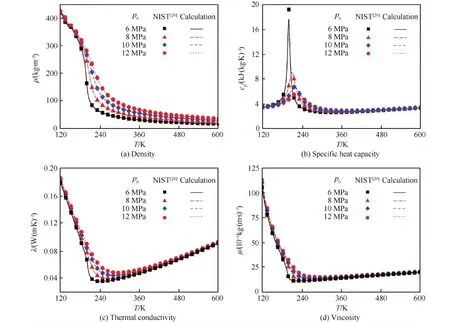
图2 甲烷热物性计算结果 Fig.2 Calculated thermophysical properties of methane
为进一步验证数值方法的可靠性,选择文献[21]中的超临界压力正癸烷竖直圆管内流动换热实验以及文献[22]中的超临界压力低温甲烷水平圆管内流动换热数值计算结果对本文方法进行验证。文献[21]中,圆管内径为2 mm,总长959 mm,加热段长为759 mm,实验中正癸烷入口雷诺数Re=7 000, 温度T0=423.15 K,压力p0=3 MPa,质量流量m=10 kg/h。由于该组实验浮升力影响可忽略,故计算中也未予考虑,并采用轴对称模型计算。图3比较了数值计算与实验测量的壁面温度Tw,可以发现各个热流密度条件下的计算结果均与实验吻合很好。文献[22]中,圆管内径为4 mm,总长1 200 mm,加热段长800 mm,入口处单位面积质量流量G=8 500 kg/(s·m-2),温度T0=118 K,压力p0=13 MPa。图4(a)和图4(b)分别为本文计算的壁面温度Tw和对流换热系数h与文献[22]计算结果的对比情况,本文数值方法可以准确地计算出传热恶化发生的位置以及壁面温度和对流换热系数的变化趋势,这进一步证明了本文物性计算方法和湍流传热数值模型是可靠的。
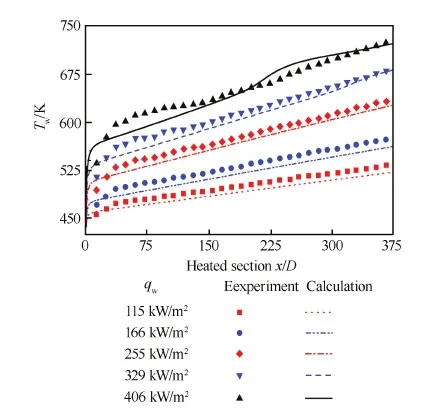
图3 计算结果与实验结果[21]对比 Fig.3 Calculational vs experimental[21] results
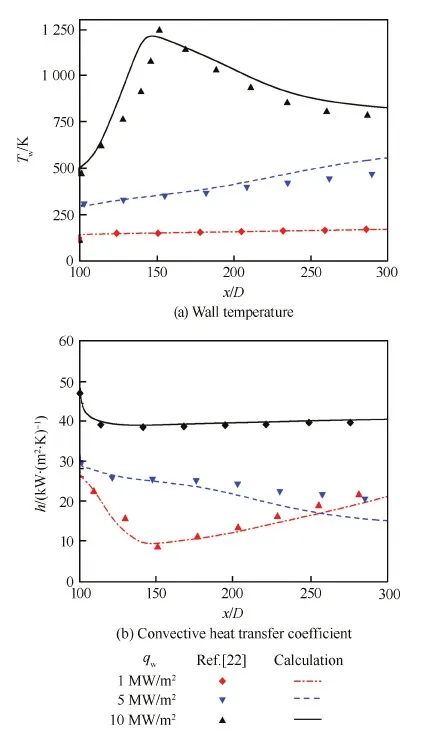
图4 与Urbano & Nasuti数值模拟结果[22]对比 Fig.4 Comparison with Urbano & Nasuti’s numerical simulation results [22]
2 结果与讨论
为了保证计算结果的可信度,在数值研究之前需要进行网格独立性分析。在入口速度为15 m/s、温度为120 K、压力为8 MPa、壁面热流为 3 MW/m2的工况下,对波距P=4 mm,波高H=0.05 mm的波纹管分别采用90×8 000、100×8 000、100×10 000(半径 × 长度方向)的3套网格进行了计算,计算得到的壁面温度和努塞尔数误差均在2%以内。为了保证计算精度最终选择了100 × 8 000的网格进行后续研究。本文网格将近壁面的前3层网格置于黏性底层(y+≤5),并且同时满足壁面第一层网格的y+≤1。因壁面函数求解超临界压力下流动传热的适用性尚不明确,这样就可以不使用壁面函数,直接求解黏性底层,保证近壁面处的计算精度。
2.1 节高比的影响
本文将波纹管波距P和波高H的比值定义为节高比R′。本节主要研究R′的变化对强化换热能力的影响。比值R′的变化通过保持波距P为4 mm不变而改变波高H得到。计算中管道入口处速度为15 m/s、温度为120 K、压力为8 MPa,管道固体壁面材料导热系数均为50 W/(m·K),加热段热流密度为一恒定值3 MW/m2,施加在管道外壁面。
本文为耦合传热问题,故引入等效换热系数[3,23]:
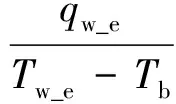
(9)
式中:qw_e为外壁面均匀热流密度;Tw_e为外壁面温度;Tb为流体平均温度,定义为
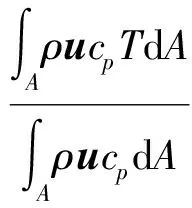
(10)
引入当地等效努塞尔数来评价当地的换热程度[3]:
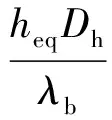
(11)
式中:Dh为水力直径;λb为平均导热系数。
图5为管道加热段外壁面温度沿流向变化情况,其中光滑管道从x=100 mm(x=0 mm表示加热段起始点)到x=200 mm之间温度急剧升高,在x=200 mm位置壁面温度达到最大值。进一步分析等效努塞尔数,如图6所示,等效努塞尔数与壁面温度发生同步变化,从x=100 mm到x=200 mm之间等效努塞尔数突然下降,并且在壁面温度达到最大值的位置等效努塞尔数也下降到最小值,说明在加热段中间出现了明显的传热恶化现象。然而对于波纹管,当节高比R′=400.0 (H=0.01 mm)时,仍出现严重的传热恶化,说明该波高的波纹管只有轻微的换热强化,强化程度几乎可以忽略不计。随着波高的增加,当R′=133.3(H=0.03 mm)时外壁面温度有所降低,虽然也出现了传热恶化,但是相对光滑管道恶化程度较轻。继续增大波高,当R′=80.0(H=0.05 mm)时,外壁面温度大幅度降低,且当地等效努塞尔数明显增大,说明此时传热恶化现象已经基本消除,冷却效果得到很大程度的改善。从图5和图7中可以明显看出随着波高增加,管壁固体区域温度持续降低,冷却效果显著增强,当R′=40.0 (H=0.10 mm)时,外壁面x=200 mm处温度较光滑管道降低约385 K。
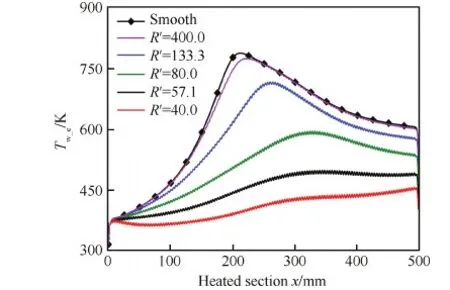
图5 不同节高比冷却通道外壁面温度变化 Fig.5 Variations of exterior surface temperature of cooling tubes with different pitch-to-height ratios
图8和图9分别为不同管道内甲烷的定压比热容和密度分布。在光滑管近壁面位置,随着甲烷的流动,在x=100 mm位置附近温度达到并超过了该压力下的虚拟临界值,此时甲烷热物性发生突变,其中定压比热容先是达到最大值然后又急剧下降,密度也出现快速下降的现象,近壁面出现大片低密度、低定压比热容的区域,但中心主流区域密度和定压比热容依然较大,沿径向出现明显的分层现象,如图8(a)和图9(a)所示。由于低密度、低定压比热容区域中单位体积热容低,这就导致换热能力严重下降。在同样的壁面热流条件下,通过图8(d)和图9(d)可以看出,对于波纹管,尤其是节高比R′=57.1时,近壁面区域和中心主流区域物性没有出现明显的分层现象,即使在近壁面区,也没有出现很低的密度和定压比热容,所以依然具有较好的换热性能。
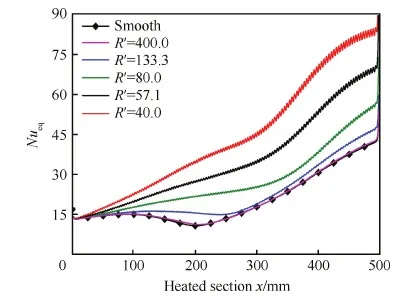
图6 不同节高比冷却通道等效努塞尔数变化 Fig.6 Variations of equivalent Nusselt number of cooling tubes with different pitch-to-height ratios
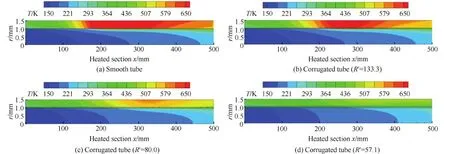
图7 冷却通道固体域和流体域温度变化 Fig.7 Variations of temperature in both solid and fluid regions of cooling tubes
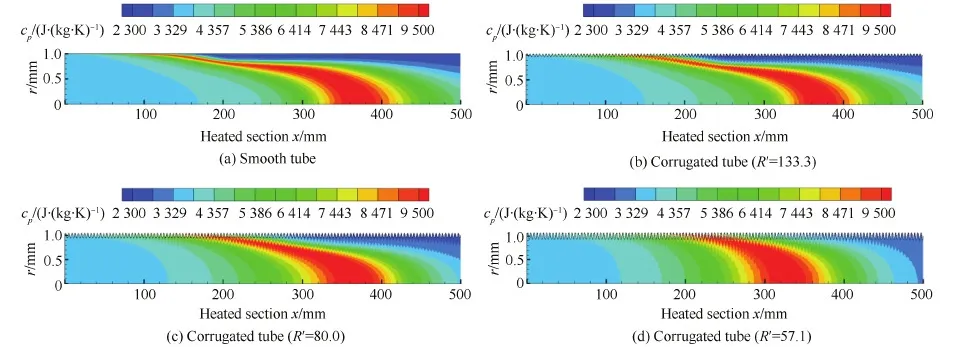
图8 比热容变化 Fig.8 Variations of specific heat capacity
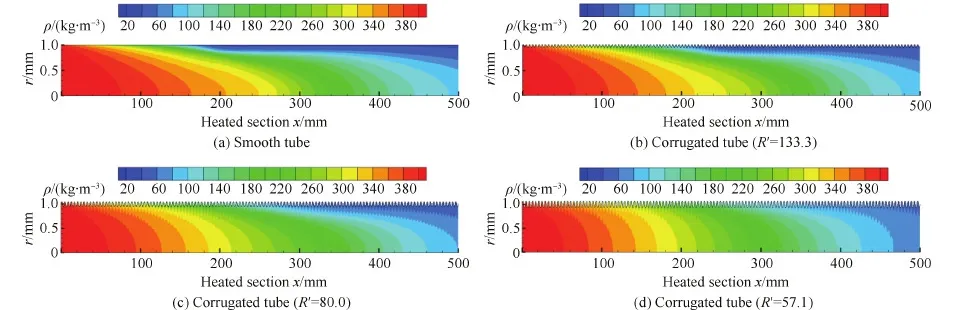
图9 密度变化 Fig.9 Variations of density
湍动能是衡量湍流强度的一个重要参数,直接关系到边界层内的动量和能量的输运过程。湍动能较强的区域,流体速度出现波动且变化剧烈,质量和能量交换的程度较大,换热强度较高。因此,从湍动能分布角度来分析流动对传热的影响,可以很好地说明换热强弱的原因[4]。
图10为光滑管和节高比R′=57.1的波纹管近壁面处湍动能(TKE)分布以及流线变化情况。当甲烷开始进入圆弧凹腔时,由于出现流动分离,湍动能开始迅速增加,圆弧凹腔底部和后缘迎风面处流体微团发生碰撞使湍动能出现峰值。通过流线分布可以发现波纹管内流动速度存在很大波动,流体的波动有利于边界层和主流区域的能量、动量交换,故而有利于增强换热。图11为不同截面径向湍动能分布,图中光滑管的高湍动能区域很薄,仅在离壁面很近的区域(r=0.9~1.0 mm),而在中心主流区域(r=0~0.9 mm)湍动能迅速降低,明显低于波纹管内相同截面位置的湍动能。在波纹管下游区域x=400 mm的截面,高湍动能流体占据了整个区域。通过分析换热能力和湍动能的分布情况,可以明显看出湍动能越高的区域换热能力也越强。由于波纹管更容易引起较高的湍动能,所以十分有利于强化换热。
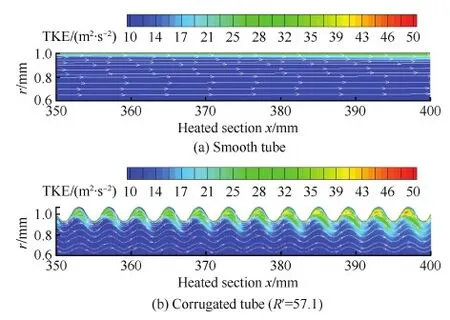
图10 光滑管和波纹管的近壁面湍动能变化 Fig.10 Variations of turbulence kinetic energy in near wall region of smooth and corrugated tubes
图12为不同管道加热段的沿程压力变化,压降越大则阻力越大,因此阻力随着波高的增加而迅速增大。图中的波纹线是计算出来的结果,表示沿着轴线方向物理量会出现抖动。
通过数值研究发现,随着换热的强化,阻力也迅速增加。在强化换热过程中,希望尽可能提高换热能力,同时也要避免流动阻力过大,因此阻力系数也是换热器设计需要考虑的另一个因素。为了综合评价换热和阻力特性,本文引入式(12)中的综合换热性能系数η评价波纹管的强化换热能力[4,24]
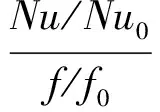
(12)
式中:η为单位阻力系数增加带来的强化换热程度。该准则同时考虑了传热的强化及随之而来的阻力增大,因此可以认为性能系数越大,则强化性能越好。平均阻力系数f的计算表达式为
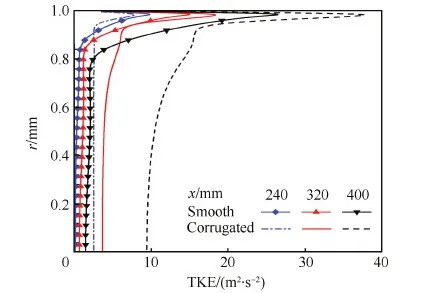
图11 光滑管和波纹管不同截面湍动能变化 Fig.11 Variations of turbulence kinetic energy in different cross-sections of smooth and corrugated tubes
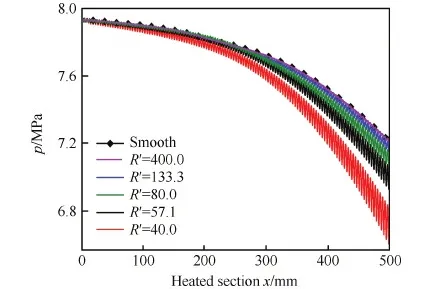
图12 不同节高比冷却通道沿程压力变化 Fig.12 Variations of pressure along cooling tubes with different pitch-to-height ratios
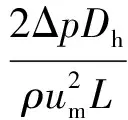
(13)
式中:Δp为加热段进出口压差;L为加热段长度;um为平均速度;通常用f/f0表示强化换热管相对于光滑管的阻力增加程度,f0为相同工况光滑圆管的平均阻力系数。为了整体评价换热性能,需要计算管道的沿程平均努塞尔数Nu,计算表达式为
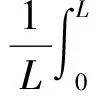
(14)
通常用Nu/Nu0表示强化换热管相对于光滑管的换热增加程度,Nu0为光滑圆管的沿程平均努塞尔数。
为了研究强化换热效果随节高比的变化规律,继续研究了波高H=0.13 mm、H=0.17 mm 的波纹管换热性能。表1列举了各种冷却通道的换热增加程度Nu/Nu0、阻力增加程度f/f0以及综合换热性能系数η。通过分析换热性能系数,发现存在一个最优高度(0.07 mm附近),此时强化换热能力最佳,性能系数达到最大。当H=0.13 mm时换热程度增加了2.63倍,阻力系数增大了2.36倍,换热增加程度依然大于阻力增加程度。当波高增大到0.17 mm时,此时阻力增加程度已经超过了强化换热的程度,所以存在一个临界高度,当波高大于此临界高度时,阻力显著增加,导致综合换热性能下降。
表1不同节高比冷却通道综合换热性能系数
Table1Overallthermalperformancefactorscalculatedforcoolingtubeswithdifferentpitch-to-heightratios
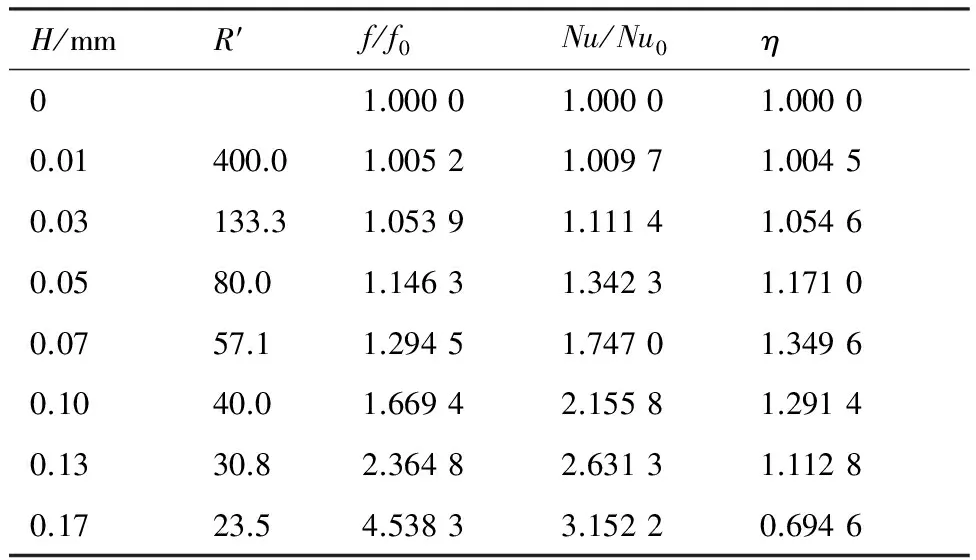
H/mmR′f/f0Nu/Nu0η01.00001.00001.00000.01400.01.00521.00971.00450.03133.31.05391.11141.05460.0580.01.14631.34231.17100.0757.11.29451.74701.34960.1040.01.66942.15581.29140.1330.82.36482.63131.11280.1723.54.53833.15220.6946
2.2 材料导热系数的影响
冷却系统需要同时承受严酷的热力载荷,对材料性能提出了苛刻的要求,其中导热系数对热量传递有重要影响。为了研究不同管壁导热系数对波纹管强化换热的影响,本节选择波高H=0.07 mm、壁面导热系数在20~200 W/(m·K)范围内的4种不同材料的波纹管进行研究。其他工况与2.1节相同。
图13和图14分别为不同导热系数冷却通道加热段外壁面温度和等效努塞尔数沿流向变化情况。对于光滑管道,当导热系数在20~200 W/(m·K)之间变化时,外壁面最高温度从842 K降低到755 K,降低了87 K,相应地,波纹管外壁面最高温度从556 K降低到466 K,降低了90 K。因此增大壁面导热系数波纹管和光滑管换热能力都有所提升。图中可以看出各种导热系数下的光滑管均出现传热恶化现象,所以增大光滑管壁面导热系数并没有消除传热恶化。然而,所有的波纹管都完全消除了传热恶化,因此在各种导热系数下波纹管均有良好的强化换热能力。
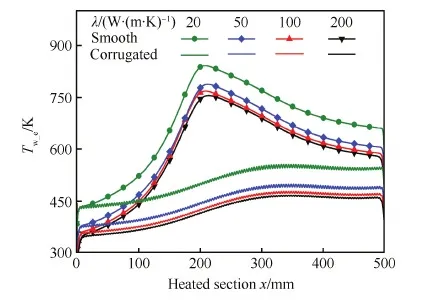
图13 不同壁面导热系数冷却通道外壁面温度变化 Fig.13 Variations of exterior surface temperature of cooling tubes with different wall thermal conductivities
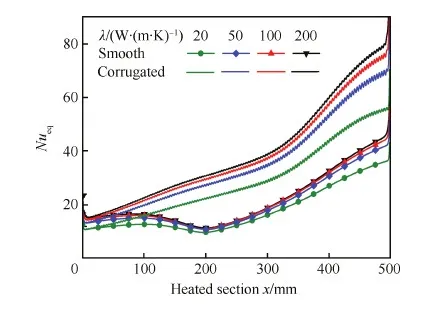
图14 不同壁面导热系数冷却通道等效努塞尔数变化 Fig.14 Variations of equivalent Nusselt number of cooling tubes with different wall thermal conductivities
图15所示为冷却通道加热段的沿程压力变化,光滑管和波纹管沿程压降几乎都不随导热系数变化,故导热系数变化对阻力的影响可忽略不计。表2为不同导热系数下波纹管的综合换热性能系数,可以看出随着导热系数增大性能系数也逐渐增大。综上所述,增大管壁的导热系数会带来换热的强化,且不会带来额外的阻力,这对于提高换热性能是非常有利的。
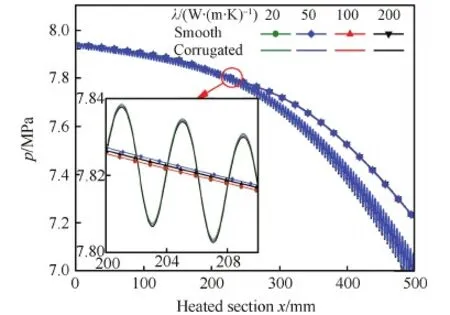
图15 不同壁面导热系数冷却通道沿程压力变化 Fig.15 Variations of pressure along cooling tubes with different wall thermal conductivities
表2 不同壁面导热系数冷却通道综合换热性能系数
Table2Overallthermalperformancefactorscalculatedforcoolingtubeswithdifferentwallthermalconductivities
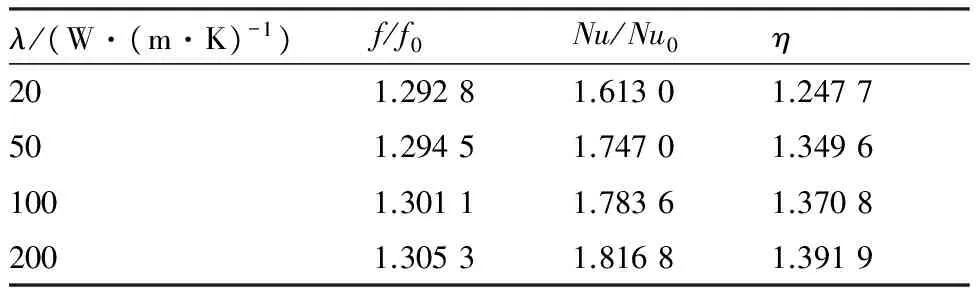
λ/(W·(m·K)-1)f/f0Nu/Nu0η201.29281.61301.2477501.29451.74701.34961001.30111.78361.37082001.30531.81681.3919
2.3 热流密度的影响
燃烧室壁面热流与发动机工作状态有关,为满足各种热流载荷下冷却通道的冷却要求,需要进一步研究壁面热流对波纹管强化换热能力的影响。本节选择不同壁面热流对波高H=0.07 mm的波纹管进行研究,其他工况与2.1节相同。
图16和图17分别为不同热流密度下冷却通道加热段外壁面温度和等效努塞尔数沿流向变化情况。当热流密度为2 MW/m2时,光滑管和波纹管均未出现传热恶化,但是波纹管有更好的冷却效果,外壁面温度大幅度降低。当热流密度增大到3 MW/m2时,光滑管出现了明显的传热恶化,在x=200 mm处恶化程度最为严重,然而该热流密度下波纹管可完全消除传热恶化,在x=200 mm处外壁面温度比光滑管降低约340 K。当壁面热流增大到5 MW/m2时光滑管的传热恶化程度更加严重,此时波纹管仍可大幅度减轻传热恶化,相比于光滑管,波纹管可将外壁面最高温度降低约280 K,通过表3可以看出,此时波纹管依然具有很好的综合换热性能。
图18给出了加热段沿程压力随壁面热流的变化情况。由图可以看出压降随热流增大而增大。为了说明强化换热随壁面热流的变化规律,继续研究了1 MW/m2的低热流密度下的换热效果,分析换热性能,如表3所示。当热流密度在1~3 MW/m2之间时,热流密度越大则性能系数越大;当热流密度大于3 MW/m2时随着热流增大综合换热性能有所降低,但换热增加程度仍大于阻力增加程度。
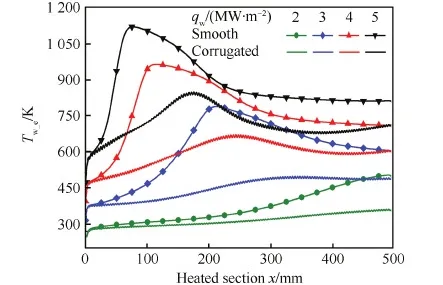
图16 不同壁面热流密度冷却通道外壁面温度变化 Fig.16 Variations of exterior surface temperature of cooling tubes with different wall heat fluxes
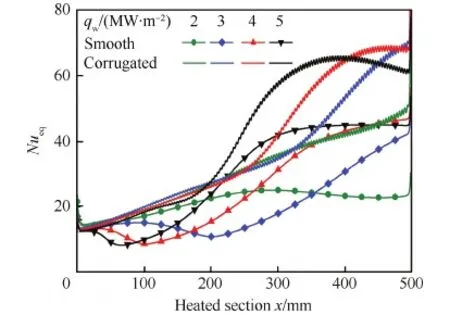
图17 不同壁面热流密度冷却通道等效努塞尔数变化 Fig.17 Variations of equivalent Nusselt number of cooling tubes with different wall heat fluxes
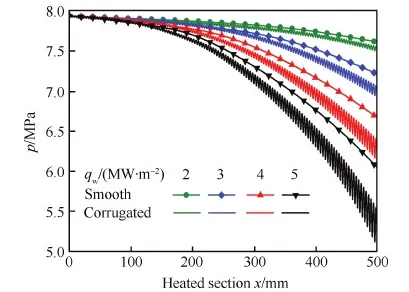
图18 不同壁面热流密度冷却通道沿程压力变化 Fig.18 Variations of pressure along cooling tubes with different wall heat fluxes
表3 不同壁面热流密度冷却通道综合换热性能系数
Table3Overallthermalperformancefactorscalculatedforcoolingtubeswithdifferentwallheatfluxes
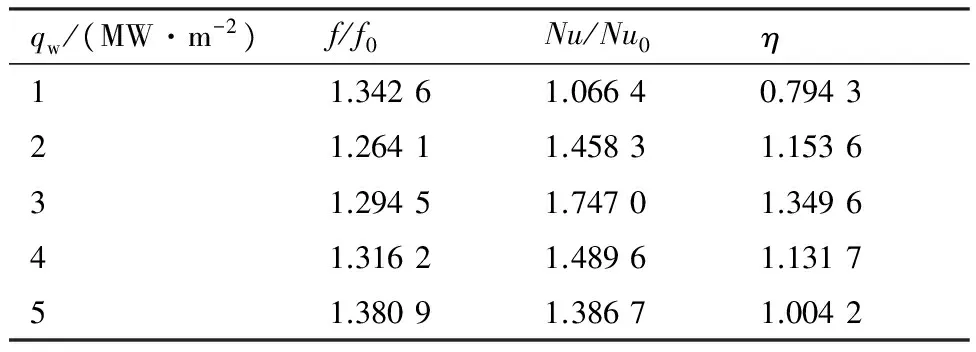
qw/(MW·m-2)f/f0Nu/Nu0η11.34261.06640.794321.26411.45831.153631.29451.74701.349641.31621.48961.131751.38091.38671.0042
2.4 入口压力的影响
由于燃烧室压力不断提升,需要提高冷却通道入口压力实现燃料喷射,所以需要研究压力对强化换热的影响。本节选择选择6~12 MPa之间的入口压力对波高H=0.07 mm的波纹管进行研究,其他工况与2.1节相同。
图19和图20分别为不同压力下冷却通道加热段外壁面温度和等效努塞尔数沿流向变化情况。光滑管道在6 MPa时出现了严重的传热恶化,但是随着压力升高换热效果明显改善,所以通常提高压力可以增强换热效果[25-27]。使用波纹管时,各入口压力下均可完全消除传热恶化,即使在6 MPa时,其换热效果也远好于光滑管在12 MPa 时的换热效果。通过分析波纹管外壁面温度和等效努塞尔数,发现随着压力升高冷却效果显著提升。
图21为不同压力下冷却通道加热段沿程压力变化,发现增大压力后波纹管和光滑管压降都有所降低。表4为不同入口压力下波纹管的综合换热性能系数,可以看出波纹管在该压力范围内均具有良好的综合换热性能。
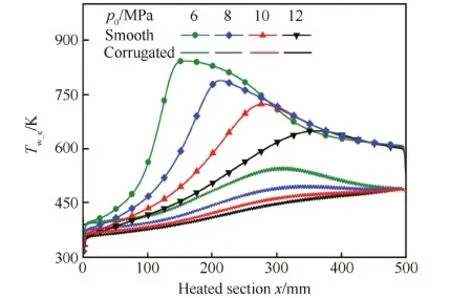
图19 不同入口压力下冷却通道外壁面温度变化 Fig.19 Variations of exterior surface temperature of cooling tubes with different inlet pressures
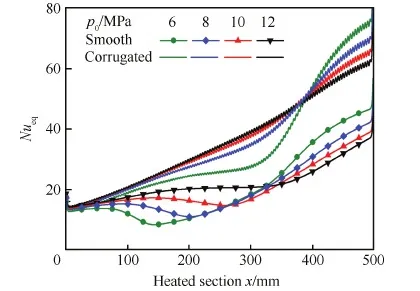
图20 不同入口压力下冷却通道等效努塞尔数变化 Fig.20 Variations of equivalent Nusselt number of cooling tubes with different inlet pressures
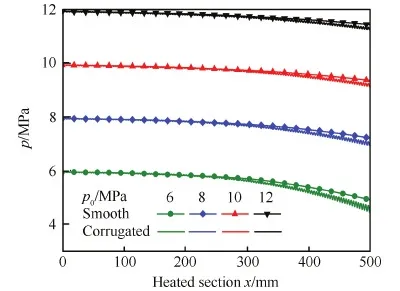
图21 不同入口压力下冷却通道沿程压力变化 Fig.21 Variations of pressure along cooling tubes with different inlet pressures
表4不同入口压力下冷却通道综合换热性能系数
Table4Overallthermalperformancefactorscalculatedforcoolingtubeswithdifferentinletpressures
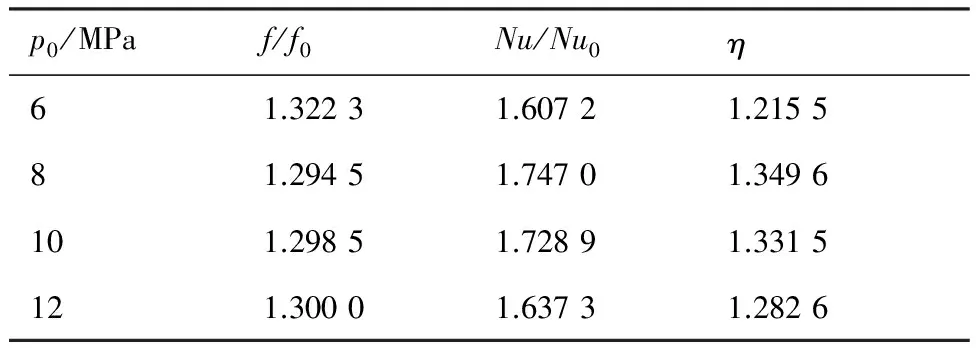
p0/MPaf/f0Nu/Nu0η61.32231.60721.215581.29451.74701.3496101.29851.72891.3315121.30001.63731.2826
2.5 雷诺数的影响
当发动机工作状态不同时,冷却剂入口雷诺数也会发生变化。本节主要讨论入口雷诺数对波纹管强化换热和阻力特性的影响。选择波高H=0.07 mm的波纹管进行研究,入口速度在10~25 m/s 之间选择,则对应的入口雷诺数变化范围为7.72×104~1.93×105。其他工况与2.1节相同。
图22和图23分别为不同雷诺数冷却通道加热段外壁面温度和等效努塞尔数变化情况。从图中可以看出在较低雷诺数Re=7.72×104时,光滑管x=100 mm附近出现了严重的传热恶化,此时波纹管加热段两端强化换热明显,而在中间位置(200 mm≤x≤300 mm)强化换热程度较弱,外壁面最高温度比光滑管降低了约230 K。随着雷诺数增加,当Re=1.16×105时,波纹管的强化换热效果更加显著,此时加热段大部分位置等效努塞尔数均明显增大,波纹管外壁面最高温度比光滑管降低约300 K。继续增大雷诺数,当Re=1.54×105时,加热段下游(x≥200 mm)强化换热明显,而在上游强化换热程度较弱,此时波纹管外壁面最高温度比光滑管降低约260 K。当Re=1.93×105时,仅在加热段下游出口附近(x≥400 mm)强化换热明显,外壁面最高温度比光滑管降低约170 K,整体强化换热程度有所下降。
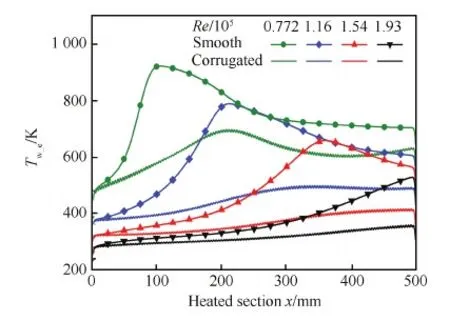
图22 不同雷诺数冷却通道外壁面温度变化 Fig.22 Variations of exterior surface temperature of cooling tubes with different Reynolds numbers
图24为不同雷诺数冷却通道加热段沿程压力变化。雷诺数变化对加热段进出口压降影响不大,但增大雷诺数后加热段各处压力都有所降低。因为管道入口压力均为8 MPa,这就说明在加热段上游长度为150 mm的光滑壁面绝热段中,压降随雷诺数增加迅速增大。
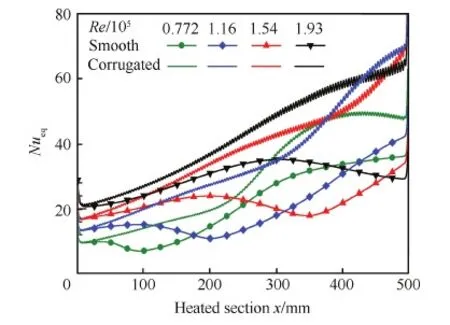
图23 不同雷诺数冷却通道等效努塞尔数变化 Fig.23 Variations of equivalent Nusselt number of cooling tubes with different Reynolds numbers
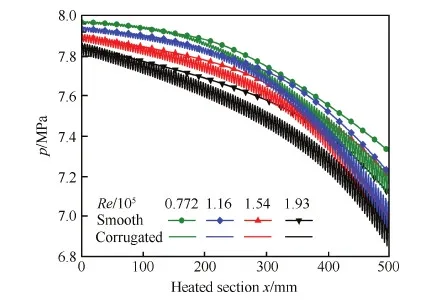
图24 不同雷诺数冷却通道沿程压力变化 Fig.24 Variations of pressure along cooling tubes with different Reynolds numbers
表5给出了不同雷诺数冷却通道的换热增加程度、阻力增加程度以及综合换热性能系数η。通过分析综合换热性能系数随雷诺数的变化情况,发现在该雷诺数范围内始终满足η>1,并且存在一个最佳雷诺数,该雷诺数下波纹管具有最优的综合换热性能。
表5不同雷诺数冷却通道综合换热性能系数
Table5OverallthermalperformancefactorscalculatedforcoolingtubeswithdifferentReynoldsnumbers
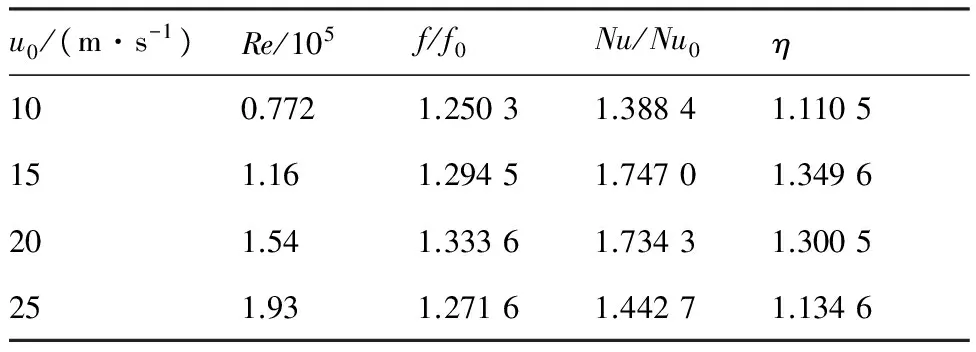
u0/(m·s-1)Re/105f/f0Nu/Nu0η100.7721.25031.38841.1105151.161.29451.74701.3496201.541.33361.73431.3005251.931.27161.44271.1346
3 结 论
1) 在超临界压力下合理选择波纹管可以显著提升强化换热能力,减轻或消除传热恶化,同时不会带来明显的阻力;波纹管换热能力与波高密切相关,存在一个最优波高使得综合换热性能系数达到最大,此时波纹管具有最优的综合换热性能。
2) 增加壁面导热系数有助于提高波纹管综合换热性能,并且不会带来额外的压降损失。
3) 在不同热流密度下波纹管强化换热能力有所不同,热流密度低于3 MW/m2时,随着热流密度增大综合换热性能系数明显增大;当热流密度大于3 MW/m2时,综合换热性能系数随热流增大而减小,但在高热流密度(5 MW/m2)时波纹管依然具有很好的综合换热性能。
4) 入口压力在6~12 MPa变化时,波纹管均具有良好的综合换热性能,且增大压力有利于增强换热能力。
5) 雷诺数在7.72×104~1.93×105范围内变化时,波纹管综合换热性能系数η均大于1,并且存在一个最佳雷诺数使综合换热性能最优。
[1] SUTTON G P, BIBLARZ O. Rocket propulsion elements[M]. 7th ed. New York: John Wiley & Sons, 2001.
[2] PRECLIK D, WIEDMANN D, OECHSLEIN W, et al. Cryogenic rocket calorimeter chamber experiments and heat transfer simulations[C]//The 34th AIAA/ASME/SAE/ ASEE Joint Propulsion Conference and Exhibit. Reston: AIAA, 1998.
[3] XU K K, TANG L J, MENG H. Numerical study of supercritical-pressure fluid flows and heat transfer of methane in ribbed cooling tubes[J]. International Journal of Heat and Mass Transfer, 2015, 84: 346-358.
[4] 谢凯利. 小尺度矩形通道内碳氢燃料流动及强化传热研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
XIE K L. Study on flow and enhanced heat transfer of hydrocarbon fuel in small-scale rectangular channels[D]. Harbin: Harbin Institute of Technology, 2015 (in Chinese).
[5] 陈建华, 张贵田, 吴海波, 等. 高压推力室人为粗糙度煤油强化换热实验[J]. 实验流体力学, 2008, 22(4): 34-38.
CHEN J H, ZHANG G T, WU H B, et al. Investigation of heat transfer enhancement with artificial roughness for high pressure chamber using kerosene as coolant[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(4): 34-38 (in Chinese).
[6] KAREEM Z S, JAAFAR M N M, LAZIM T M, et al. Passive heat transfer enhancement review in corrugation[J]. Experimental Thermal and Fluid Science, 2015, 68: 22-38.
[7] 肖金花, 钱才富, 黄志新. 波纹管传热强化效果与机理研究[J]. 化学工程, 2007, 35(1): 12-15.
XIAO J H, QIAN C F, HUANG Z X. Study of effects and mechanisms of heat transfer enhancement of corrugated tubes[J]. Chemical Engineering, 2007, 35(1): 12-15 (in Chinese).
[8] 曾敏, 王秋旺, 屈治国, 等. 波纹管内强制对流换热与阻力特性的实验研究[J]. 西安交通大学学报, 2002, 36(3): 237-240.
ZENG M, WANG Q W, QU Z G, et al. Experimental study on the pressure drop and heat transfer characteristics in corrugated tubes[J]. Journal of Xi’an Jiaotong University, 2002, 36(3): 237-240 (in Chinese).
[9] YANG D, LI H X, CHEN T K. Pressure drop, heat transfer and performance of single-phase turbulent flow in spirally corrugated tubes[J]. Experimental Thermal and Fluid Science, 2001, 24(3-4): 131-138.
[10] VICENTE P G, GARCA A, VIEDMA A. Mixed convection heat transfer and isothermal pressure drop in corrugated tubes for laminar and transition flow[J]. International Communications in Heat and Mass Transfer, 2004, 31(5): 651-662.
[11] VICENTE P G, GARCIA A, VIEDMA A. Experimental investigation on heat transfer and frictional characteristics of spirally corrugated tubes in turbulent flow at different Prandtl numbers[J]. International Journal of Heat and Mass Transfer, 2004, 47(4): 671-681.
[12] BARBA A, RAINIERI S, SPIGA M. Heat transfer enhancement in a corrugated tube[J]. International Communications in Heat and Mass Transfer, 2002, 29(3): 313-322.
[13] LAOHALERTDECHA S, WONGWISES S. The effects of corrugation pitch on the condensation heat transfer coefficient and pressure drop of R-134a inside horizontal corrugated tube[J]. International Journal of Heat and Mass Transfer, 2010, 53(13-14): 2924-2931.
[14] POLING B E, PRAUSNITZ J M, JOHN P O, et al. The properties of gases and liquids[M]. New York: McGraw-Hill, 2001.
[15] LEMMON E W, SPAN R. Short fundamental equations of state for 20 industrial fluids[J]. Journal of Chemical & Engineering Data: the ACS Journal for Data, 2006, 51(3): 785-850.
[16] SETZMANN U, WAGNER W. A new equation of state and tables of thermodynamic properties for methane covering the range from the melting line to 625 K at pressures up to 100 MPa[J]. Journal of Physical and Chemical Reference Data, 1991, 20(6): 1061-1155.
[17] FRIEND D G, ELY J F, INGHAM H. Thermophysical properties of methane[J]. Journal of Physical and Chemical Reference Data, 1989, 18(2): 583-638.
[18] HUBER M L, LAESECKE A, XIANG H W. Viscosity correlations for minor constituent fluids in natural gas:n-octane,n-nonane andn-decane[J]. Fluid Phase Equilibria, 2005, 228-229: 401-408.
[19] HUBER M L, PERKINS R A. Thermal conductivity correlations for minor constituent fluids in natural gas:n-octane,n-nonane andn-decane[J]. Fluid Phase Equilibria, 2005, 227(1): 47-55.
[20] National Institute of Standards and Technology. Thermophysical properties of fluid systems[DB/OL]. (2015-02-09)[2016-04-25]. http://webbook.nist.gov/chemistry/fluid.
[21] LIU B, ZHU Y H, YAN J J, et al. Experimental investigation of convection heat transfer ofn-decane at supercritical pressures in small vertical tubes[J]. International Journal of Heat and Mass Transfer, 2015, 91: 734-746.
[22] URBANO A, NASUTI F. Parametric analysis of heat transfer to supercritical-pressure methane[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(3): 450-463.
[23] WANG L L, CHEN Z J, MENG H. Numerical study of conjugate heat transfer of cryogenic methane in rectangular engine cooling channels at supercritical pressures[J]. Applied Thermal Engineering, 2013, 54(1): 237-246.
[24] 何雅玲, 陶文铨, 王煜, 等. 换热设备综合评价指标的研究进展[C]//中国工程热物理学会学术会议论文. 北京: 中国工程热物理学会, 2011.
HE Y L, TAO W Q, WANG Y, et al. Research progress on performance evaluation criteria of heat transfer equipment[C]//National Conference of Chinese Society of Engineering Thermophysics. Beijing: Chinese Society of Engineering Thermophysics, 2011 (in Chinese).
[25] RUAN B, MENG H. Supercritical heat transfer of cryogenic-propellant methane in rectangular engine cooling channels[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(2): 313-321.
[26] 王亚洲, 华益新, 孟华. 超临界压力下低温甲烷的湍流传热数值研究[J]. 推进技术, 2010, 31(5): 606-611.
WANG Y Z, HUA Y X, MENG H. Numerical investigation of turbulent heat transfer of cryogenic-propellant methane under supercritical pressures[J]. Journal of Propulsion Technology, 2010,31(5): 606-611 (in Chinese).
[27] WANG Y Z, HUA Y X, MENG H. Numerical studies of supercritical turbulent convective heat transfer of cryogenic-propellant methane[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(3): 490-500.
(责任编辑: 彭健, 李明敏)
URL:www.cnki.net/kcms/detail/11.1929.V.20160823.1615.004.html
Numericalinvestigationofheattransferenhancementofcryogenic-propellantmethaneincorrugatedtubesatsupercriticalpressures
HUANGShizhang,RUANBo,GAOXiaowei*
SchoolofAeronauticsandAstronautics,DalianUniversityofTechnology,Dalian116024,China
Theactiveregenerativecoolingsystemoftherocketengineisstudied,andamethodisdevelopedtogiveanaccurateestimationofthermophysicalproperties.Anumericalinvestigationofconvectiveheattransferofcryogenic-propellantmethaneinhorizontalcorrugatedtubesatsupercriticalpressuresisconducted.Theheattransferenhancementmechanismofcorrugatedtubesisanalyzed.Theeffectsofseveralkeyinfluentialparametersonbothheattransferenhancementandpressuredropareinvestigated,includingthepitch-to-heightratio,wallthermalconductivity,wallheatflux,inletpressure,andReynoldsnumber.Theperformanceevaluationcriteriaareadoptedtoevaluatethethermalperformanceinfluencedbytheseparameters.Resultsrevealthatreasonablecorrugatedtubescansignificantlyimprovetheheattransferabilitywithoutcausingsignificantpressuredropatsupercriticalpressures,whichisbeneficialtotheeliminationofheattransferdeterioration.ThereexistanoptimumcorrugationheightandReynoldsnumberforachievingthebestoverallthermalperformance.Increaseofwallthermalconductivityandinletpressurecanimprovetheheattransferability.
supercriticalpressure;cryogenic-propellantmethane;corrugatedtube;heattransferenhancement;activeregenerativecooling
2016-06-11;Revised2016-07-07;Accepted2016-07-31;Publishedonline2016-08-231615
s:NationalNaturalScienceFoundationofChina(11172055);ChinaPostdoctoralScienceFoundation(2014M561235)
.E-mailxwgao@dlut.edu.cn
2016-06-11;退修日期2016-07-07;录用日期2016-07-31; < class="emphasis_bold">网络出版时间
时间:2016-08-231615
www.cnki.net/kcms/detail/11.1929.V.20160823.1615.004.html
国家自然科学基金 (11172055); 中国博士后科学基金 (2014M561235)
.E-mailxwgao@dlut.edu.cn
黄世璋, 阮波, 高效伟. 超临界压力低温甲烷波纹管内强化换热数值研究J. 航空学报,2017,38(5):120515.HUANGSZ,RUANB,GAOXW.Numericalinvestigationofheattransferenhancementofcryogenic-propellantmethaneincorrugatedtubesatsupercriticalpressuresJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120515.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0227
V434+.14
A
1000-6893(2017)05-120515-14
