波转子非定常泄漏流动机理
2017-11-20刘琛源刘火星
刘琛源, 刘火星
北京航空航天大学 能源与动力工程学院, 北京 100083
波转子非定常泄漏流动机理
刘琛源, 刘火星*
北京航空航天大学 能源与动力工程学院, 北京 100083
针对制约波转子性能的泄漏问题,通过提取波转子中与泄漏相关的主要流动现象并建立波转子单通道泄漏模型,对非定常泄漏流动机制进行了详细的数值研究,对本文给出的非定常泄漏损失预测模型进行了数值验证。结果表明:转子通道中存在不同程度的压力波动,波动幅值与间隙宽度有关;连续反射膨胀波、周期性出现的弓形激波及其反射激波是压力波动的根本原因;间隙内部泄漏过程存在3个主要的流动阶段;泄漏过程中通道激波传播速度不变、波后时均压力不变;在一定间隙宽度范围内,激波马赫数、激波静增压比与无量纲间隙宽度均呈线性关系,当间隙宽度从0增大到0.08时,激波马赫数衰减7.3%,激波静增压比衰减10.1%;泄漏流动通过泄漏产生的主膨胀波对激波传播过程施加影响,通道激波衰减本质上是理想激波与主膨胀波叠加效应的结果;泄漏损失预测模型与数值结果吻合良好。
燃气轮机; 波转子; 单通道模型; 非定常泄漏流动; 激波
20世纪初人们便已认识到非定常流动巨大的应用前景,但是非定常流动自身的复杂性在很长一段时期内阻碍了波转子技术的发展和应用[1]。近年来,随着气动设计的不断完善以及材料性能的限制,传统燃气轮机逐渐达到性能极限[2]。波转子通过运动激波和膨胀波直接在不同状态的气体间交换能量,因此具备巨大的增压潜力以及相对较高的增压效率[3];另外,由于能量交换过程不需要压气机和涡轮叶片,结构相对简单,因此能够有效降低发动机结构重量及制造成本[4]。
基于波转子的工作特点,相比传统燃气轮机它还具有以下几个优势:① 转子转速相对较低,因此材料应力小;② 响应迅速,响应时间与压力波的特征时间尺度为相同量级;③ 转子通道内工质流速低,仅为典型的叶轮机械工质流速的1/3左右[5],因此通道壁面更耐腐蚀;④ 空气和燃气交替通过转子通道,具有自冷却效应,可以承受更高的燃气温度。
波转子技术具有大幅提高现有发动机性能的潜力,但是仍然存在一些技术障碍亟需克服,主要体现在3个方面:1)气动设计,即如何根据给定的应用需求确定最佳设计参数、同时解决非设计点性能问题[4];2)结构设计,主要解决转静部件间的热膨胀及密封问题[4];3)损失机理分析及损失评估[6],波转子内部损失主要包括:① 非定常波系损失,包括激波固有的熵增损失以及膨胀波后流动不均匀带来的掺混损失;② 转子通道非瞬时开闭损失,通道非瞬时开闭使触发的波系偏离理想波系,进一步形成包含激波、旋涡在内的复杂流动结构,流动的紊乱会对波转子性能产生不利影响;③ 非轴向进气损失,与通道非瞬时开闭具有类似的损失机制;④ 摩擦损失,转子通道一般具有较大的相对表面积,壁面摩擦不可忽略;⑤ 泄漏损失,波系在端壁反射引起通道、端口、转子容腔之间的压力差,进而引起泄漏。
波转子气动设计方法研究较为完善,但是针对流动损失机理的研究相对较少,这在一定程度上限制了波转子技术的发展和应用。Wilson[6]针对商用波转子Comprex研究了各类损失对效率的影响,Wilson指出,泄漏损失在所有损失中占主导地位,特别对于小型波转子,泄漏对性能的影响更为突出。Wilson[6]在三端口和四端口波转子实验中发现泄漏对波转子性能下降影响很大。
目前在世界范围内,针对泄漏流动主要通过泄漏模型计入其对性能的影响,包括广泛应用于波转子准一维设计程序的单容腔模型[7]以及Akbari和Nalim[8]提出的分段泄漏模型。上述2种模型均未考虑具体流动过程,特别是泄漏流动和主流的相互作用。由于运动激波在波转子的工作机制中起着重要作用,因此了解泄漏对激波传播特性以及波后流场的影响非常重要。本文采用数值研究手段详细分析了波转子的泄漏流动及损失机制,并提出了泄漏损失预测模型。
1 波转子工作过程及泄漏流动特征
图1给出了一种典型的用于航空燃气轮机循环的四端口通流外燃波转子结构[2]及实验装置[9],它由旋转鼓筒及鼓筒两侧的静止端板构成,转子通道位于旋转鼓筒上。鼓筒高速旋转,转子通道与各个端口周期性地连通、闭合,从而在通道内部触发运动的激波和膨胀波。压气机出口空气通过低压空气(LPA)端口进入转子通道,燃烧室出口燃气则通过高压燃气(HPG)端口进入转子通道,燃气与空气接触后触发运动激波,空气经激波增压后通过高压空气(HPA)端口进入燃烧室,最后燃气膨胀后经低压燃气(LPG)端口进入涡轮,从而完成整个热力循环过程。
通过波系的压缩和膨胀作用,流入流出4个端口的气体快速完成能量交换,最终使得来自压气机的空气在更高的压力和温度下进入燃烧室燃烧,从而提高整个燃气轮机的热力循环效率,同时保证膨胀后进入涡轮的燃气压力高于压气机出口的空气压力,从而提高涡轮输出功率。
波转子发生泄漏的根本原因是转子通道依次通过各个端口时,在每个通道末端触发的激波或膨胀波之间存在一定时滞,因此在通道末端同一时刻不同通道内的气体压力可能不同,高压通道气体通过转静间隙进入低压通道引起周向泄漏,通道与容腔之间的压力差则引起径向泄漏。
图2给出了波转子高压循环的波系结构。如图2所示,当入射激波(Incident shock wave)到达通道右端时,立即产生一道向左端传播的反射激波(Reflected shock wave),反射激波波后气体此时位于高压区域2中,经过两道激波的增压作用,2区气体压力明显高于1区以及转子容腔压力,2区通道内的高压气体经转静间隙分别泄漏到容腔以及1区通道内部。
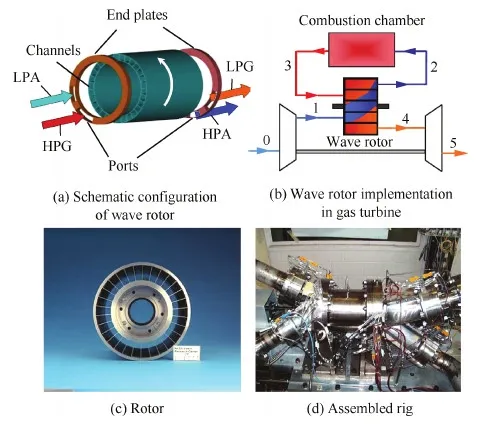
图1 典型的四端口通流波转子结构及实验装置[2,9]Fig.1 Typical structure of four-port through-flow wave rotor and experimental apparatus[2,9]
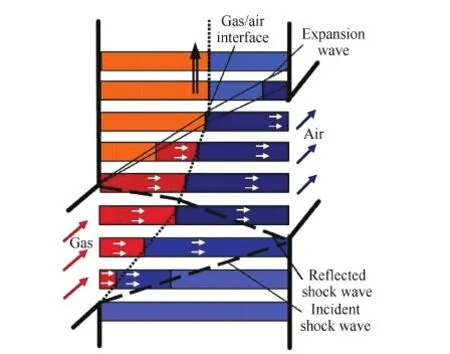
图2 波转子高压循环波系结构 Fig.2 Wave diagram of high-pressure part of wave rotor
2 泄漏分析数值模型
数值模型通过构造黎曼间断形成通道内的运动激波[10]。由于波转子内部存在通道非瞬时开闭、非轴向进气等多种损失,为了深入分析泄漏损失机理,通过建立二维单通道泄漏模型,隔离其他损失因素对泄漏流动的影响,图3给出了该模型的几何示意图。
激波强度、波前气体状态、气体物性以及通道截面尺寸等均对激波传播特性存在影响。Glass 和Patterson[11]通过实验研究发现,激波静压比小于3时,在一定距离内,激波传播速度不变;静压比大于3时,最大波速低于理论值,并且在传播过程中波速逐渐减小。另外,随着通道截面尺寸减小,气体黏性效应、稀薄效应和壁面传热效应越来越显著,从而导致激波在传播过程中不断衰减[12]。
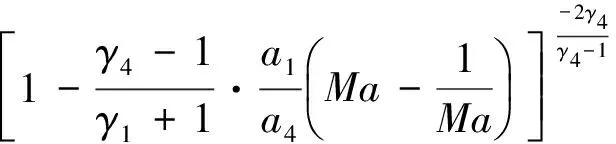
(1)
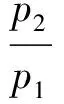
(2)
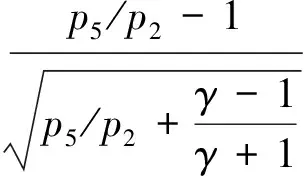
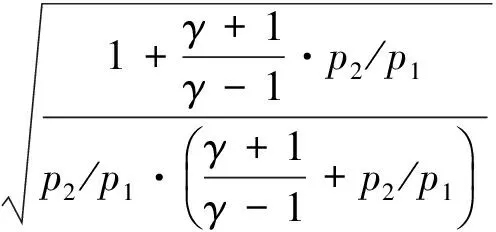
(3)
式中:pi为压力;ai为声速;γi为比热比;Ma为入射激波马赫数;i=1,2,4,5。
为了准确反映激波在波转子通道中的传播特性,需要选择合适的气动参数和模型尺寸。四端口通流波转子增压比通常在2.5~3.5之间,此时通道进口触发的激波静压比小于2。本文给定泄漏模型低压段初始压力为101 325 Pa、高压段初始压力为405 300 Pa,初始温度均为298.15 K,初始时刻气体均静止,工质为采用理想气体模型的空气。设初始时刻低压段为1区、高压段为4区,入射激波形成后波后为2区,反射激波波后为5区,根据式(1)~式(3),泄漏流量为零时的理论参数如下:入射激波压比p2/p1=1.93;反射激波压比p5/p2=1.82;总增压比p5/p1=3.51。数值模型几何参数选择参考表1[13],具体尺寸在图3中给出。

图3 波转子二维单通道泄漏模型 Fig.3 Two-dimensional model for single passage leakage of wave rotor
表1 典型波转子构型的主要几何参数[13]Table 1 Main geometric parameters of typical configurations of wave rotor[13]
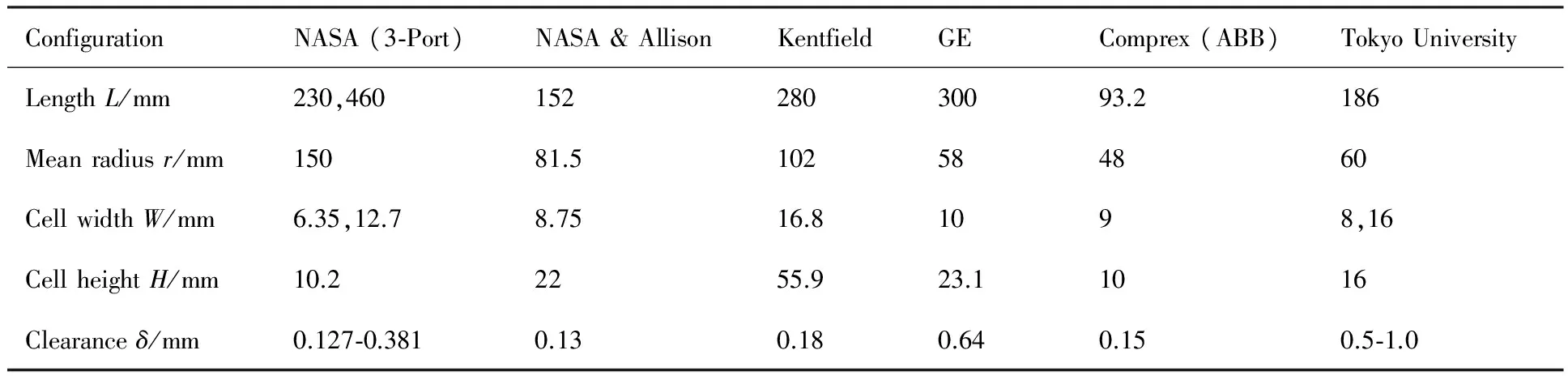
ConfigurationNASA(3⁃Port)NASA&AllisonKentfieldGEComprex(ABB)TokyoUniversityLengthL/mm230,46015228030093.2186Meanradiusr/mm15081.5102584860CellwidthW/mm6.35,12.78.7516.81098,16CellheightH/mm10.22255.923.11016Clearanceδ/mm0.127⁃0.3810.130.180.640.150.5⁃1.0
3 数值模型求解方法及验证
3.1 数值模型
数值模型各算例泄漏间隙宽度最小值为0.1 mm,间隙内部流动Kn数约为5.6×10-4,因此所有算例均可采用基于连续介质假设的Navier-Stokes方程进行数值求解[14]。
选择FLUENT 12.1密度基隐式求解器,流动控制方程对流项离散采用AUSM+(Advection Upstream Splitting Method)格式[15],对流通量计算进行三阶MUSCL(Monotonic Upwind Scheme for Conservation Laws)插值,黏性项离散采用中心差分格式,时间项离散采用二阶隐式格式,湍流模拟选择Spalart-Allmaras一方程模型。如图3所示,Symmetry采用对称面边界条件[16],其他模型边界均选择无滑移绝热壁面。所有算例物理时间步最大值为10-8s,当激波传播到通道末端时调整为5×10-10s;虚拟时间步设置保证方程残差不再减小;数值模拟总时间为0.42 ms。计算域离散采用四边形结构化网格,距壁面第一层网格高度y+最大值为0.001 mm,从而保证所有算例y+值小于1;平行壁面方向网格最大间距为0.1 mm;在间隙内部对网格进行局部加密,垂直壁面方向最大网格间距为0.01 mm;网格总数为22万,经网格无关性验证,证明上述网格可以很好地捕捉激波。工质采用理想气体模型,空气动力黏性系数根据萨瑟兰定律确定,定压比热计算采用分段多项式法。
3.2 数值方法验证
针对本文采用的数值方法,需要重点考察以下2点:① 存在黏性效应的情况下求解器对一维运动激波的捕捉能力;② 数值格式对非定常流场中复杂二维波系及其相互作用的模拟能力。
为了考察数值格式对一维运动激波的模拟精度,选择日本东北大学无膜激波管实验对数值方法进行校验。图4给出了实验装置[17]和相应的数值模型,其中被驱动段初始压力为10 000 Pa,入射激波马赫数为1.2,计算域初始温度为297 K,入射激波进入微尺度通道后,5个等间距布置的压力测点(P1~P5)依次记录激波通过后流场的压力变化,图5给出了实验及数值结果,p为压力,采用被驱动段初始压力进行无量纲化,t为时间。对于激波强度、波速以及激波的沿程衰减,数值和实验结果吻合良好。
为了验证数值格式对二维非定常流动的模拟能力,考察入射激波在泄漏间隙内的绕射过程。激波绕射是一种典型的自相似现象[18],因此可以将激波在间隙内的绕射流场及无量纲流动参数与激波绕射实验结果进行对比,校验本文数值方法。数值校验共考察了入射激波马赫数Ma=1.5和Ma=2.0两个算例。
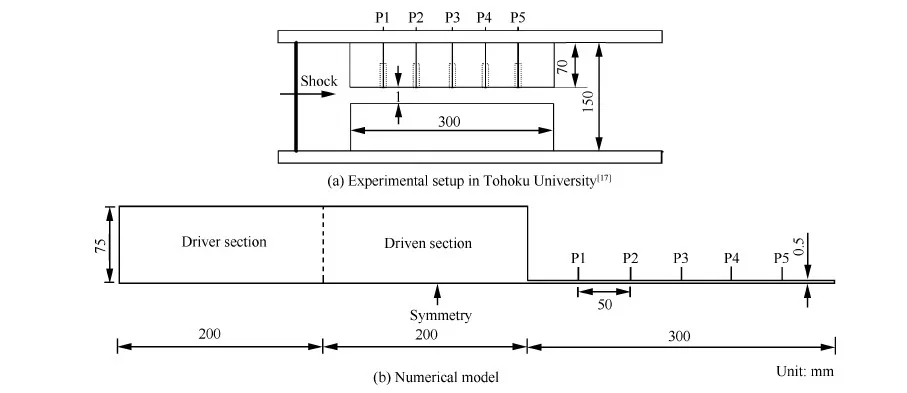
图4 无膜激波管实验装置简图及数值模型 Fig.4 Experimental setup of diaphragmless shock tube and numerical model
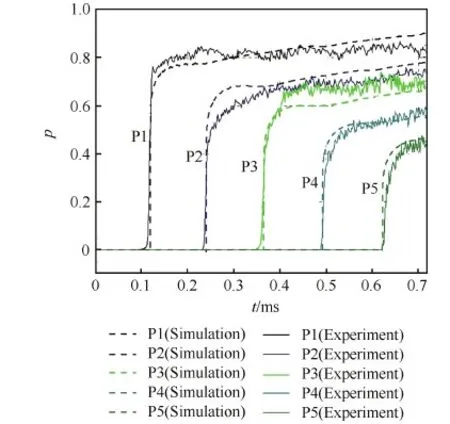
图5 激波管各测点压力随时间变化 Fig.5 Variation of pressure with time at different test locations in shock tube
(1) 流动结构验证
对于Ma=1.5算例,图6(a)给出的泄漏间隙激波绕射密度等值线图和图6(b)[19]给出的实验结果均清晰地显示出转角处局部膨胀波和剪切层上缘激波构成的的λ波结构;对比图6(c)和图6(d)[19]可以看到,数值模拟较好地表现了绕射激波波后接触面环绕旋涡并与剪切层前缘下表面融合的现象。
随着入射激波马赫数提高到2.0,绕射激波波后流动结构发生局部变化,转角处λ波的膨胀波分支演变为与普朗特迈耶流类似的中心膨胀波,λ波的激波分支沿剪切层上表面向后移动到剪切层尾部,同时强度大大增强,形成一道S形激波;图7(a)的数值结果和图7(d)[20]的实验结果均可观察到典型的S形激波。
Skews[18]指出,对于Ma=2.0的入射激波,剪切层形状基本保持为直线,仅在其尾部向旋涡一侧弯曲,对于绕射激波波后间断面,与低马赫数入射激波情况相同的是间断面均在靠近旋涡时环绕旋涡,但在接近剪切层时,间断面突然转向并以直线形式连接转角顶点。对比图6(c)和图7(c)给出的流场熵增分布,可以观察到入射激波马赫数变化时剪切层和间断面形状的改变;另外,Ma=2.0时,从90° 转角顶点处沿径向形成一道新的间断面,即中心膨胀波波尾,该间断面与S形激波上缘相交。

图6 Ma=1.5入射激波直角绕射数值和实验结果对比 Fig.6 Comparison between numerical and experimental results for incident shock of Mach number 1.5 diffracting at corner of ninety degrees

图7 Ma=2.0入射激波直角绕射数值和实验结果对比 Fig.7 Comparison between numerical and experimental results for incident shock of Mach number 2.0 diffracting at corner of ninety degrees
(2) 流场参数验证
图8为激波初始折转角和剪切层角度示意图。图中:EW为膨胀波波头;IS为入射激波;SL为剪切层;V为旋涡;W为壁面。考察入射激波初始折转角m0、剪切层角度e0、壁面激波马赫数Maw、旋涡移动速度u随入射激波马赫数变化,评估数值方法对激波膨胀波相互作用、气流分离与剪切、旋涡运动等非定常流动现象的模拟精度。图9给出了Ma=1.5、Ma=2.0算例数值结果和相应的实验结果,除Ma=2.0算例剪切层角度预测偏差略大外,其他参数均吻合较好。
通过详细的数值校验,发现本文采用的数值方法可以准确模拟激波传播、低雷诺数下的激波衰减以及激波、膨胀波相互作用、旋涡运动、滑移间断等非定常流动现象。
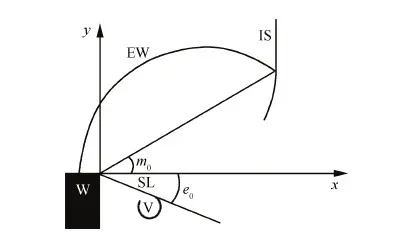
图8 激波初始折转角和剪切层角度示意图 Fig.8 Schematic diagram of shock diffraction angle and shear layer angle
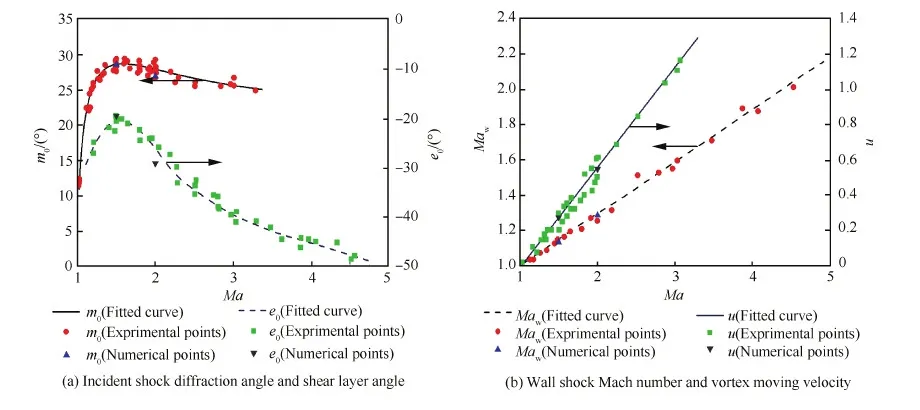
图9 典型流场参数随入射激波马赫数变化数值和实验结果对比 Fig.9 Comparison between numerical and experimental results for change of typical flow parameters with incident shock Mach number
4 计算结果分析
4.1 非定常泄漏流动特征
为了深入分析非定常泄漏流动的发生机制及其对通道内激波传播过程的影响,先考虑不含通道激波的泄漏过程。
(1) 不含通道激波的情况
选择泄漏间隙0.8 mm算例进行分析。图10 给出了泄漏模型初始流场,主通道内气体状态与零间隙宽度下反射激波波后状态相同。在大于零时刻瞬间,一道激波在间隙入口形成并通过泄漏间隙进入副通道,膨胀波形成后在主通道(以下简称通道)中传播。
图11给出了不同时刻通道内压力分布,压力数据采用通道初始压力进行无量纲化。观察图11 发现,在壁面和通道中心截面(Symmetry)之间存在连续反射的二维膨胀波和周期性出现的二维激波及其反射激波。

图10 不含通道激波时泄漏模型初始流场 Fig.10 Initial flow field of leakage model without channel shock wave
观察图11(a),泄漏流动开始瞬间,在间隙入口处形成了一道扇形膨胀波,由于在膨胀波传播方向流道几何非对称,膨胀波宽度沿波面出现不均匀性,引起波后气流折转,因此膨胀波后又形成一道弓形激波;膨胀波到达通道中心截面时,与另一侧间隙处形成的膨胀波相交并相互穿过(可以理解为波在虚拟固壁上的反射),在0.014 ms时可以清晰地观察到对称面附近的反射膨胀波,紧接着,激波到达对称面并发生反射,在0.024 ms时可以清晰地观察到反射激波。
随着第一道反射膨胀波向壁面方向传播,第一道弓形激波传播过程中形成的波后高压区域逐渐被第一道膨胀波及其反射波限制在靠近壁面的三角形区域内,称为下侧高压区,如图11(c)所示。
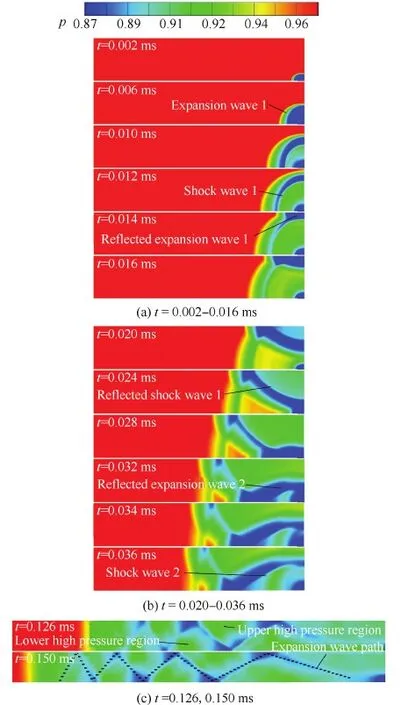
图11 不同时刻通道内压力分布 Fig.11 Pressure distribution in channel at different times
第一道反射膨胀波到达壁面后,再次发生反射,形成第二道反射膨胀波,第一道反射膨胀波的二次反射触发了间隙上游壁面附近第二道弓形激波的形成,图11(b) 0.032 ms、0.036 ms时的压力分布云图分别给出了第二道反射膨胀波和第二道弓形激波的波形。
随着第二道反射膨胀波向对称面方向传播,第一道反射激波形成的波后高压区域逐渐被第一、第二反射膨胀波共同限制在对称面附近,称为上侧高压区,如图11(c)所示。
通过上述作用机制,泄漏发生后的第一道膨胀波(称为主膨胀波)以近一维的形式在通道内传播,泄漏初始时刻主膨胀波在对称面的反射波则在非定常泄漏过程中不断发生反射,并周期性地触发泄漏间隙上游靠近壁面处弓形激波的形成,该弓形激波同样在对称面发生反射;弓形激波及其反射激波形成的高压区域分别被连续反射膨胀波限制在通道壁面及对称面附近。图11(c) 0.15 ms 时的压力云图给出了膨胀波的反射路径。由于膨胀波、激波在通道壁面间的反射作用,通道内气体流动方向不再与壁面平行,而是出现周期性折转,如图12所示。
图13给出了通道中心截面上不同监测点压力随时间的变化曲线,其中P3、P4、P5距通道末端分别为3 cm、2 cm、1 cm。可以看到,主膨胀波通过后各监测点压力均发生大幅下降,随后在激波、局部高压区与连续反射膨胀波的交替作用下压力出现周期性震荡,随着非定常泄漏过程的发展,各监测点压力震荡幅值逐渐减小。
图14进一步给出了各个监测点压力波动频率随波动周期的变化。由于局部高压区范围在传播过程中不断缩小,因此各个监测点压力波动频率随着泄漏过程的进行逐渐降低。
(2) 包含通道激波的情况
对于存在通道激波的泄漏过程,激波在到达通道末端时与间隙泄漏流动存在非定常相互作用,间隙内部流动大致可分为3个阶段:① 通道激波的绕射、反射及传播;② 间隙出口非定常膨胀波的逆向传播及与间隙激波的非定常相互作用;③ 准稳态流动阶段。间隙宽度在一定范围内变化时,前两个阶段流动特征基本不变,仅第3阶段有所区别。

图12 0.126 ms通道内流线分布 Fig.12 Distribution of streamlines in channel at 0.126 ms

图13 通道中心截面不同监测点压力变化曲线 Fig.13 Pressure curves of different monitor points at centerline of channel
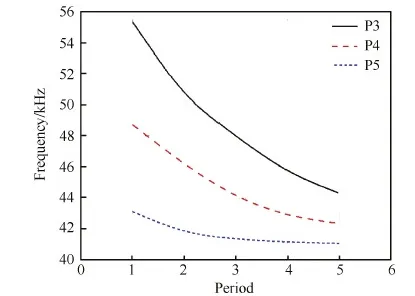
图14 通道中心截面不同监测点压力波动频率随波动周期变化 Fig.14 Variation of pressure oscillation frequency with time of different monitor points at centerline of channel
选择泄漏间隙0.2 mm、0.4 mm、0.8 mm 3个算例进行分析,设通道激波形成瞬时为零时刻,并以间隙宽度为零时通道反射激波波后压力为参考值对流场压力数据进行无量纲化。
图15给出了通道激波在间隙入口绕射、反射的流动发展过程。激波绕射使通道内气体流动方向发生折转,气体开始泄漏到间隙内部;当入射激波到达通道末端发生反射时,入射激波消失,绕射波部分形成一道独立激波在间隙内部传播;反射激波形成后波面向间隙一侧弯曲,待其传播到间隙左侧壁面附近时,与旋涡相互作用同时波面发生分裂,其中上半支越过间隙继续在通道内部传播,下半支则形成一道独立激波在间隙内两侧壁面间来回反射同时向间隙出口传播。
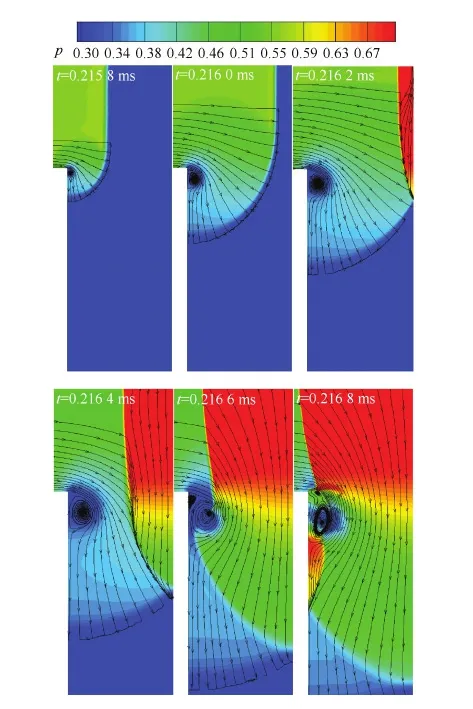
图15 入射激波在通道末端间隙绕射、反射静压云图和流线分布 Fig.15 Static pressure and streamline distribution of incident shock wave diffraction, reflection in leakage gap of channel end
综合以上分析,间隙内共形成了两道激波,正是这两道波触发了初始泄漏流动,其中第一道为入射激波的绕射波分支,第二道为反射激波与旋涡相互作用引起波面分裂后的下半分支;第一道激波强度较弱,第二道激波则较强,并通过在壁面间的反射增加了第一道波的强度。
图16给出了上述两道激波在间隙内的传播过程。可以看到,随着第二道激波在壁面间的不断反射,第一道激波强度不断增强,同时间隙左侧前缘分离泡脱离壁面并向下游移动,新的分离泡又在前缘处重新生成。
当第一道及第二道激波相继到达间隙出口后,分别在出口处反射膨胀波并向上游传播,图17 给出了非定常膨胀波在间隙内的逆向传播过程。
非定常膨胀波使间隙内气体压力不断降低,间隙内部最终会形成如图18所示的准稳态流动结构,图中δ为间隙宽度。当间隙宽度δ变化时,在壁面前缘处形成大小不同的翼型分离泡,分离泡上表面与间隙右侧壁面构成收敛扩张通道。分离泡前缘附近靠近壁面的气流折转最为剧烈,因此该处气流在由亚声加速到超声过程中会在分离泡前缘产生一束较强的定常膨胀波,该膨胀波贯穿泄漏间隙并使进入间隙的气流在收敛扩张通道中加速到超声,在图19中可以观察到大范围的超声流动区。由于在分离泡尾缘流道相对收缩,因此在尾缘处产生一道定常斜激波,该斜激波在间隙右侧壁面反射后引起边界层气流分离,在图18(a)、图18(b)中可以看到右侧壁面超声流动区下游形成的小分离泡。
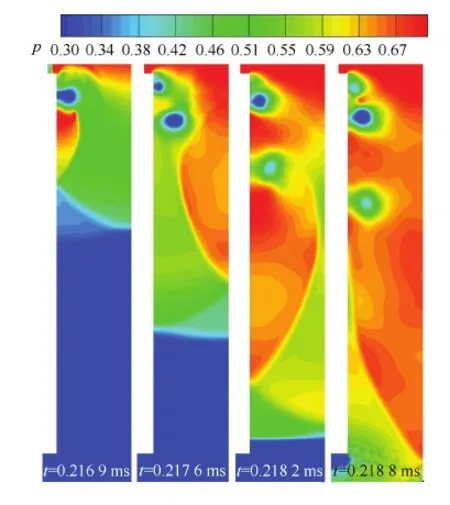
图16 激波在泄漏间隙内的反射及传播过程 Fig.16 Progress of shock wave reflection and propagation in leakage gap
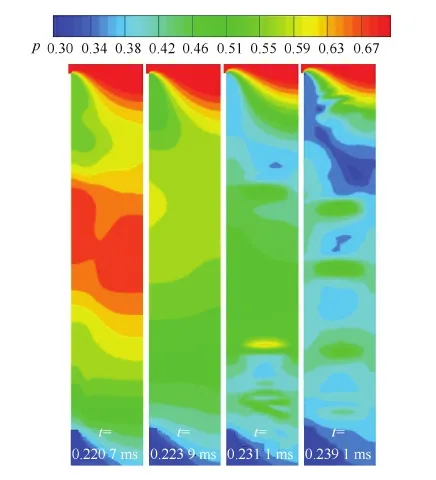
图17 非定常膨胀波在间隙内部的逆向传播过程 Fig.17 Backward propagation of nonsteady expansion waves in leakage gap
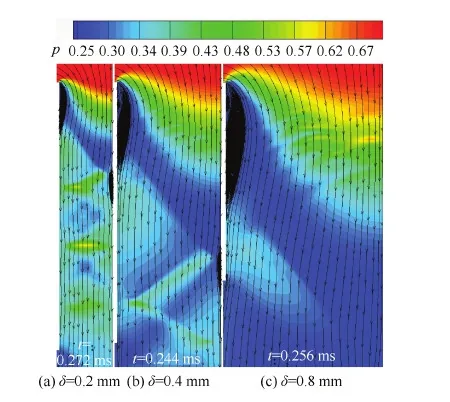
图18 泄漏间隙准稳态流动阶段 Fig.18 Quasi-steady flow period in leakage gap
图20给出了同一时刻间隙宽度δ从0~0.8 mm 变化时通道静压及流线分布。当间隙宽度为零时,反射激波波后压力分布较为均匀,与理论计算结果一致。随着间隙宽度增加,波后出现了连续反射膨胀波、周期性出现的弓形激波及其反射波在通道内传播引起的压力波动以及由此形成的局部高压区和低压区,且波动幅值随着间隙宽度增加而增大。图21给出了压力波动幅值随间隙宽度的变化关系,间隙宽度为0.2 mm时,波动幅值为2%,间隙宽度为0.4 mm时,波动幅值为3.2%,间隙宽度为0.8 mm时,波动幅值为4.4%。
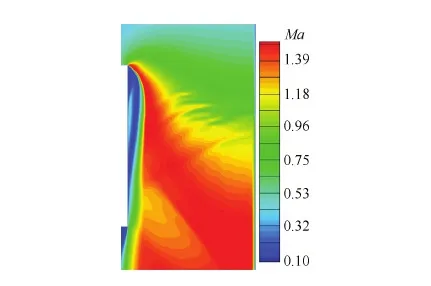
图19 0.8 mm间隙0.256 ms时刻流场马赫数分布 Fig.19 Mach number distribution at 0.256 ms in 0.8 mm leakage gap
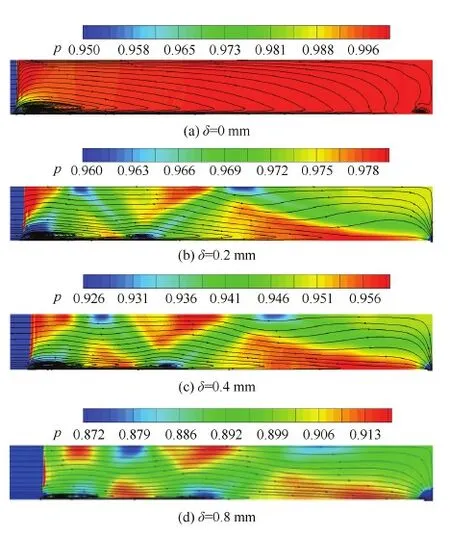
图20 0.336 ms间隙宽度变化时通道静压及流线分布 Fig.20 Static pressure and streamline distribution in channel with varying gap widths at 0.336 ms
进一步分析图20发现,随着间隙宽度增加,泄漏流量增大,激波波后平均压力下降,从而导致激波强度减弱,激波传播速度也随之降低。泄漏还导致了激波波后附面层分离形式的改变,除了由于逆压梯度在激波分岔脚形成的主分离泡,在膨胀波壁面反射引起的逆压梯度作用下又形成了新的次分离泡。
观察图21、图22,对于激波波后流场,随着泄漏过程的进行,同一位置不同时刻压力均值不变,不同位置时均压力相同。流场平均压力保持不变,这是非定常泄漏过程的典型流动特征。

图21 不同泄漏间隙宽度P4测点压力随时间变化 Fig.21 Pressure variation with time at P4 test point with varying leakage gap widths
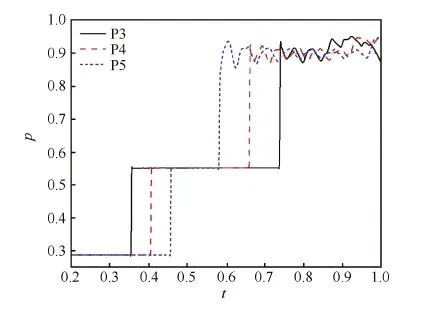
图22 间隙0.8 mm算例通道中心截面不同监测点压力变化曲线 Fig.22 Pressure curves of different monitor points at centerline of channel for case with 0.8 mm gap width
对比分析不含通道激波的非定常泄漏过程发现,无论是否存在通道激波,通道内均存在周期性的压力波动,这说明两者具有类似的压力波动机制,不同的是,通道内的主膨胀波被一道反射激波所取代。
4.2 泄漏对激波波速和激波强度的影响
激波波速和激波强度是波转子重要设计参数,考察泄漏对它们的影响具有重要意义。
图23给出了间隙宽度0 mm、0.8 mm 2个算例通道中心截面不同时刻的静压分布,图中x为沿通道方向坐标。可以看出,无论是否存在泄漏,激波运行轨迹均为直线,这说明在泄漏初始时刻激波波速已经下降到特定值,在激波传播过程中波速并不随着泄漏的发生而改变。因此对于给定的间隙宽度,激波马赫数不变。
图24给出了泄漏间隙进出口条件相同时激波绝对马赫数随无量纲间隙宽度δ/H的变化,两者近似为线性关系,δ/H=0.08时,激波绝对马赫数相比零间隙工况衰减了7.3%。虽然激波波后压力出现波动,但压力均值基本不变,选择激波通过测点后3个完整的波动周期对压力进行时均运算,得到激波静增压比随无量纲间隙宽度的变化关系,如图25所示,两者呈线性关系,δ/H=0.08 时,激波静增压比相比零间隙工况衰减了10.1%。

图23 间隙宽度0 mm、0.8 mm通道中心截面不同时刻静压分布 Fig.23 Distribution of static pressure at centerline of channel for gap widths being 0 mm and 0.8 mm at different times
对于理想正激波,激波静增压比与激波相对马赫数满足式(2)。根据数值计算结果可以得到通道内反射激波相对马赫数,进而由式(2)得到激波静增压比理论解;同样,由图21给出的反射激波波后压力波动曲线可以求出波后平均压力,将其与波前压力比值作为反射激波静增压比的数值解。图26给出了不同间隙宽度下数值解相对理论解的偏差,可以看到,所有算例偏差均在0.01以内,因此在分析性能参数时可以将存在泄漏时的通道反射激波视为一道理想正激波。
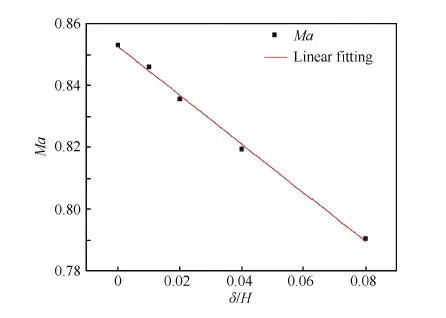
图24 反射激波绝对马赫数随泄漏无量纲泄漏间隙宽度变化 Fig.24 Absolute Mach number of reflected shock wave with non-dimensional leakage gap width
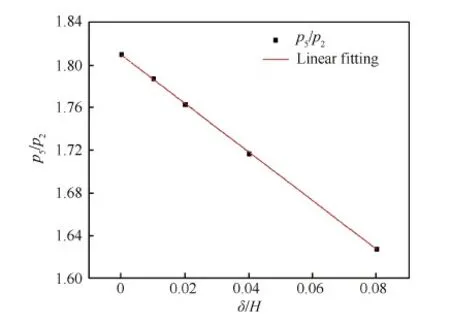
图25 反射激波静增压比随泄漏无量纲泄漏间隙宽度变化 Fig.25 Change of static pressure ratio of reflected shock wave with non-dimensional leakage gap widths
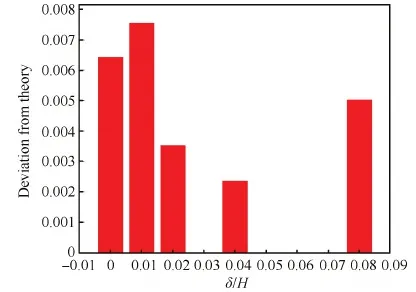
图26 反射激波静增压比计算结果相对理论偏差 Fig.26 Deviation of calculation results from theory for static pressure ratio of reflected shock wave
4.3 存在泄漏时的通道激波衰减机制
考察不同间隙宽度下通道内不含运动激波时的非定常泄漏过程,将主膨胀波通过给定测点后的压力做时均运算,进而得到时均压力相对通道初始压力的衰减幅值;同样,可以得到不同间隙宽度下反射激波波后时均压力相对零间隙宽度时的衰减幅值。
图27给出了上述2种情形的对比结果,其中p0为零间隙宽度时的通道初始压力,p为存在泄漏时的通道压力。可以看到,压力衰减幅值曲线几乎重合,这说明存在泄漏时通道激波的衰减本质上是泄漏产生的主膨胀波在通道内的传播引起的,存在泄漏时的通道激波可视为理想激波与泄漏引起的主膨胀波的线性叠加。
综上所述,泄漏流动通过泄漏引起的主膨胀波对激波传播施加影响,泄漏间隙宽度一定时,主膨胀波强度不变,因此通道激波的衰减幅值在传播过程中维持不变。
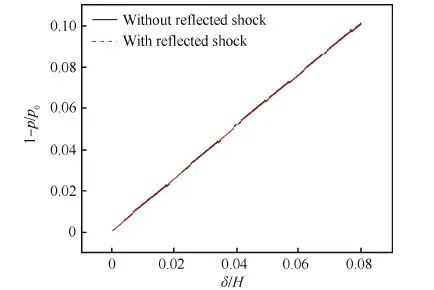
图27 有/无反射激波两种情形下不同间隙宽度通道内压力衰减幅值对比 Fig.27 Comparison of attenuation amplitude of channel pressure with different leakage gap widths with and without reflected shock
4.4 非定常泄漏损失预测模型
基于对通道激波衰减机制的认识,通过对不含通道激波时非定常泄漏过程进行模化,建立非定常泄漏损失预测模型。该模型主要基于以下几个重要假设:① 间隙泄漏流动等效为沿通道的均匀流动;② 膨胀波系简化为一道膨胀波;③ 以膨胀波波头、波尾平均速度代表简化后的膨胀波波速;④ 泄漏流动为等熵流动;⑤ 泄漏过程中膨胀波强度及波后气体参数均保持不变。
在上述假设基础上,最终得到无量纲泄漏间隙宽度G为
(4)

(5)
由于本文所有算例泄漏间隙均处于壅塞状态,即间隙上下游压力满足式(6),根据式(4),激波衰减幅值ep仅是无量纲间隙宽度G与流量系数C0的函数。根据CFD计算结果确定C0、ep,再由泄漏损失预测模型可求得G值,从而验证预测模型的可靠性。表2给出了预测模型数值验证结果,Gmodel为预测模型G值。可以看出,两者吻合良好。
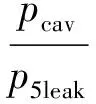
(6)
表2泄漏流动损失预测模型数值验证结果
Table2Numericalverificationresultsoflosspredictionmodelforleakageflow
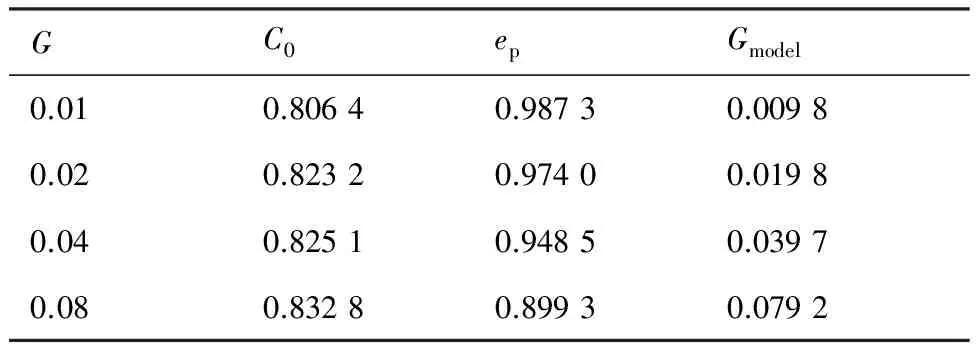
GC0epGmodel0.010.80640.98730.00980.020.82320.97400.01980.040.82510.94850.03970.080.83280.89930.0792
5 结 论
1) 阐明了非定常泄漏过程转子通道的压力波动机制,即连续反射膨胀波、周期性出现的弓形激波及其在通道中心截面的反射波引起了通道压力的周期性波动。
2) 阐明了间隙内部泄漏流动的3个发展阶段及其流动特征:① 通道激波的绕射、反射及传播;② 间隙出口非定常膨胀波的逆向传播及与间隙激波的非定常相互作用;③ 准稳态流动阶段。
3) 在泄漏过程中通道激波传播速度不变、波后时均压力不变。
4) 激波马赫数、激波静增压比与无量纲间隙宽度均呈线性关系,当间隙宽度从0增大到0.08时,激波马赫数衰减7.3%,激波静增压比衰减10.1%。
5) 泄漏引起的激波衰减本质上是主膨胀波与通道激波叠加效应的结果。
6) 本文给出的泄漏损失预测模型可以准确预测泄漏引起的激波衰减。
[1] WEBER H E. Shock wave engine design[M]. New York: John Wiley & Sons, Inc, 1995: 1-4.
[2] DEMPSEY E, MULLER N, AKBARI P, et al. Performance optimization of gas turbines utilizing four-port wave rotors: AIAA-2006-4152[R]. Reston: AIAA, 2006.
[3] AKBARI P, KHARAZI A A, MULLER N. Utilizing wave rotor technology to enhance the turbo compression in power and refrigeration cycles: IMECE-2003-44222[R]. New York: ASME, 2003.
[4] AKBARI P, NALIM R, MULLER N. A review of wave rotor technology and its applications: IMECE-2004-60082[R]. New York: ASME, 2004.
[5] KENTFIELD J A C. Nonsteady, one-dimensional, internal, compressible flows: theory and applications[M]. Oxford: Oxford University Press, 1993: 127-128.
[6] WILSON J. An experimental determination of losses in a three-port wave rotor[J]. Journal of Engineering for Gas Turbines and Power, 1998, 120(4): 833-842.
[7] PAXSON D E. Comparison between numerically modeled and experimentally measured wave-rotor loss mechanisms[J]. Journal of Propulsion and Power, 1995, 11(5): 908-914.
[8] AKBARI P, NALIM M R. Leakage assessment of pressure-exchange wave rotors[J]. Journal of Propulsion and Power, 2008, 24(4): 732-740.
[9] WILSON J, WELCH G E, PAXSON D E. Experimental results of performance tests on a four-port wave rotor: AIAA-2007-1250[R]. Reston: AIAA, 2007.
[10] ELEUTERIO F T. Riemann solvers and numerical methods for fluid dynamics[M]. Heidelberg: Springer, 2009: 115-119.
[11] GLASS I I, PATTERSON G N. A theoretical and experimental study of shock-tube flows[J]. Journal of the Aeronautical Sciences, 1955, 22(2): 73-100.
[12] ZHANG G, SETOGUCHI T, KIM H D. Numerical simulation of flow characteristics in micro shock tubes[J]. Journal of Thermal Science, 2015, 24(3): 246-253.
[13] OKAMOTO K, NAGASHIMA T. Visualization of wave rotor inner flow dynamics[J]. Journal of Propulsion and Power, 2007, 23(2): 292-300.
[14] ZHANG G, KIM H D. Numerical simulation of shock wave and contact surface propagation in micro shock tubes[J]. Journal of Mechanical Science and Technology, 2015, 29(4): 1689-1696.
[15] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 171.
YAN C. Methods and applications of computational fluid dynamics[M]. Beijing: Beihang University Press, 2006: 171 (in Chinese).
[16] SAITO T, TAKAYAMA K. Numerical simulations of nozzle starting process[J]. Shock Waves, 1999, 9(2): 73-79.
[17] DESHPANDE A, PURANIK B. Effect of viscosity and wall heat conduction on shock attenuation in narrow channels[J]. Shock Waves, 2015, 25(1): 1-11.
[18] SKEWS B W. The perturbed region behind a diffracting shock wave[J]. Journal of Fluid Mechanics, 1967, 29(4): 705-719.
[19] TAKAWAMA K, INOUE O. Shock wave diffraction over a 90 degree sharp corner-posters presented at 18thISSW[J]. Shock Waves, 1991, 1(4): 301-312.
[20] IGRA O, FALCOVITZ J, REICHENBACH H, et al. Experimental and numerical study of the interaction between a planar shock wave and a square cavity[J]. Journal of Fluid Mechanics, 1996, 313: 105-130.
(责任编辑: 张晗)
URL:www.cnki.net/kcms/detail/11.1929.V.20161010.1621.002.html
Mechanismofnonsteadyleakageflowofwaverotors
LIUChenyuan,LIUHuoxing*
SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083,China
Theproblemofleakageflowcanrestricttheperformanceofawaverotor.Thispaperextractsmainflowphenomenarelatedtoleakageinawaverotor,andestablishesatwo-dimensionalsinglepassageleakagemodel.Themechanismofnonsteadyleakageflowisanalyzednumerically,andthepredictionmodelforlossofunsteadyleakageflowisfurtherverified.Theresultsshowthatthereexistspressureoscillationofvaryingextentinrotorpassage,andtheoscillationamplitudeisrelatedtothegapwidth.Thecontinuousreflectedexpansionwave,periodicemergingbowshockanditsreflectedshockarereasonsforpressureoscillation.Thereexistthreemainflowstagesintheleakagegapduringleakageflowprocessandduringwhichthepropagationspeedofpassageshockandpost-shocktime-averagingpressurestayunchanged.Withinacertainrangeofgapwidth,shockMachnumberandshockstaticpressureratioarebothlinearlydependentonthenondimensionalleakagegapwidth.Whenthegapwidthisincreasedfrom0to0.08,theshockMachnumberdecreasesby7.3%,andtheshockstaticpressureratiodecreasesby10.1%.Thepropagationofchannelshockwaveisinfluencedbyleakageflowprocessviamainexpansionwave,andshockwaveattenuationisessentiallytheresultofsuperpositionofidealshockwaveandexpansionwave.TheresultsobtainedwithleakagelosspredictionmodelisfoundtobeconsistentwithCFDresults.
gasturbine;waverotor;singlepassagemodel;nonsteadyleakageflow;shockwave
2016-07-12;Revised2016-08-24;Accepted2016-10-08;Publishedonline2016-10-101621
.E-mailliuhuoxing@buaa.edu.cn
2016-07-12;退修日期2016-08-24;录用日期2016-10-08; < class="emphasis_bold">网络出版时间
时间:2016-10-101621
www.cnki.net/kcms/detail/11.1929.V.20161010.1621.002.html
.E-mailliuhuoxing@buaa.edu.cn
刘琛源, 刘火星. 波转子非定常泄漏流动机理J. 航空学报,2017,38(5):120606.LIUCY,LIUHX.Mechanismofnon-steadyleakageflowofwaverotorsJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120606.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0269
V231.3
A
1000-6893(2017)05-120606-14
