超低轨航天器气动特性快速预测的试验粒子Monte Carlo方法

靳旭红， 黄飞， 程晓丽， 王强

中国航天空气动力技术研究院， 北京 100074

超低轨航天器气动特性快速预测的试验粒子Monte Carlo方法

靳旭红， 黄飞*， 程晓丽， 王强

中国航天空气动力技术研究院， 北京 100074

超低轨(LEO)卫星气动特性的快速准确计算是对其进行轨道预测和控制的关键输入条件。基于真空技术领域中计算管道分子流率的试验粒子Monte Carlo (TPMC) 方法，结合自由分子流理论，发展了一套快速准确预测低轨卫星气动特性的TPMC方法，给出了其模拟步骤及主要关键技术点，并采用该方法模拟了带电池翼超低轨卫星的气动特性和航天器典型构件之间的多次反射效应。结果表明：TPMC方法在计算超低轨航天器气动力、力矩时具有较高的可靠性和对工程复杂外形的适用性；该方法能够准确模拟自由分子流理论无法求解的多次反射问题，给出正确的气动力系数；该方法的计算速度比直接模拟Monte Carlo (DSMC)快3～4个量级，存储量要求也比后者低1～2个量级，是超低轨航天器气动特性快速准确预测的一个理想方法。

低地球轨道； 卫星； 气动特性； 多次反射； 试验粒子Monte Carlo (TPMC)； 平板

距地面200～1 000 km的低地球轨道 (Low Earth Orbit, LEO) 环境，是对地观测卫星、气象卫星、通讯遥感卫星、载人飞船、空间站等大型复杂结构航天器的运行区域[1]。近年来，由于重力场和稳态海洋环流精确测量的需要，超低地球轨道 (200～500 km) 航天器逐渐展现出广阔的应用前景。欧洲空间局 (European Space Agency，ESA) 于21世纪初相继发射了GRACE (Gravity Recovery And Climate Experiment)、CHAMP (CHAllenging Mission Payload) 和GOCE (Gravity field and steady state Ocean Circulation Explorer) 卫星[2-4]。由于地球重力场信号随着高度的上升而快速衰减，以及当前卫星重力测量技术自身的局限性，此类卫星的高度不得不足够低，以最大化对地球重力场的敏感度[5]。正因为这个原因，上述3颗卫星的高度逐渐递减，GRACE和CHAMP的平均高度范围分别为400～500 km和350～400 km[6]，而GOCE卫星则运行在更低的低地球轨道——250～300 km。实现重力梯度精确测量的先决条件是给卫星提供一套无拖拽姿态控制(Drag-Free and Altitude Control, DFAC) 系统，该系统采用一套离子发动机和磁力矩器来补偿大气阻力、太阳光压和地球辐射反照压等非地球重力的影响，从而进行姿态控制[5]。在超低轨道环境下，尤其是200～300 km高度，太阳光压和地球辐射反照压比大气阻力小得多[7]，因此稀薄大气引起的气动阻力仍然是主要的控制问题。在低地球轨道大气环境条件下，阻力系数和大气密度是卫星阻力预测不确定度的最大来源[8]。为了实现快速的卫星姿态控制和精确的重力梯度测量，DFAC需要快速准确的阻力输入。所以，实现阻力系数的快速准确预测，是超低轨道卫星正常工作的前提条件。

在太空时代的早期，通过轨道分析从轨道衰减推演绝对大气密度时，大多采用2.2作为紧致形状卫星的阻力系数[9]。这是20世纪60年代Cook[10-11]基于实验室对清洁表面所受气动阻力的测量而给出的。而且，著名的美国标准大气(1976)和Jacchia系列大气模型就是采用该阻力系数并利用卫星轨道衰减数据构建起来的[12-13]。然而，在通过卫星轨道数据估算大气密度时，在不同高度使用固定值作为紧致卫星的阻力系数会引起较大的偏差。轨道高度为200 km时，根据美国标准大气(1976)，分子平均自由程为235.214 m，取卫星特征长度为5 m，则来流Knudsen数(Kn，定义为分子自由程与特征长度的比值)约为40，按照中国著名科学家钱学森[14]的划分，属于自由分子流区。随着稀薄气体动力学的发展，自由分子流理论能够给出平板、圆球和圆柱等简单几何外形卫星阻力系数的闭合形式的分析解[15-17]。然而，大部分卫星都具有复杂的外形，其阻力系数不再存在分析解。对于这类复杂几何外形的卫星，一般都采用面元积分法[18]计算其阻力系数。面元积分方法虽然比工程估算中直接取2.2作为阻力系数准确，但也忽略了卫星实体之间的遮挡和多次反射效应，尤其是对于由多个实体组成的卫星和具有凹形表面的卫星。直接模拟Monte Carlo (Direct Simulation Monte Carlo, DSMC) 方法[19-20]虽然具备准确模拟三维复杂稀薄流动的能力，却需要耗费巨大的计算时间和存储量[21]，在当前的计算机硬件条件下，高性能并行DSMC模拟也无法满足轨道分析的要求。

1960年，Davis[22]提出试验粒子Monte Carlo (Test Particle Monte Carlo, TPMC)方法，并成功用于计算通过分子平均自由程远大于圆管特征尺度条件下的圆管分子流率。该方法适用于Knudsen数趋于无穷大的无碰撞流动或者分子间碰撞相对于分子与壁面的碰撞影响很小的近自由分子流动。它区别于DSMC方法的明显特点是仿真分子是顺序而非同时产生的，一次只产生一个试验粒子，因此不会耗费太多的计算时间和存储量，更适用于复杂边界导致的多次表面反射流动问题[23]。美国学者Fan[24-25]、Guo[26]等已经将TPMC方法成功用于简单航天器表面出气导致的自散射和环境散射返回流污染问题，Skovorodko[27]基于Davis的TPMC方法发展了一套Holweck泵内部自由分子流动模拟的数值算法，该算法获得的结果与低压条件下的实验测量一致。Morozov等[28]采用TPMC方法对激光烧蚀材料的低强度蒸发过程进行了模拟，分析了蒸发粒子质量和背景气体压强对材料沉积速率的影响。Malyshev和Middleman[29]采用TPMC方法对非蒸发吸气剂 (Non-Evaluation Getter, NEG) 薄膜的黏附几率进行了准确模拟，研究气体喷射过程中压力读数的影响。Plotnikov和Shkarupa[30]基于泛函随机模拟算法理论，提出了一种构建渐进置信区间的方法，分析了TPMC方法的统计误差和最优化参数。本课题组前期[31-32]也开展了该方法在环境散射返回流污染方面的研究工作。以上对TPMC方法的研究都集中在真空技术、航天器环境工程和材料工程领域，特别地，据作者所知，国内尚无人实现TPMC方法在气动特性分析领域的应用。

鉴于TPMC方法能够兼顾面元积分法的计算效率和考虑复杂卫星构型存在的多次反射问题，本文基于真空技术领域提出的计算管道分子流率的TPMC方法，结合自由分子流理论，发展了一套快速准确地预测低轨卫星气动特性的TPMC方法。首先，详细给出了TPMC方法的模拟步骤及主要关键技术点；然后，以具有工程应用背景的带电池翼超低轨卫星为例验证了该方法在复杂外形上的适应性及可靠性；最后以存在多次反射现象的复杂航天器典型构件验证了该方法对多次反射问题快速准确的模拟能力。

1 试验粒子Monte Carlo方法

与DSMC方法一样，TPMC方法也是一种随机模拟方法，只是其忽略了分子之间的碰撞，因此只适用于无碰撞或者近自由分子流动。TPMC方法的基本思想是通过跟踪计算域内试验粒子的轨迹来模拟气体流动，假设一个试验粒子代表大量的真实气体分子，在计算机中模拟试验粒子的运动轨迹，并进行试验粒子与物体表面的碰撞，待试验粒子的采样数量足够大以保证真实物理过程的特征均得到准确模拟后，统计出气动力、热等空气动力学宏观量。

1.1 TPMC模拟过程

TPMC方法的主要模拟步骤如下：

1) 构建一个足够大的圆柱体计算域，航天器位于该计算域内部。

2) 根据自由来流条件在计算域边界产生试验粒子，对其初始位置和速度进行随机取样。

3) 根据步骤2)给出的试验粒子初始位置和速度，计算该试验粒子的运动轨迹。

4) 判断计算出的运动轨迹是否与航天器表面发生碰撞：如果没有发生碰撞，则认为该试验粒子直接飞出计算域，转到步骤2)；如果发生碰撞，继续执行步骤5)。

5) 按照指定的气体与表面相互作用模型(本文采用能量完全适应的漫反射模型)计算试验粒子与航天器表面碰撞后的速度，之后按照步骤3)继续跟踪该试验粒子。

6) 根据试验粒子与航天器表面的碰撞，计算单次碰撞的动量和能量交换，跟踪足够多的试验粒子后，统计空气动力学力学宏观量，从而得到低轨航天器的气动特性规律。

1.2 主要关键步骤

1.2.1 构建计算域

计算域为一个圆柱体，坐标系原点、低轨航天器几何中心和圆柱体几何中心重合，如图1所示。设Rref和Lref分别为航天器的特征半径和长度，则圆柱体计算域的半径Rc和长度Lc分别为

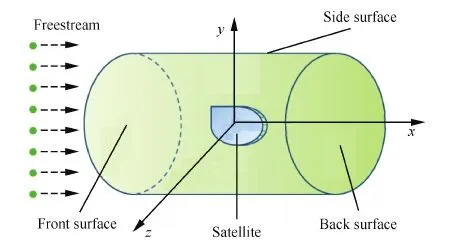
图1 圆柱体计算域和坐标系 Fig.1 Computational domain and coordinate system of cylinder

(1)

式中：K为足够大的正参数，从而使计算域尺寸足够大以保证可以忽略计算域外部气体的影响。

1.2.2 试验粒子初始位置取样

试验粒子初始位置取样的理论基础是其在圆柱体计算域表面均匀分布，可用概率分布函数求逆法确定[33]。假设试验粒子初始位置在图1所示的坐标系中表示为 (x,y,z)。由于计算域边界包括圆柱体前面、后面2个平面和圆柱体侧面1个柱面，故需要考虑以下3种情形。

1) 若试验粒子在计算域前边界面产生，则

(2)

式中：R1、R2和下文中的Ri(i∈N,i≥3)均为(0, 1)区间均匀分布的随机数。

2) 若试验粒子在计算域后边界面产生，则

(3)

3) 若试验粒子在计算域侧边界面产生，则

(4)

1.2.3 试验粒子初始速度取样

试验粒子初始速度c为来流速度c0和分子热运动速度c′的矢量和。热运动速度c′服从如下形式的Maxwell分布，即

(5)

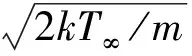
试验粒子在计算域的3个边界面产生。考虑进入某个面元的分子数通量，设某个计算域边界面面元的单位内法向量(指向计算域内部)和来流速度c0的夹角为φ。定义柱坐标系(x,r,θ)，它与图1所示的直角坐标系的转换关系为

(6)

令无量纲的热运动速度为

ξ=c′/cm

(7)

则试验粒子的初始速度为

c=c0+cmξ

(8)

设无量纲热运动速度ξ在式(6)所定义的柱坐标系中的分量为(ξx,ξr,ξθ)，根据分子动力学的相关结论进行推演，容易得到三维随机变量(ξx,ξr,ξθ)的联合概率密度函数为[34]

fin(ξx,ξr,ξθ)=

(9)

式中：来流速度比s定义为来流速度大小与最可几分子热运动速度的比值，即

s=|c0|/cm

(10)

(11)

式中：erf(t)为误差函数，即

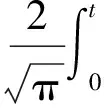
(12)

式中：η为积分变量。

3个分量的边际概率密度函数可以通过对联合概率密度函数在另外两个分量的取值范围进行积分[35]，即

(13)

利用文献[36]的概率积分公式，容易得出

(14)

对应概率分布函数为概率密度函数的积分[35]，即

结合以上分析可得，多相位分段调制干扰可以在真实目标周围形成一定范围的局部遮盖效果，且通过对干扰信号分段数、调制相位数以及调制相位值三个参数的控制可以实现灵活多样的干扰效果。

(15)

容易积分得三维随机变量ξx,ξr,ξθ的边际概率分布函数为

(16)

再次利用概率分布函数求逆法[33]，令

(17)

(18)

对于ξr和ξθ，直接利用随机数写出其表达式，即

(19)

对于第一个分量ξx，可以根据式(17)采用取舍法(Acceptance-rejection Method)[33]给出其随机取样。

至此，试验粒子的初始速度取样完全由式(8)、式(19)和取舍法给出。

1.3 力学宏观量统计

某表面气动力、力矩和热量的来源是入射分子在该表面的碰撞和反射，故其计算方法是对大量试验粒子和物体表面的动量与能量交换进行统计。某次气体分子与航天器表面碰撞时的动量与能量交换为

(20)

式中：ci为入射分子的速度矢量；cr为完全漫反射的分子速度矢量；Ei为入射分子的总能；Er为反射分子的总能。总能为平动能与内能(包括转动能和振动能)之和，其表达式分别为

(21)

式中：γ为气体比热比，空气(双原子分子)取值1.4；Tw为航天器表面温度。

设N为所有试验粒子与该表面碰撞的总次数，则作用在该表面的气动力、力矩以及单位时间传递到该表面的热量为

(22)

式中：rj、ΔPj和ΔEj分别为第j次碰撞时力矩参考点到碰撞位置的位移矢量、动量交换量和能量交换量；A为一个试验粒子代表的真实气体分子数，其表达式为

A=n∞Qf+Qs+Qb/Ntp

(23)

式中：n∞为来流分子数密度；Ntp为试验粒子总数；Qf、Qs和Qb分别为来流通过计算域前面、侧面和后面的分子数通量，其表达式为

(24)

2 带电池翼超低轨卫星气动特性

考察一个常见卫星的简化外形，即由1个长方体的卫星本体和2个太阳能电池翼组成的低轨航天器，如图 2所示。卫星本体的轴向(X轴方向)、展向(Y轴方向)和法向(Z轴方向)长度分别为2.25、1.72、2.2 m，2个电池板的长度、宽度和厚度分别为5.16、2.2、0.1 m，且对称地分布在卫星本体的两侧，电池板与卫星本体的间隙为0.5 m，与卫星底面的夹角为20°。体轴参考坐标系的原点位于卫星本体质心(也是整个航天器的质心)，方向如图 2所示。

图2 带太阳翼低轨卫星示意图 Fig.2 Schematic drawing of a low Earth orbit satellite with two solar panels

考虑200 km高度的超低地球轨道大气环境，来流密度、温度和平均分子质量采用美国标准大气 (1976年) 确定，气体比热比取为1.4，气体与航天器表面相互作用采用能量完全适应的漫反射模型，具体的来流和计算条件列于表1 中。

为了进行可靠性验证，采用课题组开发的一套非结构网格DSMC程序(其可靠性经过了多次实践的验证[37-38])计算了有限个状态。此外，还采用基于自由分子流理论的面元积分方法(FMFPI)进行了计算。

图3给出了低轨航天器阻力系数CD、升力系数CL和俯仰力矩系数Cm随迎角的变化，迎角的变化范围为α∈-10°,10°。需要注意的是，力矩参考点的坐标为迎风面的面心。随着迎角的增加，低轨航天器的阻力系数大致线性地增大，而俯仰力矩系数则先由一个正值(力矩方向为+Y方向)减小到0，然后再反向增大。而且，无论是阻力系数，还是俯仰力矩系数，TPMC、DSMC和FMFPI方法都符合得较好，这一方面验证了TPMC方法和程序的正确性，以及对复杂工程应用外形的适用性，另一方面则从数值计算的角度证明了200 km高度下忽略分子间碰撞的合理性。此外，还说明了该带电池翼卫星外形，多次反射效应比较微弱，对气动特性的影响可以忽略。

表1带电池翼超低轨卫星算例来流和计算条件

Table1FreestreamandcomputationalparametersofthecaseofasatellitewithtwosolarpanelsinLEO

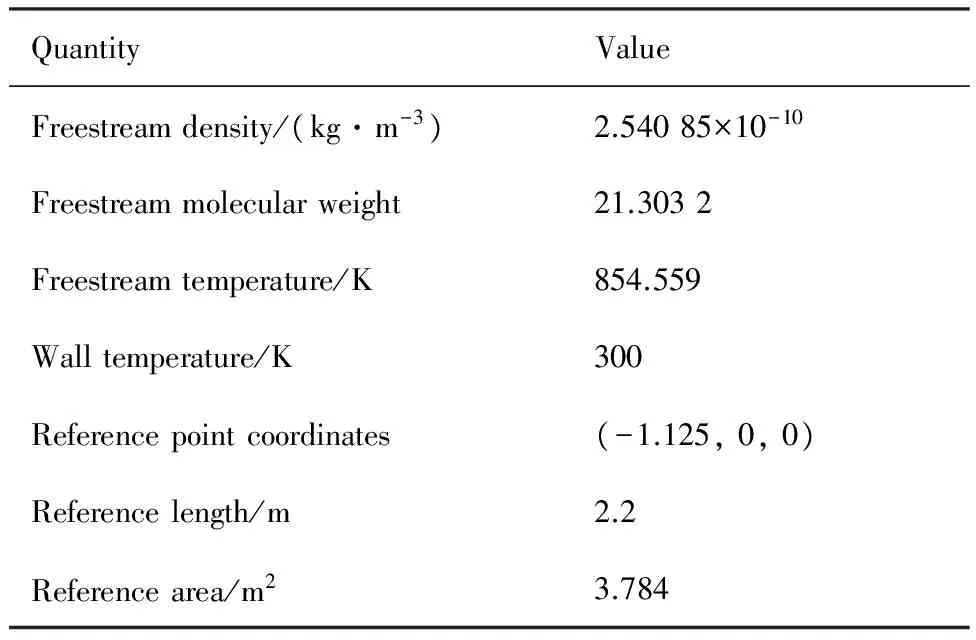
QuantityValueFreestreamdensity/(kg·m-3)2．54085×10-10Freestreammolecularweight21．3032Freestreamtemperature/K854．559Walltemperature/K300Referencepointcoordinates(-1．125，0，0)Referencelength/m2．2Referencearea/m23．784

图3 低轨卫星气动系数随来流迎角的变化 Fig.3 Variations of aerodynamic coefficients vs angles of attack in the case of a satellite in LEO

3 航天器典型构件多次反射效应

考虑航天器典型构件(比如航天飞机机身和机翼、机身和舵面)之间的多次反射效应，其简化模型为2个相互垂直的平板。2个平板的长度均为1 m，宽度均为0.5 m，厚度均为0.1 m，坐标系原点为2个平板垂直于厚度方向中心线的交点，如图 4所示，其中，左图为简化模型，右图为流动示意图和参考系。参考长度为1 m，参考面积为1 m2，力矩参考点为坐标原点，其他条件均和带电池翼卫星算例相同。

图4 简化航天器构件及其流动示意图 Fig.4 Simplified accessory on spacecraft and schematic drawing of a freestream over it

3.1 多次反射对气动特性的影响

考察垂直双平板阻力、升力系数随来流迎角的变化，迎角的变化范围为α∈[0°,90°]，即来流从平行于一个平板变化到垂直于该平板。如图5(a)所示，随着迎角的增加，阻力系数先增大后减小，在α=45° 处取得最大值，且阻力系数相对于迎角的变化曲线关于α=45°对称。对于升力系数，如图5(b)所示，α∈[0°,45°)时，升力系数取正值；α∈(45°,90°]时，升力系数取负值；α=45° 时，垂直双平板上下对称，故升力系数为0。需要注意的是，无论是阻力系数还是升力系数，TPMC模拟结果和DSMC都一致，但却与FMFPI方法存在差异，而这个差异恰好是多次反射效应的体现，因为FMFPI方法忽略了实体之间的多次反射效应，以下是详细的分析。

图5 航天器典型构件气动系数随来流迎角的变化 Fig.5 Variations of aerodynamic coefficients vs angles of attack in the case of a typical accessory on spacecraft

α=0° 时，来流平行于平板A而垂直于平板B，部分来流气体分子与平板B碰撞后会再次反射与平板A碰撞，这类二次碰撞的结果就是在平板A表面产生一个正的升力和负的阻力，故考虑了多次反射效应的TPMC和DSMC阻力计算结果比FMFPI低，而升力系数则为一个正值(若不考虑多次反射，0° 迎角对应的升力系数为0)。与0° 迎角的情形相类似，α=90° 时，来流垂直于平板A而平行于平板B，部分与平板A碰撞后的分子会反射再次与平板B相碰撞，这类二次碰撞的结果就是在平板B表面产生一个负的升力和负的阻力，所以TPMC和DSMC的阻力计算结果比FMFPI的低，升力系数则为一个负值(若不考虑多次反射，90° 迎角对应的升力系数为0)。α∈0°,45°时，第一类二次反射占主导地位，故TPMC和DSMC计算的升力系数比FMFPI的大；α∈45°,90°时，第二类二次反射占主导地位，故TPMC和DSMC计算的升力系数比FMFPI的小。在α=45° 附近，根据图 5(a)可知，该迎角区间内A、B两个平板之间多次反射的综合效果是使阻力轻微增大。这可以从两个方面进行解释：从数值方面来说，TPMC和DSMC模拟过程中考虑了多次反射，而FMFPI没有考虑多次反射，TPMC给出的阻力系数和DSMC一致，两者都比FMFPI的偏大，故多次反射的效果是使阻力增大；从流动物理现象上来看，迎角为45° 时，来流沿着垂直双平板的角平分面入射，在两个平板之间来回反射，由于边界条件为能量完全适应的漫反射，相对于单次入射就飞走的气体分子而言，经过多次反射之后的气体分子的速率大多比较小，损失的动量更多，产生的阻力更大，因此，多次反射的效果是使阻力增大。

以上分析表明，TPMC方法具备准确模拟复杂航天器实体之间多次反射效应的能力。

3.2 计算效率对比

表2定量地列出了TPMC和DSMC方法计算1个状态时所消耗的计算资源，TPMC和DSMC程序均在相同配置的工作站上运行，内存容量为32 GB，中央处理单元(CPU)主频均为2 GHz。其中，TPMC方法采用440个面网格单元进行计算，共产生并跟踪了107个试验粒子；DSMC采用16 954个体网格单元进行计算，仿真粒子数约847 700个，时间步长为10-5s，60万步开始采样，共采样120万步。显然，对于超低轨航天器气动特性问题而言，TPMC的效率显然比DSMC高很多，不考虑并行效率的情况下，前者的计算速度是后者的10 000余倍，消耗内存也比后者少1～2个两级。需要说明的是，TPMC方法的计算高效性是以忽略气体分子之间的碰撞作为代价的，因此，该方法只适用于自由分子流区(飞行高度200 km及以上)，对于过渡流区，DSMC模拟仍然是必不可少的。当然，DSMC计算所需要的时间与网格数量、仿真粒子数和采样步数有关，但上述计算条件是取得较好模拟结果(统计误差较小、收敛性较好)的一个较宽松的条件。

表2TPMC和DSMC方法的计算代价

Table2ComputationalexpensesofTPMCandDSMCmethods

MethodTPMCDSMCCPU148Physicalmemory/MB4．52048×34Time/s530．64025120345．84153

4 结 论

1) 本文发展的TPMC方法可用于超低轨(飞行高度为200 km及以上)航天器气动力、力矩的快速准确预测，进而为该类卫星的轨道预测、控制提供快速准确的气动力、力矩输入。

2) 对于带电池翼低轨卫星的气动力和力矩，TPMC、DSMC和基于自由分子流理论的面元积分等3种计算方法结果一致，验证了TPMC方法的可靠性和对工程问题的适用性，同时也是200 km 高度无碰撞流动(自由分子流动)假设正确性的一个佐证。

3) 垂直双平板模型作为航天器典型构件间多次反射的简化，TPMC方法能够正确预测其气动力，表明该方法具备准确模拟航天器复杂实体之间多次反射现象的能力。

4) 对于超低轨航天器气动特性的计算，TPMC方法的计算速度比DSMC快3～4个量级，存储量要求也比后者少1～2个量级，因此是该类航天器气动特性快速准确预测的一个理想方法。

[1] 李志辉， 吴俊林， 彭傲平， 等. 天宫飞行器低轨控空气动力特性一体化建模与计算研究[J]. 载人航天, 2015, 21(2): 106-114.

LI Z H, WU J L, PENG A P, et al. Unified modeling and calculation of aerodynamics characteristics during low-orbit flying control of the TG vehicle[J]. Manned Spaceflight, 2015, 21(2): 106-114 (in Chinese).

[2] TAPLEY B D, BETTADPUR S, RIES J C, et al. GRACE measurements of mass variability in the Earth system[J]. Science, 2004, 305(5683): 503-505.

[3] REIGBER C, LUEHR H, SCHWINTZER P. CHAMP mission status[J]. Advances in Space Research, 2002, 30(2): 129-134.

[4] RUMMEL R, YI W, STUMMER C. GOCE gravitational gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777-790.

[5] SECHI G, BUONOCORE M, COMETTO F, et al. In-flight results from the drag-free and attitude control of GOCE satellite[C]//18th IFAC World Congress, 2011: 733-741.

[6] KOPPENWALLNER G. Satellite aerodynamics and determination of thermospheric density and wind[C]//27th International Symposium on Rarefied Gas Dynamics, 2010: 1307-1312.

[7] CANUTO E. Drag-free and altitude control for the GOCE satellite[J]. Automatica, 2008, 44: 1766-1780.

[8] MEHTA M M, MCLAUGHLIN C A, SUTTON E K. Drag coefficient modeling for grace using direct simulation Monte Carlo[J]. Advances in Space Research, 2013, 52: 2035-2051.

[9] VALLADO D A. A critical assessment of satellite drag and atmospheric drag modeling: AIAA-2008-6442[R]. Reston: AIAA, 2008.

[10] COOK G E. Satellite drag coefficients[J]. Planetary and Space Science, 1965, 13: 929-946.

[11] COOK G E. Drag coefficients of spherical satellites[J]. Annales Geophysicae, 1966, 22: 53-64.

[12] MOE K. Density and composition of the lower thermosphere[J]. Journal of Geophysics Research, 1973, 78: 1633-1644.

[13] JACCHIA L G. Static diffusion models of the upper atmosphere: Special Report No. 170[R]. Cambridge, MA: Smithsonian Astrophysics Obs., 1964.

[14] TSIEN H S. Superaerodynamics, mechanics of rarefied gases[J]. Journal of Aeronautical Science, 1946, 13: 653-664.

[15] SCHAAF S A, CHAMBRE P L. Flow of rarefied gases[M]. Princeton: Princeton University Press, 1961: 687-708.

[16] SENTMAN L H. Free molecule flow theory and its application to the determination of aerodynamic forces: TR LMSC-448514[R]. Sunnyvale, CA: Lockheed Missile and Space Corporation, 1961: 265-409.

[17] SENTMAN L H. Comparison of the exact and approximate methods for predicting free-molecular aerodynamic coefficients[J]. American Rocket Society Journal, 1961, 31: 1576-1579.

[18] FULLER J D, TOLSON R H. Program for the estimation of spacecraft aerodynamic properties: AIAA-2009-0728[R]. Reston: AIAA, 2009.

[19] BIRD G A. Approach to translational equilibrium in a rigid sphere gas[J]. Physics of Fluids, 1963, 6: 1518-1519.

[20] BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York: Oxford University Press, 1994: 208-217.

[21] LEE J W, YI M Y. Modified view factor method for estimating molecular backscattering probability in space conditions[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(2): 336-341.

[22] DAVIS D H. Monte Carlo calculation of molecular flow rates through a cylindrical elbow and pipes of other shapes[J]. Journal of Applied Physics, 1960, 31(11): 69-76.

[23] BIRD G A. Monte Carlo simulation of gas flows[J]. Annual Review of Fluid Mechanics, 1978, 10(8): 11-31.

[24] FAN C, GEE C, FONG M C. Monte Carlo simulation of molecular flux on simple spacecraft surfaces due to self- and ambient-scatter of outgassing molecules: AIAA-1993-2867[R]. Reston: AIAA, 1993.

[25] FAN C, GEE C, FONG M C. Monte Carlo simulation for backscatter of outgassing molecules from simple spacecraft surfaces[J]. Journal of Spacecraft and Rocket, 1994, 31(4): 649-655.

[26] GUO K L, LIAW G S. Outgassing-ambient interaction of a spherical body: AIAA-1994-2063[R]. Reston: AIAA, 1994.

[27] SKOVORODKO P A. Free molecular flow in the Holweck pump[C]//22th International Symposium on Rarefied Gas Dynamics, 2000: 900-903.

[28] MOROZOV A A, GERETOVSZKY Z, SZORENYI T. Test particle Monte Carlo study of backward deposition during evaporation into a background gas[J]. Journal of Physics D: Applied Physics, 2008, 41: 1-6.

[29] MALYSHEV O B, MIDDLEMAN K J. Test Particle Monte-Carlo modelling of installations for NEG film pumping properties evaluation[J]. Vacuum, 2009, 83: 976-979.

[30] PLOTNIKOV M Y, SHKARUPA E V. Statistical error and optimal parameters of the test particle Monte Carlo method[C]//28th International Symposium on Rarefied Gas Dynamics, 2012: 880-886.

[31] 靳旭红, 黄飞, 程晓丽, 等. 圆盘表面出气环境散射返回流TPMC模拟[J]. 空气动力学学报, 2015, 33(5): 793-798.

JIN X H, HUANG F, CHENG X L, et al. Test particle Monte Carlo simulation for return flux due to ambient scatter of outgassing molecules on a circular disk[J]. Acta Aerodynamica Sinica, 2015, 33(6): 793-798 (in Chinese).

[32] 靳旭红, 黄飞, 程晓丽, 等. 航天器表面环境散射返回流TPMC模拟[J]. 计算物理, 2015, 32(5): 529-536.

JIN X H, HUANG F, CHENG X L, et al. Test particle Monte Carlo simulation of return flux on spacecraft surfaces due to ambient scatter of outgassing molecules[J]. Chinese Journal of Computational Physics, 2015, 32(5): 529-536 (in Chinese).

[33] BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York: Oxford University Press, 1994: 423-328.

[34] HORTON B E, BOWHILL S A. Computer simulation of supersonic rarefied gas flow in the transition region about a spherical probe: A Monte Carlo approach with application to Rocket-Borne ion probe experiments: NASA-CR-123315[R]. Washington, D.C.: NASA, 1971.

[35] 茆诗松, 程依明, 濮小龙. 概率论与数理统计教程[M]. 北京: 高等教育出版社, 2011: 139-161.

MAO S S, CHENG Y M, PU X L. A study for probability and statistics[M]. Beijing: Higher Education Press, 2011: 139-161 (in Chinese).

[36] BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York: Oxford University Press, 1994: 417-422.

[37] 黄飞， 沈清， 程晓丽， 等. 一种DSMC分子仿真下的权因子预定义方法[J]. 航空学报, 2014, 35(8): 2174-2181

HUANG F, SHEN Q, CHENG X L， et al. A new predefined method of particle weight in DSMC molecular simulation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2174-2181 (in Chinese).

[38] 黄飞， 苗文博， 程晓丽， 等. 一种DSMC仿真的并行策略[J]. 航空学报, 2014, 35(4): 968-974.

HUANG F, MIAO W B, CHENG X L, et al. A parallel algorithm of DSMC method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 968-974 (in Chinese).

(责任编辑： 李明敏)

URL：www.cnki.net/kcms/detail/11.1929.V.20161009.1006.006.html

TestparticleMonteCarlomethodforrapidpredictionofaerodynamicpropertiesofspacecraftinlowerLEO

JINXuhong,HUANGFei*,CHENGXiaoli,WANGQiang

ChinaAcademyofAerospaceAerodynamics,Beijing100074,China

FastandaccuratepredictionofaerodynamicpropertiesofsatellitesinlowerlowEarthorbit(LEO)isafundamentalprerequisitefordeterminationandcontroloftheorbit.BasedonthetestparticleMonteCarlo(TPMC)methodforthecalculationofmolecularfluxratethroughapipeinvacuumtechnology,theTPMCmethodforfastandaccuratepredictionofaerodynamicpropertiesofspacecraftinlowerLEOisdeveloped,combinedwiththefree-moleculartheory.Themainsimulationprocessesandimportantproceduresarepresented.ThemethodisvalidatedbycomparingtheaerodynamicpropertiesofasatellitewithtwosolarpanelswiththeresultsfromthedirectsimulationMonteCarlo(DSMC)techniqueandthepanelintegralmethodbasedonfree-molecularflowtheory.ItisindicatedthattheTPMCmethodisapplicabletocomplexconfigurationsinengineering.ResultsalsoshowsthattheTPMCmethodiscapableofdealingwithmultiplereflectionsthatthepanelintegralmethodcannotconsider,resultinginanaccurateaerodynamiccoefficient.Inaddition,theCPUtimeandphysicalmemoryusedbytheTPMCmethodislessthanthatbytheDSMCtechniquebyanorderof3to4and1to2,respectively,withoutcompromisingthesolutionaccuracy.TheTPMCisfoundtobeanidealmethodforfastandaccuratepredictionofaerodynamicpropertiesofsatellitesinlowerLEO.

lowEarthorbit;satellite;aerodynamicproperties;multiplereflections;testparticleMonteCarlo(TPMC);plate

2016-07-19；Revised2016-09-12；Accepted2016-09-22；Publishedonline2016-10-091006

.E-mailhuang05013@163.com

2016-07-19；退修日期2016-09-12；录用日期2016-09-22； < class="emphasis_bold">网络出版时间

时间：2016-10-091006

www.cnki.net/kcms/detail/11.1929.V.20161009.1006.006.html

.E-mailhuang05013@163.com

靳旭红， 黄飞， 程晓丽， 等． 超低轨航天器气动特性快速预测的试验粒子MonteCarlo方法J． 航空学报,2017,38(5):120625.JINXH,HUANGF,CHENGXL,etal.TestparticleMonteCarlomethodforrapidpredictionofaerodynamicpropertiesofspacecraftinlowerLEOJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120625.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0260

V411.3; O356

A

1000-6893(2017)05-120625-10