铝蜂窝芯弹性参数的有限元仿真计算

孙林峰，王冰松

（中车青岛四方机车车辆股份有限公司，山东 青岛266111）

铝蜂窝芯弹性参数的有限元仿真计算

孙林峰，王冰松

（中车青岛四方机车车辆股份有限公司，山东 青岛266111）

根据动车组铝蜂窝地板芯子的结构周期性，建立了求解其弹性参数的胞元模型，在有限元CAE软件ABAQUS环境下得到了三方向弹性模量的数值结果。通过与试验及解析结果的对比表明，该模型的计算精度较好。

蜂窝芯；弹性模量；ABAQUS

作为一类特殊的复合材料，铝蜂窝夹层板具有重量轻、刚度大、强度高等特点，已广泛应用在动车组内装件中。因此，对其力学性能的计算分析便成为一个重要的课题。对于呈六边形的铝蜂窝芯子单元，其与水平方向呈θ角的4条边长为l，厚度为t，竖直方向的2条边长为h，厚度为2t，如图1所示。

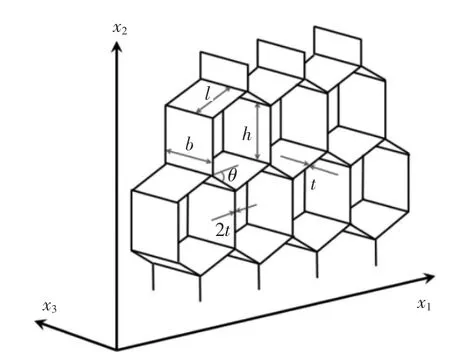
图1 铝蜂窝芯的结构尺寸

对于铝蜂窝芯弹性性能的计算，主要分为以Gibson[1]为代表的能量法、以Grediac[2]为代表的有限元法、以Nast[3]为代表的实验法和以Shi[4]为代表的均匀化理论。本文使用考虑了蜂窝孔壁弯曲、剪切及伸缩影响的解析公式[5]，给出某型铝蜂窝芯弹性模量的解析解。使用有限元法，在ABAQUS环境中建立起能够表征蜂窝周期性结构的胞元模型，通过限定合理的边界条件得到弹性模量的数值解。最后结合试验数据，将解析、数值和试验结果的吻合度进行对比，验证有限元模型的准确性。

1 数学模型的建立

在本文中使用Timoshenko理论和材料的小变形弹性假设，且认为胶接完好。对于动车组中常用的蜂窝芯，其壁厚与壁长的比值均可认为足够小。

1.1 E1的解析公式

如图2所示，首先考虑x1方向的单轴压缩，远端应力σ1使得蜂窝斜孔壁同时发生了弯曲、剪切和伸缩变形。根据力平衡条件及Timoshenko理论，可以得到力矩 M1、力 P 以及 x1、x2方向上的总挠度 δ11和 δ12，即

图2 蜂窝共面尺寸及1方向单轴受压变形

其中δ1为斜孔壁弯曲挠度，δs为斜孔壁剪切挠度，δa为斜孔壁轴向挠度。所以，x1方向上的单轴压缩条件下总应变 ε11、ε12为：

设基体铝材的弹性模量为Es，泊松比为vs，则可知x1方向上的弹性模量E1为：

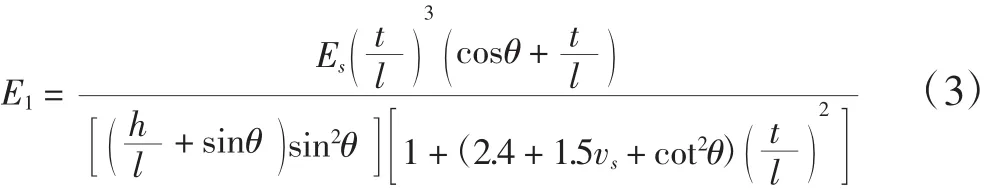
1.2 E2的解析公式

接着考虑x2方向的单轴压缩如图3所示，与前文推导方式类似，可以得到力矩M2、力W以及x1、x2方向上的总挠度 δ21和 δ22，即

图3 蜂窝共面尺寸及2方向单轴受压变形

其中δ2为斜孔壁弯曲挠度，δs为斜孔壁剪切挠度，δa-i为斜孔壁轴向挠度，δa-u为竖直孔壁轴向挠度。所以，x2方向上的单轴压缩条件下总应变ε21、ε22为：

同理，x2方向上的弹性模量E2为：

1.3 E3的解析公式

对于铝蜂窝芯的异面弹性模量E3，其值仅与等效前后的密度相关，即

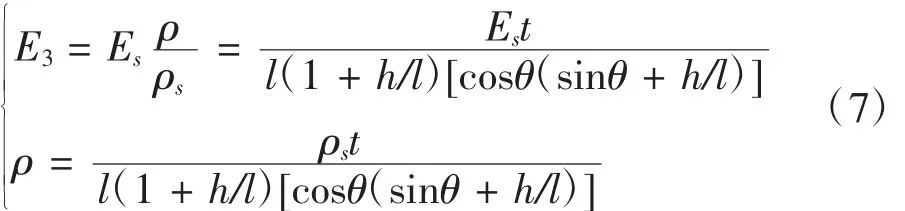
其中，ρs为基体铝材的密度，ρ为铝蜂窝芯的等效密度。

2 胞元法数值模型的建立

根据铝蜂窝芯的周期型结构，本文使用特征胞元代表整体结构进行有限元分析。

如图4所示，胞元深度与原结构一致，即为b，长度 L=8（lcosθ+t），高度 H=4（lsinθ+h）.在 ABAQUS中使用S4R壳单元进行网格划分，并注意孔壁厚度的不同。

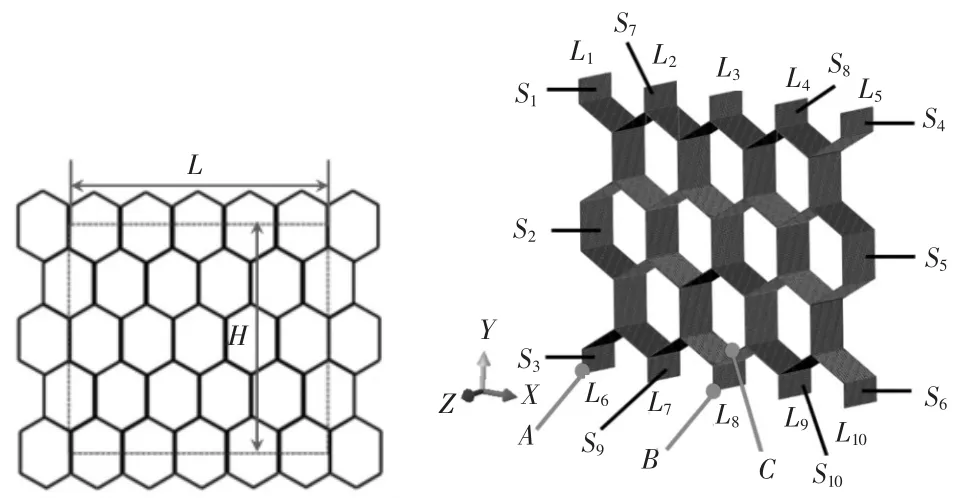
图4 特征胞元的选取及特征

对胞元模型分别施加如表1、表2和表3中所示的边界条件。需要注意的是，该边界条件需保证变形协调，即相对面上的节点间位移耦合。根据所提供的铝蜂窝芯样品[5]，胞元建模所需的尺寸及材料参数如表4所示。

表1 E1数值求解的边界条件

表2 E2数值求解的边界条件

表3 数值求解的边界条件

表4 尺寸及材料参数

3 弹性模量的数值结果

如图5至图7所示，胞元在共、异面方向上的变形结果满足位移耦合要求。对于x1变形，提取面S4、S5、S6上所有节点在x1方向上的节点力并求和得到ΣRF1；对于 x2变形，提取线 L1～L5上所有节点在 x2方向上的节点力并求和得到ΣRF2，对于x3变形，提取受载线上所有节点在方向上的节点力并求和得到ΣRF3.

图5 x1方向变形前后对比

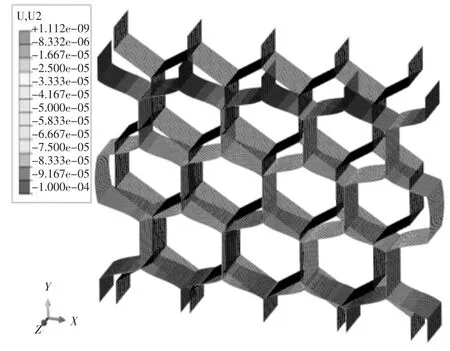
图6 x2方向变形前后对比

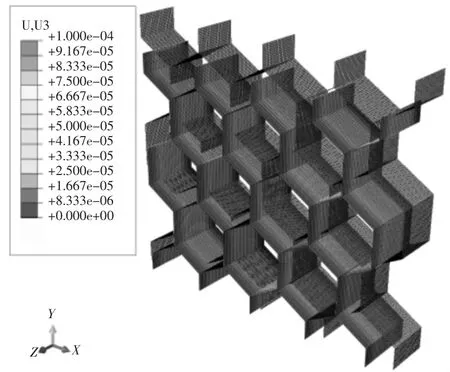
图7 x3方向变形前后对比

接着代入（7）式便可得到E1至E3的数值解：

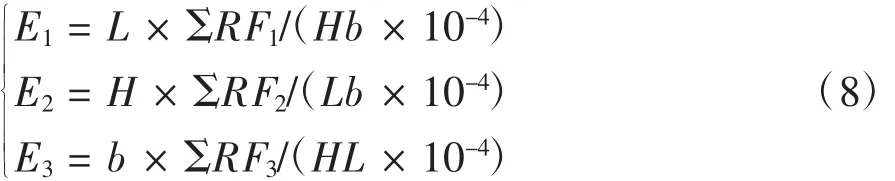
参照试验结果[5]，将式（3）、（6）和（7）得到的解析解、式（8）得到的数值解相比较，如表5所示。通过对比发现，胞元模型得到的弹性模量值与解析及试验解相比，一致性程度较高，且更贴近于试验值，证明所建立的胞元模型良好的计算准确性。

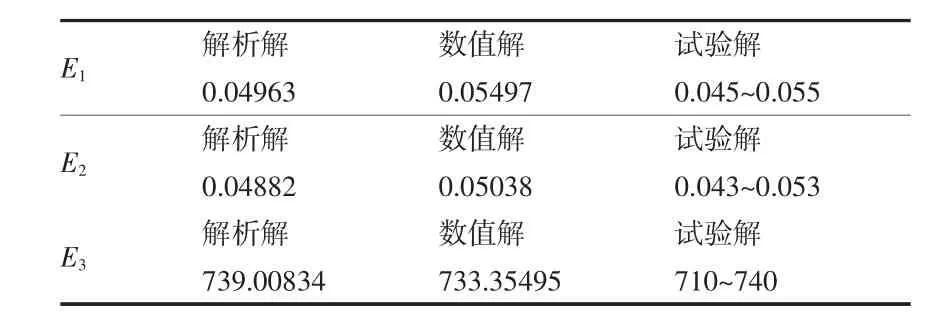
表5 弹性模量计算值对比（单位：MPa）

4 结论

本文通过合理选择胞元尺寸以及保证变形协调条件的边界约束条件，建立了能够快速计算动车组铝蜂窝地板芯子结构共异面弹性模量的有限元模型。通过与试验及解析结果对比发现，模型计算精度较好，能够为设计人员对蜂窝结构的相关优化工作提供数值基础。

[1]Lorna J.Gibson，Michanel F.Ashby.Cellular Solids：Struc ture and Properties[M].Oxford：pergamon，1988.

[2]Guo X，Gibson L.Behavior of intact and damaged honey comb：A finite-element study.Int J Mech Sci[J].1999，41（11）：85-105.

[3]Nast E.On honeycomb-type core moduli.AIAA/ASME/AS CE/AHS/ASC Structures，Structural Dynamics，and MaterialsConferenceandExhibit， 38th， andAIAA/ASME/AHS Adaptive Structures Forum[C].Kissimmee，FL，Apr.7-10，1997，1035-1044.

[4]Shi G，Tong P.Equivalent transverse shear stiffness of hon eycomb structure[J].Composite Structures，2006，19（3）：177-183.

[5]孙德强，张卫红，孙玉瑾.蜂窝铝芯的弹性模量和材料效率分析[J].力学与实践，2008，30（1）：35-40.

Finite Element Analysis on Honeycomb Core Elastic Constants

SUN Lin-feng，WANG Bing-song
（CRRC Qingdao Sifang Co.，Ltd.，Qingdao Shandong 266111，China）

According to the structural periodic property of EMU’s aluminum honeycomb floor，cell model for calculating the elastic constants had been established.Results of elastic modulus on three orthogonal directions were

in the CAE FE environment of ABAQUS.By data comparison of experimental，simulation and analytical outputs，the accuracy of the simulation model had been verified.

honeycomb core；elastic modulus；ABAQUS

U271.91

A

1672-545X（2017）09-0018-03

2017-06-07

孙林峰（1987－），男，河北廊坊人，工程师，硕士，研究方向：动车组内饰结构强度。