改编代数与几何综合题的实践与思考

黄曦明

（湖北省襄阳市第七中学）

改编代数与几何综合题的实践与思考

黄曦明

（湖北省襄阳市第七中学）

代数与几何综合题是初中数学中覆盖面最广，综合性最强的题型.常以函数为背景，结合几何图形，探讨存在性问题，体现分类讨论思想.数学试题千千万，那么我们有没有必要每道题都做一遍呢？该怎样突破这类难题呢？改编典型题打通知识间的联系是很好的策略.

存在性问题；改编综合题；复习效率

在初中数学总复习时，教师常常感觉这道题也好，那道题也很不错，尤其是面对全国各地区的中考试卷中的综合题，都想让学生做一做.但是，在有限的时间内，各学科的时间都很紧，不但学生没时间做，而且教师也来不及讲，究其原因还是没跳出题海战术的怪圈，就题论题，没有充分整合现有资源，打通知识间的联系，做到举一反三、融会贯通.本文以抛物线为背景的综合题为例，谈谈如何改编综合题，提高复习效率.

一、典型案例

题目（2016年山东·枣庄卷）如图1，已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1，且经过A(1,0)，C(0,3)两点，与x轴的另一个交点为点B.

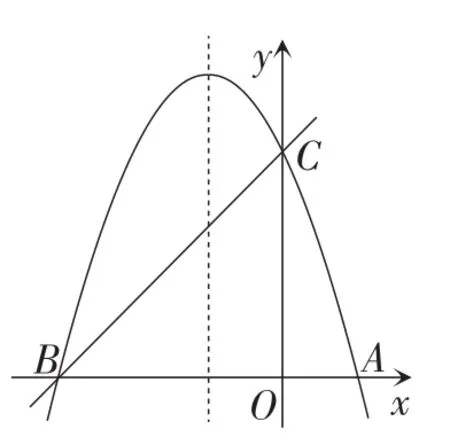
图1

（1）若直线y=mx+n经过B，C两点，求直线BC和抛物线的解析式；

（2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标；

（3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．

解：（1）已知抛物线y＝ax2＋bx＋c的对称轴为直线x=-1，且经过A(1,0)，C(0,3)两点，

所以抛物线的解析式为y=-x2-2x+3.

根据抛物线的对称性和点A的坐标A()1,0可求得点B的坐标为B()-3,0.

用待定系数法可求得直线BC的解析式为y=x+3．

（2）因为MA=MB，

所以MA+MC=MB+MC.

所以使MA+MC的值最小的点M应为直线BC与对称轴x=-1的交点.

把x=-1代入y=x+3，得y=2.

所以点M的坐标为M()-1,2，

即当点M到点A的距离与到点C的距离之和最小时点M的坐标为M()-1,2.

（3）设P(-1,t).

因为B(-3,0)，C(0,3)，

所以BC2=18，PB2=(-1+3)2+t2=4+t2，PC2=(-1)2+(t-3)2=t2-6t+10.

即18+4+t2=t2-6t+10.

解得t=-2.

②若点C为直角顶点，则BC2+PC2=PB2，

即18+t2-6t+10=4+t2.解得t=4.

③若点P为直角顶点，则PB2+PC2=BC2，

即4+t2+t2-6t+10=18.

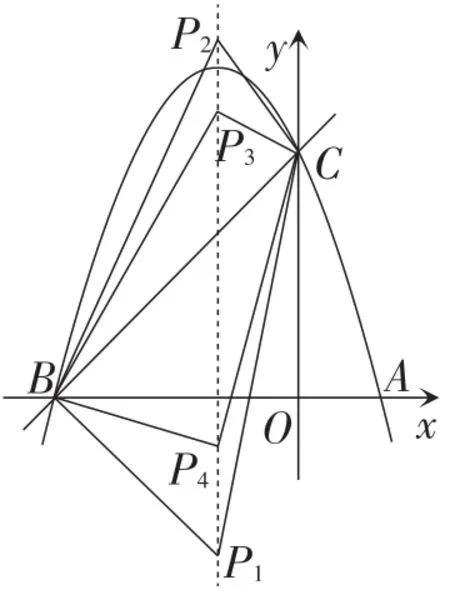
图2

【评析】此题考查了用待定系数法求函数的解析式、轴对称的性质、勾股定理及其逆定理、分类讨论的思想、解方程等知识点，是一道具有典型性和代表性的好题.试题设计容易入手，计算量不是很大，基础性很强，是很好的素材.从解法上来说，第（1）小题求二次函数的解析式还可设成顶点式y=a(x+1)2+k，然后将A(1,0)   ，C(0,3)两点的坐标代入求出a，k的值，或者根据对称轴得出抛物线与x轴交点B的坐标为B(-3,0)，然后把A，B，C三点的坐标代入y=ax2+bx+c(a≠0)求出a，b，c的值；由于此抛物线顶点及与坐标轴的交点坐标都是整数，便于计算，所以经常出现.此抛物线关于x轴、y轴对称的抛物线y=x2+2x-3和y=-x2+2x+3也经常出现.第（2）小题“使点M到点A的距离与到点C的距离之和最小”还可换个问法“使△MAC的周长最小”.第（3）小题除了用勾股定理解，还可以用相似三角形或三角函数来解.同时，抓住△BOC是等腰直角三角形这个隐藏的结论很容易求出点B或点C为直角顶点时，点P的坐标.所以在解法上要提倡一题多解，解法优化，这样才能发散思维，不要把学生的思维限制在一个狭窄的通道里，一定要注意解法的优化.

如果教师按照上面的解法讲解就题论题，并就此打住，而不进行二次开发，深入挖掘，那么这么好的资源就白白浪费，实在是令人惋惜.正如美国著名数学家波利亚曾说过，一个专心的认真备课的教师能够拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的理论领域.所以要以此题作为母题进行改编、变式，衍生出若干个子题来发挥它更大的价值.

二、改编的实践

代数与几何综合题要突出代数与几何图形的数形结合，知识的整合，本质是用代数的手段去量化几何问题，可通过改变设问的角度，改变已知条件，让图形动起来.同时，要渗透数学思想方法，较好地反映出学生分析问题和解决问题的能力.为改编方便，设题目中的抛物线的顶点为点D，E是对称轴与x轴的交点.

声乐演员在表演时调整好自己的心理状态是非常重要的。表演的时候不能够紧张和焦虑，这样会影响自己的正常发挥。在台上表演的时候要进入一种极佳的精神状态，就好像置身于故事之中，自己就是故事的主角，专心进行表演，才能真实表达出其中的情感。此外，要注意上场时的动作要潇洒自如，不要扭扭捏捏，给观众留下美好的“第一印象”，在表演的过程中，从头到尾都要表现得自然，保持良好的台风，全身心投入。

1.移动点的位置

第（3）小题属于典型的“两定+一动”构造特殊三角形问题，动点P还可设计在坐标轴上或者抛物线上，题目可设计成如下两个问题.

（1）设点P为抛物线上的一个动点，求使△BPC为直角三角形的点P的坐标；

（2）设点P为x轴上的一个动点，求使△BPC为直角三角形的点P的坐标．

2.增加动点的个数

再增加一个动点，变成“两定+两动”构造平行四边形问题，题目可设计成如下三个问题.

（1）若点F在抛物线的对称轴上，抛物线上是否存在点G，使以A，B，F，G四点为顶点的四边形为平行四边形？若存在，直接写出出所有满足条件的点G的坐标；若不存在，说明理由．

（2）若点H在x轴上，点P在抛物线上．是否存在以A，C，H，P四点为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，说明理由．

（3）如图3，F是抛物线对称轴上一点，且tan∠BFE=点H是x轴上的一个动点，过点H作HQ∥OF交抛物线于点Q，是否存在以点O，F，H，Q四点为顶点的平行四边形？若存在，求出点P的坐标；若不存在，说明理由.

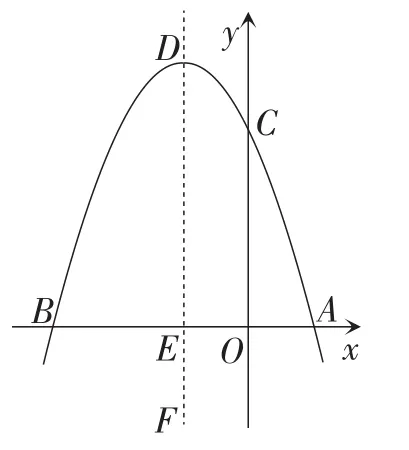
图3

3.改变三角形的形状

若将三角形的形状由直角三角形改为等腰三角形再继续探究，题目可设计成如下三个问题.

（1）在对称轴上是否存在点P，使△BPC为等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由.

（2）在对称轴上是否存在点P，使△CEP为等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由.

（3）问在y轴上是否存在点M，使得△BDM是直角三角形？若存在，直接写出点M的坐标；若不存在，说明理由．

4.探究三角形关系

若改成与已知三角形相似的问题，题目可设计成如下四个问题.

（1）判断△CDB的形状，并说明理由；△CDB与△ACO相似吗？为什么？

（2）在线段BC上是否存在点M，使△BOM∽△BAC？若存在，求出点M的坐标；若不存在，说明理由.

（3）探究坐标轴上是否存在点P，使得以点P，A，C四点为顶点的三角形与△BCD相似？若存在，直接写出点P的坐标；若不存在，说明理由.

（4）若线段BD上有一点P，使∠DCP=∠BDE，求点P的坐标．

5.计算图形的面积

如图4，P是抛物线上位于直线BC上方的一个动点，过点P作PH⊥Ox于点H，交线段BC于点Q，可设计成如下五个问题.

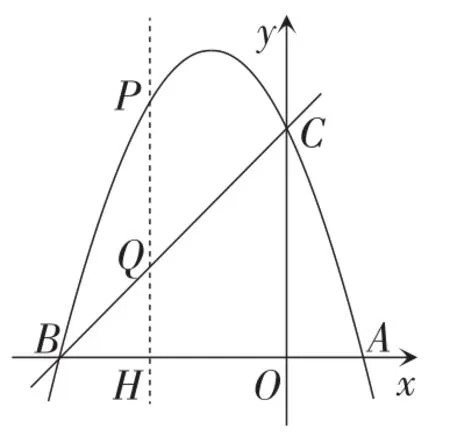
图4

（1）若S△BOP=4S△AOC，求点P的坐标；

（2）若直线BC把△PCH分成面积之比为2∶3的两部分，求出点P的坐标；

（3）求线段PQ长度的最大值．

（4）求△BPC的面积的最大值，并求出此时点P的坐标；

（5）求四边形BOCP面积的最大值，并求此时点P的坐标．

三、几点思考

1.教师要勤做题，多做题，练就过硬的基本功

教师要大量研究全国各地区的中考试题，探析试题，把握规律.虽然历年的中考试题从表面来看都是全新的，但仔细研究会发现它们之间有一定的延续性和相通性，可谓一脉相承，万变不离其宗.只有练就了深厚的数学功底，才能够循序渐进变式，将知识点进行嫁接迁移，打通知识间的联系，起到举一反三、融会贯通的作用.前面的改编思路实际上是笔者在研究全国各地区部分中考试题的基础上设计出来的.

经过教师的深加工，把问题设计成问题串而关联起来，让典型题焕发二次生命力.虽然教师辛苦了，但学生学的轻松了，而且大量重复的题没有必要做那么多，只需一题就能起到以一当十的效果，学生的时间自然够用了，复习效果立竿见影.

2.多媒体辅助教学

课堂上要完成大容量的问题，必须先制成试卷的形式前一天晚上发给学生先做，教师要精心制作配套的课件，如ppt、几何画板软件等，建议用几何画板软件制作课件，一是可动态演示，二是精准作图，三是随时度量，这样课堂才具有可操作性.如果学生基础薄弱，那就用两课时来完成.

3.变式的时机与侧重

根据班上学生的学情，改编要有所侧重.题目不宜太多、太乱，要由易到难，梯度推进，使学生对问题的认识逐步深化，不要为了变式而变式，否则重、难点不突出.例如，前面在计算图形的面积中第（3）（4）（5）小题从本质上来说是一回事，只是在设问时，换了个说法，属于一类题.

中考总复习内容多，时间紧，全国各地每年都有几百套试题，要想把其中的好题都做一遍，那是做不完的，很容易陷入题海战术的泥潭.从上面的改编变式可以看出，其实完全没有必要做那么多同类型的题，只需要在典型题的基础上进行改编变式，就可以将知识点打通，将知识点串起来，教师重点在解决这类题的思想和方法上予以指导，同时注意解题后的反思，提炼方法，总结经验，这样就可以将学生从题海中解脱出来，学得灵活，学得扎实，达到举一反三、触类旁通的效果，优化了的题组设计，自然就提高了复习效率.

［1］罗增儒.成题改编——移植转换［J］.中等数学，2005（10）：14-18.

［2］周著会.数学试题改编的几种策略［J］.数学通讯，2013（1）：27-29.

2017—07—12

黄曦明（1971—），男，中学一级教师，主要从事中学数学试题和教学研究.