多室鱼腹式箱梁剪滞效应分析*
2017-11-14金玉佳沈阳建筑大学交通工程学院沈阳110168
张 海, 金玉佳(沈阳建筑大学 交通工程学院, 沈阳 110168)
多室鱼腹式箱梁剪滞效应分析*
张 海, 金玉佳
(沈阳建筑大学 交通工程学院, 沈阳 110168)
针对鱼腹式箱梁应力及剪滞效应分布状态与传统箱梁不同的问题,通过使用有限元软件进行模拟分析,研究了鱼腹式箱梁在自重荷载作用下的真实受力状态,分析了引起鱼腹式箱梁剪滞系数非常规分布的原因,并为此类箱梁的设计、建设提供了经验和参考.结果表明,在自重荷载作用下,鱼腹式箱梁剪滞效应明显;腹板的变形平衡条件不同、剪力分配不均、各腹板中性轴变化速率不等是鱼腹式箱梁剪滞系数非常规分布的主要原因.
鱼腹式箱梁; 有限元; 剪滞系数; 翼板应力; 腹板应力; 腹板挠度; 剪力分配; 中性轴
近些年来,拥有较大抗扭惯性矩、整体性能好以及美观等众多优点的鱼腹形截面箱梁越来越多地进入了群众的视野,特别在城市桥梁和快速路高架桥中得到越来越广泛的应用.曾经备受瞩目的箱梁剪力滞后问题在鱼腹形箱梁的身上再一次引起人们的关注,特别是鱼腹形箱梁的截面端腹板倾斜,横断面的端部受力形式类似悬臂,受力复杂不清晰等问题都对剪力滞后效应产生很大的影响.
剪力滞后这一力学现象在结构工程中比较常见[1].翼板上及不同腹板之间的正应力都是通过剪应力来传递的,在剪力流作用下,翼板产生剪切变形,从而致使腹板附近的正应力与远离腹板位置处正应力产生差异,有时这种差异很大,如果忽略会产生严重安全后果.由圣维南原理[2]可知,荷载的具体形式只影响荷载作用区域附近的应力分布,随着荷载作用区域的远离,这种局部效应影响将变得很小,因而在剪力流的传递过程中,随着腹板的远离,剪力作用产生的剪切变形将呈现非均匀性,正是这种非均匀性造成结构在弯曲时产生的正应力曲线沿横向呈现非均匀分布.这种由于剪力流在传递过程中存在滞后导致结构的正应力在横向呈不均匀分布的现象,称为“剪滞效应”[3-5].在腹板附近考虑剪滞效应时的正应力大于初等梁理论正应力时,称之为“正剪滞效应”,反之称为“负剪滞效应”.剪滞系数公式为λ=考虑剪滞效应时的正应力σ/初等梁理论正应力σ′.正剪滞效应时剪滞系数大于1,负剪滞效应时剪滞系数小于1[6-8].
直腹板箱梁剪滞系数在横向分布与传统计算方法如能量变分法所得结果相近,然而鱼腹式箱梁由于其截面形状和空间受力等原因将与直腹板箱梁呈现不同的剪滞分布.本文通过使用有限元模拟软件对鱼腹形截面箱梁进行了剪滞效应分析,并对其剪滞系数的具体横向分布及引起以上分布问题的原因做进一步分析[9-10].
1 模型建立
本文以沈阳市某高架桥为背景,使用通用有限元软件进行模拟分析.着重探讨自重荷载作用下鱼腹式箱梁剪滞系数分布问题,箱梁截面尺寸如图1所示(单位:m).
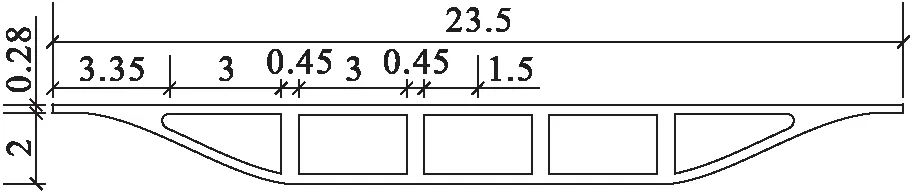
图1 截面尺寸Fig.1 Section dimension
桥梁跨径30 m,桥面宽23.5 m,箱型截面为单箱五室鱼腹形截面,C50混凝土弹性模量E=3.45×1010N/m2,泊松比为0.2,容重为2 450 N/m3,模型两侧端部实心截面部分长1 m.为了便于模型计算,简支边界条件直接作用于端部底板直线段,网格划分采用八节点实体单元,全梁总共划分单元个数为71 164个,有限元网格如图2所示.

图2 有限元网格图Fig.2 Finite element mesh
2 鱼腹式箱梁剪滞效应
2.1 剪滞系数分布
通过对上述模型进行计算,得到全桥模型的应力云图如图3、4所示.由于该桥的宽跨比较大,结构的受力形式更趋近于板,加之边腹板倾斜悬臂的结构形式,使结构受力不清晰,模型经过计算后所得结果可以看出该箱梁应力分布并不均匀,上翼板的受力变形形式与板相似,剪滞效应在图中表现十分明显.

图3 顶板正应力云图Fig.3 Normal stress nephogram of top flange
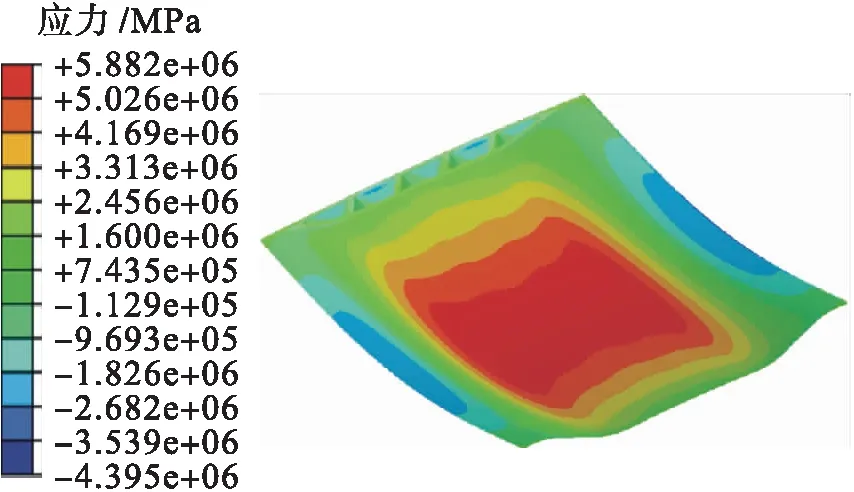
图4 底板正应力云图Fig.4 Normal stress nephogram of bottom flange
使用梁单元建模计算可以得到以平截面假定为基础的初等梁理论的正应力,按照剪滞系数公式进行计算可得到不同位置截面的剪滞系数分布.为了解上下翼板的剪滞系数分布规律,取距端部2、3、5、7.5和15 m截面作为分析截面,并以横截面边缘为参考零点分别取各腹板、翼板中点位参考点对其与初等梁理论计算结果进行对比分析.经计算整理得到该箱梁顶、底板正应力表格及相应的剪滞系数分布曲线,如表1、2和图5所示.
图5中,剪滞系数沿横向分布并不均匀,同一横断面不同位置呈现不同的剪滞效应,例如,距离端部2 m处横截面上出现在2号腹板的剪滞系数已达到1.47,与边腹板的0.9相差较大.边腹板(3号腹板)及其悬臂端翼板一直处于负剪滞效应区,腹板之间区域除部分节段的边腹板与次边腹板(3号和2号腹板)之间部分区域处于负剪滞效应区外,其余大部分腹板间区域处于正剪滞效应区.距离支座较近时,正剪滞系数最大值出现在次边腹板与中腹板间翼板上(1号和2号腹板之间),其最大剪滞系数值为1.47.当所选截面远离支撑端向跨中靠近时,正剪滞系数值逐渐减小且最大值有向横断面中心线靠拢的趋势,距离端部5 m时最大正剪滞系数值已出现在中腹板(1号腹板)上,此时的剪滞系数最大值已减小为1.19.继续向跨中靠近过程中,剪滞系数值仍不断变小,直到跨中位置截面最大剪滞系数减小到其最小值1.08,与此同时,中腹板间翼板上剪滞系数值减小速率明显小于其他部分,且越远离横断面中心线系数的减小速率越大.在上述变化过程的同时,负剪滞效应也不断变小,且变化速率逐渐变慢.随着所选截面远离支撑端部靠近跨中时,剪滞系数值逐渐趋近于1,在0~L/4附近剪滞系数曲线变化较大,其中,L为计算跨径,L/4后变化趋同且相对平缓,越靠近跨中位置,截面应力越趋向近似初等梁理论的平截面假定时的应力,但剪滞效应仍很明显.

表1 横截面顶板应力Tab.1 Stress of top flange on cross section MPa
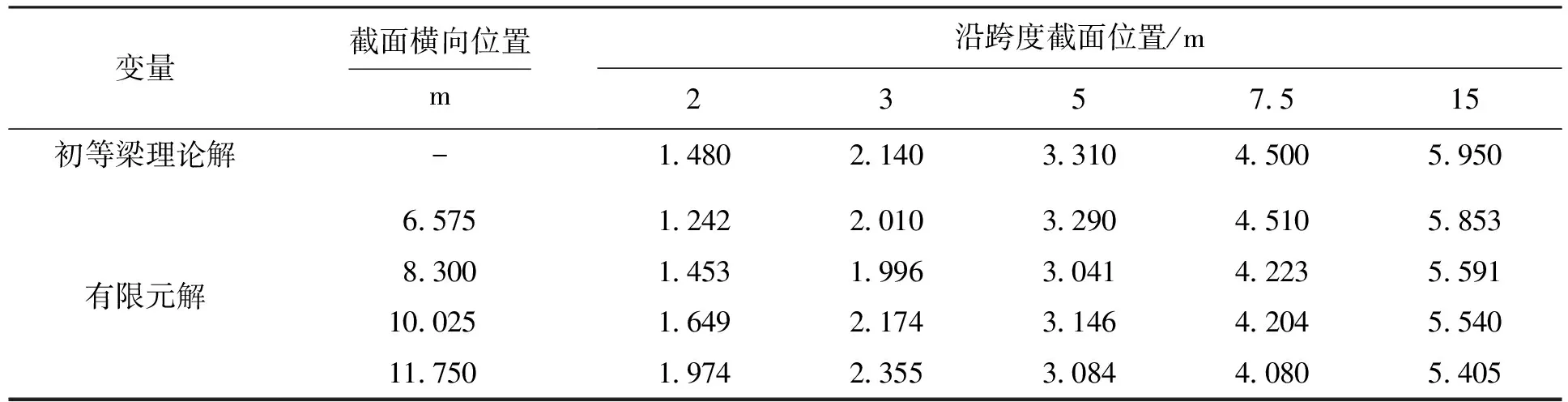
表2 横截面底板应力Tab.2 Stress of bottom flange on cross section MPa
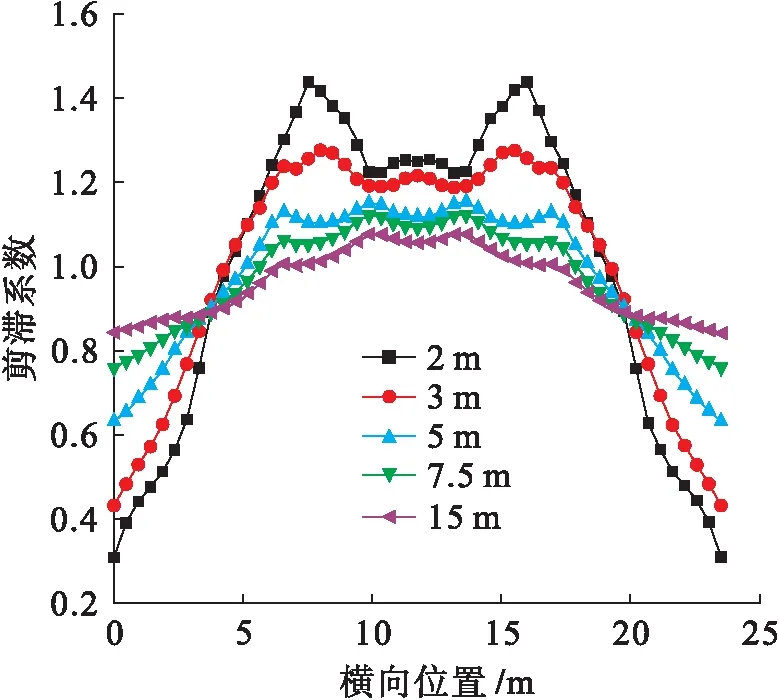
图5 顶板剪滞系数分布Fig.5 Shear lag coefficient of top flange
图6为底板剪滞系数分布.底板同样存在正负剪滞效应分布不均现象,由于边腹板为鱼腹形而且腹板与底板交界不清晰等原因,图6中各曲线两端约0.5 m长度不做讨论.从图6可以看出,底板在距离端部支撑附近时,中腹板(1号腹板)间翼板剪滞系数最大且为正剪滞效应,其最大值为1.35.沿中腹板次边腹板横向变化,正剪滞效应逐渐减小,负剪滞效应逐渐加大.在0~L/4节段曲线变化较大,L/4至跨中节段横截面上剪滞系数曲线变化较缓,同时底板完全由负剪滞效应支配,但剪滞系数值与1接近,因此,此时的计算结果与初等梁理论计算结果相差不是很大.
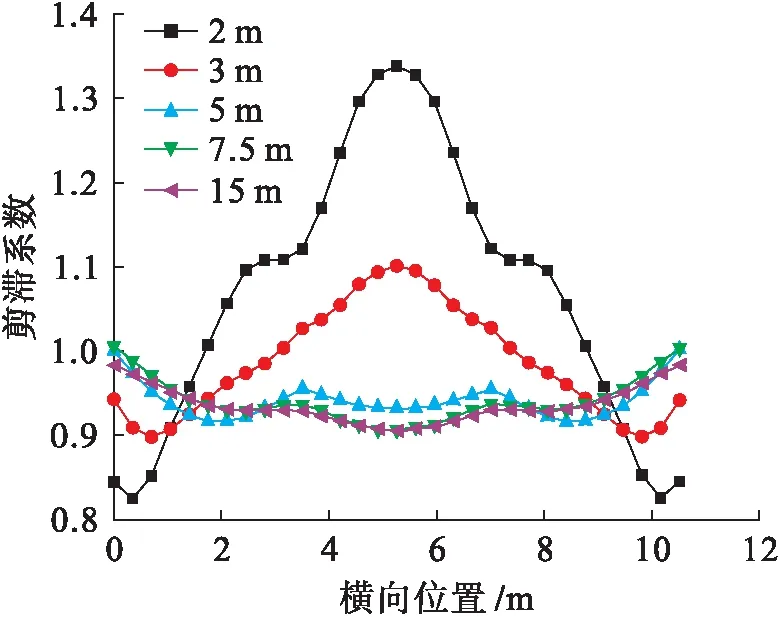
图6 底板剪滞系数分布Fig.6 Shear lag coefficient of bottom flange
由图5、6可知,在0~L/4节段最大剪滞系数出现在翼板中部,而L/4至跨中节段剪滞系数的最大值出现在腹板与翼板交接处.因此,在设计计算过程中应注意0~L/4节段的上、下翼板厚度合理过渡及合理布置钢筋等问题.
2.2 鱼腹式箱梁横向剪滞系数分配
2.2.1 腹板竖向位移及应力
图7为箱梁竖向位移云图.根据圣维南原理,距离端部支撑截面较近处截面应力准确值难以正确计算,本文对端部1 m范围内截面并未加以研究探讨.图8为腹板沿跨度的挠度图,图9为腹板沿跨度的正应力图.由图8、9可知,鱼腹式箱梁整个梁段均存在横向弯曲,横向弯曲挠度从支撑端部截面到跨中截面逐渐加大,跨中截面的横向挠度最大,此时1号与3号腹板在纵向的挠度差值已经达到0.25 mm,而其应力差值已经达到1.4 MPa.鱼腹式箱梁上翼板受力变形与带有加劲肋的板相似,各腹板的作用相当于板上的加劲肋,由于加劲肋的刚度和附加约束作用,板的横向及竖向变形均有一定影响,同时板的附加约束和附加荷载作用也对腹板的变形产生很大的影响,此时鱼腹式箱梁上翼板的变形情况类似板的跨中两外侧边缘加以集中力的作用.由于该箱梁为整体结构,翼板与腹板无清晰分界,它们之间相互制约,腹板对翼板的板效应有削弱作用,翼板由于横向位置不同,相应位置处腹板不同的边界条件(其中包括位移边界条件和应力边界条件)致使各腹板的挠度及应力产生很大区别,由图8、9可以得到不同截面位置处各腹板顶部的位移及正应力的边界条件.
2.2.2 腹板剪力
图10为不同位置截面各腹板的剪力曲线图,可以发现整个箱梁的各个截面一直存在剪力分配不均现象.靠近支撑端部时次边腹板(2号腹板)的剪力值最大,随着所选截面在纵向向跨中靠近时,各截面在横向的最大剪力值不断向中腹板(1号腹板)靠近,当所选截面在跨中(15 m)时,可以看到中腹板承担了大部分剪力.鱼腹形的边腹板(3号腹板)在整个过程中所分配到的剪力相对直腹式的次边腹板和中腹板(2号和1号腹板)要小很多.薄壁结构在对称荷载作用下弯曲时,不同腹板及翼缘板主要通过剪切变形来传递截面的法向正应力,因此,截面上剪力流的分布对该截面的法向应力影响至关重要.图5、6中截面的剪滞系数沿横向分布,并非均匀的三次抛物线、正弦曲线等常见剪滞效应分布形式,其最主要原因是由于鱼腹形截面剪力分布不均导致同一位置横截面的不同横向位置翼板剪切变形不同,且剪切作用使各腹板的中性轴与形心轴发生偏移,各腹板的剪力流分布不同致使各腹板中性轴发生不同程度的偏移,使各腹板的应力产生较大差异,上述原因引起箱梁截面的纵向正应力分布曲线呈现出非均匀的高次抛物线形式.
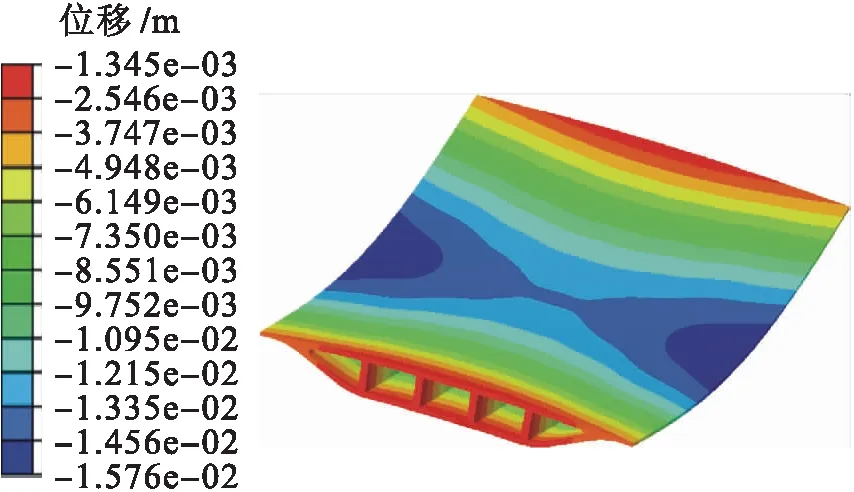
图7 箱梁竖向位移云图Fig.7 Vertical displacement nephogram of box beam

图8 腹板沿跨度挠度图Fig.8 Deflection of different webs along span
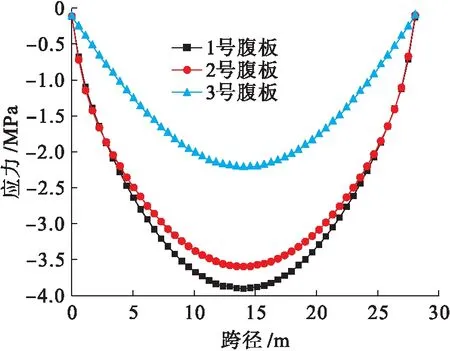
图9 腹板沿跨度正应力图Fig.9 Normal stress of different webs along span
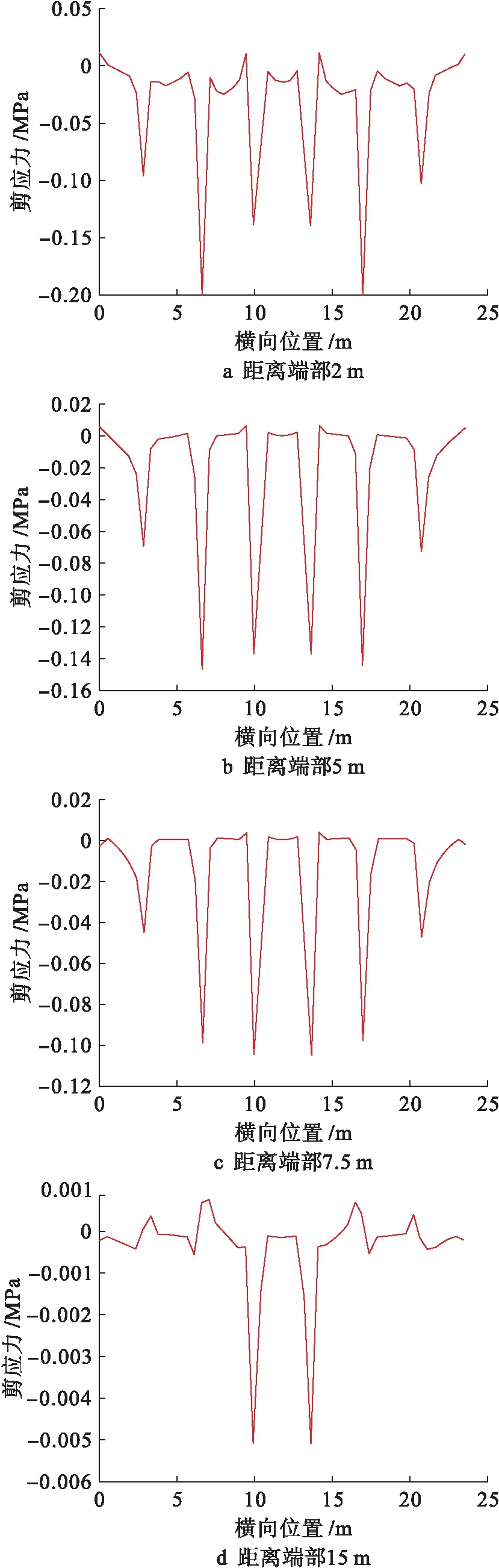
图10 腹板与顶板交接处剪应力Fig.10 Shear stress at junction betweenweb and top flange
2.2.3 中性轴位置
沿箱梁跨度方向位置截面对腹板截面上的应力进行插值计算,可得到各腹板应力零点位置(即中性轴位置),边腹板由于其特殊性暂不讨论,只对1号腹板、2号腹板进行对比分析.各腹板中应力零点位置如图11所示.

图11 腹板应力零点图Fig.11 Stress zero point curves of webs
由图11可以看出,1号和2号腹板在端部位置截面和跨中截面的应力零点(中性轴)在竖向并未在同一高度.通过将1(2)和1(15)差值与2(2)和2(15)差值进一步对比分析可以看出,1号腹板的中性轴变化率较2号腹板大.上述分析说明初等梁理论中平截面假定理论不再适用于此类箱梁的设计计算.
3 结 论
此类箱梁截面边腹板部分的受力形式类似悬臂结构,对主梁的横向弯曲影响很大,加之边腹板倾斜,使剪力的分配及传递变得复杂,由于此类箱梁截面宽度较宽,截面受力变形趋近于板.综上在对此类箱梁特别是宽跨比较大的梁桥做设计计算时,已不再适合继续使用平截面假定为基础的初等梁理论计算,而应对其进行实体分析计算,应对剪滞效应多加重视.引起横向弯曲的面内横向应力及变形、端部至L/4附近截面抗剪强度验算等问题亦多加考虑不应忽略.
[1] 王继兵,周德源,秦荣.箱梁剪滞效应分析样条有限点法 [J].沈阳工业大学学报,2010,32(5):596-600.
(WANG Ji-bing,ZHOU De-yuan,QIN Rong.Spline finite point method for shear lag analysis of box girder [J].Journal of Shenyang University of Technology,2010,32(5):596-600.)
[2] Timoshenko S P,Goodier J N.弹性理论 [M].北京:高等教育出版社,2013.
(Timoshenko S P,Goodier J N.Theory of elasticity [M].Beijing:Higher Education Press,2013.)
[3] Zhang Y H.Improved finite-segment method for analyzing shear lag effect in thin-walled box girders [J].Journal of Structural Engineering,2012,138(10):1279-1284.
[4] 蔺鹏臻,刘凤奎,杨军,等.箱梁剪滞翘曲位移函数的定义及其应用 [J].计算力学学报,2012,29(5):789-794.
(LIN Peng-zhen,LIU Feng-kui,YANG Jun,et al.Definition and application of shear-lag warping displacement functions for box girders [J].Chinese Journal of Computational Mechanics,2012,29(5):789-794.)
[5] 周世军.箱梁的剪力滞效应分析 [J].工程力学,2008,25(2):204-208.
(ZHOU Shi-jun.Shear lag analysis of box girders [J].Engineering Mechanics,2008,25(2):204-208.)
[6] 雒敏,蔺鹏臻,孙理想.单箱双室箱梁的剪力滞效应分析 [J].力学与实践,2013,35(6):70-74.
(LUO Min,LIN Peng-zhen,SUN Li-xiang.Analysis of shear lag effect of twin-cell box girders [J].Mechanics in Engineering,2013,35(6):70-74.)
[7] 张元海.箱形梁桥剪力滞效应及温度效应理论研究及其应用 [D].成都:西南交通大学,2008.
(ZHANG Yuan-hai.Theory study and application of shear-lag and temperature effect in box-girder bridges [D].Chengdu:Southwest Jiaotong University,2008.)
[8] 郭金琼,房贞政,郑振.箱形梁设计理论 [M].北京:人民交通出版社,2008.
(GUO Jin-qiong,FANG Zhen-zheng,ZHENG Zhen.Design theory of box girder [M].Beijing:China Communications Press,2008.)
[9] Song Q,Scordelis A C.Formulas for shear-lag effect of T-,I-,and box beams [J].Journal of Structural Engineering,1990,116(5):1306-1318.
[10]Luo Q Z,Li Q S,Tang J.Shear lag in box girder bridges [J].Journal of Bridge Engineering,2002,7(5):308-313.
Shearlageffectanalysisformulti-cellfish-belliedboxbeam
ZHANG Hai, JIN Yu-jia
(School of Traffic Engineering, Shenyang Jianzhu University, Shenyang 110168, China)
In order to solve the problem that the distribution states of stress and shear lag effect of multi-cell fish-bellied box beam are different with those of traditional box beam, the simulation analysis was carried out with finite element software, and the real stress states under the self-weight load effect of fish-bellied box beam were investigated. In addition, the reasons for the un-normal distribution of shear lag coefficient of fish-bellied box beam were analyzed, which could provide the experience and references for the design and construction of the box beams. The results show that under the self-weight load effect, the shear lag effect of fish-bellied box beam is obvious, and the main reasons for the un-normal distribute of shear lag coefficient of fish-bellied box beam are the different deformation balance conditions of webs, different shear distribution and unequal change rate of neutral axis of various webs.
fish-bellied box beam; finite element; shear lag coefficient; flange stress; web stress; web deflection; shear distribution; neutral axis
2016-08-31.
住房和城乡建设部软科学研究计划项目(K42016146).
张 海(1972-),男,辽宁沈阳人,副教授,博士,主要从事桥梁美学和桥梁振动等方面的研究.
* 本文已于2017-01-19 17∶56在中国知网优先数字出版. 网络出版地址: http:∥www.cnki.net/kcms/detail/21.1189.T.20170119.1756.018.html
10.7688/j.issn.1000-1646.2017.06.20
TU 997
A
1000-1646(2017)06-0710-06
(责任编辑:钟 媛 英文审校:尹淑英)
