基于能量最小多尺度曳力模型的搅拌槽内气液两相流计算液体力学模拟及实验研究

李新菊，管小平，杨宁，刘明言

（1天津大学化工学院，天津 300350；2中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190）

基于能量最小多尺度曳力模型的搅拌槽内气液两相流计算液体力学模拟及实验研究

李新菊1，2，管小平2，杨宁2，刘明言1

（1天津大学化工学院，天津 300350；2中国科学院过程工程研究所多相复杂系统国家重点实验室，北京 100190）

采用双电导探针和欧拉-欧拉双流体模型对涡轮桨搅拌槽内局部气液分散特性分别进行了实验和三维计算流体力学（CFD）数值模拟研究。重点研究了转速对搅拌槽上下循环区局部气含率分布、全槽液相流场和湍动动能的影响。实验表明，转速对上循环区气含率分布的影响大于下循环区，且上循环区气含率随转速的增大而增大。CFD模拟比较了TOMIYAMA曳力模型和基于能量最小多尺度理论（EMMS）的DBS-Local曳力模型对局部气含率的预测结果。结果显示DBS-Local曳力模型能够较好地预测出不同搅拌转速下搅拌槽循环区气含率径向分布；TOMIYAMA曳力模型只能定量预测出低搅拌转速下（140r/min，280r/min）循环区的气含率分布，高转速下（420r/min，560r/min）该曳力模型不能模拟出下循环区壁面附近的气体，且低估了上循环区气含率。

搅拌槽；气液两相流；电导探针；能量最小多尺度；计算流体力学

气-液搅拌槽因具有传热传质效率高、相间接触面积大、操作简单等优点被广泛地应用于石油、化工、水处理等行业。气体分散特性是搅拌槽内重要的流体力学行为，反映了局部相含率、混合及传热传质特性，为搅拌槽的设计和放大提供重要信息。不少学者尝试采用实验手段检测气液搅拌槽内气体的分散特性[1-5]。李良超等[6]采用电导探针法研究了双层桨搅拌槽内气体的分散特性，发现在叶轮区气含率沿径向减小，在循环区域气含率沿径向先增加后减小。KONG等[7]采用γ-CT法对不同流型下排出流区的气含率进行了测量，发现气含率在搅拌桨附近存在一个峰值，且气体分布器上孔的数量和直径对气含率的影响可以忽略。RAMMOHAN[8]采用137Cs γ-ray CT法对标准涡轮桨搅拌槽进行实验研究。较高转速下搅拌桨的转动引起的转轴振动使得最大转速不能超过400r/min，相应的最大通气量只能设为7.5L/min。

受实验检测技术的限制，现有气-液搅拌槽的实验测量手段难以给出精细的时空多尺度流场信息；而计算流体力学（CFD）能获得流场的精细结构，是搅拌槽设计和放大的重要潜在方法。近年来，随着计算机技术的发展，越来越多的学者采用CFD的方法模拟搅拌槽内气液两相分散特性[9-12]。KHOPKAR和TANGUY[13]采用多重参考系方法（multiple-reference-frame，MRF）对双层桨气液搅拌槽进行研究，得到了不同操作条件下搅拌槽内的流型、气含率分布等，结果显示CFD模拟能够捕捉到不同流型下流体的流动特性。RANADE和AKKER[14]对搅拌槽内气液两相流动进行模拟研究。结果发现，模拟的轴向和切向速度以及气含率分布均和实验值变化趋势一致，但对湍动动能的预测结果和实验值偏差较大。

气液相间作用力是引起气液搅拌槽与单相搅拌槽流体力学行为不一致的重要原因之一，建立可靠的相间作用力模型是准确预测气体分散性的关键。SCARGIALI等[15]指出，在气液搅拌槽中虚拟质量力、升力、湍流耗散力远远小于曳力，模拟中可以仅考虑曳力的作用。陈雷和高正明[16]采用Grace曳力模型对多层桨气液搅拌槽进行研究。结果发现，CFD耦合群平衡（PBM）的方法能准确预测出气含率的双峰分布，但是在定量上仍存在明显不足，尤其是在顶层桨上方及中层桨的排出流区。李良超等[17]采用SCHILLER-NAUMANN[18]曳力模型研究了双层桨搅拌槽内的气含率分布，结果表明该模拟可以得到气含率的双峰分布趋势，但在槽底和出口附近模拟值较实验值偏小。杨宁等[19-22]在研究鼓泡塔内气液流动时，通过考虑气液的非均匀结构和能量多尺度耗散提出了一种基于能量最小多尺度理论（energy-minimization multi-scale，EMMS）的双气泡尺寸模型（dual-bubble-size，DBS），该模型中采用稳定性条件来封闭气泡的力平衡方程，得到气液稳约多流体模型（stability-constrained multi-fluid model，SCMF）。参考SCMF模型，肖颀[23]分析鼓泡塔内相间作用力和结构参数之间的关系，建立了CD/db和表观气速之间的关系（DBS-Global曳力），研究表明该模型能提高对鼓泡塔和气液搅拌槽内气含率的预测精度[23-24]。蒋雪冬[25]认为在湍流状态下反应器内流体流动具有不均匀性，相间曳力与局部流动参数有关，此时DBS-Global曳力模型可能无法体现反应器内流体流动的非均匀性，在DBS-Global模型的基础上进行改进，将CD/db表示为流体局部结构参数的形式，并与CFD耦合得到了DBS-Local曳力模型。目前DBS-Local曳力模型已经在外环流提升管反应器和内环流气升式反应器的模拟中得到应用[25-27]。

本文作者采用双电导探针法对固定通气量下搅拌槽内循环区域局部气含率随转速的变化趋势进行了研究。同时采用CFD数值模拟的方法研究了不同转速下气含率分布、液相宏观流场以及湍动动能分布，文中采用TOMIYAMA曳力模型[28]和DBS-Local曳力模型[25]计算相间曳力，对比了两种曳力对搅拌槽循环流区气含率的预测精度，验证了DBS-Local曳力模型在气液搅拌槽模拟中的适用性。

1 搅拌槽装置及测试方法

本文研究的搅拌槽是直径为T=200mm的平底有机玻璃槽，如图1所示。槽内均匀分布4块挡板，挡板宽T/10。液位高度H=T，搅拌桨采用六直叶涡轮桨，搅拌桨直径D=T/3，距离槽底C=90mm，搅拌桨叶片宽w=D/4，高l=D/5。搅拌桨和槽底之间安装直径为T/3的不锈钢环形气体分布器，分布器距槽底25mm，分布器上均匀分布8个直径为1.5mm的小孔用来通气。采用自来水作为连续相，空气作为分散相，实验过程中固定空气流量Qg=1.59vvm[vvm为单位体积液体在单位时间内通入压缩空气量，单位为m3/(m3·min)，下同]。实验采用双电导探针测量不同高度（z=1/3H和z=2/3H）、不同转速（N=140r/min，280r/min，420r/min，560r/min）下循环区域的气含率分布。电导探针根据气液两相电导率不同的原理来进行测量。实验中每个截面选取5个测量点，每个测量点测五组数据，每组数据采样时间为20s，最后将5组数据取平均得到该测量点的局部气含率，电导探针采样频率20kHz。

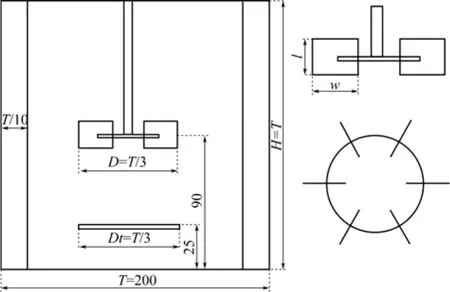
图1 搅拌槽结构与尺寸（mm）

2 CFD模拟

2.1 基本控制方程

对搅拌槽内气液两相数值模拟中采用欧拉-欧拉两相流方法，气液两相的流体控制方程如式(1)、式(1)。

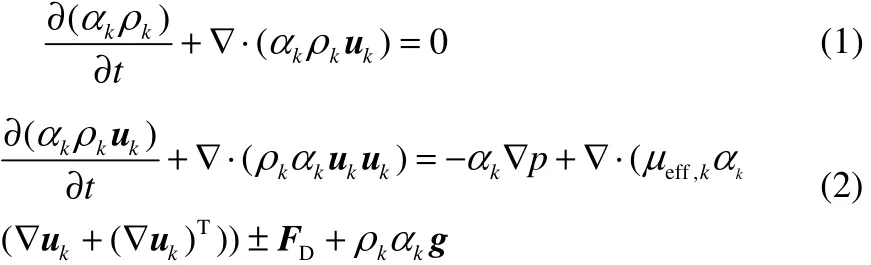
式中，ρk、αk和uk分别代表密度、体积分数和相平均速度，下角标k代表气相（k=g)或液相(k=l)；FD为相间动量交换项；μeff,k为k相的有效黏度；p为压力。FD和μeff,k需要由合适的封闭模型给出。

在本研究中只考虑了曳力的作用。气泡群的曳力可通过式(3)关联式计算得到。

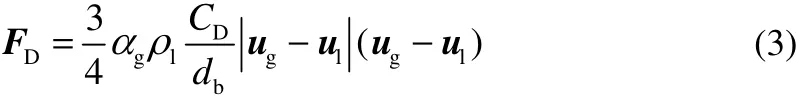
式中，CD为曳力系数，本文中采用TOMIYAMA曳力模型[28]和DBS-Local曳力模型[25]来计算相间曳力，TOMIYAMA曳力模型方程可表示为式(4)。

式中，CD0为静止的无限大流场中单气泡所受到的曳力大小，气泡群曳力系数往往通过修正得到，本文采用的修正形式如式(5)。

式中，p为修正因子，本研究中取1，模拟中假设气泡大小均一，大小取4mm。

和TOMIYAMA曳力模型不同，DBS-Local曳力模型将曳力系数和气泡直径的比值（CD/db）看作一个整体结构参数，由当地局部气速和液速计算得到，计算中不需要指定特定的db值。

DBS-Local曳力模型如式(6)。

式中，每个网格内的表观气速和液速需要根据式(7)、式(8)进行计算。

本研究采用标准k-εmixture湍流模型来封闭质量和动量守恒方程，如式(9)、式(10)。

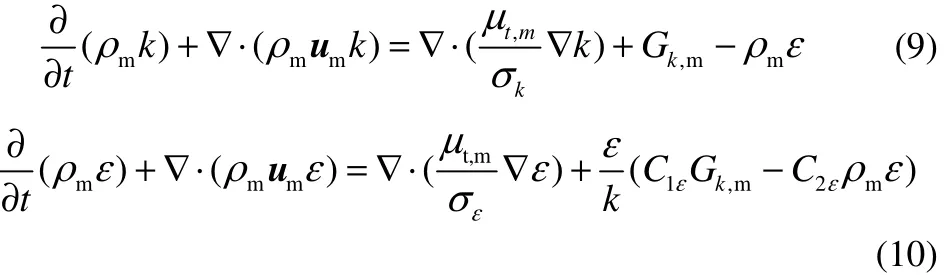
式中，Gk,m为湍动能产生项，kg/(m·s3)；k为湍动能，m2/s2；ε为湍流耗散率，m2/s3；μt,m为混合相湍流黏度，kg/(m·s)；ρm为混合相密度，kg/m3；um为混合相速度，m/s。动能产生项Gk,m计算公式如式(11)。

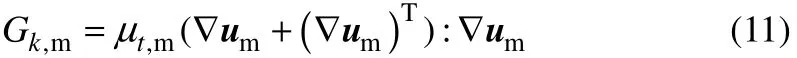
方程中所涉及到的参数值为：C1ε=1.44、C2ε=1.92、Cμ=0.09、σk=1.0、σε=1

2.2 模拟设置

本研究采用Fluent前处理软件Gambit 2.4.6进行构体网格划分，网格量为314094，根据文献比较分析可知该网格量已经足够精细[12,29]。如图2所示，搅拌桨区域及分布器区域为非结构化网格，其余区域为结构化网格。本文使用Ansys Fluent 15.0进行模拟计算，搅拌槽槽体、挡板、搅拌桨及转轴均设为无滑移壁面条件；搅拌槽顶部自由液面采用degassing边界条件，即允许离散相从顶部逸出，不允许连续相通过。模拟中采用稳态的MRF法处理旋转的桨叶，故需将计算域划分为内外两个区域，通过界面（interface）进行数据传递。搅拌桨绕旋转轴转动，带动周围液体（常温常压的水）流动，空气由环形分布器通入搅拌槽内。采用SIMPLE算法求解速度-压力方程，一阶迎风格式离散动量方程和湍流方程。

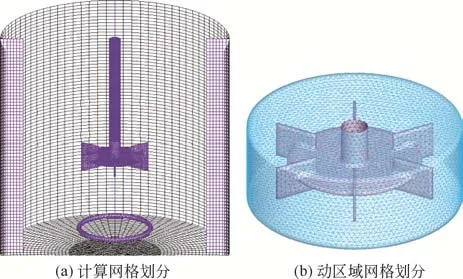
图2 计算区域和网格划分

3 结果与讨论

3.1 气含率的实验结果

在通气量Qg为1.59vvm时，不同转速下搅拌槽下循环区（z= 1/3H）及上循环流区（z=2/3H）气含率的径向分布曲线如图3所示。从图中可以看出，不同操作条件下搅拌槽内的局部气含率不同，同一操作条件不同位置的气含率也存在较大差别。在下循环区域[图3(a)]，不同转速下气含率的变化趋势相同，最大值出现在量纲为1半径为0.3处，即气体分布器附近。转速为140r/min和280r/min时，气含率在量纲为1半径大于0.6的边壁附近基本为0，转速继续增加该区域的气含率随之增大。这是由于转速越大，搅拌桨的泵出能力增大，液相循环量增大；此外，相比于浮力，液相对气体的夹带作用占主导作用，随之被夹带到搅拌桨下方区域的气体量增加，气含率随半径的增大呈现出先增大后减小再增大的趋势。

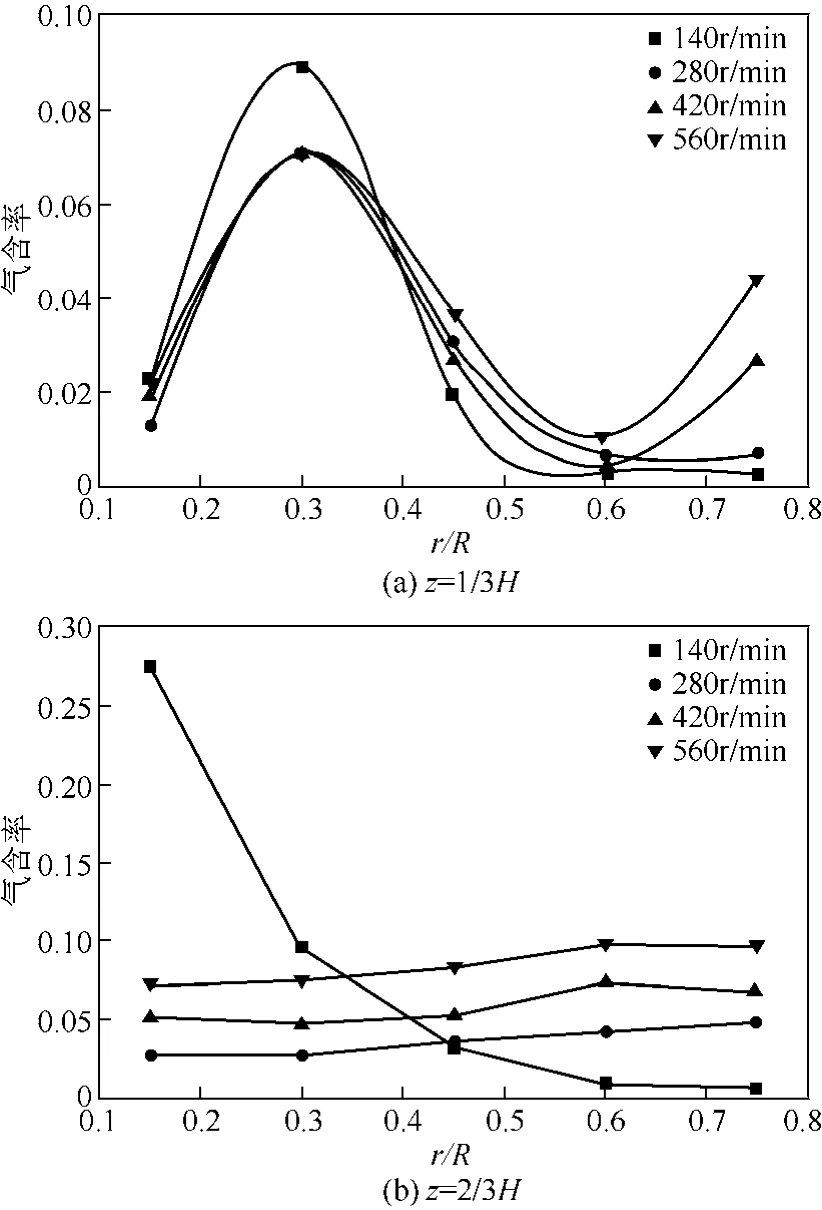
图3 不同高度处气含率随转速的径向变化曲线

上循环流区[图3(b)]气含率随转速的变化情况比较复杂，极低的转速下（140 r/min），气体主要集中在转轴附近，随径向距离的增大气含率急剧减小。这主要是因为在极低的转速下搅拌桨的分散作用微弱，气体能够穿过旋转的桨叶上升，此时搅拌槽类似于中心进气的鼓泡塔；当转速增大到280 r/min以后气体逐渐开始分散开并充满整个搅拌槽上方区域，气含率随转速的增大而增加。这是因为在气体流量Qg为1.59vvm时，转速达到280 r/min就可以将气体分散到搅拌槽的上循环区。进一步增大搅拌转速，被液相所夹带的气体量越大，循环区各点的气含率都随之增大。

3.2 CFD模拟

3.2.1 气含率分布

图4和图5给出了通气量Qg为1.59vvm时，转速分别为N=140r/min、280r/min、420r/min和560r/min操作工况下不同高度处（z=1/3H，z=2/3H）CFD预测的气含率径向分布与实验对比曲线。

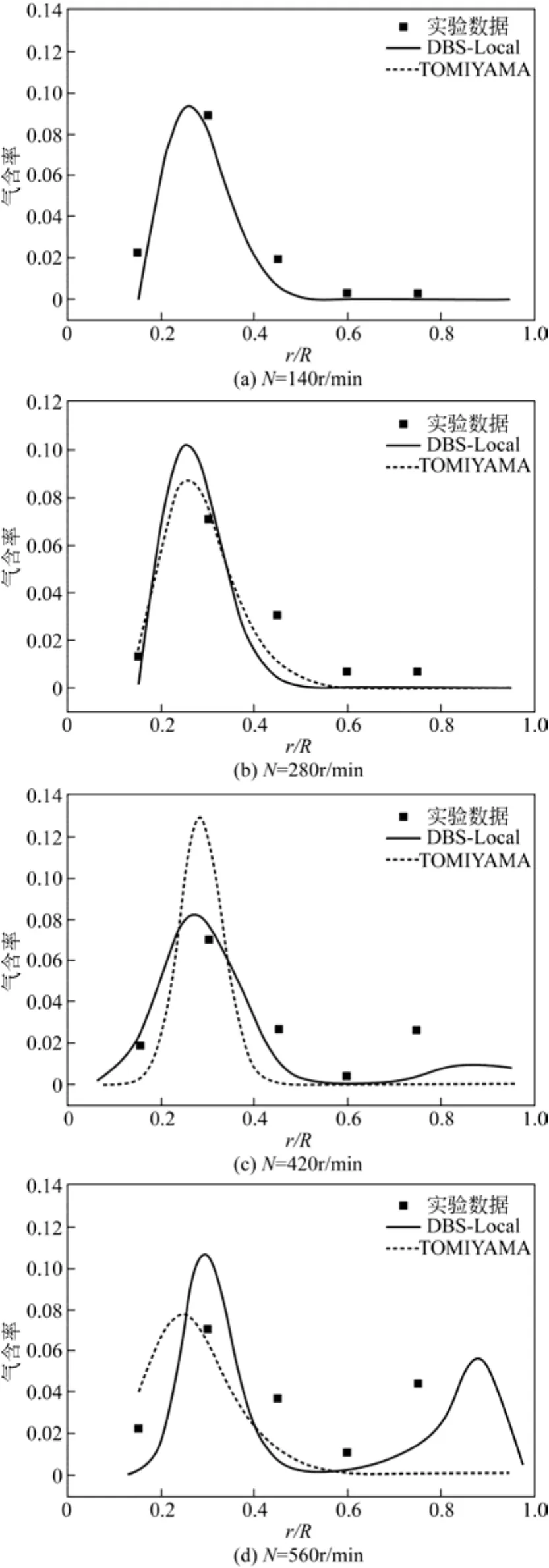
图4 不同转速下CFD预测的气含率径向分布

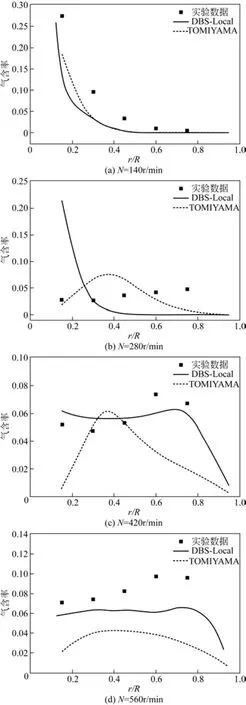
图5 不同转速下CFD预测的气含率径向分布

从图4可以看出，低转速下（140r/min、280r/min），两种曳力模型对气含率径向分布的预测均能和实验值吻合较好。增大搅拌转速（420 r/min，560r/min），DBS-Local曳力模型仍能定性预测出下循环区壁面附近局部气含率随转速的增加而增大的这一变化趋势，但在定量上对气含率的预测和实验测量值还存在一定差距。转速N=420r/min下，实验中可以明显观察到部分气体被循环液相带到搅拌桨下方。采用DBS-Local曳力模型模拟的壁面附近气含率略小于实验值，气体在搅拌桨的作用下逐渐在搅拌桨上方分散，只有很少一部分气泡被液相夹带到桨叶下方壁面附近区域；转速增大到560r/min后，被夹带到下循环区的气量增大，壁面附近气含率出现局部极大值点，这和实验测量结果相吻合。而高转速下TOMIYAMA曳力模型预测的下循环区壁面附近气含率几乎为零，这与实验中观察到的现象不符。

从图5可以看出，DBS-Local曳力模型和TOMIYAMA曳力模型均能描述随转速增大气体由转轴附近向整个槽体扩散的趋势，但定量上对上循环区气含率的预测还和实验值之间存在一定差距。当转速从140r/min增大到280r/min的过程中，DBS-Local曳力模型可以定性预测出气含率分布变化的转折现象，即气体开始在搅拌桨上方区域沿径向分散，在高转速下气含率在靠近壁面处升高；而TOMIYAMA模型与实验相差较大。在转速N=280r/min操作条件下实验中可以观测到气体不再沿着转轴上升，而是已经开始在搅拌桨上方区域分散，采用DBS-Local曳力模型的计算结果和低转速（140r/min）几乎相同，气体仍然在转轴附近富集；而TOMIYAMA曳力模型能够模拟出转速N=280r/min下气体在搅拌桨上方分散开这一现象。高转速下（420r/min，560r/min）DBS-Local曳力模型预测的上循环区气含率径向分布和实验值吻合较好，TOMIYAMA曳力模型预测的气含率远远低于实验测量值。

需要指出的是，DBS-Local曳力模型的模拟结果与实验仍有一定的差异。该模型是基于鼓泡塔内气液两相流建立的，而搅拌桨的存在导致搅拌槽内的流体流动、能量输入和耗散机制不同于鼓泡塔，下一步工作仍需对DBS-Local曳力模型进行修正，使之能更好地用于搅拌槽模拟中。考虑到一般工业混合过程中为了达到更好的混合效果，搅拌转速比较高，本文以下部分主要讨论了采用DBS-Local曳力模型对气液搅拌槽内局部气液分散特性的模拟结果。

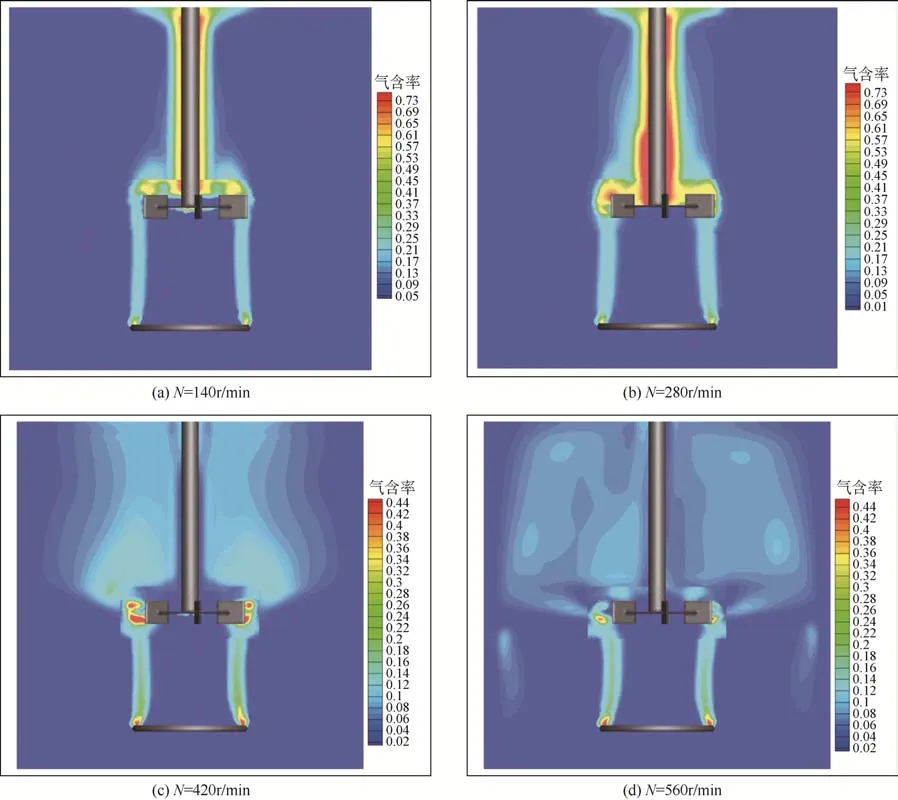
图6 垂直截面气含率分布

图6给出了采用DBS-Local曳力模型计算不同操作条件下相邻两挡板间垂直截面的气含率分布云图。在气液搅拌槽中，气体的分散特性是由上升的气流和搅拌桨的分散作用两种不同的控制机制共同决定的。从图6中可以看出，低转速下搅拌桨对气体的分散作用极其微弱，气体主要集中在搅拌桨和转轴附近，转轴附近气含率很高，其他区域气含率几乎为零，气体在搅拌槽内的分散性很差；随着转速的增大，搅拌桨的分散作用增强，气体逐渐被桨叶分散并充满搅拌桨上方区域，由于浮力的作用，很少有气体被夹带到下循环区；进一步增大转速，搅拌桨的分散作用占据主导地位，液相的循环量增大，一部分气体被循环液体带到下循环区，在整个搅拌槽内都可以观测到气体的存在，且搅拌桨以上区域的气体分布比较均匀。

3.2.2 宏观流场

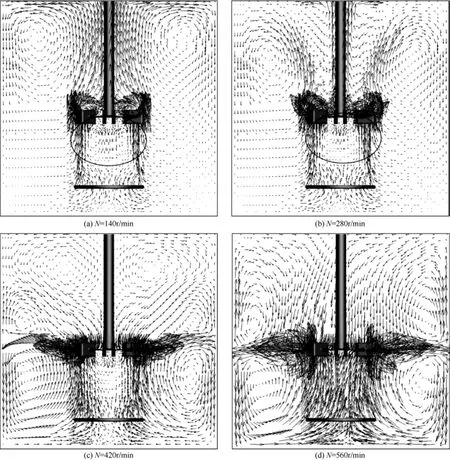
图7 液相宏观流场

图7给出了采用DBS-Local曳力模型计算的不同转速下液相宏观流场。气液搅拌槽内流体的流动受气体上升作用和搅拌桨分散作用两种机制协调控制[24]。从图7(a)中可以看出搅拌桨转速较低时，气体的运动主要是由下向上的运动，在上升气体的作用下，液相由搅拌槽的中心向上运动，到达液面附近后沿槽壁向下形成一个较大的液相回流；同时在桨叶下方分布器所在的圆柱形区域内形成一个小的循环涡，如图7(a)中圆圈内所示）。随着转速增大到280r/min，大的液相涡向下移动同时向转轴中心靠拢；桨叶下方的小循环涡在减小的同时也逐渐向转轴中心靠拢，如图7(b)。继续增大搅拌桨转速到420r/min，搅拌桨的作用明显增强，液相由搅拌桨排出后形成两个循环涡，这两个循环涡在上升气体的作用下向上倾斜；同时，上升气体引起的液相环流继续向转轴中心靠近，并被压缩到槽体上部区域，桨叶下方的小涡消失，此时搅拌槽内三个液相循环涡并存，如图7(c)。搅拌桨转速进一步增大到560r/min，如图7(d)，搅拌桨的作用开始占主导，上升气体引起的液相涡消失；高速旋转的搅拌桨在桨叶排出流区产生径向水平射流，在射流的作用下周围的液相撞击到槽壁后分别向上和向下流动。向上流动的液相在上升过程中逐渐向轴中心靠拢；向下流动的液体到达槽底后沿槽底向中心靠拢，从而在搅拌桨的上下位置分别形成两个涡，这同王卫京[30]得到的结果一致。

3.2.3 湍动动能

图8给出了采用DBS-Local曳力模型计算得到的不同操作工况下相邻两挡板间垂直截面的湍动动能分布云图。从图中可以看出湍动动能随转速的变化趋势和液相宏观流场类似。在极低的转速下由于上升气体的作用使得转轴附近的湍动增强；提高转速（280r/min），搅拌桨作用逐渐增强上升气体的作用范围逐渐增大，搅拌桨上方的湍动动能增大；进一步增大搅拌速度，搅拌桨分散作用加强，排出流区湍动增强，但此时上升气体的作用仍然比较明显，使得最大湍动动能出现在搅拌桨中心偏上的位置，也就是液相的射流区域；继续增大转速，搅拌桨的分散作用完全占据主导地位，湍动动能的最大值出现在搅拌桨的水平射流平面内，且最大值远远大于其他转速下的湍动动能。

4 结论

图8 垂直截面湍动动能分布云图

DBS模型是能量最小多尺度（EMMS）理论在气液两相流中的扩展。本文对气液搅拌槽内的局部气液分散特性进行了实验和三维稳态CFD模拟，首次将DBS-Local曳力模型用于搅拌槽的气液两相流CFD模拟，比较了DBS曳力模型和TOMIYAMA曳力模型对循环区气含率径向分布的预测结果，主要结论如下。

（1）实验研究发现，搅拌槽的上循环区气含率随转速的增大而增大；转速对搅拌桨下循环区域气含率的影响小于上循环区。转速越大，被夹带到搅拌桨下方的气体越多。

（2）对于搅拌桨下方区域，DBS-Local曳力模型能较好地模拟出不同转速下气含率的径向分布，但难以预测TOMIYAMA曳力模型只能较好地预测出低转速下（140r/min，280r/min）的气含率径向分布；但高转速下（420r/min，560r/min）搅拌桨下方气体沿径向向壁面的扩散规律。

（3）DBS-Local曳力模型能定性预测出搅拌槽上循环区气含率随转速的变化趋势。对于上循环区的气含率模拟，DBS-Local曳力模型相比于传统的TOMIYAMA曳力模型具有明显的优势：DBS-Local曳力模型预测的气含率和实验值相差较小，而TOMIYAMA曳力模型远远低估了高转速时上循环区的气含率。

（4）DBS-Local曳力模型能在一定程度上提高对搅拌槽内气含率的预测精度，可为气液搅拌槽的CFD模拟提供一种新的曳力模型。

符号说明

C—— 搅拌桨距槽底高度，mm

CD—— 曳力系数

D—— 搅拌桨直径，m

db—— 气泡直径，m

FD—— 相间曳力，kg/(m2·s2)

g—— 重力加速度，9.81kg·m/s2

H—— 搅拌槽中液位高度，m

l—— 搅拌桨高度，mm

N—— 转速，r/min

Qg—— 通气量，m3/(m3·min)

T—— 搅拌槽直径，m

Ug’—— 局部气速，m/s

w—— 搅拌桨宽度，mm

α—— 体积分数

μeff—— 有效黏度，Pa·s

ρ—— 密度，kg/m3

下角标

g —— 气相

l——液相

[1] LAAKKONEN M，HONKANEN M，SAARENRINNE P，et al. Local bubble size distributions，gas-liquid interfacial areas and gas holdups in a stirred vessel with particle image velocimetry[J]. Chemical Engineering Journal，2005，109（1）：37-47.

[2] BAO Y Y，CHEN L，GAO Z M，et al. Local void fraction and bubble size distributions in cold-gassed and hot-sparged stirred reactors[J].Chemical Engineering Science，2010，65（2）：976-984.

[3] VESSELINOV H H，STEPHAN B，UWE H，et al. A study on the two-phase flow in a stirred tank reactor agitated by a gas-inducing turbine[J]. Chemical Engineering Research and Design，2008，86（1）：75-81.

[4] 高娜，包雨云，高正明. 多层桨搅拌槽内气-液两相局部气含率研究[J]. 高校化学工程学报，2011，25（1）:11-17.GAO N，BAO Y Y，GAO Z M. Local void fraction in a sparged reactor with a multi-impeller agitator[J]. Journal of Chemical Engineering of Chinese Universities， 2011，25（1）：11-17.

[5] RANADE V V，PERRARD M，XUEREB C，et al. Influence of gas flow rate on the structure of trailing vortices of a rushton turbine: PIV measurements and CFD simulations[J]. Chemical Engineering Research and Design，2001，79（A8）：957-964.

[6] 李良超，王嘉骏，顾雪萍，等.双层桨搅拌槽内局部气液分散特性研究[J]. 浙江大学学报（工学版），2009，43（3）：463-467.LI L C，WANG J J，GU X P，et al. Study on local gas-liquid distribution in dual-impeller aerated stirred vessel[J]. Journal of Zhejiang University（Engineering Science），2009，43（3）：463-467.

[7] KONG L N，LI W，HAN L C，et al. On the measurement of gas holdup distribution near the region of impeller in a gas–liquid stirred Rushton tank by means of γ-CT[J]. Chemical Engineering Journal，2012，188：191-198.

[8] RAMMOHAN A R. Characterization of single and multiphase flows in stirred tank reactors[D]. St Louis：Washington University，2002.

[9] PETITTI M，VANNI M，MARCHISIO D L，et al. Simulation of coalescence，break-up and mass transfer in a gas-liquid stirred tank with CQMOM[J].Chemical Engineering Journal，2013，228：1182-1194.

[10] ZHANG Q H，YANG C，MAO Z S，et al. Large eddy simulation of turbulent flow and mixing time in a gas-liquid stirred tank[J].Industrial and Engineering Chemistry Research，2012，51（30）：10124-10131.

[11] HAN L C，LIU Y J，LUO H A. Numerical simulation of gas holdup distribution in a standard Rushton stirred tank using discrete particle method[J]. Chinese Journal of Chemical Engineering，2007，15（6）：808-813.

[12] ZHANG Y H，BAI Y L，WANG H L. CFD analysis of inter-phase forces in a bubble stirred vessel[J]. Chemical Engineering Research and Design，2013，91（1）：29-35.

[13] KHOPKAR A R，TANGUY P A. CFD simulation of gas-liquid flows in stirred vessel equipped with dual rushton turbines: influence of parallel，merging and diverging flow configurations[J]. Chemical Engineering Science，2005，63（14）：2215-2229.

[14] RANADE V V，AKKER H E A V D. A computational snapshot of gas-liquid flow in baffled stirred reactors[J]. Chemical Engineering Science，1994，49（24b）： 5175-5192.

[15] SCARGIALI F，D’ORAZIO A，GRISAFI A，et al. Modelling and simulation of gas–liquid hydrodynamics in mechanically stirred tanks[J]. Chemical Engineering Research and Design，2007，85（5）：637-646.

[16] 陈雷，高正明. 多层桨气-液搅拌反应器内局部特性的数值模拟[J].北京化工大学学报（自然科学版），2010，37（3）：14-19.CHEN L，GAO Z M. Numerical simulation of local characteristics in an aerated stirred tank with multiple impellers[J]. Journal of Beijing University of Chemical Technology（Natural Science），2010，37（3）：14-19.

[17] 李良超，王嘉骏，顾雪萍，等.气液搅拌槽内气泡尺寸与局部气含率的CFD模拟[J].浙江大学学报（工学版），2010，44（12）：2396-2415.LI L C，WANG J J，GU X P，et al. Computational fluid dynamics simulation of bubble size and local gas holdup in stirred vessel[J].Journal of Zhejiang University（Engineering Science），2010，44（12）：2396-2415.

[18] SCHILLER L，NAUMANN A. A drag coefficient correlation[J].Vdi Zeitung，1935，77：318-320.

[19] YANG N，CHEN J H，ZHAO H，et al. Explorations on the multi-scale flow structure and stability condition in bubble columns[J]. Chemical Engineering Science，2007，62（24）：6978-6991.

[20] YANG N，CHEN J H，GE W，et al. A conceptual model for analyzing the stability condition and regime transition in bubble columns[J].Chemical Engineering Science，2010，65（1）：517-526.

[21] YANG N，WU Z Y，CHEN J H，et al. Multi-scale analysis of gas–liquid interaction and CFD simulation of gas–liquid flow in bubble columns[J]. Chemical Engineering Science，2011，66（14）：3212–3222.

[22] YANG N. A multi-scale framework for CFD modelling of multi-phase complex systems based on the EMMS approach[J].Progress in Computational Fluid Dynamics，2012，12（2/3）：220–229.

[23] 肖颀. 搅拌釜及鼓泡塔内气液两相流的多尺度模拟[D]. 西安：西安交通大学，2015.XIAO Q. Multi-scale modeling of the gas-liquid flow in mixing tanks and bubble columns[D]. Xi’an：Xi’an Jiaotong University，2015.

[24] 肖颀，杨宁.基于EMMS模型的搅拌釜内气液两相流数值模拟[J].化工学报，2016，67（7）：2732-2739.XIAO Q，YANG N. Numerical simulation of gas-liquid flow in stirred tanks based on EMMS model[J]. CIESC Journal，2016，67（7）：2732-2739.

[25] 蒋雪冬.基于费托合成的气-液及气-液-固鼓泡塔流体力学特性分析[D]. 西安：西安交通大学，2015.JIANG X D. Hydrodynamics analysis of gas-liquid/gas-liquid-solid bubble columns for fischer-tropsch synthesis[D]. Xi’an：Xi’an Jiaotong University，2015.

[26] JIANG X D，YANG N，YANG B L. Computational fluid dynamics simulation of hydrodynamics in the riser of an external loop airlift reactor[J]. Particuology，2016，27：95-101.

[27] XU T T，JIANG X D，YANG N，et al. CFD simulation of internal-loop airlift reactor using EMMS drag model[J].Particuology，2015，19：124-132.

[28] TOMIYAMA A，KATAOKA I，ZUN I，et al. Drag coefficients of single bubbles under normal and microgravity conditions[J]. JSME International Journal，1998，41（2）：472-479.

[29] KHOPKAR A R，TANGUY P A. CFD simulation of gas-liquid flows in stirred vessel equipped with dual Rushton turbines: influence of parallel，merging and diverging flow configurations[J]. Chemical Engineering Science，2008，63（14）：3810-3820.

[30] 王卫京. 气液两相搅拌槽的数值模拟与实验研究[D].北京：中国科学院过程工程研究所，2002.WANG W J. Numerical simulation and experimental investigation on gas-liquid flow in a stirred tank[D]. Beijing：Institute of Process Engineering，Chinese Academy of Sciences，2002.

Experimental study and CFD simulation of gas-liquid flow in a stirred tank using the EMMS drag model

LI Xinju1，2，GUAN Xiaoping2，YANG Ning2，LIU Mingyan1
（1School of Chemical Engineering and Technology，Tianjin University，Tianjin 300350，China；2State Key Laboratory of Multiphase Complex Systems，Institute of Process Engineering，Chinese Academy of Sciences，Beijing 100190，China）

The characteristics of local gas-liquid dispersion characteristics in a stirred tank of Rushton impellers were studied by experiments and CFD simulation. The local gas holdup distribution was measured by using a double conductance probe. The gas-liquid flow was modeled by an Eulerian-Eulerian two-fluid model along with thek-εturbulence mixture model. Effects of rotational speed on the local gas holdup distribution in the upper and lower circulation zone were studied. The experiments showed that the effect of rotational speed on gas holdup distribution in the upper circulation zone was larger than that in the lower circulation zone，and the gas holdup increased with increasing rotational speed. The prediction of the TOMIYAMA drag model and the DBS-Local drag model based on the EMMS theory was compared. The results showed that the DBS-Local drag model could reasonably predict the local gas holdup distribution under different rotational speeds. The TOMIYAMA drag model can only reasonably predict the local gas holdup distribution under lower rotational speeds（N=140r/min，280r/min）. It cannot predict the gas bubbles near the tank wall of the lower circulation region，and underestimated the gas holdup in the upper recirculation region at higher rotational speeds（420r/min，560r/min）.

stirred tank；gas-liquid flow；conductivity probe；energy-minimization multi-scale；computational fluid dynamics

TQ021.1

A

1000–6613（2017）11–4000–10

10.16085/j.issn.1000-6613.2017-0051

2017-03-13；修改稿日期2017-04-19。

国家重点研究开发计划（2017YFB0602500）及国家自然科学基金（91434121，91634203）项目。

李新菊（1990—），女，硕士研究生。E-mail：xjli@ipe.ac.cn。

联系人：杨宁，博士，研究员，主要从事化工及过程工业中多相反应器的多尺度计算流体力学及过程模拟。E-mail：nyang@ipe.ac.cn。