钢铁企业蒸汽动力系统优化

高金彤，倪团结，张琦

（东北大学国家环境保护生态工业重点实验室，辽宁 沈阳 110819）

钢铁企业蒸汽动力系统优化

高金彤，倪团结，张琦

（东北大学国家环境保护生态工业重点实验室，辽宁 沈阳 110819）

随着能源短缺与环境污染问题日益紧迫，钢铁企业所面临的节能减排压力也越来越大，合理的生产方案对降低企业运行成本、减少污染物排放起着重要的作用。本文针对钢铁企业蒸汽动力系统，采用锅炉效率非线性拟合公式和汽轮机分解模型，考虑能源设备、生产操作以及分时电价等因素，建立了混合整数非线性规划（MINLP）模型，其中，非线性锅炉效率拟合公式的引入使得模型更加符合实际生产状况。模型以蒸汽动力系统运行成本为目标函数，通过优化求解得到各时段燃料和设备负荷的分配方案，与优化前相比，系统总的运行费用减少了4.26%。同时，本文还分析了煤价变化对优化方案的影响以及燃料结构对污染物排放的影响，为企业提高生产效率、降低运行成本及节能减排提供理论依据。

蒸汽动力系统；分时电价；环境；优化；系统工程

钢铁企业属于能源密集型产业，同时也是高能耗高污染行业。随着能源短缺与环境污染问题日益紧迫，钢铁企业所面临的节能减排压力也越来越大[1-2]。对企业来说，片面地追求经济效益，必然导致环境污染加剧，而减少污染物的排放则可能会增加企业的运行成本，因此要寻求解决这一矛盾的折中方案。钢铁企业在生产过程中产生大量的副产煤气[3]，蒸汽动力系统具有消纳和利用部分煤气的能力，通过调整各时段副产煤气及锅炉负荷的分配方案来优化系统运行，也是实现节能减排目标的关键。

近年来，针对钢铁企业蒸汽动力系统优化问题，很多学者进行了大量的研究。AKIMOTO等[4]建立钢铁企业燃料供需预测模型，优化了煤气在煤气柜和锅炉的合理分配。KIM等[5]在此基础上考虑了锅炉效率和煤气柜容量，预测了煤气的供需状况，但仅考虑煤气的优化分配，忽略了蒸汽、电力的耦合关系。张琦等[6]建立了多周期煤气、蒸汽、电力耦合优化分配模型。陈诚亮等[7]建立了一个兼顾蒸汽系统运行配置以及蒸汽系统与余热回收系统联合作用的混合整数非线性模型，但都未考虑分时电价的影响。孟华等[8]针对钢铁企业自备电站锅炉负荷频繁波动的特点，建立了基于环境成本的锅炉负荷多周期优化模型，不过仅考虑锅炉负荷，未对汽轮机发电进行优化。曾玉娇等[9]提出了考虑煤气分配、燃料价格和分时电价的蒸汽系统优化模型，但缺少污染物排放影响因素的研究。SAYYAADI等[10]提出了同时考虑经济和环境因素的多目标优化模型，AGHA等[11]综合热电厂产品生产及公用工程，提出了一种能够减少成本、降低排放的集成优化方法。

在石化企业蒸汽系统方面，李晖等[12]提出了考虑燃料价格、电力价格以及汽电需求不确定性变化的蒸汽系统优化模型。罗向龙等[13-15]建立了考虑环境成本的单目标和多目标优化模型。张鹏飞等[16]针对石化企业蒸汽动力系统的特点建立了蒸汽系统多目标混合整数线性规划（MOMILP）模型，对运行成本和环境成本两个目标统筹优化。由于石化企业锅炉燃料为石油和天然气，而钢铁企业蒸汽动力系统则以煤炭为主要燃料，掺烧部分副产煤气或者以副产煤气为主要燃料，因此要考虑副产煤气的供应量的不确定性及锅炉燃料最低热值问题，锅炉及汽机效率随负荷变化波动大，有必要引入效率随负荷变化的设备模型，同时钢铁企业还存在干熄焦（CDQ）等余热回收利用问题，因此这些研究成果并不能完全适用于钢铁企业，需要针对钢铁企业蒸汽系统在设备负荷、燃料结构以及污染物排放方面的研究。

本文在锅炉效率方面，根据实际生产数据对锅炉效率进行了拟合，得到了非线性的拟合公式，在汽轮机模型方面，采用分解策略来处理多级抽汽式汽轮机[17-18]，针对钢铁企业蒸汽动力系统的特点建立混合整数非线性规划（MINLP）模型，并对钢铁企业污染物排放的影响因素进行了分析，为企业合理安排生产、节能减排提供一定的指导。

1 蒸汽动力系统模型

钢铁企业蒸汽动力系统在满足企业蒸汽电力需求和副产煤气有效利用上起着重要作用，如图1所示，系统设备一般由动力锅炉、余热锅炉及汽轮机组成。根据品质不同，钢铁企业的蒸汽一般可分为中压蒸汽和低压蒸汽：中压蒸汽简称S1，主要是动力锅炉产生蒸汽以及CDQ余热锅炉产汽；低压蒸汽有两种，简称为S2和S3，主要是汽轮机抽汽或背压式汽轮机的排汽、焦化等生产工序中回收的余热蒸汽以及减温减压后的中压蒸汽。在副产煤气利用方面，主要是以企业副产煤气为燃料的燃气锅炉和掺烧煤气的燃煤锅炉的消耗为主，下面分别描述锅炉和汽轮机模型。

图1 钢铁企业能量系统结构图

1.1 锅炉模型

在蒸汽系统中，锅炉以煤为主要燃料，掺烧一些副产煤气。按照实际生产数据可得到锅炉效率和负荷的拟合公式，如式(1)所示。式中，ηb为锅炉效率；Mb为锅炉蒸发量，t/h；为锅炉负荷上下限，其他符号见符号说明，全文同。

1.2 汽轮机模型

蒸汽系统中汽轮机主要有背压式、凝汽式、抽汽背压式和抽汽凝汽式。对于多级抽汽式汽轮机，本文采用分解成多个单级子汽轮机的处理方式，分解后汽轮机的总输出功等于多个子汽轮机输出功的叠加，而各级子汽轮机的输出功等于进出口蒸汽内能减少量乘以等熵效率，分别表示为式(2)和式(3)。Δhn为等熵条件下各级子汽轮机进出口蒸汽比焓降，kJ/kg；Dn,t为t时段各级子汽轮机的蒸汽流量，t/h。

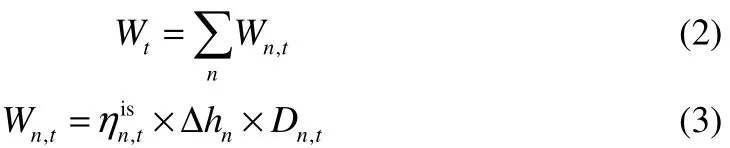
对于汽轮机等熵效率，则按文献[14-15]中公式计算。D为汽轮机进汽量；Dmax为最大进汽量流量，t/h；a0、a1、a2、a3分别为回归参数。

1.3 目标函数

目标函数为运行成本，如式(5)所示，第一部分表示系统使用副产煤气费用、外购煤费用和外购电费用，第二部分表示产汽设备与发电设备的维护费用，第三部分表示外送电收益。

其中，xt为离散变量，表示在t时段是否存在外送电情况，如式(6)所示；ΔPt等于系统在t时段的自产电与电力需求之差。

1.4 约束条件

1.4.1 物料平衡

设备i在t时段内的物料流入量之和等于流出量之和，如式(7)所示。式中Fi,in,t表示t时段内流入设备i的物料流量，t/h；Fi,out,t表示流出的物料流量，t/h。

1.4.2 能量平衡

设备i在t时段内供给能量之和等于输出能量之和加上对外做功，如式(8)所示。hi,in,t表示输入物料比焓，kJ/kg；hi,out,t表示输出物料比焓，kJ/kg；wi,t为设备i的输出功函数。

1.4.3 供需约束

（1）各时段内副产煤气使用量应小于等于供应量，见式(9)。

（2）各时段内各等级蒸汽产量应等于其需求量，见式(10)。

（3）各时段内自产电量与外购电量的和应大于等于电力需求，见式(11)。

1.4.4 设备能力约束

在t时段内，设备i的负荷应在正常范围内，如式(12)。其中，Mi,t为设备负荷；分别表示设备负荷的上下限。

1.4.5 非负约束

模型中各变量都应大于等于0。

2 案例分析

图2为某钢铁企业蒸汽动力系统结构图，每台设备都有两台。通过对该钢铁企业现场调研得到的各设备参数如表1和表2所示，燃料参数如表3所示，表中BFG为高炉煤气，COG为焦炉煤气。系统产S1、S2、S3蒸汽的焓值分别为3330kJ/kg、2920kJ/kg和2796kJ/kg，外购水价格7元/t，分时电价和外送电价格如表4所示，设备的维护成本分别为6元/t和0.06元/(kW·h)。各时段副产煤气供应量、蒸汽和电力需求见表5。模型运行周期为1天，分12时段，每时段2h。围绕该企业实际情况，将蒸汽系统优化模型运用到该案例企业。

2.1 优化结果

目标函数为运行成本，优化变量有设备负荷、燃料消耗、外购电量和外送电量等，使用GAMS软件建模求解，计算环境为2.40 GHz Intel(R) Core(TM)i7-3630QM，模型求解时间小于0.5s。经优化计算，各时段燃料消耗见表6，蒸汽、电力负荷优化分配结果见表7（Power列结果与表5有出入，为舍入误差），优化前后各项费用对比见表8。

表1 锅炉参数

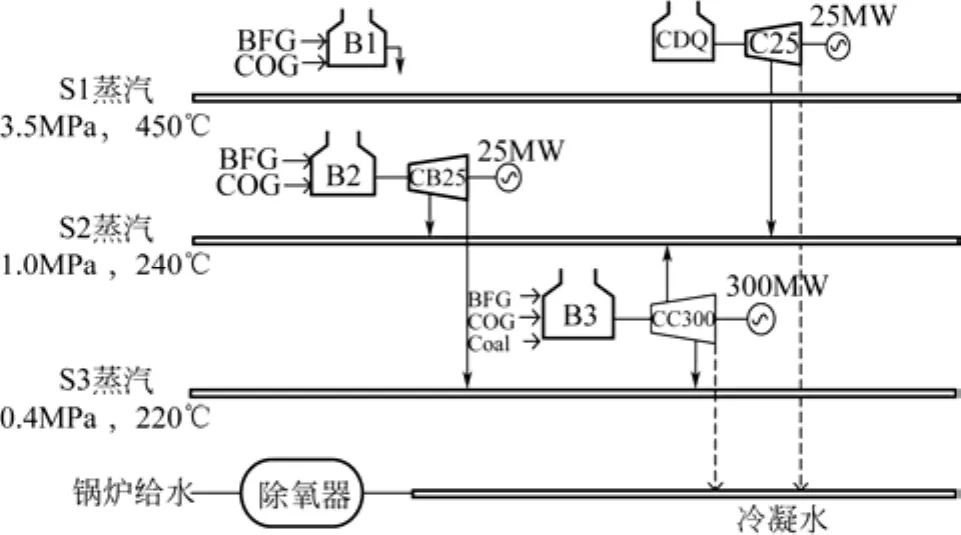
图2 蒸汽动力系统结构图

表2 汽轮机参数

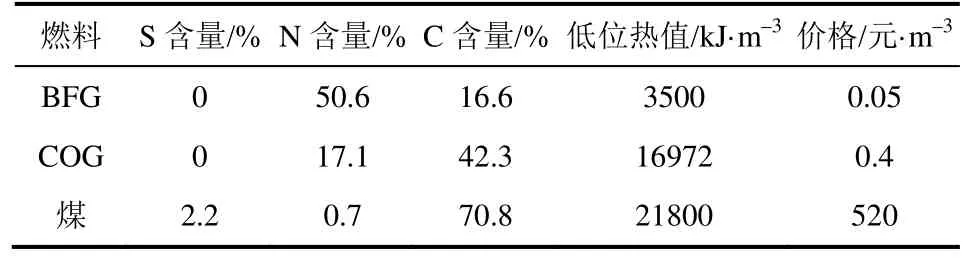
表3 燃料参数

表4 分时电价

从表8中数据可以得出，优化后总的运行费用比优化前减少了166326元，减少量占优化前总费用的4.26%。在各项费用中，外购煤费用相对优化前减少了254196元，副产煤气使用费用增加了110896元，通过比较表5和表6的数据可以看出，系统通过调节B1、B2和B3锅炉的煤气使用量优先利用副产煤气，不足的热量再由燃料煤来补充，减少燃料煤的消耗，达到节能降耗的目的。同时，外购电费用减少了18268元，而外送电收益增加了30203元，从表4和表7中数据能够发现，系统主要在谷电期存在外购电，而在峰电期自发电会增加，在满足产电需求的同时还有一部分电外送，能够根据分时电价调节各时段产电量，制定合理的电网交易计划，减少运行费用。

表5 各时段副产煤气供应量和蒸汽、电力需求

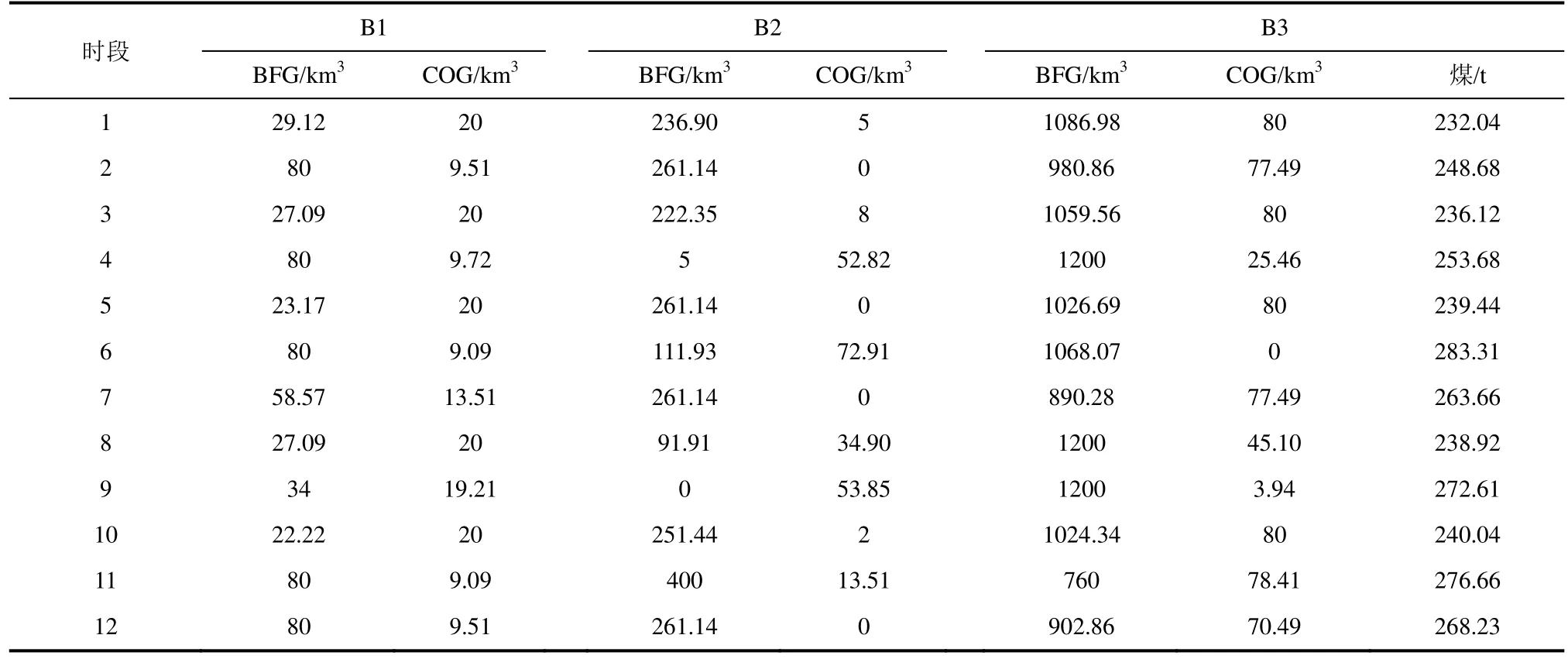
表6 锅炉燃料消耗

表7 蒸汽、电力负荷优化分配结果

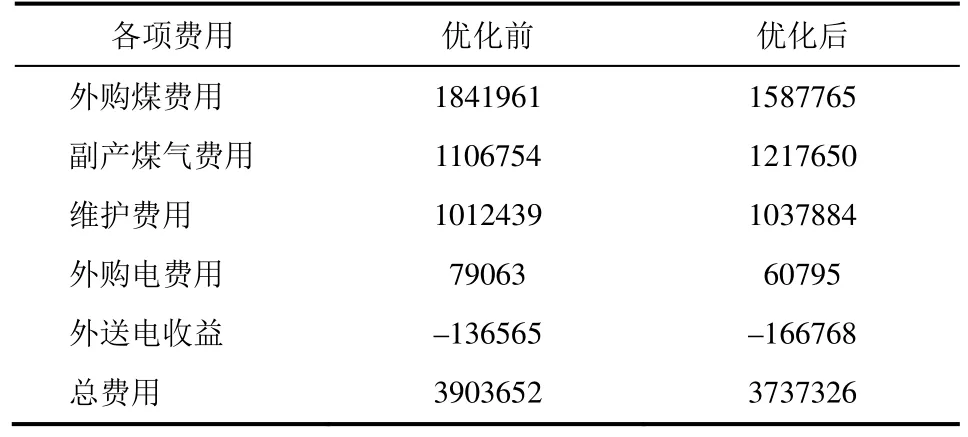
表8 优化前后各项费用对比 单位：元

2.2 煤价变化对优化方案的影响

在对运行成本进行优化时，燃料煤价格同分时电价一样也会对优化结果产生影响。将煤价从300元/t到1000元/t的区间等分成35份，依次进行优化计算，用得到的35组数据绘制成如图3所示的散点图。选取煤价为400元/t、600元/t、800元/t和1000元/t时的外购电与外送电量进行比较，如图4所示，正数表示外购电量，负数表示外送电量，图3中时段1为前一天23:00至第二天1:00，时段2为1:00至3:00，依此类推，每个时段2h。

随着煤价升高，发电成本提高，优化后的运行成本也逐渐增加。通过分析图4可以得出，模型能够根据分时电价调节发电量，在谷电期购电，在峰电期外送，增加企业的经济效益。其次，随着煤价升高系统外购电量增加，自发电量减少，但仍保持谷电期外购、峰电期外送的总体趋势。这说明模型能够获得不同煤价下最合理的电网交易计划，体现了模型的实用性。

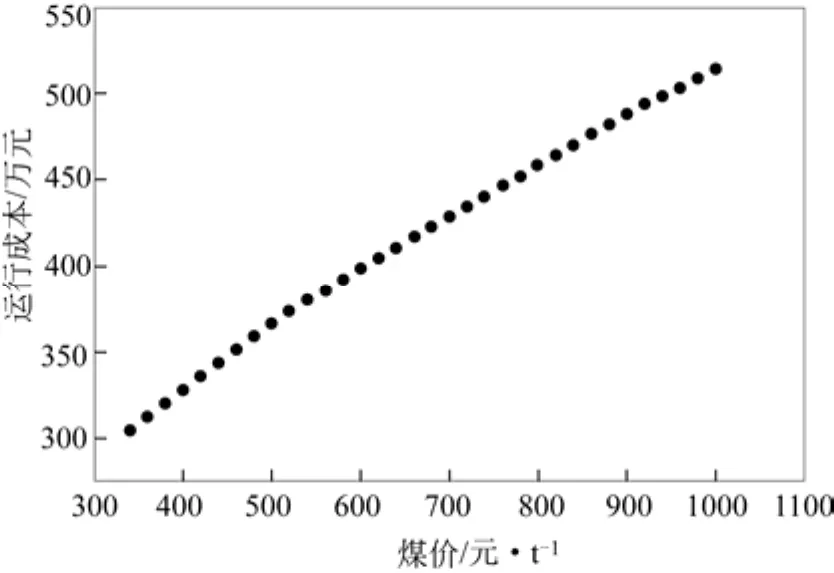
图3 煤价-运行成本散点图

图4 不同煤价下电网交易

2.3 燃料结构对污染物排放的影响

钢铁企业生产过程中排放的污染物有CO2、SO2和NOx，利用式(13)计算可得各时段污染物排放量，式中Gt,p表示污染物排放量；为各时段燃料消耗量，表示每单位燃料燃烧后的污染物排放量；下角标p表示污染物种类。

根据表3燃料参数及表6燃料分配方案，由式(13)计算可得优化方案的污染物排放量，在整个周期内系统产生了15407.70t CO2、7.52t SO2以及137.92t NOx。其中SO2全部来自燃料煤，CO2有49.62%来自BFG，NOx中则有89.63%来自BFG。此时BFG和COG的利用率都为100%，而系统提供BFG和COG的数量比为13.7∶1，BFG具有数量多、热值低、燃烧后CO2和NOx产生量大的特点，因此针对BFG使用量对污染物排放的影响进行分析，利用所建模型在BFG利用率从30%到100%之间每隔10个百分点进行一次优化计算，每次优化所得污染物排放量变化如图5所示，相应的COG利用率及煤耗如图6所示。

图5 不同BFG利用率下的污染物排放量

图6 不同BFG利用率下COG利用率及煤耗

在限制BFG使用量的情况下对运行成本进行优化，此时COG利用率仍为100%不变，系统通过增加煤耗来弥补燃料的不足，运行费用会有所提高。而在污染物排放量方面，BFG利用率从100%减少到30%后，CO2排放量从15407.70t减少到13990.69 t，NOx从137.92t减少到59.13t，SO2从7.52t增加到11.65t。在钢铁企业实际生产中，可根据污染物排放限额制定合理的燃料分配方案，在满足污染物排放要求的前提下，尽可能充分利用副产煤气，实现企业节能减排目标。

3 结论

本文针对钢铁企业蒸汽动力系统，综合原料费用、设备维护费用、外购电费用以及外送电收益，采用锅炉效率非线性拟合公式和汽轮机分解模型，建立了完善的优化调度模型，并通过GAMS软件进行建模求解。从得到的燃料消耗和负荷分配方案可以看出，优化后系统副产煤气利用率提高，煤耗降低，同时电网交易方案更为合理，运行成本降低，从而增加了企业的经济效益。此外，本文分析了煤价变化对运行费用和自发电的影响，在不同煤价下模型都能够根据分时电价合理安排发电机组出力，在谷电期外购，峰电期外送，体现了模型的实用性。由于BFG数量多、热值低、燃烧后CO2和NOx产生量大，因此分析BFG利用率对污染物排放量的影响，在实际生产中可根据污染物排放限额调节副产煤气和燃料煤的使用，实现节能减排目标。

符号说明

a0，a1，a2，a3——回归参数，量纲为1

C——运行成本，元

C1——拟合公式系数，h2/t2

C2——拟合公式系数，h/t

C3——拟合公式系数，量纲为1

Cb——外购电价格，元/(kW·h)

Ccoal——燃料煤价格，元/t

Cg——煤气使用费用，元/m3

Cm——设备维护费用，元/m3或元/(kW·h)

Cs——外送电价格，元/(kW·h)

D——汽轮机进汽量，t/h

Dmax——汽轮机最大进汽量，t/h

Fcoal——燃料煤消耗量，t/h

Fg——煤气消耗量，m3/h

——锅炉最大燃烧煤气量，m3/h

Gp——污染物排放量，t

hin，hout——流入/流出设备物料的比焓，kJ/kg

Δh——蒸汽实际焓降，kJ/t

Δhis——蒸汽等熵焓降，kJ/t

i——设备

M——设备负荷，t/h

Mmin，Mmax—— 设备负荷上下限，t/h

Qin，Qout—— 流入/流出设备的物料流量，t/h

P—— 产电量，MW

Pb—— 外购电量，MW

Pn—— 电力需求，MW

—— 每单位燃料燃烧后的污染物排放量，t

Tsat,in—— 进汽压力下的饱和温度，℃

W—— 汽轮机输出功，MW

w—— 功函数

x—— 外送电收益系数

ηb—— 锅炉效率

—— 汽轮机等熵效率

下角标

n—— 各级子汽轮机

t—— 时段

[1] ZHANG Y J，HAO J F，SONG J. The CO2emission efficiency,reduction potential and spatial clustering in China’s industry:evidence from the regional level[J]. Applied Energy，2016，174（14）：213-223.

[2] KARALI N，XU T，SATHAYE J. Developing long-term strategies to reduce energy use and CO2emissions——analysis of three mitigation scenarios for iron and steel production in China[J]. Mitigation &Adaptation Strategies for Global Change，2016，8（11）：1-21.

[3] HE F，ZHANG Q Z，LEI J S，et al. Energy efficiency and productivity change of China's iron and steel industry：accounting for undesirable outputs[J]. Energy Policy，2013（54）：204-213.

[4] AKIMOTO K，SANNOMIYA N，NISHIKAWA Y，et al. An optimal gas supply for a power plant using a mixed integer programming model[J]. Automatica，1991，27（3）：513-518.

[5] KIM J H，YI H S，HAN C. A novel MILP model for plantwide multiperiod optimization of byproduct gas supply system in the ironand steel-making process[J]. Chemical Engineering Research &Design，2003，81（8）：1015-1025.

[6] 张琦，提威，杜涛，等. 钢铁企业富余煤气-蒸汽-电力耦合模型及其应用[J]. 化工学报，2011，62（3）：753-758.ZHANG Q，TI W，DU T，et al. Coupling model of gassteam-electricity and its application in steel works[J]. CIESC Journal，2011，62（3）：753-758.

[7] CHEN C L，LIN C Y. Design and optimization of steam distribution systems for steam power plants[J]. Industrial & Engineering Chemistry Research，2011，50（13）：8097-8109.

[8] 孟华，王建军，王华，等. 基于环境成本的钢铁企业自备电厂锅炉负荷优化模型[J]. 钢铁研究学报，2013，25（12）：28-34.MENG H，WANG J J，WANG H，et al. Optimal model of boiler load based on environmental costs in self-provided power plant of iron and steel works[J]. Journal of Iron and Steel Research，2013，25（12）：28-34.

[9] ZENG Y J，SUN Y G. Short-term scheduling of steam power system in iron and steel industry under time-of-use power price[J]. Journal of Iron and Steel Research, International，2015，22（9）：795-803.

[10] SAYYAADI H. Multi-objective approach in thermoenvironomic optimization of a benchmark cogeneration system[J]. Applied Energy，2009，86（6）：867-879.

[11] AGHA M H，THERY R，HETREUX G，et al. Integrated production and utility system approach for optimizing industrial unit operations[J]. Energy，2010，35（2）：611-627.

[12] 李晖，孙力，贺高红. 考虑不确定汽电需求的蒸汽动力系统优化设计[J]. 化工学报，2013，64（1）：318-325.LI H，SUN L，HE G H. Design and optimization of steam power system with uncertain steam and power demands[J]. CIESC Journal，2013，64（1）：318-325.

[13] LUO X L，ZHANG B J，CHEN Y，et al. Modeling and optimization of a utility system containing multiple extractions steam turbines[J].Energy，2011，36（5）：3501-3512.

[14] LUO X L，ZHANG B J，CHEN Y，et al. Operational planning optimization of multiple interconnected steam power plants considering environmental costs[J]. Energy，2012，37（1）：549-561.

[15] LUO X L，HU J H，ZHAO J，et al. Multi-objective optimization for the design and synthesis of utility systems with emission abatement technology concerns[J]. Applied Energy，2014，136（24）：1110-1131.

[16] 张鹏飞，赵浩，荣冈，等. 考虑生产成本和环境成本的蒸汽动力系统多目标运行优化[J]. 化工学报，2016，67（3）：715-723.ZHANG P F，ZHAO H，RONG G，et al.Multi-objective optimization for steam power system considering production cost and environmental cost[J]. CIESC Journal，2016，67（3）：715-723.

[17] SHANG Z，KOKOSSIS A. A transhipment model for the optimization of steam levels of total site utility system for multi-period operation[J].Computers & Chemical Engineering，2004，28（9）：1673-1688.

[18] VARBANOV P S，DOYLE S，SMITH R. Modelling and optimization of utility systems[J]. Chemical Engineering Research & Design，2004，82（5）：561-578.

Optimization for steam power system in iron and steel works

GAO Jintong，NI Tuanjie，ZHANG Qi
（State Environmental Protection Key Laboratory of Eco-Industry，Northeastern University，Shenyang 110819，Liaoning，China）

With the issue of energy shortage and environmental pollution becoming more and more urgent，the iron and steel works face increasingly higher pressure of energy saving and emission reduction. A reasonable production plan plays an important role in cost saving and emission reduction.Aiming at the steam power system in iron and steel works，this paper has established a mixed-integer nonlinear programming（MINLP）model that uses fitting formulas of boilers and decomposed model of turbines，considering energy equipments，process operation and time-of-use power price. The application of the nonlinear boiler fitting formulas makes the model more consistent with the actual situation. With the minimization of operating cost，the optimal dispatch scheme of fuels and load at each period were obtained. The total cost has reduced by 4.26 percent compared to the non-optimum one. Two case studies were presented to demonstrate the feasibility of the proposed model. The influence of coal price and fuels was analyzed and the result has proved that this paper is constructive on efficiency improvement，energy conservation and emission reduction.

steam power system；time-of-use power price；environment；optimization；systems engineering

TK01+8

A

1000–6613（2017）11–4301–07

10.16085/j.issn.1000-6613.2017-0237

2017-02-15；修改稿日期2017-07-25。

国家重点研究开发计划项目（2016YFB0601301，2016YFB0601305）。

高金彤（1994—），男，硕士研究生。联系人张琦，博士，副教授，研究方向为系统节能。E-mail：zhangqi@mail.neu.edu.cn。