化工容器碎片引发多米诺效应事故研究历程与展望

陈国华，祁帅，贾梅生，胡昆

（华南理工大学安全科学与工程研究所，广东 广州 510640）

化工容器碎片引发多米诺效应事故研究历程与展望

陈国华，祁帅，贾梅生，胡昆

（华南理工大学安全科学与工程研究所，广东 广州 510640）

化工园区或厂区内，容器爆炸产生的碎片击中临近储罐或装置，可能会引发多米诺效应事故。本文系统分析了国内外有关爆炸碎片产生、飞行、击中及穿透破坏目标容器的相关文献，介绍了爆炸碎片产生阶段与飞行阶段相关随机变量参数的确定方法，以及击中、穿透破坏目标容器的概率模型等方面的研究方法、研究进展，对主要研究内容进行对比。指出碎片类型不全面、击中目标容器判定准则欠精确、目标容器破坏失效准则过于简化、缺乏对爆炸碎片产生概率的研究以及缺乏对目标容器破坏失效后果的研究等不足，提出安全附件等“小型碎片”随机参数的确定、考虑碎片形状体积的击中概率模型、目标容器破坏失效模式与判断准则的改进、爆炸碎片产生概率的计算方法以及目标容器破坏失效后果严重程度的确定是该领域进一步的研究与完善方向。

爆炸碎片；多米诺效应；蒙特卡罗模拟；击中概率模型；破坏失效模式

1984年墨西哥城LPG储运站连锁爆炸事故之后[1]，多米诺效应事故[2-3]逐渐受到重视。每个化工容器都可能因内部爆炸导致的灾难性破裂而产生爆炸碎片，且碎片的抛射距离可以达到几百米甚至上千米[4]。爆炸碎片一旦击中目标容器，可能会刺穿壳体、嵌入壳体或者跳飞，目标容器可能发生穿孔破坏失效或塑性破坏失效，爆炸碎片是引发多米诺效应事故的一类主要因素[5]。当前，关于爆炸碎片抛射引发多米诺效应事故的研究主要集中在碎片击中、破坏目标容器概率评估方面，涉及到化工容器爆炸能量、碎片的尺寸、速度、抛射等，能够为此类事故的管控提供决策支持。

本文主要对爆炸碎片相关随机变量参数确定、爆炸碎片击中破坏目标容器概率的研究历程进行综述，包括下面3个阶段。①碎片产生阶段：爆炸能量，爆炸碎片的数量、形状、质量、速度、角度；②碎片飞行阶段：碎片抛射距离、阻力/升力系数；③碎片撞击阶段：击中目标容器的概率、目标容器破坏失效准则与概率。旨在梳理爆炸碎片引发多米诺效应事故的研究历程与进展，分析当前研究存在的不足，提出展望。

1 碎片产生阶段

1.1 爆炸能量

爆炸能量涉及介质复杂的物理变化以及容器爆炸类型。1959年，BRODE[6]首先提出了适用于理想气体爆炸能量E的公式，如式(1)。

式中，P0为爆炸前气体压强；P1为环境压强；V是容器体积；γ是比热容。

美国化工过程安全中心（CCPS）[7]也采用了这种计算方法。实际上，这是一种粗略的近似计算方法，将气体压强从P0到P1的变化过程视为恒定体积，忽略了实际爆炸过程中诸如容器变形破裂、碎片加速抛射等现象。1988年，BAUM[8]提出了理想气体压力容器、非闪蒸液体压力容器爆炸能量的计算公式，如式(2)、式(3)。

式中，ΔV为爆炸前后液体体积的变化。

同时指出，容器爆炸能量主要作用于3个方面：容器变形、破裂；压缩、置换外部大气；加速爆炸碎片。其中，容器变形、破裂仅消耗约1%的爆炸能量，约20%的能量来加速碎片。1991年，PRUGH[9]采用TNT当量法研究得出了充装易燃液化气体容器发生沸腾液体扩展蒸气云爆炸（BLEVE）时的爆炸能量计算方法，忽略了爆炸前后容器内外的压强变化。此类公式通常是在一些假设的基础上提出的，其准确性有待验证。2005年，荷兰应用科学研究院（TNO）在“黄皮书[10]”中对容器爆炸类型进行了分类，即理想气体压力容器爆炸、非理想气体压力容器爆炸、BLEVE、理想及非理想气体无约束爆炸，含能材料分解以及内部爆炸，并综述了前人关于各种类型爆炸能量计算的关键结论。2013年，BUBBICO等[11]分别将BRODES的方法以及PRUGH的方法应用到氨气、氯气压力容器爆炸能量的计算中，发现BRODES的方法更偏保守，在氨气容器爆炸能量计算中两者更为接近。

容器爆炸压强P0取决于爆炸类型：超压情况下，为最大工作压强×安全系数；物理爆炸情况下，为正常的操作压强[5]。无论历史事故还是实验都难以确定容器爆炸时的真实压强，因此，容器爆炸压强被视为随机变量，在碎片击中概率评估中认为其在容器爆炸压强数值的0.9～1.1倍之间，且服从均匀分布[12]。美国化工过程安全中心将碎片初动能比例因子视为随机变量[7]，其值服从[0.2，0.5]的右三角分布，均值为0.3，这比BAUM提出的爆炸能量的20%用于加速碎片的数值略高。

1.2 爆炸碎片数量

爆炸碎片数量与容器类型、事故场景以及破裂方式（韧性破裂、脆性破裂）密切相关。早期，HOLDEN和REEVES[13]统计分析了106起爆炸碎片抛射危害历史事故，因为实施接近事故场景的实验十分困难，所以他们的统计成为此后学者研究爆炸碎片随机变量参数的重要参考资料。GUBINELLI等[14-15]综合分析了HOLDEN的事故统计、科技文献、事故数据库（MARS等）的143宗爆炸碎片抛射事故，得出卧式储罐事故数量最多，占70.6%，球罐次之，占7.0%。同时，统计了4类事故类型对应产生的碎片数量，如表1。由表1可知，历史事故中由BLEVE引发的碎片抛射占绝大多数，且通常只产生2～3个碎片。NGUYEN等[16]统计研究了31起共产生了76个爆炸碎片的BLEVE历史事故，得出因外部火灾引起的BLEVE平均每起事故产生2.87个碎片，非火灾引起BLEVE的情况下这一数据为2.34个，并指出卧式储罐的尺寸对爆炸碎片的数量没有影响。

表1 不同事故类型与产生的爆炸碎片数量对照[14]

2001年，HAUPTMANNS[12]对46起产生爆炸碎片的事故分析表明，卧式储罐爆炸产生的碎片数量n服从对数正态分布，其均值为0.85516，标准差为0.52448，如式(4)。

式中，Zp,1、Zp,2是[0,1]区间上的2个相互独立的随机数。

该分布在以后的碎片击中概率评估中被广泛采用[16-18]。2009年，NGUYEN等[16]在BAUM的事故统计基础上，绘制了卧式储罐碎片数量频率分布直方图，并依据最大熵原理得出了碎片数量概率密度函数呈指数分布，如式(5)。

2012年，孙东亮等[17]在GUBINELLI事故统计的基础上，进一步研究得出了不同事故场景下的卧式储罐碎片数量概率密度函数，如表2。由于相关历史事故统计有限这一客观原因，依据十分有限的样本得出的碎片数量概率密度函数的准确性仍有待验证。

表2 四种事故场景下的卧式储罐碎片数量概率密度函数[17]

关于球罐爆炸产生的碎片数量，2009年，MÉBARKI等[18]提出，裂纹可能产生于球罐任意位置，爆炸分离的端盖也可能分裂形成平板碎片，以HOLDEN[13]统计的7起球罐爆炸事故分别产生3、4、5、5、6、16、19块碎片的数据为基础，认为球罐碎片数量为[1,19]区间上的均匀分布。以7个样本得出均匀分布的结论欠缺样本支撑，并且没有考虑球罐体积对碎片数量的影响，因为更大的体积表示有更多的裂纹扩展可能性。GUBINELLI等[15]以13起球罐爆炸事故统计为支撑，考虑了球罐体积的影响，提出球罐碎片数量模型，如式(6)。

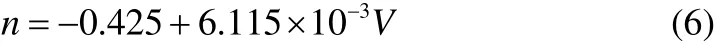
1.3 爆炸碎片形状

爆炸碎片形状取决于容器类型以及裂纹扩展方式。1988年，HOLDEN[19]对卧式储罐工业事故统计分析后发现，共有44块端盖、57块平板以及86块长端盖碎片，所占比例分别为23.5%、30.5%和46%，这一研究成果被后来的碎片击中概率评估所采用[16-18]。2009年，GUBINELLI等[14-15]对133起卧式储罐产生爆炸碎片事故研究后，提出23种容器破裂模式，其中，CV2、CV3、CV7占到所有破裂模式的83.5%，并得出每种破裂模式产生碎片形状的条件概率，如表3。GUBINELLI等的研究在一定程度上提高了确定爆炸碎片数量、形状的准确性，评估对象确定之后，就可以结合可能的事故场景来预估碎片形状及其对应的概率。关于球罐碎片形状，因缺乏历史事故数据，碎片击中概率评估普遍采用20%端盖、80%平板碎片这一比例[20-22]。

当前研究较少关注通过焊缝连接在罐体上的如各种安全部件和人孔等分离抛射产生的碎片击中危害，这些碎片往往在罐体破裂、大量介质泄漏之前就已经由于焊缝断裂失效而被抛射出去，因此通过储罐爆炸能量估算碎片初速度的方法不再适用，需要通过其他方法如开展缩尺寸实验确定抛射速度。

1.4 爆炸碎片质量

化工容器爆炸事故中产生的碎片质量从十几千克到几吨不等，如1993年意大利米拉佐炼油厂的一个56m3的热油储罐发生爆炸事故[23]，共产生41块爆炸碎片，最小的碎片15kg，最大的碎片3860kg。2001年，HAUPTMANNS[12]提出了卧式储罐爆炸碎片质量计算方法，见式(7)、式(8)。2009年，NGUYEN等[16]提出了一种在碎片形状、尺寸、材质确定前提下的碎片质量计算方法，见式(9)。关于球罐，因缺乏碎片质量分布的统计数据，MÉBARKI等[24]的研究均假设每块碎片质量相等。当然，如果碎片其它相关参数已确定，同样可以由式(9)得出碎片质量。

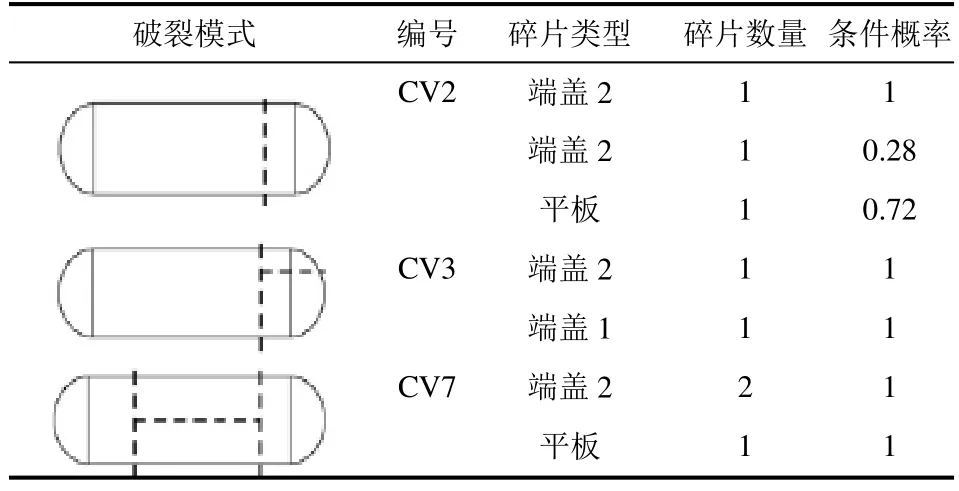
表3 不同破裂模式下各形状碎片产生的条件概率[14-15]

式中，mf为碎片质量；Mt为储罐总质量；k是服从Beta分布的因子。

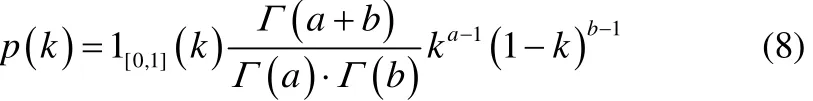
式中，Γ(.)为Gamma函数；a=0.412；b=1.393；，当k∈[0,1]，否则取0。

式中，Vf为碎片体积；ρf碎片密度。

1.5 爆炸碎片速度

BAUM提出的爆炸能量方法[8][见式(2)、式(3)]可以用来估算各种类型储罐产生碎片的速度，但是精确性有所欠缺。之后，BAUM[25-26]开展了一系列小尺寸实验，将端盖用玻璃圈固定在小型卧式储罐上，用加热棒给盛装的水加热，并测量端盖分离时的速度，分布在27.1～87.8m/s。虽然该实验与真实事故场景相比有所差距，但是得出了一些规律，如碎片速度随着质量的减小而增大，与容器充装系数无关，同时提出了1个端盖、2个端盖碎片分离速度的经验公式，计算数据与实测数据呈良好的线性相关性。2008年，GENOVA等[27]基于BAUM实验结论研究得出了端盖抛射速度经验公式，与容器内过热量及端盖质量有关，表达形式更加简洁。但是此类经验公式有一定的局限性，只能用于卧式储罐在BLEVE事故场景下产生1～2个端盖碎片的情况。MÉBARKI等[28]在BAUM提出的爆炸能量计算方法的基础上，着重对碎片初动能比例因子ψ进行了探究，根据BAUM的实验测试数据，依据最大熵原理得到ψ的指数分布关系式，由于缺少球形碎片相关数据，学界普遍将该方法直接用到球罐碎片速度的估算中。2009年，张新梅等[29]推导了一个基于绝热多方过程的爆炸碎片初速度计算公式，认为爆生产物膨胀能量全部转化为碎片动能，结果偏保守。表4为典型碎片初速度计算方法对比。

1.6 爆炸碎片角度

1988年，HOLDEN[19]研究分析了卧式储罐18起BLEVE事故产生的52块碎片的分布，接近60%的碎片集中在罐体轴线60°的范围内，如图1，该结论也间接证明了卧式储罐的碎片种类大多数为端盖。之后，PULA等[30]（2007年）、NGUYEN[16]（2009年）、MÉBARKI等[18]（2009年）等学者提出了卧式储罐碎片水平抛射角度和竖直抛射角度的概率分布，如表5，表中结论均是以Holden的事故统计为基础的，因此样本数量少，准确性稍有欠缺。2014年，TUGNOLI等[31-32]借鉴GUBINELLI对容器破裂模式分类，研究得出了确定性破裂模式下碎片抛射角度的概率密度函数。对于球罐碎片，认为其产生碎片的水平抛射角θ在[0,2π]上均匀分布，竖直抛射角φ在[–π/2, π/2]上均匀分布。

图1 HOLDEN碎片分布统计图[19]

表4 典型碎片初速度计算方法对比

表5 卧式储罐碎片的抛射角度概率密度函数

2 碎片飞行阶段

2.1 阻力/升力系数

碎片抛射的阻力系数CD取决于碎片的几何形状、碎片倾斜角α。1983年，BAKER[33]研究得出了圆片、棒形2种规则几何体水平飞行时的阻力系数，分别为1.17和1.2。2003年，LIU和DENG[34]研究得出了适用性更广泛的阻力系数取值，端盖、长端盖阻力系数在[0.8,1,1]之间均匀分布，平板碎片阻力系数在[0.8,1,1]之间均匀分布。2009年，GUBINELLI等[15]针对容器不同破裂模式产生的不同形状碎片的阻力系数进行研究，得出了7种阻力系数计算公式，其中的关键参数有飞行时间、碎片密度、几何尺寸。GUBINELLI的方法较LIU和DENG的方法适用范围更小，但是对于一个质量、形状已知的碎片其计算结果的精确度更高。

碎片升力是由于碎片上下表面的不对称性产生的。1997年，FRANZINI等[35]提出了升力系数CL的计算方法，如式(10)，并且，倾斜角在[0°,10°]范围之外时，升力系数可忽略不计。在此基础上，为了方便在碎片击中概率评估中应用，2009年，NGUYEN等[16]将端盖、长端盖升力系数视为[0.351,0.468]上的均匀分布，而平板碎片的升力系数可以忽略。事实上，碎片在抛射过程中，阻力系数和升力系数都是随时间变化的函数，在碎片击中概率评估中将其视为一定范围内的均匀分布是经过很大简化的。

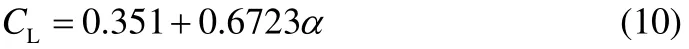
2.2 抛射距离

表6 碎片二维、三维抛射轨迹计算方法对比

2001年，HAUPTMANNS[36]提出了一个卧式储罐发生爆炸事故时，产生的碎片二维抛射轨迹的计算方法，该方法考虑了碎片亚音速范围抛射的空气阻力。2009年，MÉBARKI等[37]提出了碎片三维抛射轨迹的计算方法，考虑了阻力系数与升力系数，忽略了风的作用，分别求出了碎片上升、下降阶段的解。杨玉胜等[20]、LISI等[21]分别根据碎片二维、三维抛射轨迹方程，使用Monte-Carlo法对事故案例进行了模拟。表6为碎片二维、三维抛射轨迹计算方法对比。2009年，钱新明等[22，38]考虑了与地面平行方向的恒定±5m/s风速对球罐BLEVE碎片抛射轨迹的影响，求解MÉBARKI提出的方程，结果表明，碎片抛射距离与无风情况下的分布几乎相同。MÉBARKI和钱新明的研究都将产生碎片的储罐视为一个质点，即假定碎片初始抛射高度和初始抛射水平位移都为零，实际情况中，容器产生碎片的部位是随机的。2010年，陈刚等[39]通过求解MÉBARKI提出的轨迹方程，应用Monte-Carlo法计算了碎片抛射距离的分布函数和概率密度函数，计算了考虑球罐尺寸对碎片抛射距离的影响，与忽略爆炸球罐尺寸的模型对比，击中概率整体偏高。2015年，孙东亮等[40]分别研究了球罐、卧式储罐、立式储罐体积对碎片抛射距离的影响，求解三维轨迹方程，发现在8D（D为容器直径）范围内，碎片击中目标容器的概率要比忽略容器体积时大10%，超过14D的情况下，容器体积才对碎片抛射距离几乎没有影响。在碎片抛射距离的研究中，陈刚和孙东亮得出的结论更符合实际情况，可以在一定程度上提高碎片击中概率评估的准确性。

3 碎片撞击阶段

3.1 击中概率

爆炸碎片击中目标容器的概率是进行爆炸碎片引发多米诺效应事故定量风险评价的重要组成部分。由于爆炸碎片参数的不确定性，在实际计算中，Monte-Carlo法能够采用大量的抽样对随机变量和不确定性进行模拟而得到广泛使用。2001年，HAUPTMANNS[36]对碎片抛射的随机性进行了分析，使用Monte-Carlo模拟求取了碎片对水平目标的击中概率。2004年，GUBINELLI等[41]提出了一个计算已知形状、质量和初始速度的爆炸碎片击中位置和形状已知的目标容器的概率模型，该方法不需要借助Monte-Carlo模拟，求解过程相对简单，但是需要预先确定碎片质量、形状和速度。2007年，PULA等[30]根据目标容器的二维尺寸与碎片形状，计算并划分目标容器易损区域（Vulnerable Area）范围，考虑了2种不同的事故场景（图2），基于碎片二维抛射轨迹方程建立了击中概率模型。2009年，NGUYEN等[16]突破了以往击中概率的局限性，全面考虑了目标容器的三维轮廓，认为碎片抛射轨迹方程与轮廓方程相交就表示击中。钱新明等[22，38]基于碎片三维抛射轨迹，认为碎片落在目标容器的外切立方形区域即算击中目标，并在击中概率模型中考虑了单次模拟中多个碎片的影响。与钱新明的方法相比，NGUYEN模型更具保守性，表7为已有的击中概率模型。当前对击中概率的研究已经考虑了目标容器的尺寸，但是依然忽略了碎片的形状，用碎片三维抛射轨迹与目标容器三维方程相交与否来判断是否击中。

3.2 破坏失效

关于目标容器的破坏失效的研究多集中于穿透失效模式，相关研究从把简单的平面钢板作为研究对象逐渐过度到化工容器。1995年，BUKHAREV等[42]研究了钨质圆柱棒以不同角度击中钢板的破坏模式，并通过实验验证了0°～68°的撞击效果，与理论计算结果取得良好一致性。1998年，KHAN等[43-44]考虑了碎片对目标容器3个方面的影响：①碎片穿透目标容器的可能性ProbA；②碎片携带的能量加热介质导致目标容器破坏失效的可能性ProbB；③碎片与目标容器发生碰撞的可能性ProbC。目标容器在碎片影响下的破坏失效概率由以上3个概率的并集表征。这种方法忽略了3个因素之间的关联性，导致过高地估计了碎片对目标容器的影响，如碎片穿透目标容器、加热介质的前提是要保证击中目标容器。2008年，潘旭海等[45]采用LS-DYNA软件，对爆炸碎片撞击下的立式储罐动力学响应进行了数值模拟，得到了一些定性结论，如立方体碎片的撞击对储罐结构强度的影响大于圆柱形碎片，碎片撞击角度为10°时，储罐强度损失最大。由于爆炸碎片撞击目标容器的原尺寸实验不易实现，数值模拟是研究目标容器破坏失效的有力方法，但是也存在如有限元模型的正确性验证、碎片几何形状理想化处理的有效性等问题，通过数值模拟得出碎片撞击下目标容器破坏失效的相关规律性、定性的结论可以做参考，定量结论参考意义不大。

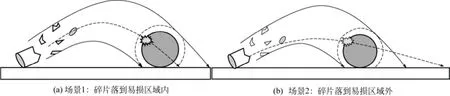
图2 爆炸碎片影响目标容器场景[30]

表7 碎片击中目标容器概率模型对比

目前，关于爆炸碎片撞击下目标容器的破坏失效研究还很少。2009年，NGUYEN等[16]认为在MÉBARKI等[46]关于柱形碎片撞击破坏金属平板模型的基础上，认为当碎片撞击深度达到容器壁厚，或者撞击后的残余壁厚小于某个临界值时就会导致目标容器破坏失效，由此建立了碎片对目标容器的破坏概率模型。2012年，陈刚等[47]认为临界残余壁厚的求取涉及复杂的局部应力分析，并且随着容器材料、壁厚等因素而变化，求解困难，因此借鉴李思源等[48-49]基于容器壳体损失面积安全性评价的思路，提出了基于临界剩余强度系数的容器在爆炸碎片击中影响下的破坏失效判断准则。剩余强度系数（RSF）是指材料强度极限σb与结构在载荷作用下的工作压力σw之比，容器壳体所受应力等于1.5倍的屈服极限σs时的剩余强度系数即为临界剩余强度系数（RSFcr），并据此提出破坏失效模型。2015年，SALZANO等[50]研究了碎片撞击下包括混凝土结构、砖墙结构、钢制储罐在内的广义目标装置设备破坏失效的情况，分别推导了2个依据碎片质量划分的撞击深度公式，认为撞击深度大于目标装置设备厚度即发生穿透失效，该方法没有考虑碎片形状的影响，表8为3种目标容器破坏失效模型对比。2016年，孙东亮等[51]以上海某石化公司的含4个球罐的罐区为研究对象，基于NGUYEN的破坏失效模型，使用Monte-Carlo法探索了爆炸碎片引发多重多米诺效应事故的概率，结果表明发生一次、二次、三次多米诺效应事故的概率分别为10–7、10–11、10–15。NGUYEN、陈刚和SALZANO的方法都将撞击深度视为在容器原有结构厚度上的直接减薄，实际情况中，爆炸碎片撞击目标容器，罐壁会产生明显的局部凹陷变形，并且在短时高强度冲击载荷作用下，容器材料的屈服极限也会因应变率效应而增大，在进行碎片穿透破坏目标容器相关研究中采用静力学中的屈服极限已经不再合适，应根据碎片撞击速度确定应变率的数量级，通过实验研究得出容器材料在对应应变率数量级下的屈服极限。

4 当前研究不足与展望

（1）碎片类型研究不够全面。除了当前关注的罐体本身破裂产生的“大型碎片”，因焊缝断裂抛射的安全附件和人孔等“小型碎片”、受冲击波损毁的混凝土碎块等非罐体碎片都是需要探索研究的。

表8 碎片撞击下目标容器破坏失效模型对比

（2）碎片击中目标容器判断准则欠精确。当前采用碎片抛射轨迹与目标容器相交与否来判断是否击中，当碎片体积较大时，判定是否击中目标容器不宜再用这种方法，而应该充分考虑碎片的体积形状。

（3）目标容器破坏失效模式过于单一且简化。除了当前关注的碎片穿透破坏目标容器的情况，碎片撞击导致容器失稳倾倒、碎片切断容器支柱或连接管线导致的破坏失效以及多个碎片击中容器的叠加效应等都是需要研究的。此外，当前的穿透失效模型都将撞击深度视为在容器原有结构厚度上的直接减薄，忽视了器壁在冲击载荷下的应变率效应、局部凹陷等现象，可以通过实验来进一步研究导致事故升级的目标容器穿透破坏失效模型。

（4）缺乏对容器爆炸产生碎片概率的研究。无论是否采用Monte-Carlo模拟得出碎片击中目标容器的概率，都是假定化工容器一定发生爆炸产生碎片，即Pgen=1，当前的研究偏向于碎片产生之后的抛射距离、击中破坏目标容器的概率方面，缺乏对碎片产生概率的研究。在定量风险评价中，Pgen也是值得探索的，为从源头控制提供指导，实现本质安全。

（5）缺乏对目标容器破坏失效后果的研究。爆炸碎片击中破坏目标容器的概率研究是定量风险评价的一方面，也是当前研究比较成熟的一部分。关于碎片撞击目标容器的事故后果，如导致目标容器不同程度的泄漏，高能碎片对介质加热引发的火灾等可以作为未来的研究方向。

5 结论

本文从化工容器爆炸碎片产生阶段和飞行阶段相关随机变量参数的确定、击中破坏目标容器的概率等方面对国内外研究现状进行了归纳、总结、评述；指出了当前研究存在的不足，如碎片类型不全面、击中目标容器判断准则欠精确、目标容器破坏失效模式过于单一且简化、缺乏对容器爆炸产生碎片概率的研究以及缺乏对目标容器破坏失效后果的研究等；提出了进一步研究重点及建议供参考，如安全附件等“小型碎片”随机参数的确定、考虑碎片形状体积的击中概率模型、目标容器破坏失效模式与判断准则的改进、爆炸碎片产生概率的计算方法以及目标容器破坏失效后果严重程度的确定等。

[1] PIETERSEN C M.Analysis of the LPG-disaster in mexico city[J].Journal of Hazardous Materials，1988，20（1）：85-107.

[2] COZZANI V，GUBINELLI G，ANTONIONI G，et al.The assessment of risk caused by domino effect in quantitative area risk analysis[J].Journal of Hazardous Materials.2005，127（1/2/3）：14-30.

[3] COZZANI V，TUGNOLI A，SALZANO E.Prevention of domino effect: from active and passive strategies to inherently safer design.[J].Journal of Hazardous Materials，2007，139（2）：209-219.

[4] COZZANI V，TUGNOLI A，SALZANO E.The development of an inherent safety approach to the prevention of domino accidents[J].Accident Analysis and Prevention，2009，41（6）：1216-1227.

[5] NECCI A，COZZANI V，SPADONI G，et al.Assessment of domino effect：state of the art and research Needs[J].Reliability Engineering and System Safety，2015，143:3-18.

[6] BRODE H L.Blast wave from a spherical charge[J].Physics of Fluids，1959，2（2）：217-229.

[7] Centre for Chemical Process Safety.Guidelines for chemical process quantitative risk analysis[M].New York：American Institute of Chemical Engineers，2000.

[8] BAUM M R.Disruptive failure of pressure vessels：preliminary design guidelines for fragment velocity and the extent of the hazard zone[J].Journal of Pressure Vessel Technology，1988，110（2）：168-176.

[9] PRUGH R W.Quantitative evaluation of" Bleve" hazards[J].Journal of Fire Protection Engineering，1991，3（1）：9-24.

[10] VEN DEN BOSCH C J H，Weterings R.Methods for the calculation of physical effects (Yellow Book)[M].Hague：Committee for the Prevention of Disasters，2005.

[11] BUBBICO R，MAZZAROTTA B.Analysis and comparison of calculation methods for physical explosions of compressed gases[C]//PIERUCCI S.AIDIC Conference Series.Italy：The Italian Association of Chemical Engineering，2013，11：133-138.

[12] HAUPTMANNS U.A procedure for analyzing the flight of missiles from explosions of cylindrical vessels[J].Journal of Loss Prevention in the Process Industries，2001，14（5）：395-402.

[13] HOLDEN P L，REEVES A B.Fragment hazards from failures of pressurized liquefied gas vessels[C]//IchemE Symposium Series.The UK：Safety and Reliability Directorate，1985，93：205-220.

[14] GUBINELLI G，COZZANI V.Assessment of missile hazards:Identification of reference fragmentation patterns[J].Journal of Hazardous Materials，2009，163（2）：1008-1018.

[15] GUBINELLI G，COZZANI V.Assessment of missile hazards:evaluation of the fragment number and drag factors.[J].Journal of Hazardous Materials，2009，161（1）：439-449.

[16] NGUYEN Q B，MÉBARKI A，SAADA R A，et al.Integrated probabilistic framework for domino effect and risk analysis[J].Advances in Engineering Software，2009，40（9）：892-901.

[17] SUN D L，JIANG J C，ZHANG M G，et al.Parametric approach of the domino effect for structural fragments[J].Journal of Loss Prevention in the Process Industries，2012，25（1）：114-126.

[18] MÉBARKI A，MERCIER F，NGUYEN Q B，et al.Structural fragments and explosions in industrial facilities. Part I: Probabilistic description of the source terms[J].Journal of Loss Prevention in the Process Industries，2009，22（4）：408-416.

[19] HOLDEN P L.Assessment of missile hazards: review of incident experience relevant to major hazard plant[M].London：UKAEA Safety and Reliability Directorate，1988.

[20] 杨玉胜，吴宗之.储罐爆炸碎片最可能抛射距离的Monte-Carlo（蒙特卡罗）数值模拟[J].中国安全科学学报，2008，18（3）：15-21.YANG Y S，WU Z Z.Monte-Carlo numerical simulation on the most probable flight distance of fragments from explosion of storage tanks[J].China Safety Science Journal，2008，18（3）：15-21.

[21] LISI R，CONSOLO G，MASCHIO G，et al.Domino effects due to the projection of fragments: estimation of the impact probability using a Monte Carlo simulation[J].Chem. Eng.Trans.，2014，36：361-366.

[22] 钱新明，徐亚博，刘振翼.球罐BLEVE碎片抛射的Monte-Carlo分析[J].化工学报，2009，60（4）：1057-1061.QIAN X M，XU Y B，LIU Z Y.Monte-Carlo analysis of fragments projectile from spherical tank BLEVE[J].CIESC Journal，2009，60（4）：1057-1061.

[23] LISI R，CONSOLO G，MASCHIO G，et al.Estimation of the impact probability in domino effects due to the projection of fragments[J].Process Safety and Environmental Protection，2014，93：99-110.

[24] MÉBARKI A，JEREZ S，MATASIC I.Explosions and structural fragments as industrial hazard：domino effect and risks[J].Procedia Engineering，2012，45：159-166.

[25] BAUM M R.Failure of a horizontal pressure vessel containing a high temperature liquid: the velocity of end-cap and rocket missiles[J].Journal of Loss Prevention in the Process Industries，1999，12（2）：137-145.

[26] BAUM M R.The velocity of large missiles resulting from axial rupture of gas pressurised cylindrical vessels[J].Journal of Loss Prevention in the Process Industries，2001，14（3）：199-203.

[27] GENOVA B，SILVESTRINI M，TRUJILLO F J L.Evaluation of the blast-wave overpressure and fragments initial velocity for a BLEVE eventviaempirical correlations derived by a simplified model of released energy[J].Journal of Loss Prevention in the Process Industries，2008，21（1）：110-117.

[28] MÉBARKI A，NGUYEN Q B，MERCIER F，et al.Reliability analysis of metallic targets under metallic rods impact：towards a simplified probabilistic approach[J].Journal of Loss Prevention in the Process Industries，2008，21（5）：518-527.

[29] ZHANG X M，CHEN G H.The analysis of domino effect impact probability triggered by fragments[J].Safety Science，2009，47（7）：1026-1032.

[30] PULA R，KHAN F I，VEITCH B，et al.A model for estimating the probability of missile impact：missiles originating from bursting horizontal cylindrical vessels[J].Process Safety Progress，2007，26（2）：129–139.

[31] TUGNOLI A，GUBINELLI G，LANDUCCI G，et al.Assessment of fragment projection hazard：probability distributions for the initial direction of fragments[J].Journal of Hazardous Materials，2014，279：418-427.

[32] TUGNOLI A，MILAZZO M F，LANDUCCI G，et al.Assessment of the hazard due to fragment projection: a case study[J].Journal of Loss Prevention in the Process Industries，2013，28（6）：36-46.

[33] BAKER W E.Explosion hazards and evaluation[M].Amsterdam：Elsevier Scientific Pub.Co.，1983.

[34] LIU P，DENG X.Experimental investigation of aerodynamic characteristics on slender bodies at high angles of attack[J].Canadian Aeronautics and Space Journal，2003，49（1）：31-40.

[35] FRANZINI J B，FINNEMORE E J，DAUGHERTY R L.Fluid mechanics with engineering applications[M].McGraw-Hill Companies，1997.

[36] HAUPTMANNS U.A Monte-Carlo based procedure for treating the flight of missiles from tank explosions[J].Probabilistic Engineering Mechanics，2001，16（4）：307–312.

[37] MÉBARKI A，NGUYEN Q B，MERCIER F.Structural fragments and explosions in industrial facilities：Part Ⅱ——Projectile trajectory and probability of impact[J].Journal of Loss Prevention in the Process Industries，2009，22（4）：417-425.

[38] 钱新明，徐亚博，刘振翼.球罐BLEVE碎片抛射的危害性研究[J].高压物理学报，2009，23（5）：389-394.QIAN X M，XU Y B，LIU Z Y.Research on hazard of fragments from spherical tank BLEVE[J].Chinese Journal of High Pressure Physics，2009，23（5）：389-394.

[39] 陈刚，朱霁平，武军，等.爆炸球罐尺寸对抛射碎片击中相邻罐体概率的影响[J].化工学报，2010，61（6）：1599-1604.CHEN G，ZHU J P，WU J，et al.Influence of size of bursting spherical tank on impact probability between fragments and adjacent vessels[J].CIESC Journal，2010，61（6）：1599-1604.

[40] SUN D L，JIANG J C，ZHANG M G，et al.Influence of the source size on domino effect risk caused by fragments[J].Journal of Loss Prevention in the Process Industries，2015，35：211-223.

[41] GUBINELLI G，ZANELLI S，COZZANI V.A simplified model for the assessment of the impact probability of fragments[J].Journal of Hazardous Materials，2005，116（3）：175-187.

[42] BUKHAREV Y I，ZHUKOV V I. Model of the penetration of a metal barrier by a rod projectile with an angle of attack[J].Combustion Explosion and Shock Waves，1995，31（3）：362-367.

[43] KHAN F I，ABBASI S A.Models for domino effect analysis in chemical process industries[J].Process Safety Progress，1998，17（2）：107-123.

[44] KHAN F I，ABBASI S A. DOMIFFECT（DOMIno eFFECT）：user-friendly software for domino effect analysis[J].Environmental Modelling & Software，1998，13（2）：163-177.

[45] 潘旭海，徐进，蒋军成，等.爆炸碎片撞击圆柱薄壁储罐的有限元模拟分析[J].南京工业大学学报（自然科学版），2008，30（3）：15-20.PAN X H，XU J，JIANG J C，et al.Finite element simulation analysis on explosion debris impacting thin-wall cylindrical tanks[J].Journal of Nanjing University of Technology（Natural Science Edition），2008，30（3）：15-20.

[46] MÉBARKI A，NGUYEN Q B，MERCIER F，et al.A probabilistic model for the vulnerability of metal plates under the impact of cylindrical projectiles[J].Journal of Loss Prevention in the Process Industries，2007，20（2）：128-134.

[47] 陈刚，朱霁平，武军，等.储罐爆炸抛射碎片对目标容器的破坏概率研究[J].防灾减灾工程学报，2012，32（2）：216-222.CHEN G，ZHU J P，WU J，et al.Damage probability model of target storage tank impacted by explosion fragments[J].Journal of Disaster Prevention and Mitigation Engineering，2012，32（2）：216-222.

[48] 李思源，文斌，唐毅.含球形凹坑球壳构件剩余强度系数的计算[J].压力容器，2009，26（3）：37-42.LI S Y，WEN B，TANG Y.The calculation of remaining strength factor of spherical shell components with spherical pits[J].Pressure Vessel Technology，2009，26（3）：37-42.

[49] 李思源，文斌，唐毅，等.含凹坑圆柱壳的剩余强度系数[J].压力容器，2009，26（7）：18-28.LI S Y，WEN B，TANG Y.The remaining strength factor of cylindrical shells with pits[J].Pressure Vessel Technology，2009，26（7）：18-28.

[50] SALZANO E，BASCO A.Simplified model for the evaluation of the effects of explosions on industrial target[J]. Journal of Loss Prevention in the Process Industries，2015，37：119-123.

[51] SUN D L，JIANG J C，ZHANG M G，et al.Investigation of multiple domino scenarios caused by fragments[J].Journal of Loss Prevention in the Process Industries，2016，40：591-602.

Research on Domino effect accident caused by the fragments of chemical vessels in retrospect and prospect

CHEN Guohua，QI Shuai，JIA Meisheng，HU Kun
（Institute of Safety Science & Engineering，South China University of Technology，Guangzhou 510640，Guangdong，China）

The adjacent vessels may be impacted and/or destroyed by blast fragments in chemical parks or plants，which leads to Domino effect accident. By analyzing and reorganizing the research on generation and projection of fragments，the impact and damage probability model of target vessels in literature and the determination of random variables during the periods of generation and projection，the impact and the damage probability model are introduced and specifically compared. The inadequacies of current research are pointed out，including that the type of fragments is not comprehensive，the criterion of fragments impacting target vessels is less accurate，the failure criterion of target vessels is too simple，the generating probability of fragment from explosion is lack，and the consequence severity of damaged vessels is lack. It is suggested that the determination of random variables of “small fragments” like safety accessories，the impact probability model considering the shape and volume of fragment，the improved damage model and criterion of failure model of target vessels，the generating probability of fragment from explosion and the consequence severity of damaged vessels should be further researched in the future.

blast fragment；Domino effect；Monte-Carlo simulation；impact probability model；damage pattern

TQ086

A

1000–6613（2017）11–4308–10

10.16085/j.issn.1000-6613.2016-2361

2017-12-19；修改稿日期2017-02-13。

国家自然科学基金项目（21576102）。

及联系人：陈国华（1967—），男，教授，博士生导师，主要研究方向为工业安全与风险评价技术及管理信息系统、过程装备安全可靠性及风险评价技术。E-mail：mmghchen@126.com。