椭圆形均匀带电环中心点电势的数值计算

金玲玲，敬晓丹，袁 泉

（辽宁工业大学 理学院，辽宁 锦州 121001）

椭圆形均匀带电环中心点电势的数值计算

金玲玲，敬晓丹，袁 泉

（辽宁工业大学 理学院，辽宁 锦州 121001）

利用直角坐标系下的椭圆参数方程推导出椭圆形均匀带电环中心点的电势计算的积分形式。根据数值分析中的Netwon-Cotes公式，计算出椭圆形均匀带电环中心点的电势值，并由此得到了均匀带电圆环中心点处的电势，为其他形状的均匀带电曲线的电势数值计算提供了一种方法。

电势叠加原理；椭圆带电环；数值计算

根据大学物理学中的电势的定义和电势叠加原理，比较容易计算均匀带电圆环中心处的电势，而更为普遍的椭圆形均匀带电环中心处的电势和场强的计算[1-2]标系下对弧长积分，由于被积函数复杂或不容易找到原函数，需要进行数值积分[3]的计算。本文拟用直角坐标系下的椭圆参数方程，推导出椭圆形均匀带电环在中心处的电势的计算表达式，并利用数值积分的公式，计算出中心处的电势，并根据结果讨论得出圆心处的电势。

1 理论计算

如图1所示，椭圆形均匀带电环的带电量为q，半长轴为a，半短轴b(a＞b)。根据电势叠加原理，取带电线密度为λ=q/π(a+b)，在(x,y)处的微元 dl，带电量为dq=λdl，在椭圆的中心处o产生的电势为：

图1 椭圆形均匀带电环

整个椭圆上的电荷q在中心点 o产生的电势为：

直角坐标系下，根据椭圆参数方程x=acosθ，y=bsinθ(0≤θ＜2π)，微元：

微元到中心点的距离：

将dl、r代入式(1)、式(2)并化简得：

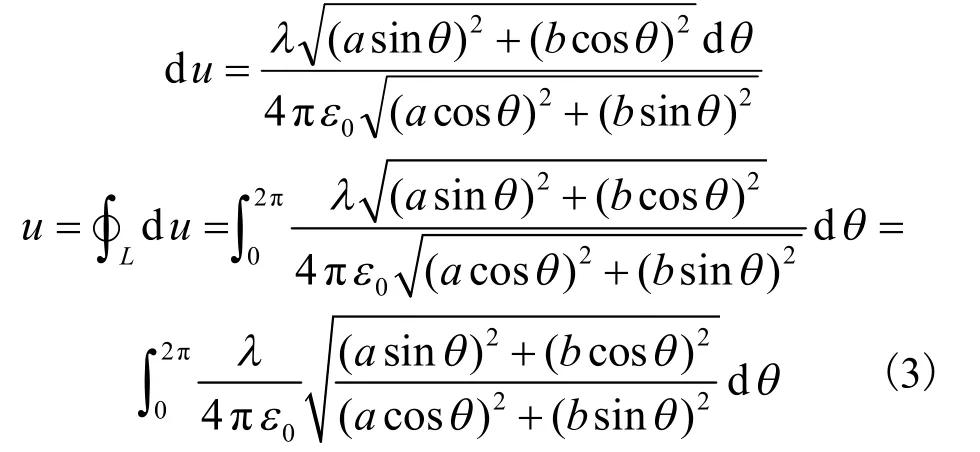
由椭圆形均匀带电环的对称性可知，整个椭圆形带电环产生的电势等于第一象限的1/4椭圆弧长产生的电势的4倍，对式(3)积分得：

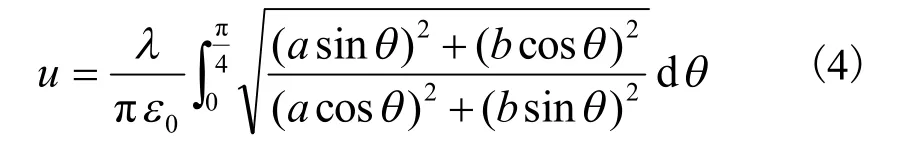
由于式(4)的原函数不容易找到或者非常复杂，可以利用数值分析中的Newton-Cotes公式进行计算。在θ=[0，π/2]内采用 5个等距插值节点θ0、θ1、θ2、θ3、θ4，θ=0，π/8，2π/8，3π/8，4π/8；将[0，π/2]区间4等分，即n=4的Newton-Cotes数值积分公式：

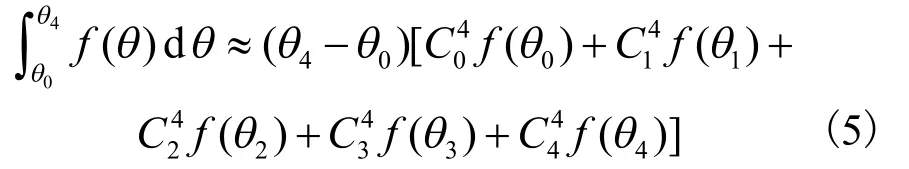
其中：

根据式(5)的Newton-Cotes公式：

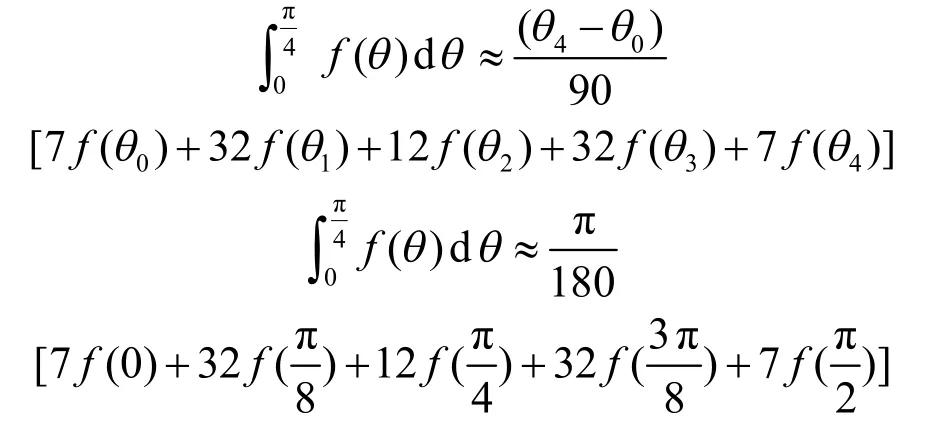
中心点处的电势：

式(6)推出的椭圆形均匀带电环中心点处的电势的数值计算公式，对于b/a比值不是很小(保证点电荷的条件成立)的均匀带电环的电势都可以求出数值解。

若椭圆带电环的半长轴和半短轴相等，即a=b=R，式(6)中的u=q/4πε0R，这便是熟知的均匀带电圆环在圆心处的电势计算公式。

2 结论

分别利用直角坐标系下的椭圆方程，根据电势叠加原理，推导出了椭圆形均匀带电环中心点的电势计算式。为提高计算精度，利用n=4的Newton-Cotes积分公式，对椭圆形均匀带电环中心点的电势进行数值计算，并进一步得到均匀带电圆环圆心的电势。将数值积分公式应用到电势叠加原理的计算，解决了电势计算过程中不容易找到原函数或原函数较复杂时均匀带电环的电势积分计算问题。

[1]张之翔.均匀带电圆环的电场强度[J].大学物理,2012(5): 14-16.

[2]穆良柱,陈熙谋.毕奥-萨伐尔定律建立过程中的数学分析[J].大学物理,2008(11): 5-7.

[3]李庆扬,王能超,李大义.现代数值分析[M].北京: 高等教育出版社,1995.

Numerical Calculation of Electric Potential at Center Point of Elliptic Circle with Uniform Charge

JIN Ling-ling,JING Xiao-dan,YUAN Quan
（College of Science,Liaoning University of Technology,Jinzhou 121001,China）

The electric potential was derived by using superposition principle under elliptic parameter equation in rectangular coordinates system,which is at center point of elliptic circle with uniform charge.According to Newton-Cotes formula in numerical analysis,the electric potential was calculated by numerical calculation,especially electric potential at the center point of circle was presented as a deduction.

principle of superposition of electric potential; elliptic circle; numerical calculation

O411.3

A

1674-3261(2017)05-0343-02

10.15916/j.issn1674-3261.2017.05.015

2016-11-04

金玲玲(1975-)，女(满族)，辽宁鞍山人，讲师。

责任编校：孙 林