基于增长无源性的切换非线性系统的输出跟踪

庞洪博，柳 硕

（辽宁工业大学 理学院，辽宁 锦州 121001）

基于增长无源性的切换非线性系统的输出跟踪

庞洪博，柳 硕

（辽宁工业大学 理学院，辽宁 锦州 121001）

在每一个子系统的输出跟踪问题都不可解的条件下，利用切换非线性系统增长无源性理论解决一类切换非线性系统的输出跟踪问题。首先,提出了切换非线系统的增长无源概念。这种增长无源性允许存储函数在切换时刻增加。设计状态依赖型切换律使得切换系统是增长无源的。然后，利用再设计的思想解决一类切换非线性系统的输出跟踪问题。另外，通过设计一组输出反馈控制器和复合切换律解决一类级联切换非线性系统的输出跟踪问题。最后，通过仿真例子验证所提出方法的有效性。

增长无源；切换非线性系统；输出跟踪；切换律

20世纪70年代，Willems[1]首次提出无源性概念。一般来讲，无源系统内部消耗的能量不超过外部供给的能量。无源性理论是系统分析与设计的有力工具。但它只适用于一个平衡点的系统。增长无源性是传统无源性的扩展。文献[2-3]从算子的角度提出了增长无源性的概念。文献[4-5]提出状态空间形式的增长无源概念，并建立相应增长无源理论。增长无源性是刻画两条轨线之间能量变化,因此，它不仅可以应用于一个平衡点的系统，而且对于没有平衡点或多平衡点的系统更有意义[6-8]。对于一个增长无源系统，可以通过设计增长无源的控制器使得闭环系统轨线彼此趋近。因此，增长无源理论适合解决输出跟踪及同步化分析等问题[4-5,9-10]。

另一方面，输出跟踪控制是非常典型的控制问题,它广泛存在于航空航天控制、机器人控制等。所谓的输出跟踪控制是指通过设计控制器使得被控对象的输出跟踪一个给定的参考信号。输出跟踪控制问题比镇定问题更具有挑战性。目前，关于非线性系统的输出跟踪控制问题的成果比较成熟[11-13]。

近年来，由于在电力系统[14]、航空航天控制[15]等方面的应用，切换系统得到了广泛的关注。作为一类重要的混杂系统，切换系统是由一族连续时间子系统和决定子系统之间如何切换的规则构成[16]。由于离散动态和连续动态相互作用，切换系统具有更加复杂的行为。因此，切换系统输出跟踪问题也更加困难。目前，解决切换系统输出跟踪问题的方法有很多，如共同李雅普诺夫函数方法[17]、多李雅普诺夫函数方法[18]。平均驻留时间方法[19]。而增长无源仍然可以用于解决切换非线性系统输出跟踪问题[20]。文献[20]利用多存储函数和多供给率方法建立切换非线性系统增长无源理论，提出切换系统增长无源概念。但是它要求存储函数在切换时刻的值是相等的。这是很强的条件。

本文在不要求子系统的增长无源性前提下，设计状态依赖型切换律解决切换非线性系统的输出跟踪问题。与现有结果比较，本文所定义的增长无源概念是文献[20]的推广，它允许存储函数在切换时刻是增加的，且不要求系统输出是共同的。对于级联切换非线性系统，按照所设计的复合切换律，驱动系统和被驱动系统可以异步切换。

1 问题描述与预备知识

考虑如下切换系统：

其中x∈Rn是系统状态；分段连续函数σ（t）:[0,∞）→I=｛1,2,…,M｝称为系统切换信号；假设系统有限时间内切换有限次[16]且状态在切换时刻不跳跃。ui∈Rm是第i个子系统的输入向量；hi(x)∈Rm是连续的输出向量且是连续函数且fi(0)=0对应切换信号的切换序列描述如下：

其中t0是初始时刻，x0是初始状态，且N是非负整数的集合；当时，第ik个子系统工作，即对于任意j∈I：

本文主要解决系统(1)的输出跟踪问题。首先,做如下假设。

假设1存在常数Y以及分段可微参考轨线y*(t)满足：

(a)得到的闭环系统所有解是全局有界的。

首先回顾GK类函数的定义。

定义1[21]如果函数递增且在原点右连续，且α(0)=0，则α属于K类函数。如果a=∞，且当时，则属于GK类函数。

为了解决输出跟踪问题，给出切换系统的增长无源概念。

定义2对于系统(1)的任意2个输入和，及对应的2个系统解和，2个输出和，如果存在光滑函数称为存储函数，GK类函数α和连续函数且使得：

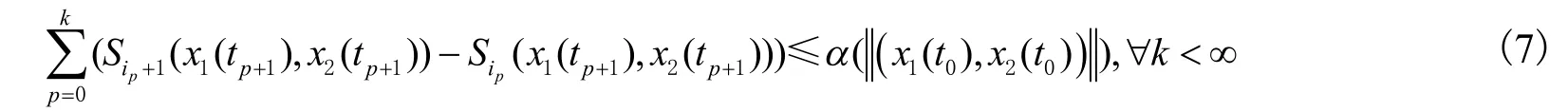
成立，那么称系统(1)在切换信号σ(t)下是增长无源的。

注1：不等式(6)意味激活子系统在激活时段具有增长无源性。在不等式(7)中，项是用来刻画在控制器ui作用下切换系统在有限时间段的能量变化程度。因为存储函数Si在切换时刻可以增加，定义2比文献[20]的增长无源定义更宽松，所适用的系统更广泛。当所有子系统有共同存储函数和共同的供给率，条件(7)自然成立。因此，这种增长无源性推广了经典增长无源性概念。

2 切换非线性系统的输出跟踪问题

本节主要是通过设计状态依赖型切换律和子系统的控制器使得切换非线性系统是增长无源的且输出跟踪问题可解。

首先，引入类似于径向无界的概念。

定义3[2]如果对于任何序列使得当是有界的且时，，则称是正则的。

下面利用切换非线性系统的增长无源理论解决输出跟踪问题。

定理1考虑系统(1)，对于任意如果存在非负光滑函数函数和光滑函数且和使得如下不等式成立：

设计切换律：

其中：

那么(a)系统(1)在切换律(12)是增长无源的。(b)如果对于t0≤t，是系统(1)在作用下的有界解且满足假设系统(1)的存储函数是正则的且则系统(1)在子系统控制器作用下输出跟踪控制问题是可解的，其中Ki是正定矩阵。

证明(a)作辅助系统：

因此，根据定义2，系统(1)在切换律(12)作用下是增长无源系统。

设计子系统控制器：

由式(16)和式(17)得到：

由式(19)得：

由式(20)得：

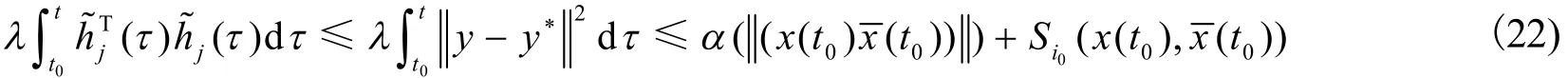
注2：式(8)和式(9)意味着在区域Ωi上增长无源不等式成立。对于任意i,j∈I如果每一个子系统是增长无源的。按照切换律(12)，存储函数在切换点处可能上升。因此，所设计的切换律比最小切换律更宽松。

3 级联切换非线性系统的输出跟踪

本节主要解决级联切换非线性系统的输出跟踪问题。考虑级联切换非线性系统。

其中(23a)和(23b)分别称为被驱动切换系统和驱动切换系统。对于系统状态是系统(23L)的切换信号。切换信号所产生的切换序列如下：

f0k(xa)是连续函数且。假设系统满足系统(1)在第二节的假设。系统(23)的状态。是系统(23)的切换信号，其中是第(k,i)子系统的输入。输出向量是连续函数且。复合切换信号产生的切换序列如下：

为了解决输出跟踪问题，做如下假设。

假设2存在正则且光滑的正定函数，连续函数光滑函数满足和的函数使得：

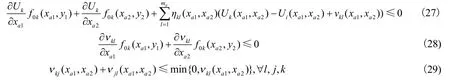
注3：定义

成立。而式(31)说明被驱动系统子系统的零动态是渐近稳定的。 因此，式(27)比式(31)弱。

定理2考虑(23)。对于如果(8)、(9)、(10)和(11)和假设2成立且那么

(a) 系统(23)是增长无源的。

(b) 如果对于t0≤t，是系统(23)的第个子系统在作用下有界解且那么系统(23)在控制器假设系统(23b)的存储函数是正则的且的作用下输出跟踪控制问题是可解的,其中Ki是正定矩阵。

证明(a) 定义

选择系统(23)的存储函数如下：

V(k,i)沿系统(23)求导得：

设计切换律如下：

根据切换律(36),得到切换序列(25)。式(10)和式(28)意味着分别在和递减。因为所以对于∀k∈N：

(b)类似于定理1的证明，输出跟踪问题是可解的。

注4：按照切换律(36)，被驱动系统和驱动系统可以异步切换。

4 仿真算例

本节将通过一个数值例子来验证所提出的理论方法。考虑如下系统：

图1 系统状态响应

图2 系统的输出

图4 切换系统能量的变化

图3 切换信号

5 结论

本文建立切换非线性系统增长无源理论并利用所建立的理论解决了切换非线性系统的输出跟踪问题。首先，在每个子系统输出跟踪问题都不可解的前提下，设计状态依赖型切换律解决输出跟踪问题。最后，设计复合切换律，解决级联切换非线性系统的输出跟踪问题，所设计的切换律允许驱动系统与被驱动系统不同步切换。

[1]Willems J C.Dissipative dynamical systems part I: General theory[J].Archive for Rational Mechanics and Analysis,1972,45(5):321-351.

[2]Desoer C A,Vidyasagar M.Feedback Systems:Input-output Properties[M].New York: Academic Press,1975.

[3]Fromion V,Scorletti G,Ferreres G.Nonlinear performance of a PI controlled Mi-ssile: An explanation[J].International Journal of Robust and Nonlinear Control,1999,9(8):485-518.

[4]Pavlov A,Marconi L.Incremental Passivity and Output Regulation[J].Systems and Control Letters,2008,57: 400-409.

[5]Bürger M,Persis C D.Dynamic coupling design for nonlinear output agreement and time-varying flow control[J].Automatica,2015,51: 210-222.

[6]Santoso H,Hioe D,Bao J,et al.Operability analysis of nonlinear processes based on incremental dissipativity[J].Journal of Process Control,2012,22(1): 156-166.

[7]Hines G H,Arcak M,Packard A K.Equilibrium-independent Passivity: A new definition and numerical certification[J].Automatica,2011,47(9): 1949-1956.

[8]Hamadeh A,Stan G B,Sepulchre R,et al.Global State Synchronization in Networks of Cyclic Feedback Systems[J].IEEE Transactions on Automatic Control,2012,57(2): 478-483.

[9]Hernandez-Gomez M,Ortega R,Lamnabhi-Lagarrigue F,et al.Adaptive PI Stabilization of Switched Power Converters[J].IEEE Transactions on Control Systems Technology,2010,18(3): 688-698.

[10]Sanders S R,Verghese G C.Lyapunov-based control for switched power converters[J].IEEE Transactions on Power Electronics,1990,7(1): 17-24.

[11]Weng Y,Gao X.Data-Driven Robust Output Tracking Control for Gas Collector Pressure System of Coke Ovens[J].IEEE Transactions on Industrial Electronics,2017,64(5): 4187-4198.

[12]Chakrabarty A,Buzzard G T,Zak S H.Output-Tracking Quantized Explicit Nonlinear Model Predictive Control Using Multi-Class Support Vector Machines[J].IEEE Transactions on Industrial Electronics,2017,64(5):4130-4138.

[13]Yang G,Yao J,Le G,et al.Asymptotic output tracking control of electro-hydraulic systems with unmatched disturbances[J].Iet Control Theory & Applications,2016,10(18): 2543-2551.

[14]Tse C K,Bernardo M D.Complex behavior in switching power converters[J].Proceedings of the IEEE,2002,90(5): 768-781.

[15]Lu B,Wu F,Kim S W.Switching LPV control of an F-16 aircraft via controller State reset[J].IEEE Transaction on Control systems Technology,2006,14(2): 267-277.

[16]Liberzon D.Switching in systems and control[M].Boston,MA: Birkhauser,2003.

[17]Jiang B,Shen Q K,Shi P.Neural-networked adaptive tracking control for switched nonlinear pure-feedback systems under arbitrary switching[J].Automatica,2015,61: 119-125.

[18]Li Q K,Zhao J,Dimirovski G M,et al.Tracking Control for Switched Linear Systems with Time-delay: A State-dependant Switching Method[J].Asian Journal of Control,2009,11(5): 517-526.

[19]Yang H,Cocquempo V,Jiang B.On stabilization of switched nonlinear systems with unstable modes[J].Systems & Control Letters,2014,58(10/11):703-708.

[20]Dong X X,Zhao J.Incremental passivity and output tracking of switched nonlinear systems[J].International Journal of Control,2012,85(10): 1477-1485.

[21]Zhao J,Hill D J.On stability,L2-gain andH∞control for switched systems[J].Automatica,2008,44(5): 1220-1232.

[22]Heemel W,WeilandS.Input-to-state stability and interconnections of discontinuous dynamical systems[J].Automatica, 2008,44:3079-3086.

Incremental Passivity-based Output Track for Switched Nonlinear Systems

PANG Hong-bo,LIU-Shuo
（College of Science,Liaoning University of Technology,Jinzhou 121001,China）

In this paper,the output track problem for a class of switched nonlinear systems is solved by using incremental passivity concept even if the output tracking problem for each subsystem is not solvable.First,the concept of incremental passivity for switched systems which allow the storage functions to increase at the switching time is proposed.Then,a state-dependent switching law is designed to render the switched system incrementally passive.Second,the output tracking problem is solved by using Lyapunov redesigning method.Moreover,a composite state-dependent switching law is designed to solve the output tracking problem for a class of cascaded switched nonlinear systems.Finally,a numeral example shows the effectiveness of the proposed method.

incremental passivity; switched nonlinear systems; output tracking; switching law

TP271

A

1674-3261(2017)05-0332-08

10.15916/j.issn1674-3261.2017.05.013

2017-04-23

国家自然科学基金项目(61703190)

庞洪博(1982-)，男，吉林公主岭人，讲师，博士。

责任编校：孙 林