基于热网络法的附件机匣热平衡研究

曾 红，崔学淼，魏 松，苏国营，王延忠

（1.辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001; 2.北京航空航天大学 机械工程与自动化学院 北京 100191）

基于热网络法的附件机匣热平衡研究

曾 红1，崔学淼1，魏 松1，苏国营2，王延忠2

（1.辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001; 2.北京航空航天大学 机械工程与自动化学院 北京 100191）

以附件机匣传动系统为研究对象，用热网络法建立了该传动系统的热平衡方程，并给出了热源、热阻和对流换热系数的计算模型；借助MATLAB编程进行计算，获得了附件机匣传动系统稳态温度场分布；搭建了温度测试实验台，对几个典型节点测温；结果表明：温度变化趋势一致性较好，但稳态温度值误差较大，对计算结果和实验结果对比，进行数据修正并通过实验验证，误差控制在 2%以内。因而，验证了采用热网络法计算附件机匣热平衡的可行性和修正系数选择的正确性。

附件机匣; 热网络法; 热阻; 热平衡; 修正

齿轮箱式附件传动系统常用于航空发动机，简称附件机匣，是飞机至关重要的传动部件[1-2]。在附件机匣内部，因为有多对高速齿轮啮合传动，所以其内部的温度场分布规律对整个发动机传动系统的稳定性、工作性能和抗胶合能力有重要影响[3]。所以，对附件机匣做热平衡分析十分必要。

热网络法是一种将热比拟电的分析策略，类比电学上的基尔霍夫电压和电流定律，将系统中各构件比拟为热源和热阻元件，将各个支路以及节点相连，建立航空发动机附件机匣的热平衡关系式，由热平衡关系式得到各节点的温度及变化率[4]，是一种适应性很强的热分析方法，在航天航空领域应用广泛。附件机匣热平衡问题不仅仅有热传导的现象，还有润滑油等介质参与，是一种复杂的传热系统。东北大学孙志礼教授采用有限元分析的方法，得到了航空发动机附件机匣壳体温度场分布以及附件机匣出油口处的润滑油温度[5]。史妍妍等基于Ansys软件进行仿真分析计算，得到了航空发动机附件机匣的稳态温度场分布[6]。附件机匣为满足动力传输的目的，其中有多对齿轮,采用Ansys建模比较复杂，而热网络技术，可以从整体上对附件机匣进行热平衡分析，在附件机匣关键位置上布置温度节点，通过对温度节点的求解，获得整个系统的热平衡状态。相对于有限元方法，热网络法操作简单、边界条件易于施加。

1 附件机匣热网络模型

对航空发动机附件机匣的热平衡系统进行一定程度的简化，将内部的齿轮、轴承和箱体等元素处理成节点如图1所示，图中各节点的含义见表1。

图1 附件机匣结构简图

表1 节点编号与对应位置区域

其中，A～I为轴系编号。假设齿轮表面的闪温不被计算在内，附件机匣即齿轮箱式附件传动系统内的温度差异就会很小，在这种情况下，附件机匣温差的非稳态传热流程就能够忽略不计，那么附件机匣内的温度分布就可以选择用平均温度来取代[7]。

因附件机匣系统庞大以及设置点较多，仅列出部分系统热网络图。在图2绘制的热网络模型里，用Qij来代表齿轮接触啮合的产热热源，用Qia以及Qib来代表轴承摩擦运动的产热热源，用Ricj来代表节点i、节点 j两者间存在的导热热阻，用RiVM来代表节点i、节点M两者间的对流换热热阻，其中，i以及j为节点标号。

2 功率损失及热传递计算模型

2.1 功率损失计算模型

2.1.1 齿轮副

近年来，很多专家对齿轮啮合功率损失的计算进行了研究。安德森和勒文塔尔法是一种被普遍采用来计算齿轮啮合功率损失的有效算法，这种方法在保证准确的同时十分简洁[8]。

图2 系统部分热网络图

在安德森和勒文塔尔法的计算过程中中，相啮合齿轮的总功率损失为：

式中: 用qs来表示齿轮齿面平均滑动功率损失，用qr来表示齿轮齿面滚动功率损失，用qw1和qw2来表示齿轮风阻损失，用qGi来表示旋转轴外径与润滑油之间的搅油功率损失、盘光面与润滑油之间的搅油功率损失和齿轮与润滑油之间的搅油功率损失，具体计算方法见文献[9]。

2.1.2 滚动轴承

在工作过程中，附件机匣轴承全部的产热如下：

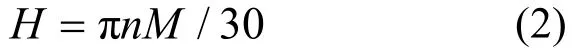
其中，用H来表示附件机匣轴承在工作过程中所产生的全部发热量，单位为W；用M来表示相关部件的总摩擦力矩，单位为N·m；用n来表示附件机匣轴承的内圈运转速度，单位为r/min。式中，总摩擦力矩的计算公式为：

其中，用Ml来表示载荷摩擦力矩，单位为N·m，用Mv来表示粘性摩擦力矩，单位为N·m，用Ma来表示圆柱滚子轴承附加摩擦力矩，单位为N·m。

2.2 传热系数的公式推导

2.2.1 热传导系数

在推导过程中，假定物体平壁的长度数值以及宽度数值与其厚度数值相比大得多，用λ来表示导热系数，单位为W/(m·k)；用L来表示热量在顺着热流方向上的传导长度，单位为m；用S来表示导热的面积，那么物体的导热热阻有如下公式：

在推导过程中，用λ来表示导热系数；用L来表示与热流传导方向呈90°的轴向长度；用a和b来分别表示圆柱的内壁及外壁的直径，单位为m；那么薄圆环的导热热阻可以用如下公式表示：

则圆柱体导热热阻为：

2.2.2 对流换热系数

对流有两种情况，一种是平面对流，另一种是圆柱面对流，在推导过程中，平面和位于平面间的润滑介质的对流换热系数用α来表示；用S来表示平面上与热流流动呈90°方向上的面积，那么平面对流系数可以用如下公式表示：

则圆柱对流系数计算公式为：

其中，α表示齿轮箱式附件传动系统的齿轮与润滑油相互的强迫对流换热系数，可以用如下公式表示：

附件机匣即齿轮箱式附件传动系统轴承与润滑油相互的强迫对流换热系数为：

式中: 用Re来表示雷诺数；用PY来表示润滑油本身的普朗特数；用ko来表示润滑油本身的导热系数，单位为W/(m·k)；用L来表示对应的定型尺寸，单位为m，本文中L为齿轮分度圆直径。

3 热平衡方程组的建立及求解

从热平衡基本原理中可以得出，在传动系统经过一段时间发展最终行成稳定状态时，对于任意一个节点，任一瞬间其流入与流出的热流量一致，因此航空发动机附件机匣传动系统的热网络平衡方程可以用如下公式表示：

其中，Ti、Tk和Tj为节点温度，Rki和Rij为节点热阻。

图2所示的热网络模型，其系统部分热平衡方程组如下：

已知附件机匣外界的温度TA=150 ℃，附件机匣内部的油雾温度TM=170 ℃，将各个热阻导入，通过MATLAB编程来解方程[9]，得出各个节点在航空发动机附件机匣热平衡状态下的温度，见表2。

表2 各节点温度

附件机匣生热绝大部分为齿轮和轴承工作时产生的摩擦热，其传递给齿轮、旋转轴、箱体，同时各部件和润滑油及油雾进行强制对流换热，故齿轮啮合面、齿轮与轴接触面、轴的上下端以及轴承外圈与箱体接触面为主要热源。由于节点较多，难以对每个节点进行测温实验，故选择节点 1、节点11、节点12、节点32、节点48作为典型节点。

图3为以上所选典型节点的温度在时间的变化下产生的响应曲线。

图3 几个典型节点的温升曲线

由表2可见，附件机匣传动系统最大的温度处在传动功率大、转速相对不高的轴上；同样温度最高的轴承也出现在传动功率大、转速相对不高的轴的两端，具体呈现外圈温度低，内圈温度高的特点；由于外壳的表面积较大，同时外壳与外界环境存在对流换热，因而其温度较低。由图3所示的节点1、11、12、32、48温度随时间的响应曲线，可以观察得到它们的温度变化过程，温度最终趋于平衡，达到各自的稳定值。

4 实验验证

为了检验上述所建立热网络模型的准确性和精度，本研究搭建了节点1、11、12、32、48的温度测试试验台，其中，节点1的温度测试系统如图4(a)所示，主要由红外测温仪、齿轮箱和计算机组成[10]，测温现场如图 4(b)所示，整个测温实验台工作在真实的工况下，具体参数见表 3，计算机采集数据如图5、图6、图7所示。

图4 齿面温度测试原理图

表3 齿轮传动工况

图5 节点1的温度计算值与测量值对比曲线

图6 节点11和节点32的温度计算值与测量值对比曲线

图7 节点12和节点48的温度计算值与测量值对比曲线

如图5、图6、图7所示，随着转速的增加，不同测点的温度以不同的趋势增加，运行约30 min后，温度趋于平衡，达到各自的稳定值，各节点计算值与测量值曲线一致性良好。以上5个节点温度的理论值与测量值比较见表4。

从表4可以看出：几个节点温度的试验值与理论计算值的误差在12% ～ 15%左右。分析原因有如下两点：

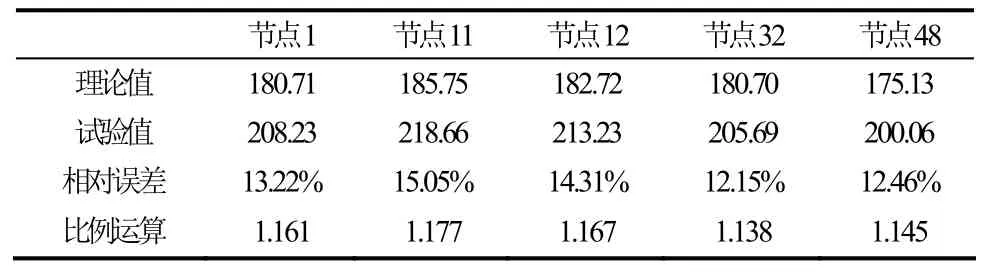
表4 几个典型节点计算值与试验值比较

（1）建立热网络模型时，由于简化，导致热网络模型有一定误差。使计算值产生误差。

（2）附件机匣内的齿轮功率损失，轴承发热量、传热系数等都是利用经验公式计算，有一定的误差，对稳定值计算结果有较大影响。

5 结果修正

在分析了实验数据的误差以及产生误差的影响因素后，发现误差较大，有必要对理论计算结果进行修正，经计算值和测量值对比计算，引入修正系数。具体修正系数确定方法为：首先，对稳态各点对应的计算值和测量值进行比例运算，见表 4；然后，将所得比值进行统计学分析，求取其期望值作为修正系数。经计算，期望值为1.16。最后，修正系数和计算值进行乘法运算，从而完成稳态计算值的修正，见表5。

表5 几个典型节点修正值与试验值比较

从表5可以看出，修正值和测试值基本接近，误差在 2%以内，说明修正系数选择正确，修正方法可行。

6 结论

（1）利用热网络法对航空发动机齿轮箱式附件传动系统的热平衡问题进行了研究，建立了包含75个节点的热网络模型，并对功率损失和热传递计算模型进行了分析研究；

（2）从计算结果发现该系统最大的温度处在传动功率大、转速相对不高的轴上；而轴承呈现外圈温度低，内圈温度高的特征。由此可见，采用热网络法分析符合热力学定律，说明了热网络法的有效性；

（3）通过对几个典型节点进行温度测试，测量值的曲线走势与计算值的曲线走势一致性良好，曲线基本吻合。稳定值数据误差在12% ～ 15%左右，分析了误差产生的原因并提出了修正系数的确定方法；

（4）对计算值进行修正之后，数据误差降到2%以内，从而验证了热网络法分析附件机匣传动系统的可行性和修正系数选择的正确性，为复杂机构传动系统尤其是航空发动机附件机匣热平衡问题的研究提供了一种便捷有效的分析手段。

[1]《航空发动机设计手册》总编委会.航空发动机设计手册[M].北京: 航空工业出版社,2002.

[2]Russom,Dennis M.Investigating and resolving accessory gearbox failures on allision 501-K series engines[J].American Society of Mechanical Engineers,1998,22(4):281-287.

[3]孙志礼,闫明,李国权.竖壁对流换热系数计算模型的探讨[J].东北大学学报: 自然科学版,2005,26(5):484-487.

[4]屈金祥.航天器系统热分析综述[J].红外,2004(10):20-27.

[5]孙志礼,闫明,杨强,等.附件机匣出油口润滑油温度计算方法[J].东北大学学报: 自然科学版,2006,27(6):685-688.

[6]史妍妍,孙志礼,李国权,等.附件机匣稳态热分析方法研究[J].机械设计,2009,26(6): 22-25.

[7]吴晓铃,陈立锋,秦大同,等.土压平衡盾构机行星减速器热平衡分析[J].中国机械工程,2012,23(7):777-782.

[8]周廷美,何庆,周浩,等.基于热网络法的汽车变速器热平衡分析[J].机械传动,2014,38(3): 143-146.

[9]马从谦,沈允文,陈国定.渐开线行星齿轮传动设计[M].北京: 机械工业出版社,1987: 89-91.

[10]刘昌华,骆广进,何卫,等.基于热网络的某主轴系统稳态热分析[J].中国机械工程,2010,21(6): 631-635.

[11]陈星.基于红外热像的喷油润滑齿面温度测量技术研究[D].长沙: 中南大学,2013.

Heat Balance Study of the Accessory Gearbox Based on Thermal Network Method

ZENG Hong1,CUI Xue-miao1,WEI Song1,SU Guo-ying2,WANG Yan-zhong2
（1.College of Mechanical Engineering and Automation，Liaoning University of Technology，Jinzhou 121001,China ;2.College of Mechanical Engineering and Automation，Beijing University of Aeronautics and Astronautics，Beijing 100191,China）

The accessory gearbox drive system as the object of study,the transmission of the heat balance equations based on the thermal network method is established,and the calculation models of heat source,thermal resistance and convective heat transfer coefficient are given.The temperature field distribution of accessory gearbox is obtained through the calculation of heat balance equations by MATLAB program.The temperature test bench is set up and the temperature of several typical nodes in transmission is tested.The results show that the thermal network method results are in good agreement with experimental data but the steady-state temperature error is severe.By comparing the calculation results with the experimental results,data are corrected and verified by experiments,the errors are controlled within 2%.Therefore,The feasibility of using heat network method to calculate the heat balance of the accessory case and the correctness of the correction coefficient’s selection are verified.

accessory gearbox; thermal network method; heat resistance; heat balance;correction

V233.1

A

1674-3261(2017)05-0302-05

10.15916/j.issn1674-3261.2017.05.006

2017-06-13

国家自然科学基金资助（51275020）

曾红(1964-)，女，辽宁朝阳人，教授，硕士。

http:// http://kns.cnki.net/kcms/detail/21.1567.T.20170904.1610.002.html

责任编校：刘亚兵