无量纲指标趋势分析法在风电机组齿轮箱故障预警诊断中的应用

顾煜炯，贾子文，尹传涛，任玉亭

(1. 华北电力大学 新能源电力系统国家重点实验室，北京 102206；2. 国华能源投资有限公司，北京 100007)

无量纲指标趋势分析法在风电机组齿轮箱故障预警诊断中的应用

顾煜炯1，贾子文1，尹传涛1，任玉亭2

(1. 华北电力大学 新能源电力系统国家重点实验室，北京 102206；2. 国华能源投资有限公司，北京 100007)

针对风电机组运行工况复杂多变，早期故障特征提取十分困难的问题，提出无量纲指标趋势分析法以实现风电机组齿轮箱故障的早期诊断。通过阶比重采样方法对齿轮箱振动信号进行预处理，将非平稳时域信号转化成平稳角域信号，引用无量纲因子指标反映机组早期故障程度变化趋势；利用指标趋势分析法建立风电齿轮箱故障预警模型，并通过实验室数据和现场数据进行分析验证。结果表明，该方法能够比较准确的对风电机组齿轮箱早期故障进行诊断，并能初步估测故障发生时间，达到故障预警目的。

风电齿轮箱；阶比重采样；无量纲指标；趋势分析法；早期故障诊断

由于风电机组受风速、风向影响，长期在变转速、变负荷状态下运行，使得机组运行工况具有波动性、间歇性的特点。齿轮箱作为变速机构，因其结构设计紧凑，部件之间耦合性较强，长期受到交变载荷和冲击载荷作用，容易造成齿轮磨损、点蚀和轴承表面损伤等故障，齿轮箱故障在风电机组机械类故障中所占比例较高[1]。目前，国内外学者对齿轮箱故障做了大量研究：罗毅等[2]运用小波包和倒频谱分析方法实现了对风电机组齿轮箱在复杂环境中运行状态退化的监测；罗荣等[3]通过对冗余小波包的改进有效提取出齿轮箱强噪声中的微弱信号，提高了对齿轮箱故障诊断的灵敏度；林近山等[4]通过多重分析趋势波动分析法，对齿轮箱相近故障模式清晰分离，准确分析出齿轮箱故障；陈法法等[5]运用局部切空间排列与支持向量机的方法实现了对齿轮箱故障高精度、自动智能化的诊断；Wilkinson等[6]利用机组SCADA数据对数据预测、自组织映射和物理建模三种方法进行横向比较，并通过实际数据验证三种方法对机组异常检测的有效性。

目前，变工况设备运行状态监测与故障诊断大多通过数据挖掘手段，对已发故障信号进行量化处理，以实现对设备故障模式的识别工作[7]，但对故障早期诊断问题的研究较少。本文通过对风电机组齿轮箱振动数据的无量纲指标趋势分析，实现对机组齿轮箱故障早期故障诊断的工作。

1 基于角域信号无量纲因子趋势的故障特征提取

风电机组运行工况的波动性使得现场采集的振动信号具有明显非线性、非平稳性特征[8-10]。运用传统方法对振动时域信号进行分析处理，很难提取出明显、有效的故障特征，尤其在机组发生故障初期，故障信号特征微弱，传统分析方法对风电机组早期故障诊断变得十分困难。

为解决以上问题，文章提出阶比重采样方法[11]对风电机组齿轮箱振动信号进行预处理，将非平稳的时域信号转化成平稳的角域信号，之后对角域信号进行无量纲指标分析计算，提取信号特征，作为后续机组齿轮箱早期故障诊断的基础。

1.1阶比重采样

旋转机械的振动同转速联系紧密，例如，风机齿轮箱非恒定转速会造成振动信号出现非线性特征，传统的故障特征提取方法难以从振动信号中解析出有效信息，无法准确分析设备运行情况。阶比重采样方法只需保证旋转机构每一转采样点数一致，即等角度采样原则，实现振动和转角信号的同步采样，再通过数值差值运算，实现非平稳等时间间隔时域信号向平稳等角度间隔角域信号的转换。为避免传统硬件价格昂贵、安装受到现场限制等问题，文章采用软件方式实现此过程(见图1)。

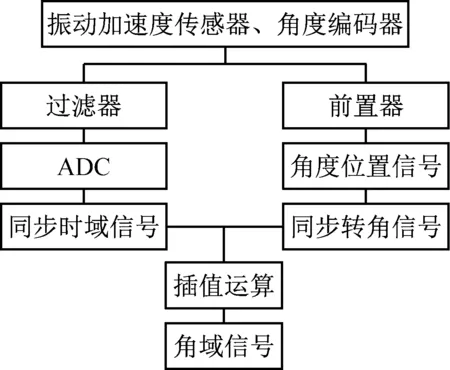
图1 阶比重采样流程图Fig.1 Order resampling flow chart

假设等时间间隔采样下的时域振动信号为{x1,x2,…,xi,…,xn}，每个振动信号对应时刻的集合为{t1,t2,…,ti,…,tn}，角度编码器对应时刻转轴的角度位置集合为{θ1,θ2,…,θi,…,θn}。

(1) 假设编码器记录的相邻两个角度之间转轴的运动过程为匀加速运动，将振动数据集合同角度集合一一对应，即时间量替换成角度量，完成时域振动信号向角域信号的转化。

(2) 考虑到整个过程机组转速非恒定的情况，上述生成的角域信号并非严格意义上的等角度形式。找出转轴位置集合中角度变化最小的相邻两点，即转轴转速最低的时刻，结合振动信号采样频率，计算出等角度采样频率k。根据采样定理，k值大于最大阶比的2倍，这里取6～10倍。得出整个采集时间段重构的角度序列{θ1,θ2,…,θi,…,θm}，其中m≥n。通过线性差值，找到重构角域序列在原始角域序列中的位置，计算出差值点位置对应的设备振动加速度值，最终得出等角度间隔角域信号。

1.2机组齿轮箱早期故障特征提取

齿轮箱故障发生初期，信号变化微弱，故障特征很难提取。传统的量纲指标虽能够对机组早期故障进行诊断分析，如方差指标，峰峰值等，其计算数值极易受到设备运行工况干扰，影响早期故障诊断结果的准确性[12-13]。本文引入新的无量纲指标[14-16]：奇异谱熵Hs、功率谱熵HF、相似性因子Ff和跳跃性因子Jf。这些因子与被监测设备运行工况无关，但对设备早期故障变化敏感，因子值随故障程度发展具有较为明显的单调趋势变化[17-18]。所以，文章以角域序列无量纲指标随时间的趋势变化作为风电机组齿轮箱早期故障诊断的特征。各个无量纲因子内容如下：

(1) 奇异谱熵Hs，应用相空间重构方法，将离散角域信号序列X=[x1,x2,…,xn]嵌入到长度为K的空间中，形成N行K列的轨迹矩阵A，并对其进行奇异值分解得[δ1,δ2,…,δk]，构成原始角域信号的奇异值谱。定义原始信号的奇异值谱熵为

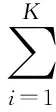
(1)

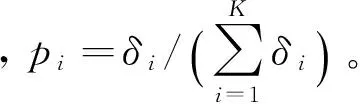
(2) 功率谱熵HF，设X(ω)为离散角域信号序列X经过傅里叶变换后的阶比序列，其功率谱为

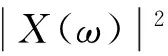
(2)

信号由角域到阶比的转换过程中遵循能量守恒定律，即信号总能量为各个频率分量对应能量之和。所以，阶比信号的功率谱熵表示为

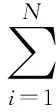
(3)

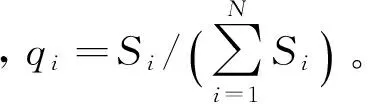
(3) 相似性因子Ff，相似性因子采用盒维数的分析方法实现对数据微弱变化的甄别工作。首先要针对盒维数的计算规则对时域信号进行标准化处理

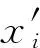
(4)

式中：xγ(ti)为ti时刻幅值；|xγ(j)max|为记录数据中幅值绝对值最大值；K为放大因子，通常为整数。

盒维数计算要对信号波形进行单元格划分，基于分形原理：要保证整个信号波形与单元格内波形具有较强的相似性。设F是s实数集合Rn中任意非空有限子集，记N(F,φ)为最大边长φ能覆盖F集合的最小数字，则F的盒维数计算公式为

(5)

式中，ln()为以e为底的对数，相似性因子为

Fλ=dimBF

(6)

(4) 跳跃性因子Jf，此因子主要反映振动波形的幅度调制，通过式(4)对原始角域信号标准化处理，计算其方差值

(7)

这些无量纲因子能够定性分析与故障有关的波形形状信息，较好地反映变负荷大型旋转设备的故障发生趋势。但是由于旋转设备结构组成及故障模式的不同，这些无量纲因子对故障的敏感程度也不尽相同，只有将多种无量纲因子结合起来，综合分析各因子趋势发展规律，才能更准确有效地实现对设备早期故障的诊断工作。

1.3案例分析

以张北某风电场某品牌1.5 MW风电机组为例，通过2013年5月的二年检记录发现齿轮箱一级行星轮系太阳轮严重磨损，该处测点振动数据由3月中旬开始出现异常变化。截取该测点3月份31天历史数据进行研究，每天截取60 s数据作为样本。

以第一天的60 s数据为例进行阶比重采样，如图2所示，对应频域图和阶比图如图3所示。

通过观察图3可以发现，角域信号阶比谱图中各个阶比成分要比时域信号频域图中各个频率成分表现更为清晰。说明经过阶比重采样处理后的数据能够更为明显、集中的体现设备运行特征。

分析2013年整个3月份共31天的历史数据，每天提取60 s振动数据进行趋势指标计算，结果如图4所示。

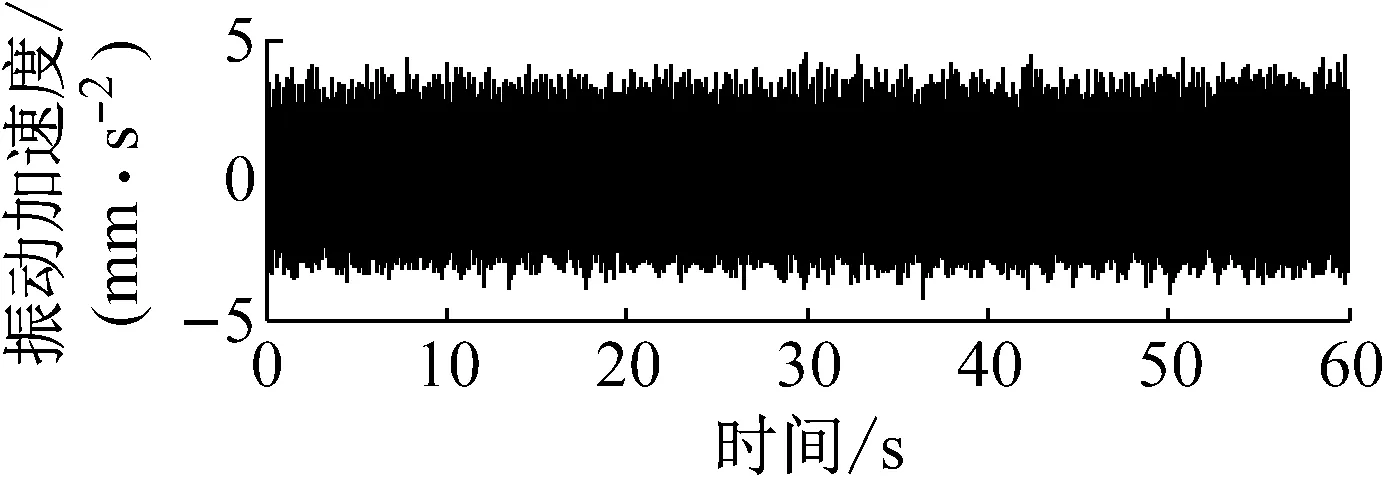
(a) 时域信号

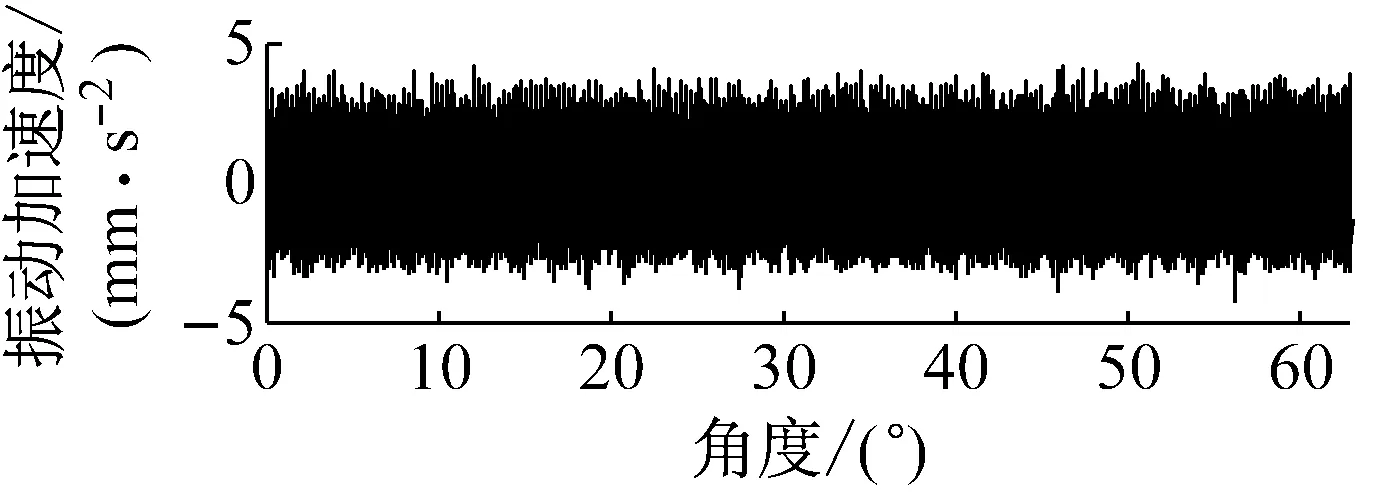
(b) 角域信号图2 行星齿轮箱时域信号与角域信号Fig.2 Time-domain signal and angle-domain signal of planetary gearboxes

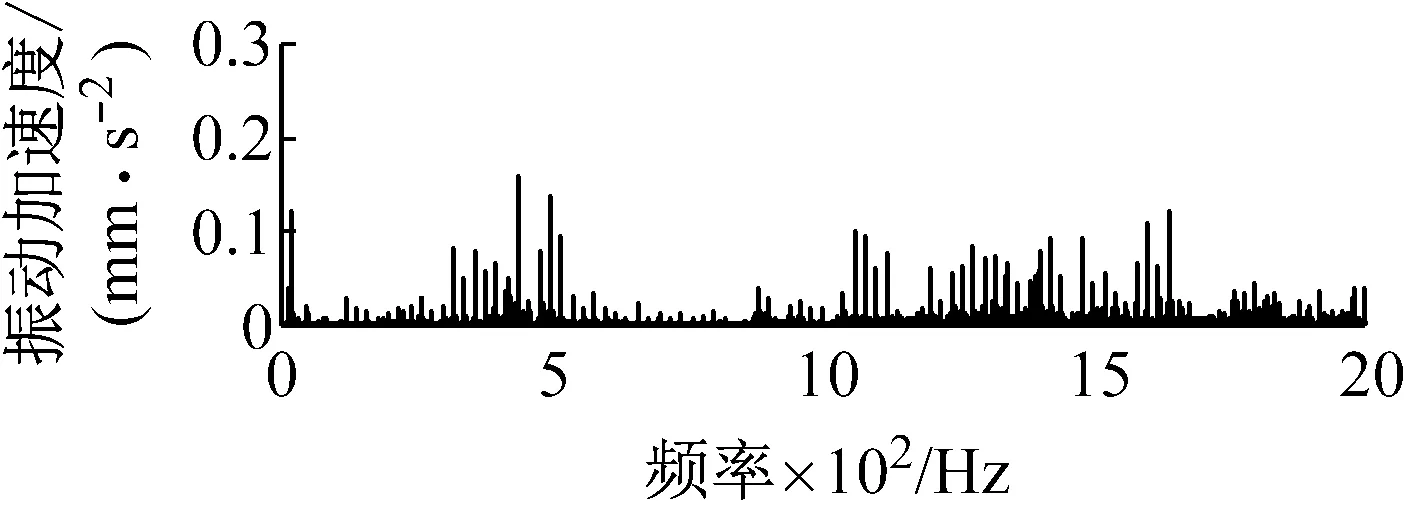
(a) 频谱图

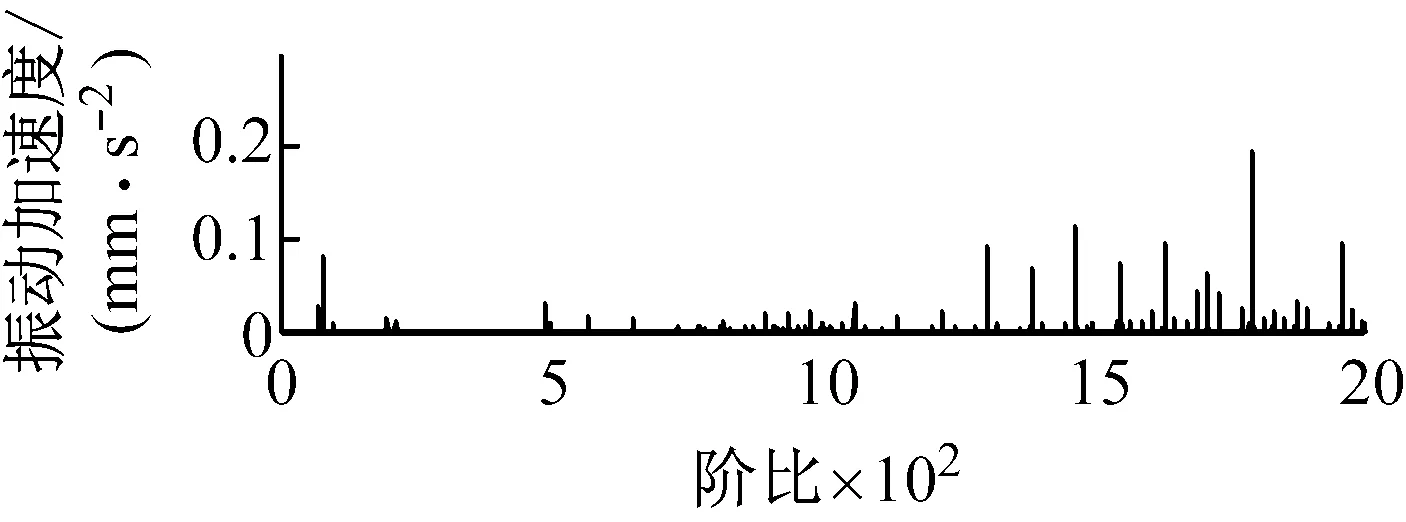
(b) 阶比谱图图3 行星齿轮箱的频域谱和阶比谱Fig.3 Frequency spectrum and order spectrum of planetary gearboxes

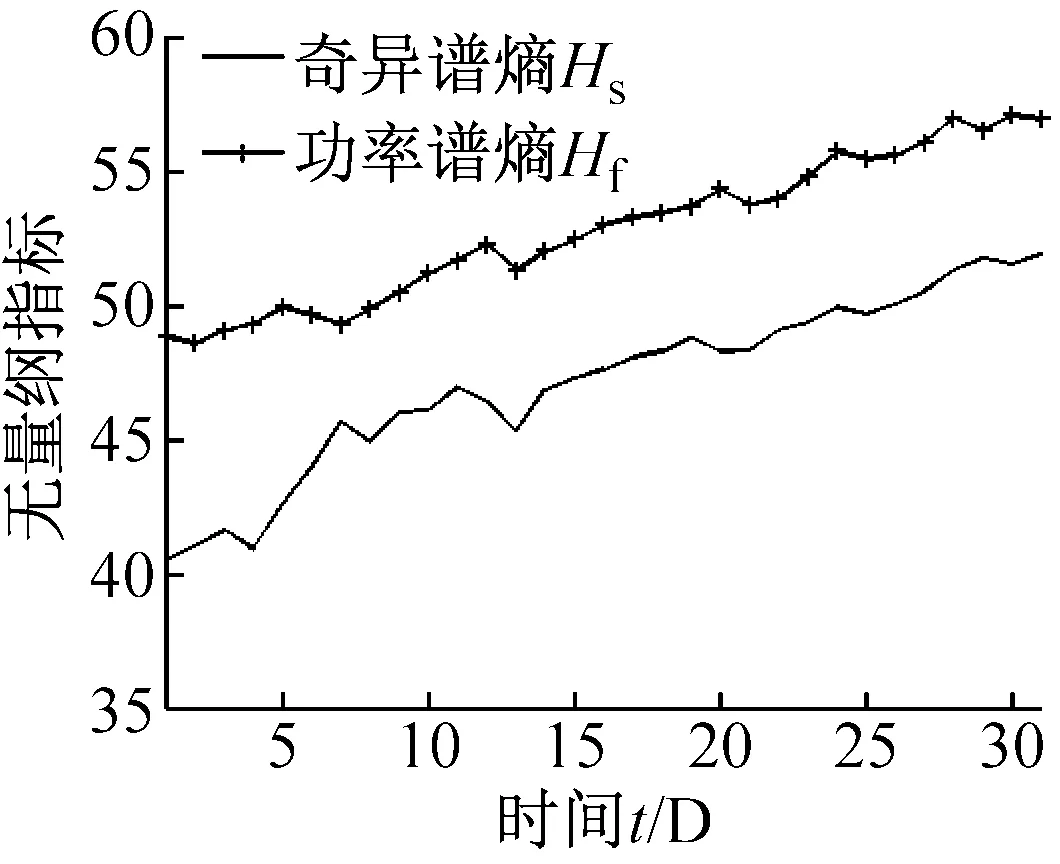
(a)

(b)

(c)图4 故障无量纲指标、有量纲指标趋势变化图Fig.4 The trend of fault non-dimensional parameters and dimensional parameters

对各图4中指标趋势观察发现，奇异谱熵、功率谱熵等无量纲指标与峰峰值、方差值等有量纲指标相比，前者对风电机组齿轮箱的早期故障在数值趋势变化上更敏感。

提取该机组同一测点1月份31天的正常数据，进行无量纲因子值计算，如图5所示。

观察图5中各因子趋势可以发现：无量纲因子在设备正常状态下，各个因子值的变化不大；有量纲因子，如方差值仍有较大波动，说明无量纲因子的变化机组客观运行状况影响较小。

通过对图4、图5两图对应因子趋势的观察，可以看出：无量纲因子在机组出现故障时，其趋势较正常状态有较为明显的单调性变化；而传统的有量纲因子在数值上虽有一定差异，但是整个监测过程数值波动较大，数据趋势体现不明显。所以可以通过对机组角域数据无量纲指标的趋势作为研究对象进行分析，完成齿轮箱故障的早期诊断工作。

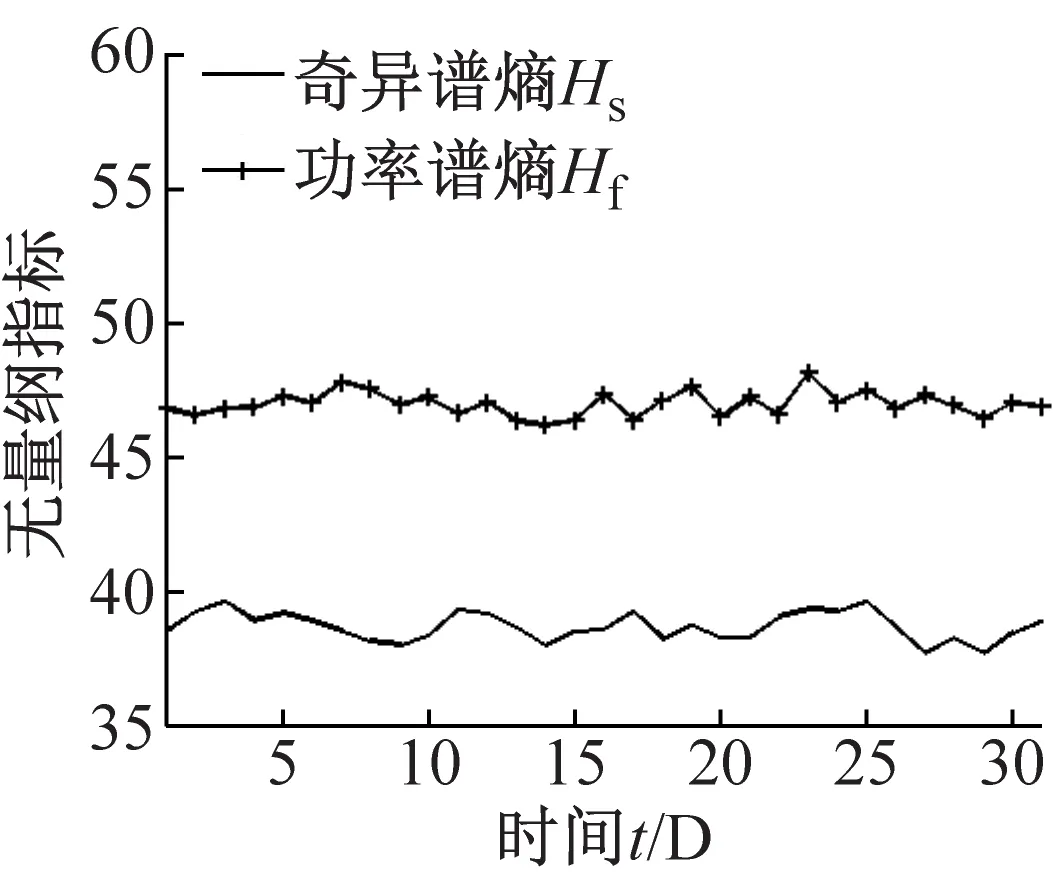
(a)

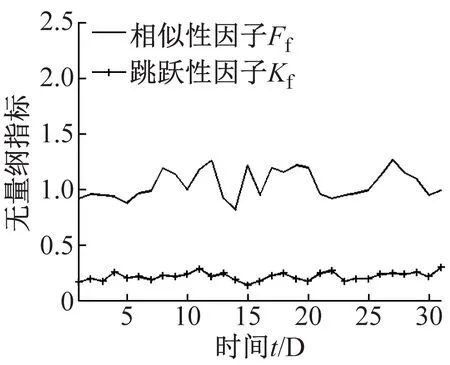
(b)

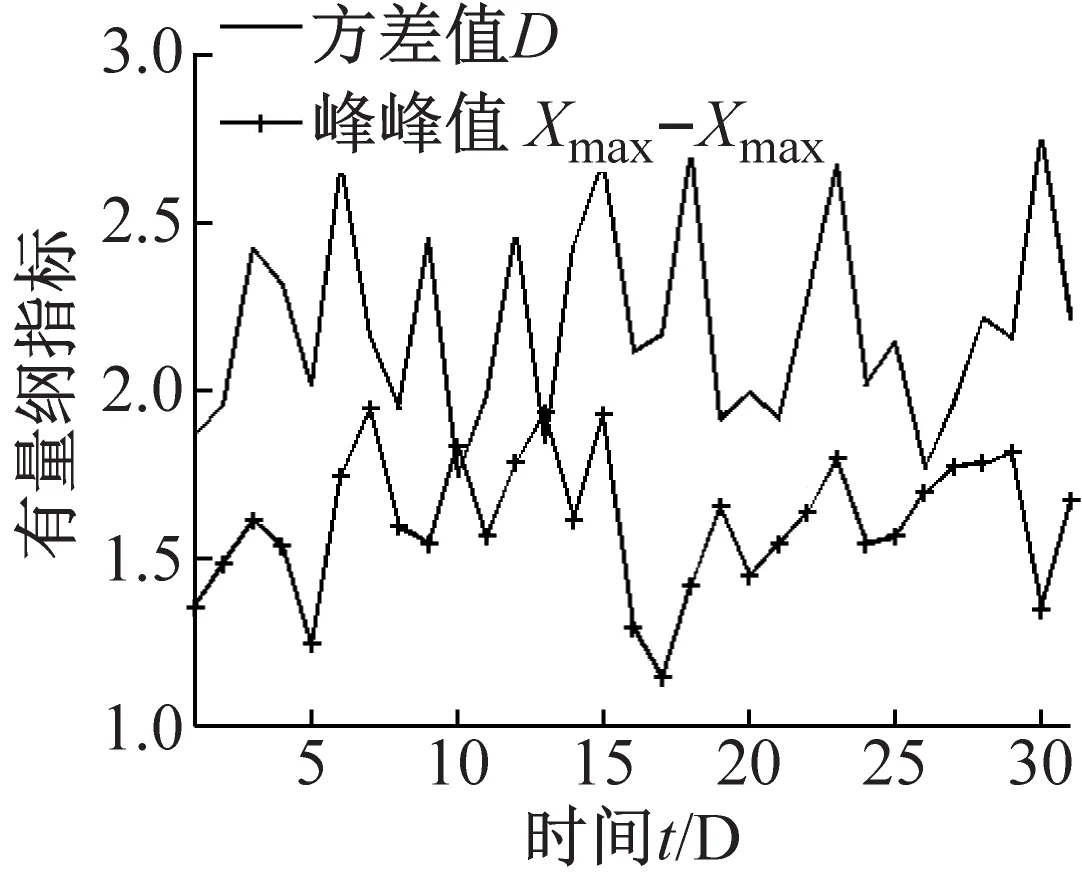
(c)图5 正常无量纲指标、有量纲指标趋势变化图Fig.5 The trend of normal non-dimensional parameters and dimensional parameters

2 无量纲指标趋势分析

利用无量纲指标对早期故障信号变化敏感的特点，通过对风电机组齿轮箱振动监测数据向角域数据的转化，计算无量纲指标幅域参数，提取趋势图谱特征，根据机组不同故障模式下各个指标参数随时间趋势变化的差异性，实现对风电机组齿轮箱故障的早期诊断工作。具体过程如下所述：

(1) 获取被监测设备振动数据，经过阶比重采样方法处理，生成角域信号并进行无量纲指标计算，得出各个无量纲值在当前工况下随时间的趋势变化。

(2) 考虑到无量纲趋势曲线会出现波动现象，为提高指标趋势辨识度，文章采用“单位圆”方法对无量纲趋势曲线进行处理。

设趋势曲线上的点为X=[x1,x2,…,xn]，将曲线每相邻三个点为一组，表达式如下

Z=Zkk=1,2,3,…,n-2

(8)

式中，Zk=[xk,xk+1,xk+2]，过Zk中三个点可以确定一个圆，过Zk中的点xk+1做该圆的切线L，如图6所示，其中B点表示xk+1。

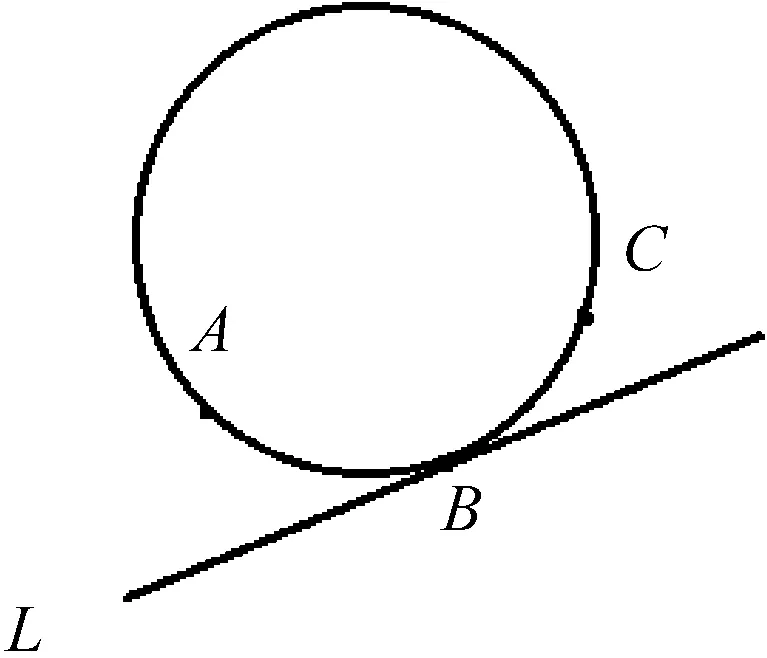
图6 单位圆切线示意图Fig.6 The of Unit circle tangent

按要求计算所有确定单位元切线L的斜率，其数列为s=[s1,s2,…,sn-2]，绘出时间-斜率曲线，即t-s曲线。

(3) 通过观察各无量纲指标t-s曲线中的斜率值，可判断出各因子值单调性随时间的变化。所以，借鉴模式识别中的链码技术，采用三邻域方向：0表示斜率值为负值；1表示斜率值为0；2表示斜率值为正值。其中斜率值表示单位圆切线L的斜率。通过对各无量指标进行固定顺序排列，设备在不同的工况下，会出现一组“代码”与之对应，作为故障征兆，实现对设备的故障模式诊断工作。编码表达式如下

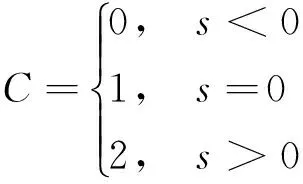
(9)

式中：C为编码值；s为无量纲因子值单位元切线斜率。

(4) 通过单位圆方法确定出t-s曲线观察可发现：各无量纲指标斜率随时间均会在某个数值上下波动，虽然能通过各无量纲指标曲线的单调性确定机组故障模式，但指标斜率的不稳定性造成故障发生时间难以确定。所以文章利用相关系数概念，结合滑动窗口方法确定设备早期故障诊断时间。

设滑动窗口[td,tu]，td为时间下限，tu为时间上限，则窗口内斜率与时间的相关系数表达式为

(10)

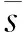
因为|R|≤1，|R|值越接近1，s与t两者相关性越强。为在t-s图中找到相对水平的曲线区间，即无量纲指标趋势变化稳定，要求|R|的值尽可能的接近0(因为理论上水平直线表明两变量之间无线性关系)。当然，为保证机组故障模式诊断的客观性与准确性，还要做出以下几点限定：

(1) 为保证相关系数结果的客观性，滑动窗口内包含点数要大于2个，同时保证最终分析结果的可参考性，滑动窗口内的点数应至少大于等于5个；

(2) 为保证s与t的高度不相关性，取|R|≤0.2；

(3) 在确定多个无量纲指标t-s窗口区间时，要保证各指标时间估计的区间有交集出现，这样才能准确说明故障发生的时间。

3 风电机组齿轮箱故障预警实验分析

文章所用实验数据来自NREL(National Renewable Energy Laboratory)实验平台提供的风电机组监测数据。通过应用无量纲指标趋势分析方法对平台齿轮箱已知故障进行计算，得出对应故障模式征兆，作为故障早期诊断标准。因为各个无量纲指标针对不同故障模式的敏感程度略有差异，所以，为保证最终分析结果的准确性，在文中在已经提出的无量纲指标的基础上，增加重复性因子Rf和波形裕度Cl，共同作为风电机组齿轮箱的故障征兆，实现齿轮箱早期故障的诊断工作。其中重复性因子Rf对波形的重复性进行定量分析，因子值随故障发展的波形重复性差变而发生变化；波形裕度Cl对振动信号形状和趋势的细微波动变化比较显著，大量实验证明这两个因子可以作为判断旋转机械早期故障的指标。机组齿轮箱为一级行星轮系两级平行轮结构，其结构图如图7所示。

该齿轮箱各部件主要参数如表1所示。

其中，已知齿轮箱存在低速级太阳轮轻微局部故障以及低速轴大齿轮轻微分布式故障，在齿轮箱行星轮级和低速轴部分的箱体表面安装振动加速度传感器，高速轴末端安装角度编码器，用来测量高速轴转速，采样频率均为40 000 Hz，实现对故障部位的数据采集。通过保证实验平台足够长的运行时间，使齿轮箱存在轻微故障的部件劣化程度加深，实现对齿轮箱故障由轻微到严重的发展过程。文中实验平台由调速电机带动主轴旋转，通过程序控制电机转速，保证在0.5 h内实现齿轮箱高速轴由1 200 r/min匀变速到1 800 r/min，之后连续运行4 h。整个过程重复30次，即实验平台运行总时间为135 h。下面分别对齿轮箱存在的两种故障应用无量纲指标趋势分析方法进行早期诊断。

针对太阳轮局部故障，首先截取齿轮箱升速时第一个60 s的行星轮级振动数据，对其进行阶比重采样，通过对振动数据预处理，消除振动信号由于变化转速带来的非线性等不良影响，提高后续指标提取与趋势分析的准确性。

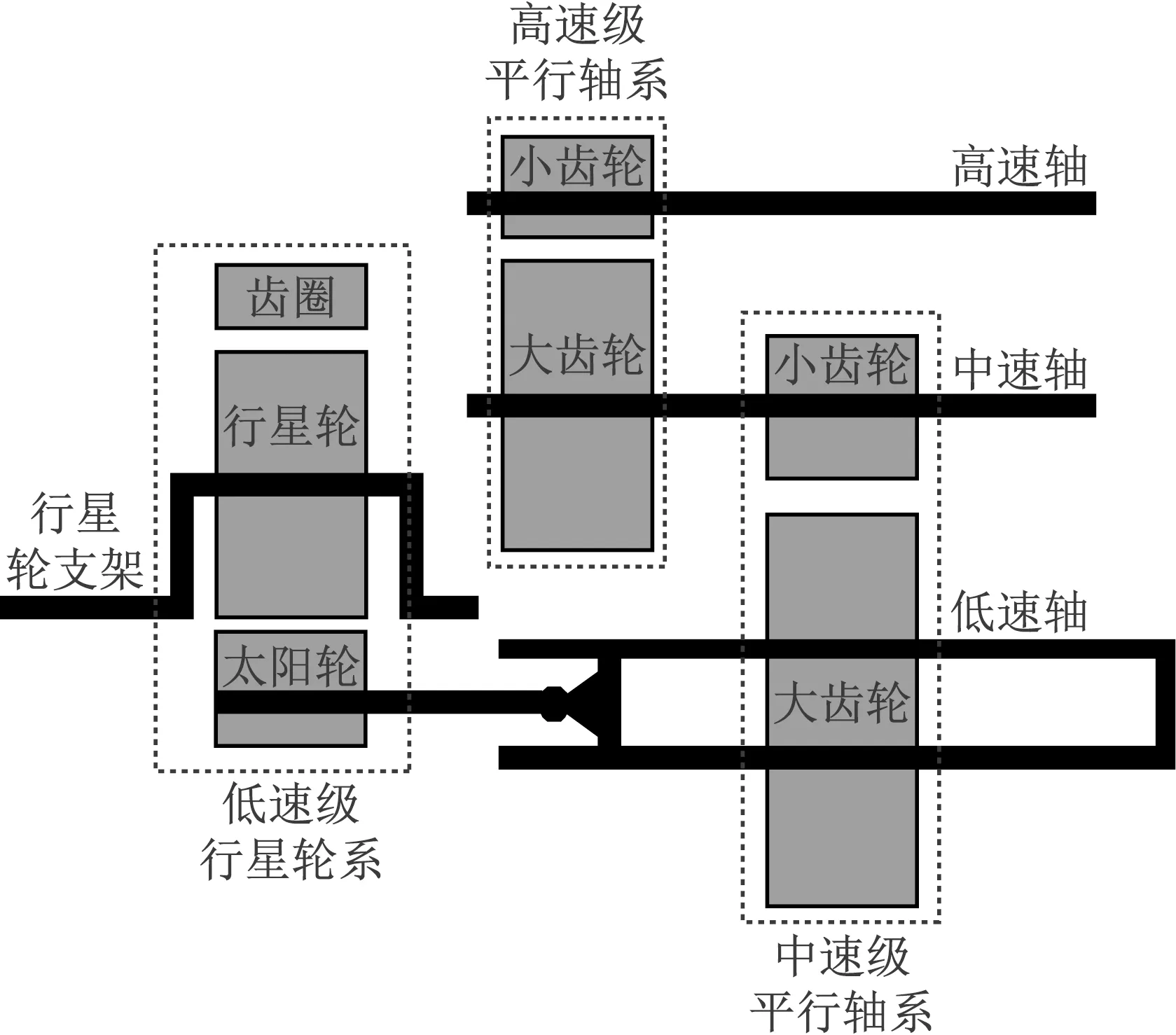
图7 行星齿轮箱结构简图Fig.7 Structure diagram of planetary gearboxes

表1 齿轮箱结构参数Tab.1 Gear element dimensions and detial

运用无量纲指标趋势分析方法，对30次启停试验升速过程的首个60 s的振动信号进行预处理，之后进行无量纲指标分析计算，得出各无量纲指标的t-s曲线以及特征数据如图8、表2所示。

应用链码编辑技术中的三领域方法，对单调增(即表中“+”)的指标趋势赋值为2，单调减的(即表中“-”)赋值为0，形成对应故障模式的一组编码。同时，还需求出各无量纲指标符合要求区间的交集，作为判断故障发生时间的依据，具体结果如表3所示。

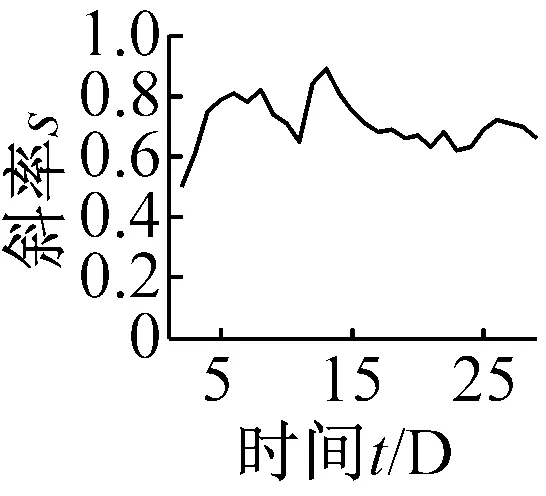
(a) 奇异谱熵Hs

(b) 功率谱熵Hf

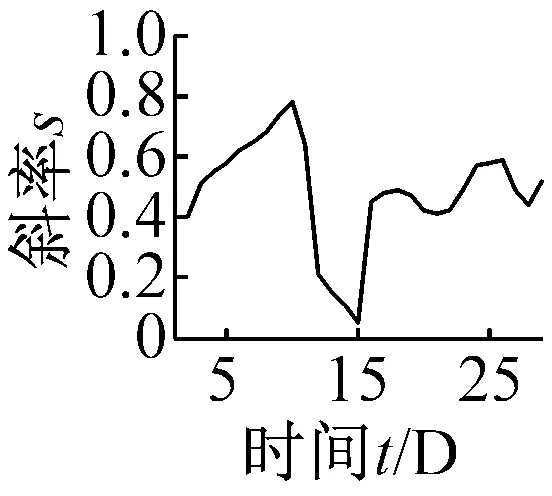
(c) 相似性因子Ff

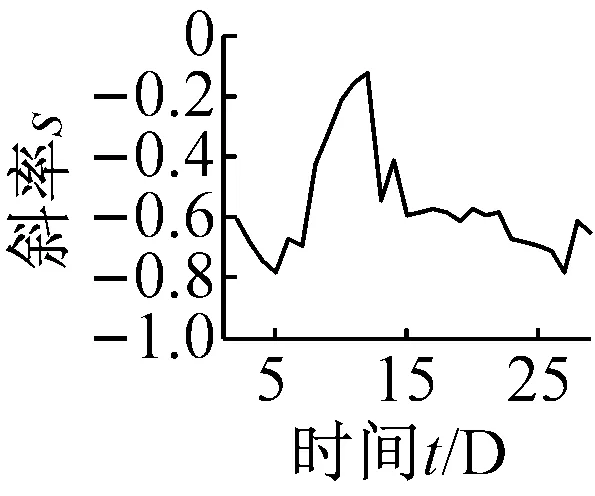
(d) 跳跃性因子Jf

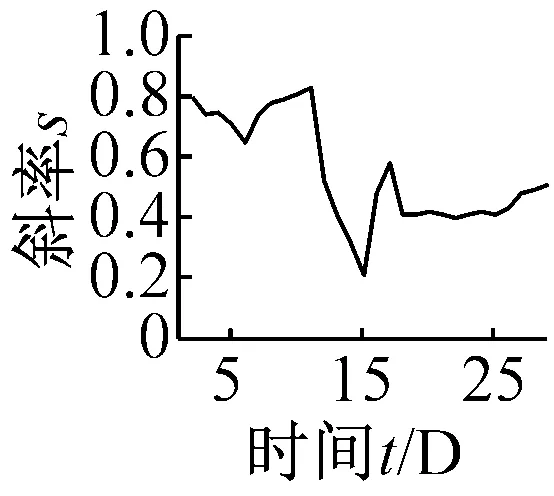
(e) 重复性因子Rf

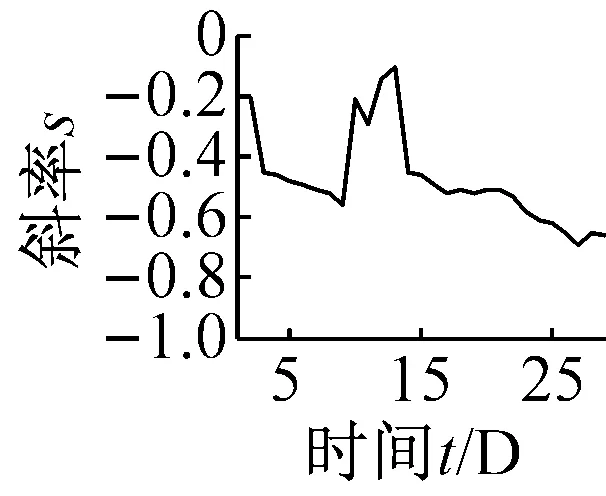
(f) 波形裕度Cl图8 无量纲指标时间-斜率图Fig.8 The t-s figures non-dimensional parameters trend

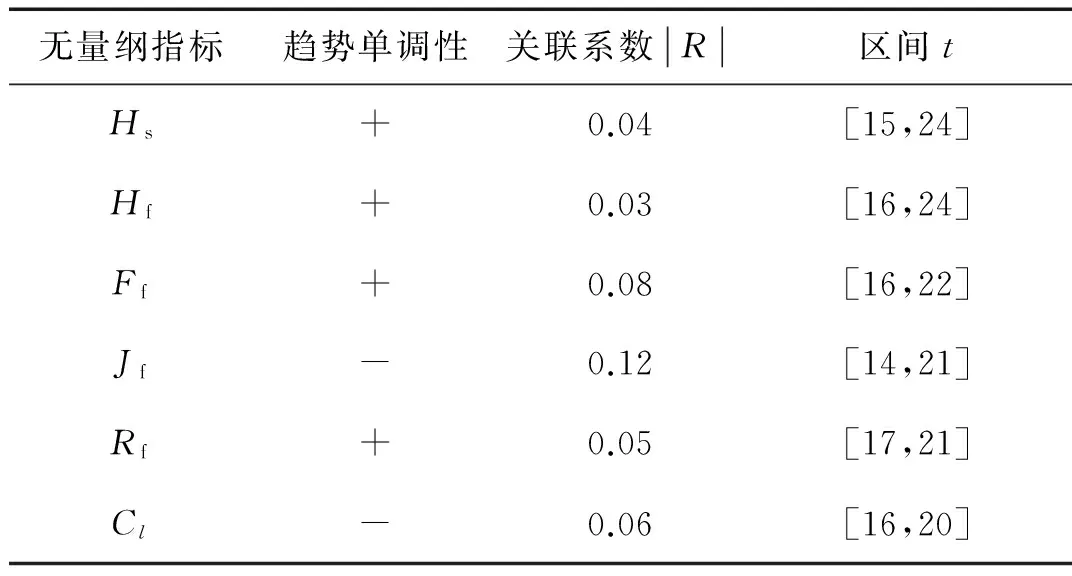
表2 无量纲指标趋势分析表Tab.2 The trend analysis of non-dimensional parameters

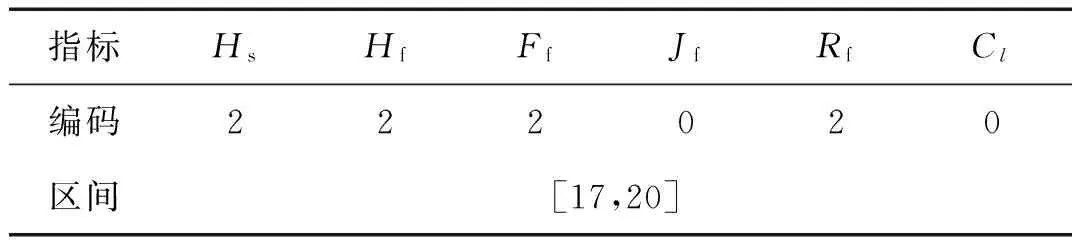
表3 太阳轮局部故障信息表Tab.3 The details of localized sun gear fault

由表3的结果可知：齿轮箱早期太阳轮局部故障发生时，其故障特征编码为“222020”，故障发生时间在试验台运行的第17天左右。

用同样的方法，对试验台早期低速轴大齿轮分布故障进行分析诊断，得出各无量纲指标的t-s曲线以及特征数据如图9、表4所示。

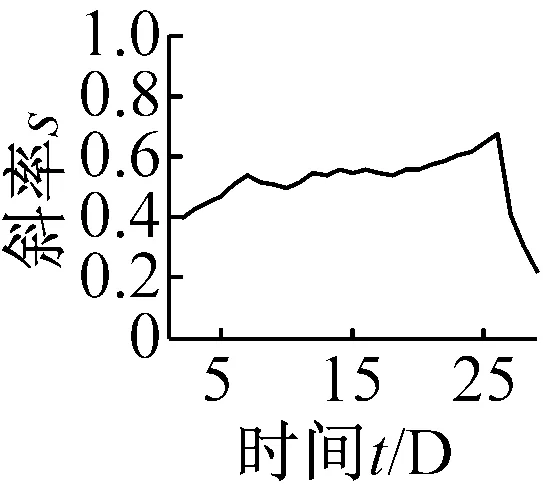
(a) 奇异谱熵Hs

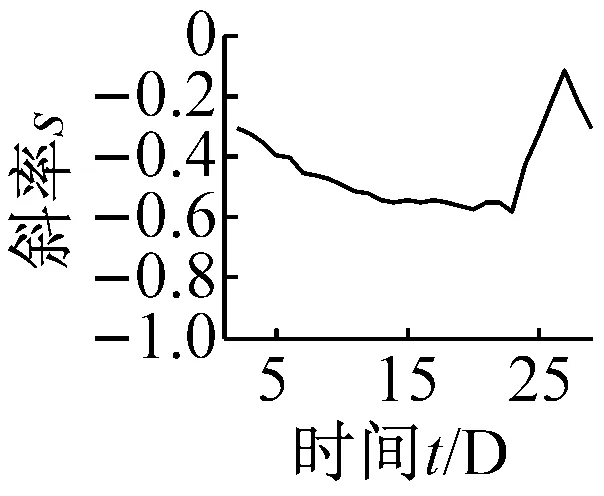
(b) 功率谱熵Hf

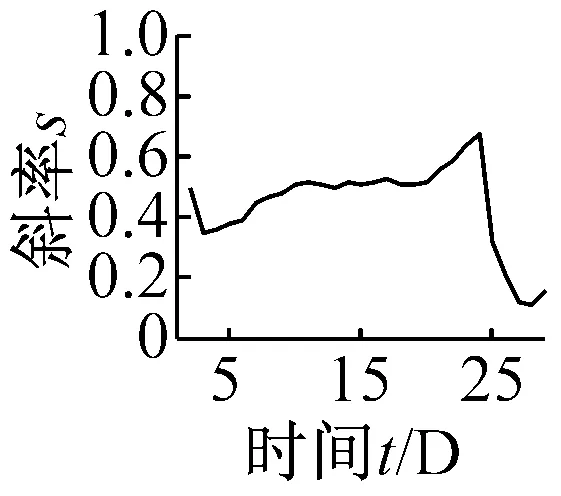
(c) 相似性因子Ff

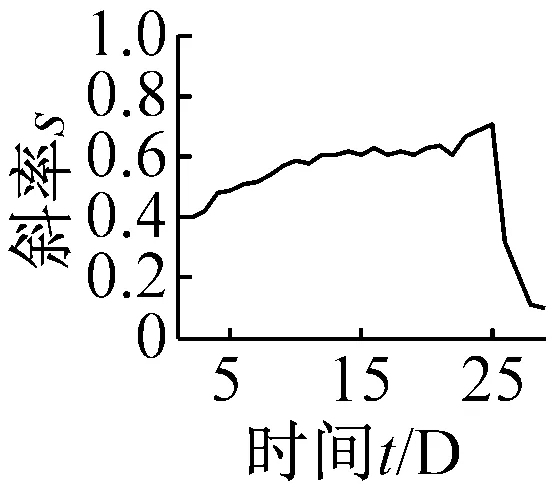
(d) 跳跃性因子Jf

(e) 重复性因子Rf

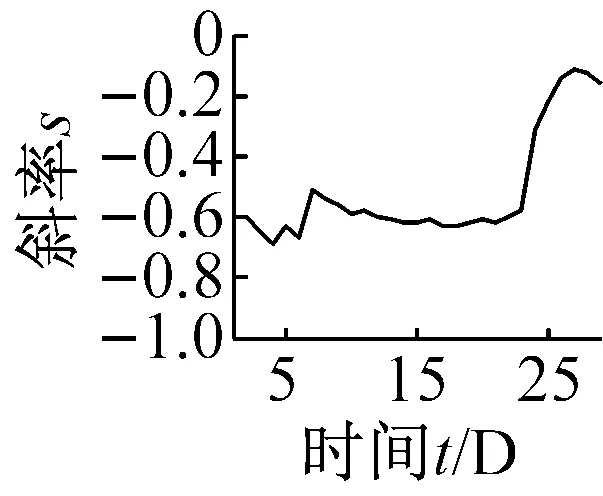
(f) 波形裕度Cl图9 无量纲指标时间-斜率图Fig.9 The t-s figures non-dimensional parameters trend

表4 无量纲指标趋势分析表Tab.4 The trend analysis of non-dimensional parameters

对表4内容进行编码及区间合并，得出表5内容。

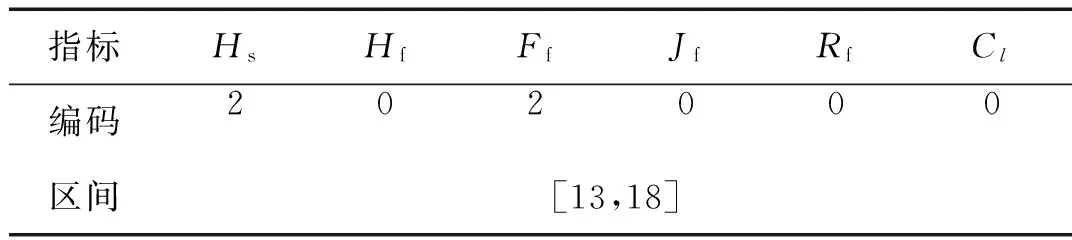
表5 大齿轮分布故障信息表Tab.5 The details of distributed bull gear fault

同样，通过表5可知：齿轮箱早期大齿轮分布故障的故障特征编码为“202000”，故障发生时间为试验台运行的第13天左右。

通过实验数据分析：每个故障模式根据其无量纲因子趋势变化的不同，结合链码编辑方法，会有唯一的编码与之相对应，同时根据符合趋势要求的区间分析，可以得出估算出故障发生的时间。

因为各个无量纲因子值趋势会因设备结构和故障模式的不同发生变化，这样会直接影响各因子单位元切线斜率s数值分布，导致不同结构特征的设备之间故障模式编码结果以及故障发生时间会有一定差异。所以，为保证此分析方法的可靠性，在进行设备故障模式编码过程中，尽量保证仿真环节中的实验设备结构和故障模式特征数据与实际中的设备相一致。

4 实例分析

以河北沧州某风电场2期3号1.5 WM双馈风电机组为例，其齿轮箱结构为一级行星轮系两级平行轮系。此机组在2014年6月发生低速级大齿轮磨损故障，选取2014年4月份30天的数据为研究对象，对齿轮箱低速级振动测点数据进行分析研究。取4月份每天60 s的振动数据，进行无量纲指标的趋势分析。其中，各个指标的t-s曲线如图10所示。

对各无量纲因子趋势图进行数据分析，结果如表6所示。

对各无量纲指标趋势进行编码和区间整合工作，结果如表7所示。

通过与实验环节得出的标准样本进行对比，最终得出诊断结果，沧州某风场2期3号机组于2014年4月中旬出现齿轮箱低速轴大齿轮分布式故障。应用此方法分析与现场得到的结果相一致，并且更早时候诊断出机组故障。同时，通过各指标斜率值与标准数据对比也可发现，实测数据指标的斜率值要略小于实验阶段的值，说明实际风机故障的发展速度较实验室设备的故障要缓慢。这是因为在实际中，风电机组受风资源影响，机组不是时刻满负荷运行。而实验室设备受人为控制，在相同的时间内，要比现场风机的有效工作时间要长，故障发展的速度更快。

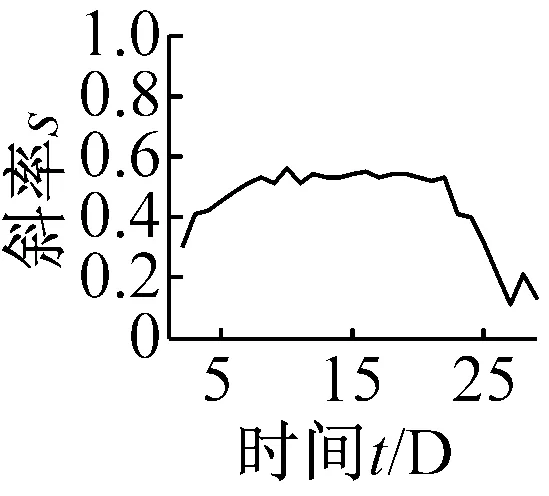
(a) 奇异谱熵Hs

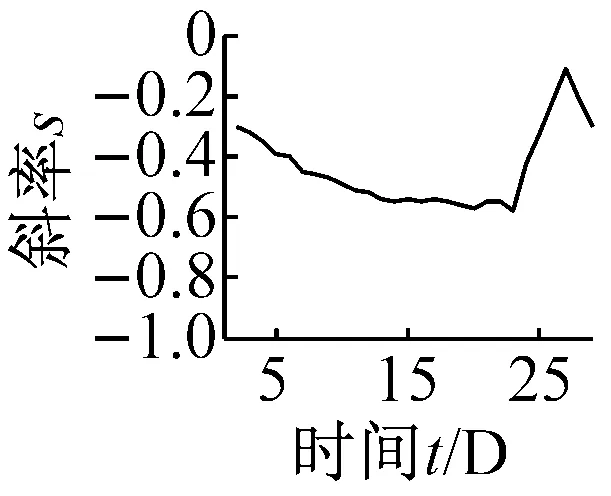
(b) 功率谱熵Hf

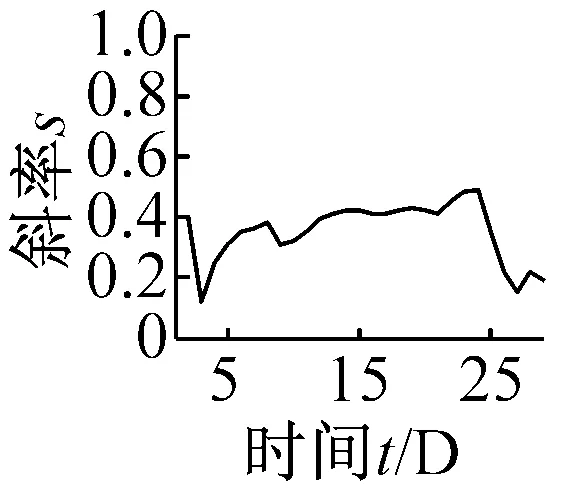
(c) 相似性因子Ff

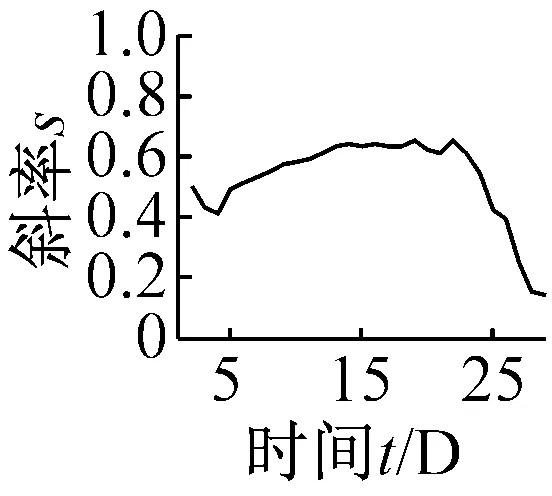
(d) 跳跃性因子Jf

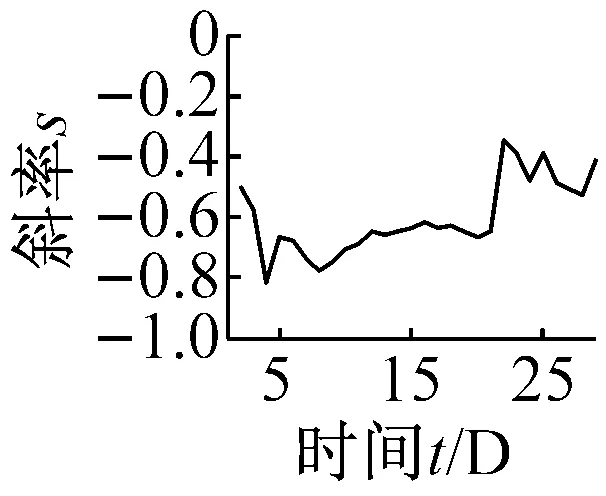
(e) 重复性因子Rf

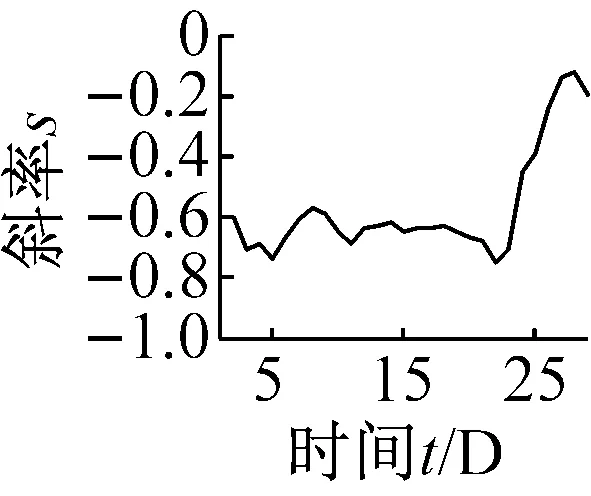
(f) 波形裕度Cl图10 无量纲指标时间-斜率图Fig.10 The t-s figures non-dimensional parameters trend

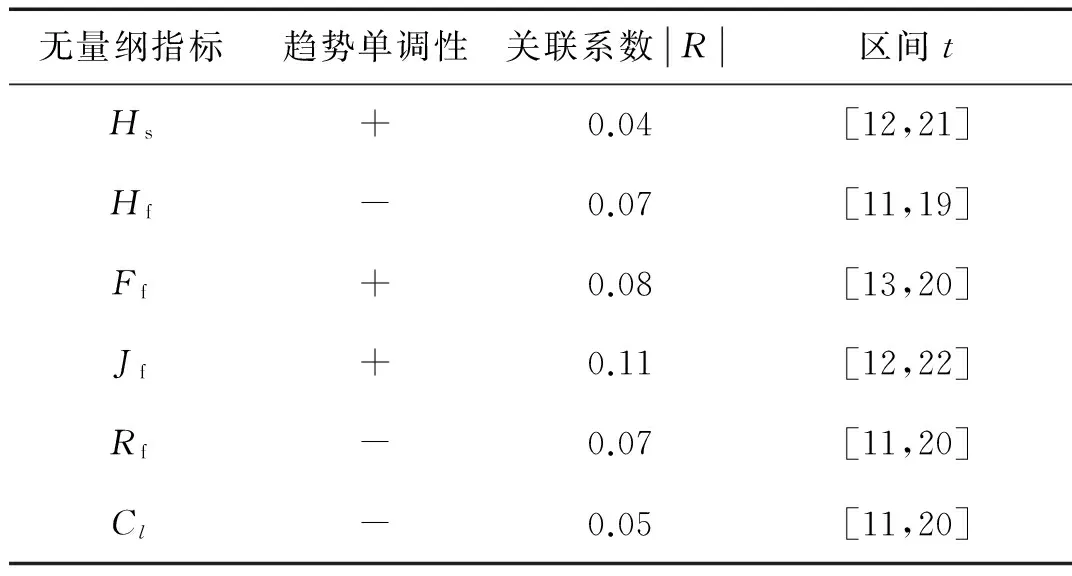
表6 无量纲指标趋势分析表Tab.6 The trend analysis of non-dimensional parameters

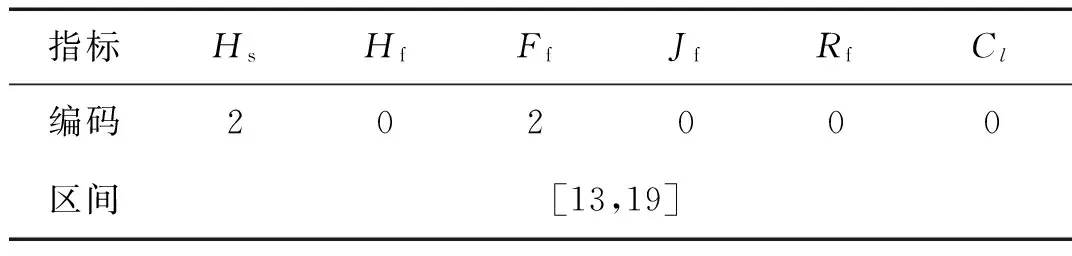
表7 实测信号信息表Tab.7 The details of actual signal

运用多元离群检测方法对同一机组故障进行分析。其中采用马氏(Mahalanobis)距离对离群点的距离进行求解，各个无量纲因子值作为分析参数。截取机组同年2月份齿轮箱低速级正常振动数据进行训练，得出正常工况下标准样本：

{Hs,Hf,Ff,Jf,Rf,Cl}={47.21,37.79,13.25,6.45,0.119,4.896}

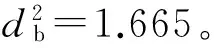
将风场2014年4月份30天的无量纲因子值与标准样本进行马氏距离边界计算，结果如表8所示。

观察表8可以发现，马氏距离值在第21天超出故障距离边界值，说明基于马氏距离的多元离群检测方法在第21天发现机组出现故障，而文章提出的分析方法在第13天诊断出机组故障。说明无量纲指标趋势分析方法能够更早的发现机组齿轮箱出现的故障。

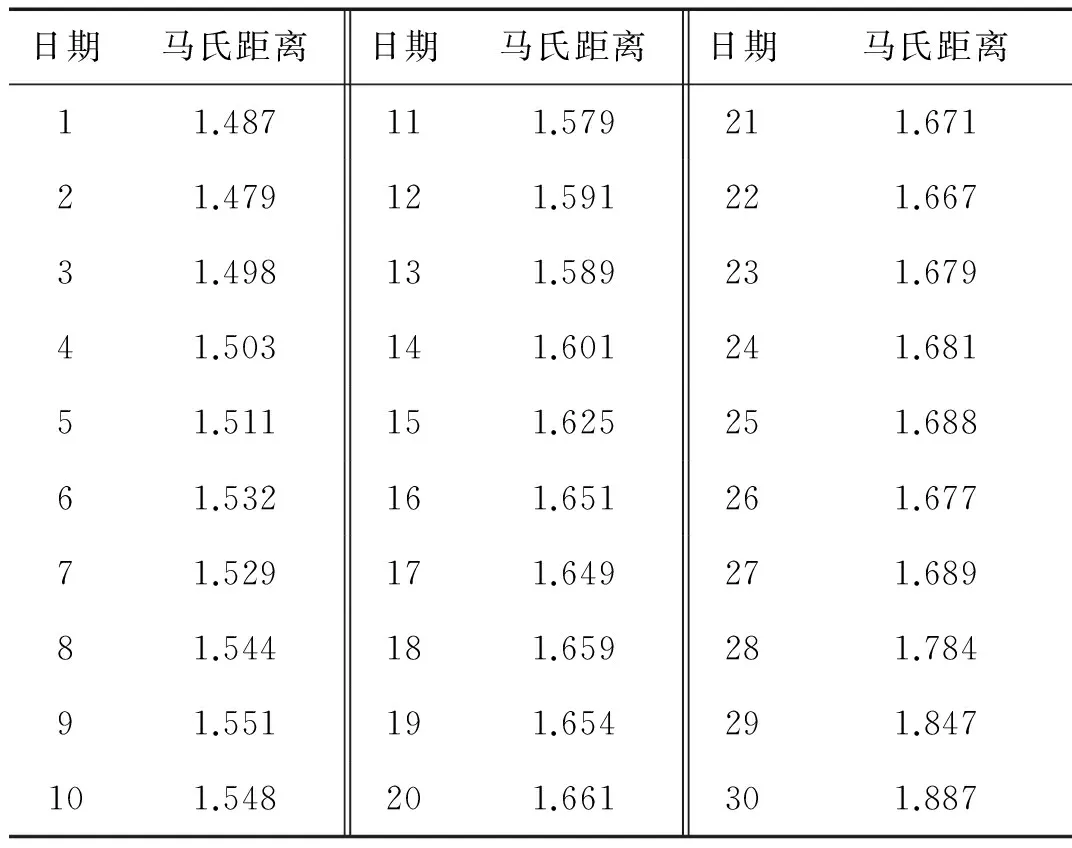
表8 马氏距离表Tab.8 The distance of Mahalanobis

5 结 论

(1) 运用阶比重采样技术，实现了风电机组振动数据由波动向平稳的转化过程，通过时域数据向角域数据的转变，明确故障数据信息，提高后续诊断结果的准确性。

(2) 引入无量纲指标的概念，运用其对设备早期故障振动信号变化敏感的特点，对不同故障模式下的多个指标趋势进行分析，将各指标趋势变化特性作为设备工况特征，克服了传统方法对在期故障特征提取困难的问题；

(3) 运用单位元方法实现对无量纲指标趋势图的处理，并运用链码编辑方法，以简洁直观的方式实现对机组齿轮箱故障模式的诊断；同时通过滑动窗口与关联系数相结合的分析方法，实现对风电机组齿轮箱故障发生时间的估计工作。

[1] 帅军庆.电力企业资产全寿命周期管理理论、方法及应用[M].北京：中国电力出版社，2010:95-97.

[2] 罗毅，甄立敬.基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J].振动与冲击，2015,34(3):210-214.

LUO Yi, ZHEN Lijing. Diagnosis method of turbine gearbox gearcrack based on wavelet packet and cepstrum analysis[J]. Journal of Vibration and Shock, 2015,34(3):210-214.

[3] 罗荣，田福庆，冯昌林，等.冗余小波包改进及其在齿轮箱故障诊断中应用[J].机械工程学报，2014,50(15):82-88.

LUO Rong, TIAN Fuqing, FENG Changlin, et al. Improved redundant wavelet packet decomposition and its application in gearbox fault diagnosis[J]. Journal of Mechanical Engineering, 2014,50(15):82-88.

[4] 林近山，陈前.基于多重分析去趋势波动分析的齿轮箱故障特征提取方法[J].振动与冲击，2013,32(2):97-101.

LIN Jinshan, CHEN Qian. Fault feature extraction of gearboxes based on multifractal detrended fluctuation analysis[J]. Journal of Vibration and Shock, 2013,32(2):97-101.

[5] 陈法法，汤宝平，苏祖强.基于局部切空间排列与MSVM的齿轮箱故障诊断[J].振动与冲击，2013,32(5):38-47.

CHEN Fafa, TANG Baoping, SU Zuqiang. Gearbox fault diagnosis based on local target space alignment and multi-kernel support vector machine[J]. Journal of Vibration and Shock, 2013,32(5):38-47.

[6] WILKINSON M, DARNELL B, VAN DELFT T, et al. Comparison of methods for wind turbine condition monitoring with SCADA data[J]. IET Renewable Power Generation, 2014,8(4):390-397.

[7] 曹斌.风电机组振动监测与故障诊断系统研究[D].广州：广东工业大学，2014.

[8] 郭建英，孙永全，王铭义，等.基于计算机仿真的风电机组系统可靠性综合[J].机械工程学报，2012,48(2):2-8.

GUO Jianying, SUN Yongquan, WANG Mingyi, et al. System reliability synthesis of wind turbine baesd on computer simulation[J]. Journal of Mechanical Engineering, 2012,48(2):2-8.

[9] 董肖峰，练继建，杨敏，等.谐波干扰下海上风机结构工作模态识别[J].振动与冲击，2015,34(10):152-156.

DONG Xiaofeng, CHEN Jijian, YANG Min. Operation modal identification of an offshore wind turbine structure under harmonic interference[J]. Journal of Vibration and Shock, 2015,34(10):152-156.

[10] 柏林，彭畅，刘小峰.改进的风力发电机组噪声音调评估方法[J].振动与冲击，2012,31(14):157-163.

BO Lin, PENG Chang, LIU Xiaofeng. Improved method for tonality evaluation of wind turbine noises[J]. Journal of Vibration and Shock, 2012,31(14):157-163.

[11] 郭瑜，秦树人.旋转机械非稳定信号的伪速跟踪阶比分析[J].振动与冲击，2004，23(1):61-69.

GUO Yu, QIN Shuren. Pseudo-speed tracking order analysis for non-stationary vibration signals of rotating machinery[J]. Journal of Vibration and Shock, 2004,23(1):61-69.

[12] 左云波，王西彬，徐小力.循环平稳度在发电机组故障趋势分析中的应用[J].振动、测试与诊断，2009,29(3):292-294.

ZUO Yunbo, WANG Xibin, XU Xiaoli. Application of degree of cyclostation to trand analysis of fault in generator sets[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(3):292-294.

[13] XU X L, ZUO Y B. Fault trend analysis of rotating machine based on degree of cyclostation[C]//Proceedings ICACC. Shenyang: ICALL, 2010:136-138.

[14] AMANNA A, PRICE M, THAMVICHAI R J. Grey systems theory applications to wireless communications[J]. Analog Integrated Circuits and Signal Processing, 2011,69(2/3):259-269.

[15] 郝祖龙，刘吉臻，常太华，等.基于小波变换的热工信号多尺度相关性分析[J].中国电机工程学报，2010,30(14):109-114.

HAO Zulong, LIU Jizhen, CHANG Taihua, et al. Analysis on multi-scale correlation of thermal signal based on wavelet transform[J]. Proceedings of the CSEE, 2010,30(14):109-114.

[16] 张玉良，朱祖超，崔宝玲，等.离心泵起动过程中的外特性实验研究[J].机械工程学报，2013,49(16):147-152.

ZHANG Yuliang, ZHU Zuchao, CUI Baoling, et al. Experimental investigation of external performance of prototype centrifugal pump during startup period[J]. Journal of Mechanical Engineering, 2013, 49(16):147-152.

[17] 郭厚明，行志刚，荆双喜.无量纲参数在矿用低速重载齿轮故障诊断中的应用[J].煤炭科学技术，2006,34(8):28-31.

GUO Houming, XING Zhigang, JING Shuangxi. Dimensionless parameters applied to fault diagnosis of mine low speed heavy loaded gear[J].Cola Sience and Technology, 2006,34(8):28-31.

[18] 左云波，徐小力，王西彬.综合分析的发电机组故障趋势曲线[J].微计算机信息，2008,24(16):163-164.

ZUO Yunbo, XU Xiaoli, WANG Xibin. Trend curve if fault in generator sets based on synthetic analysis[J]. Microcomputer Information, 2008,24(16):163-164.

Non-dimensionalparameterstrendanalysismethodintheearlywarninganddiagnosisofwindturbinegearboxfailures

GU Yujiong1, JIA Ziwen1, YIN Chuantao1, REN Yuting2

(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China; 2.Guohua Energy Investment Limited Company, Beijing 100007, China)

The incipient faut features of wind turbines are usually hard to extract on account of its fluctuant working conditions. A non-dimensional parameters trend analysis method was propsed to deal with the early fault diagnosis of turbine gearboxes. Constant time interval time-domain signals were transformed into uniform angle domain signals by the order resampling, and the dimentionless parameters’ tendencies were used to sense the level of turbine gearbox’s early faults. A model for the early fault diagnosis of turbine gearboxes was created based on the parameters trend analysis, to analyse the lab data and actual failure data. The results show that the method is qualified for the turbine gearbox early faults diagnosis and failure time estimation.

wind turbine gearbox; order resampling; dimentionless parameter; trend analysis; early fault diagnosis

TK83

A

10.13465/j.cnki.jvs.2017.19.032

神华集团科技创新项目(SHJT-12-24);华能集团科学技术项目(HNKJ-H27)；中央高校基本科研业务专项基金(2016XS27)

2016-04-01 修改稿收到日期：2016-07-04

顾煜炯 男，博士，博士生导师，1968年10月生

贾子文 男，博士生，1986年7月生