超深矿井提升机多层缠绕钢丝绳圈间过渡对钢丝绳动张力的影响研究

李晓光，龚宪生，吴水源，罗宇驰

(1.重庆大学 机械传动国家重点实验室,重庆 400044；2.重庆大学 机械工程学院,重庆 400044)

超深矿井提升机多层缠绕钢丝绳圈间过渡对钢丝绳动张力的影响研究

李晓光1,2，龚宪生1,2，吴水源1,2，罗宇驰1,2

(1.重庆大学 机械传动国家重点实验室,重庆 400044；2.重庆大学 机械工程学院,重庆 400044)

针对超深矿井提升机多层缠绕，研究多层缠绕钢丝绳圈间过渡时的加速度变化，运用提升钢丝绳的动张力微分方程和MATLAB中的Simulink模块，建立对称及非对称双折线过渡绳槽下多层缠绕钢丝绳的动张力仿真模型并对仿真结果进行分析比较。结果表明，多层缠绕钢丝绳在圈间过渡时产生的加速度变化会对钢丝绳的动张力产生明显的影响，采用对称式折线绳槽进行圈间过渡时的动张力大于非对称折线绳槽，在提升阶段的后期此现象尤为明显。这些结果对超深井提升系统多层缠绕研究有重要的参考价值。

多层缠绕；圈间过渡；双折线过渡绳槽；动张力

随着经济社会的发展，我国对于矿产资源的需求日益增加，但是浅层矿产资源的逐渐耗尽已经严重制约我国经济的快速发展，深部资源的开采利用已经成为我国的重大发展战略。目前，我国仅对800 m以内的浅层矿井提升设备形成了较为完善的产品设计理论、提升检测和安全标准，但现有传统的单绳缠绕式提升机与多绳摩擦式提升机已不能满足超深井提升(井深>1 500 m)的要求[1]，采用双折线过渡绳槽的多钢丝绳多层缠绕的多点提升组合拓扑结构有望成为超深井提升装备的有效型式，其结构及绳槽形式如图1所示。双折线过渡绳槽分为对称双折线过渡绳槽和非对称双折线过渡绳槽，对称双折线过渡绳槽的两个折线过渡区的圆心角间隔Ψ为180°；而非对称双折线过渡绳槽的布置形式为其中一个折线过渡区在原对称的位置上偏置30°，即圆心角间隔Ψ为150°。目前，超深矿井提升系统钢丝绳缠绕过程中的层间、圈间过渡行为、运行过程中动载荷的产生、传播、消退机制等复杂动力学行为尚不明确，这已成为超深井提升设备研究过程中必须克服的科学技术难题。针对多层缠绕在圈间过渡时的速度变化及其对钢丝绳动张力产生的影响进行研究，以期对超深井提升设备的设计和研发提供理论参考。

(a) 多绳多层缠绕式提升机

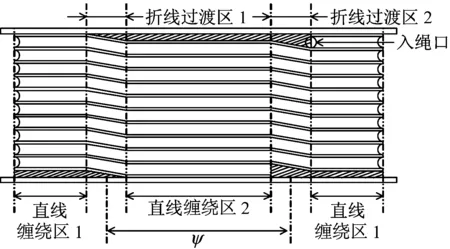
(b) 提升机卷筒绳槽展开图图1 多绳多层缠绕提升机及其绳槽Fig.1 Multi rope and multi-layer winding hoist and its groove

1 提升钢丝绳的数学模型

提升钢丝绳是一种柔性体，在提升过程中提升钢丝绳由于受到加速度以及提升高度变化引起的提升质量变化等外部作用的影响，会产生振幅和频率不断变化的振动，钢丝绳的振动会对于钢丝绳的动张力有明显的影响。

如图2所示，提升机天轮左侧的悬垂段钢丝绳长度是随时变化的，在天轮左侧与钢丝绳的切点处建立坐标系并采用采用瑞利法对提升钢丝绳进行处理，即钢丝绳质量的1/3加到终端质量上，当提升钢丝绳按照图3所示的三段图运动规律进行提升运动时，钢丝绳在加速、匀速和减速三个阶段提升过程中动张力微分方程分别为[2]

2a1·F′)/L1(t)

(1)

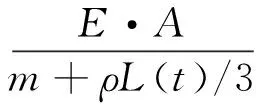
(2)

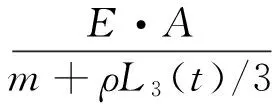
2[v-a2(t-t2)]·F′)/L3(t)

(3)

式中：F为钢丝绳的动张力；a1、a2为提升过程中的加、减速度;E为钢丝绳的杨氏弹性模量；A为钢丝绳的横截面面积;m为钢丝绳提升的重物质量；ν为提升机匀速提升阶段的速度；t1、t2为钢丝绳加速和匀速阶段结束的时间；Ln(t)为各提升阶段钢丝绳的绳长；ρ为钢丝绳单位长度质量。

图2 提升钢丝绳运行示意图Fig.2 Sketch diagram of the operation of hoist rope

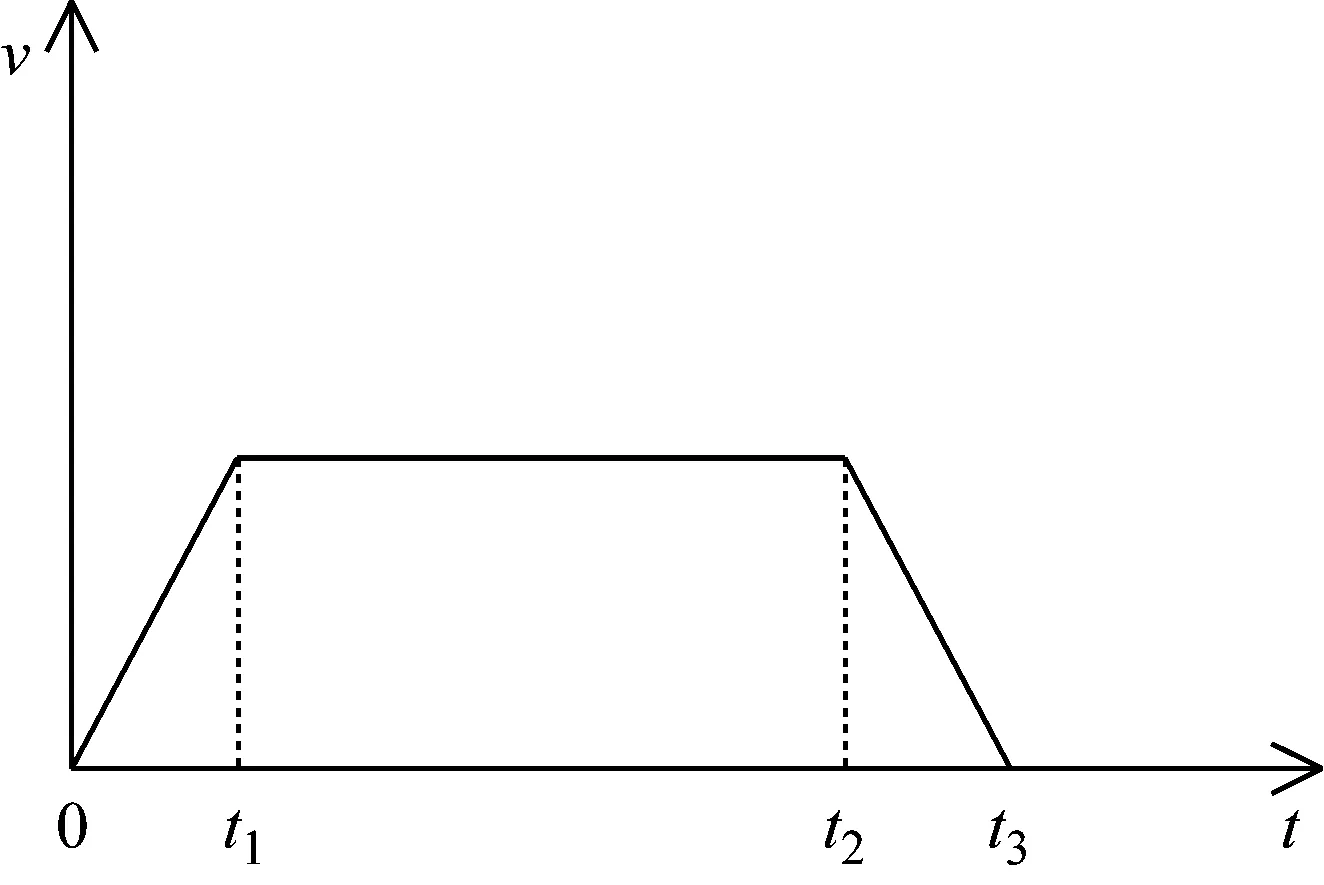
图3 提升速度三段图Fig.3 Hoisting speed of the wire rope

以中信重工提供的试验台数据为依据，提升机试验平台的钢丝绳总绳长为46 m，有效提升距离为43 m，加速及减速提升阶段的加速度值为±0.72 m/s2，匀速提升阶段速度为1.8 m/s，由此计算后可知，加速、匀速和减速阶段的结束时间分别为2.5 s、24 s和26.5 s，钢丝绳绳长Ln(t)在三个提升阶段内的变化为

L1(t)=L-(at2)/2

(4)

(5)

[v·(t-t2)-a(t-t2)2/2]

(6)

式中：t为提升时间；L为钢丝绳总长。

将提升钢丝绳相关参数代入式(4)～式(5)可得

L1(t)=46-0.36·t2(0≤t≤2.5)

(7)

L2(t)=48.25-1.8·t(2.5≤t≤24)

(8)

L3(t)=255.61-19.08·t+0.36·t2

(24≤t≤26.5)

(9)

钢丝绳在多层缠绕时，上层钢丝绳会缠绕在下层两根钢丝绳形成的绳槽内，由于上下层钢丝绳的排绳方向不同，上层的一根钢丝绳圈横跨两个相邻的绳槽，从而产生缠绕过程中的圈间过渡。钢丝绳在圈间过渡时，由于缠绕半径的变化会引起钢丝绳提升速度的变化，尽管速度变化不大，但是由于过渡时间也比较短，所以会有比较大的加速度变化，因此会引起钢丝绳动张力的变化。依据所参照的提升机试验平台，绳槽缠绕宽度为170 mm，绳槽间隙为0.7 mm，缠绕层数为三层，第一层缠绕3圈，第二层缠满12圈，第三层缠绕2圈。由于加速提升阶段较短，此阶段内的钢丝绳尚处于第一层缠绕，此时圈间过渡并不会引起缠绕半径的变化，钢丝绳在第二层缠绕时才会受到圈间过渡加速度的影响。圈间过渡开始出现加速度变化的时间为5.4 s，此时已缠绕的绳长为10.9 m。

由于加速提升阶段不受圈间过渡加速度变化的影响，因此本文主要分析圈间过渡加速度对匀速和减速提升阶段的动张力影响。钢丝绳圈间过渡时的缠绕半径变化如图4所示。

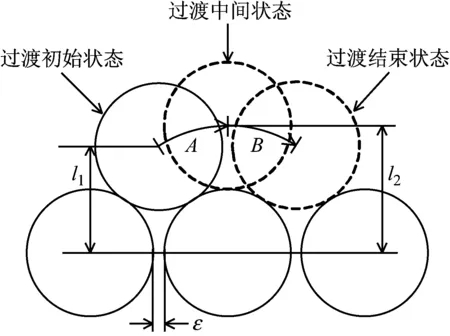
图4 圈间过渡时的缠绕半径变化Fig.4 The variation of the winding radius during the transition between the circles

由于圈间过渡时钢丝绳缠绕产生的半径差相对卷筒直径要小得多，且过渡区很小，若按照几何特征计算将变得非常繁琐且计算的结果差别不大，为了计算方便，只考虑圈间过渡时的平均加速度。

钢丝绳圈间过渡时会的速度差为

Δv=(l2-l1)·ω

(10)

钢丝绳绕过折线过渡区的时间为

Δt=θ/ω

(11)

因此圈间过渡时的平均加速度值为

(12)

(13)

l2=2r

(14)

式中：ω为提升机卷筒缠绕的角速度；θ为折线绳槽对应的圆心角；r为钢丝绳半径；ε为绳槽间隙。

当钢丝绳圈间过渡处于图4中的A阶段时加速度为正，处于B阶段时加速度为负。

由提升机试验台数据可知，提升机卷筒缠绕的角速度为4.5 rad/s，折线绳槽对应的圆心角为π/10，将提升机的数据代入式(14)中得到，钢丝绳在折线过渡区的加减速度值为±0.173 m/s2。

钢丝绳每缠绕一圈所用的时间T为

T=2π·R/v

(15)

对称式绳槽每圈缠绕会出现两次加速度变化，其间隔相等，所以将其看作周期为T/2的信号；非对称绳槽由于两个折线过渡区不对称，其加速度变化的时间间隔为

ΔT=(150°/360°)·T=5T/12

(16)

所以需要将加速度变化看作两个周期为T的信号叠加，两者出现的时间差为5T/12。圈间过渡加速度在提升机匀速提升阶段内的变化形式如图5所示。

(a)非对称双折线圈间过渡(b)对称双折线圈间过渡

在提升机的减速提升阶段，由于提升速度的逐渐减小，钢丝绳在圈间过渡时的加速度也会逐渐减小，其变化形式如图6所示。

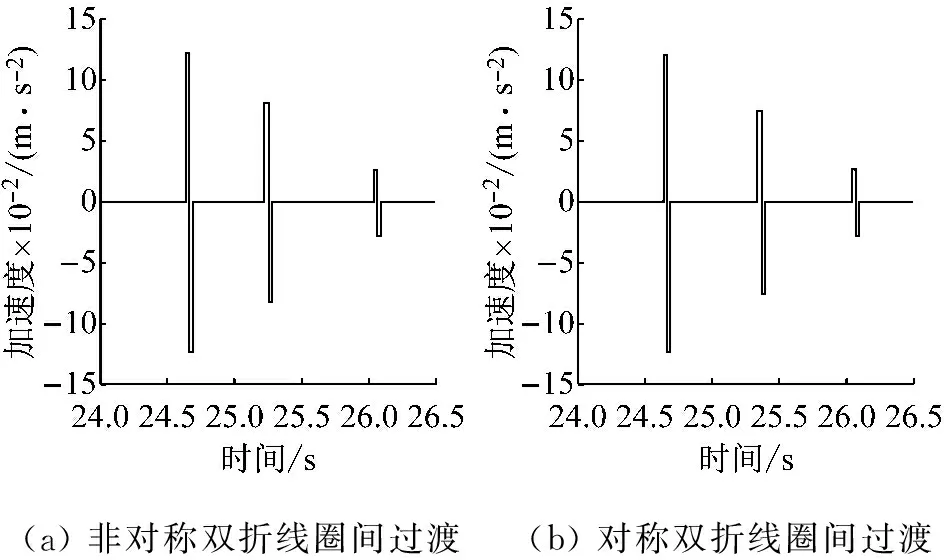
(a)非对称双折线圈间过渡(b)对称双折线圈间过渡

2 钢丝绳动力学建模

本文选取直径10 mm的6×7+IWS钢丝绳为研究对象，经过计算和查询[3-4]，得到动张力微分方程相关参数如表1所示。

依据式(1)～式(3)，并结合钢丝绳的实际参数，建立无圈间过渡、对称双折线圈间过渡和非对称双折线圈间过渡三种状态下的Simulink动张力仿真模型。以非对称双折线圈间过渡动张力仿真模型为例，图7为钢丝绳加速、匀速及减速阶段的动张力输出图，模型中clock模块控制模型运行的总时间，内部设置2.5 s和24 s作为各提升阶段动张力输出的判别条件，模型中的u为运行时间；图8为钢丝绳各阶段绳长的输出图，模型内部同样以2.5 s和24 s为各阶段绳长公式计算的判别条件，模型中u为运行时间；图9为匀速阶段的动张力计算模型，模型采用两个generator模块叠加作为非对称双折线圈间过渡的加速度信号并依据匀速提升阶段的绳长等参数对微分方程进行数值仿真。无圈间过渡和对称双折线圈间过渡状态下的建模过程与之类似，故在此不再一一列举。

表1 动张力微分方程相关参数Tab.1 The related parameters of dynamic tension differential equation

图7 钢丝绳动张力模型Fig.7 Simulationmodelofthewireropedynamicforce图8 钢丝绳绳长变化模型Fig.8 Simulationmodeloftheropelength

图9 钢丝绳匀速运行阶段动张力模型Fig.9 Simulation model of the wire rope dynamic force in the uniform phase

本文中依据提升过程时间设定仿真时长为26.5 s，采用变步长解算器并采用四阶龙格库塔算法。

3 计算结果及分析

运行计算动张力的Simulink模型，得到无圈间过渡、对称双折线圈间过渡和非对称双折线圈间过渡三种情况下的动张力变化曲线如图10所示。

如图10(a)～图10(c)所示，三种状态下钢丝绳的动张力变化趋势大致相同。在提升过程中，钢丝绳的动张力有明显的波动，动张力总体呈下降趋势，这是由于提升过程中钢丝绳的长度减小造成的提升重量和等效刚度的不断变化引起的；同时，钢丝绳在加速到匀速和匀速到减速两个过渡阶段内的动张力都出现了较大的突变，其原因为钢丝绳在各提升阶段的加速度变化引起的惯性载荷和冲击造成的；另外，在提升过程中，钢丝绳动张力的波动频率不断增大，这是由于提升过程中钢丝绳的长度不断减小造成钢丝绳的振动产生了变化[5-12]。

通过对比图10(a)～图10(c)三条曲线可知，多层缠绕钢丝绳在圈间过渡时的加速度变化对加速提升阶段几乎没有影响，但是对匀速和减速提升阶段有较明显的影响。如图10(a)，如果不考虑圈间过渡，在匀速提升阶段钢丝绳动张力波动逐渐减小，减速提升阶段动张力的振幅很小几乎呈一种直线状态，因为此时引起动张力变化的因素只有钢丝绳的长度变化。考虑多层缠绕钢丝绳的圈间过渡加速度以后，钢丝绳的动张力会有明显的不同，在提升阶段后期钢丝绳的动张力波动并不会明显的减小，而是处于一种周期性变化的振动状态。对比图10(b)和图10(c)两种双折线过渡方式的动张力曲线可知，在加速提升阶段，非对称双折线钢丝绳动张力和对称双折线钢丝绳动张力没有明显的区别，在匀速提升阶段，从大约第8 s开始，非对称双折线圈间过渡动张力相较于对称双折线圈间过渡动张力波动幅度更小，在减速提升阶段，非对称双折线圈间过渡钢丝绳动张力波动幅度相较于非对称双折线圈间过渡波动幅度以更快的速度减小且以较大幅度波动所持续的时间很短。

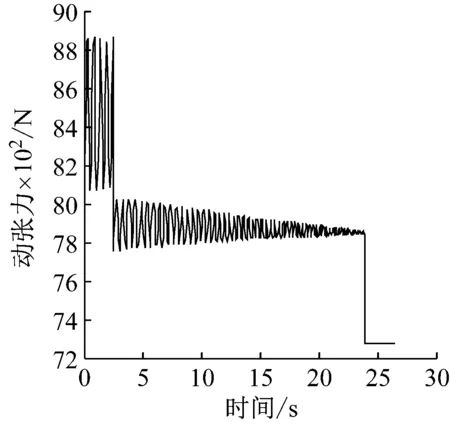
(a) 无圈间过渡

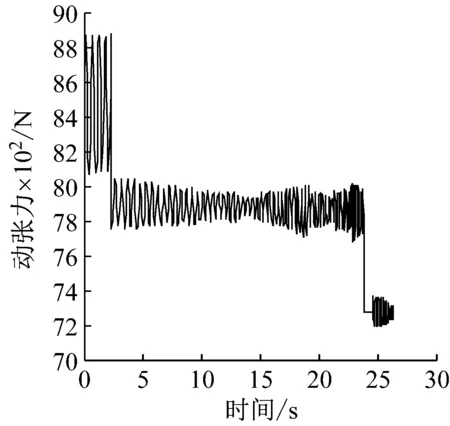
(b) 对称双折线圈间过渡

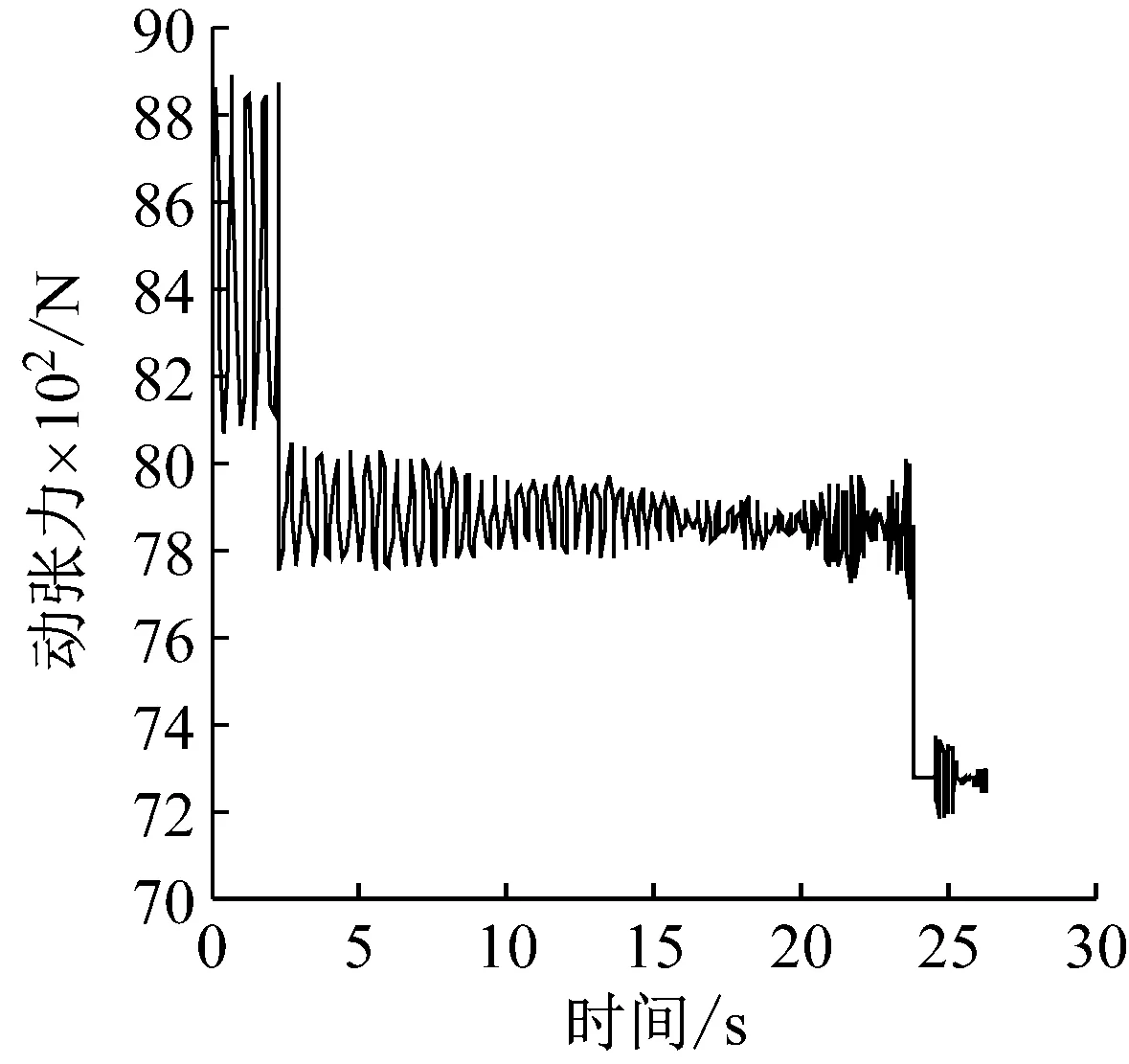
(c) 非对称双折线圈间过渡图10 钢丝绳动张力变化曲线Fig.10 Evolution of the rope load with time

4 结 论

(1) 本文对多层缠绕钢丝绳进行圈间过渡时的加速度进行计算，并结合钢丝绳在提升过程中的动张力微分方程，建立了提升过程中钢丝绳动张力的Simulink仿真模型，得到了钢丝绳动张力变化曲线。

(2) 通过对钢丝绳动张力的变化曲线进行比较，发现多层缠绕钢丝绳圈间过渡时的加速度变化对钢丝绳的动张力有明显的影响，在分析过程中不能忽略。

(3) 采用双折线过渡绳槽进行多层缠绕钢丝绳圈间过渡时，非对称双折线圈间过渡比对称双折线圈间过渡的动张力波动幅度更小，且出现动张力波动较大的范围持续时间较短，此现象在提升过程的后期尤为明显。

(4) 以本文方法得到的钢丝绳圈间过渡动张力波动曲线，并未将钢丝绳阻尼、钢丝绳与卷筒之间的摩擦等影响因素考虑在内，故动张力波动曲线存在一定的偏差，因此今后还需通过试验作进一步的研究。

[1] 聂虹.矿井提升机的发展与现状[J]. 矿山机械, 2015，43(7)：13-17.

NIE Hong. Development and current situation of mine host[J]. Mining & Processing Equipment, 2015，43(7)：13-17.

[2] 严世榕, 闻邦椿. 竖井提升钢丝绳容器系统在提升过程中的动力学仿真[J]. 中国有色金属学报, 1998(增刊2):618-622.

YAN Shirong, WEN Bangchun. Dynamic simulation of shaft hoisting rope container system in the process of hoisting[J]. Transactions of Nonferrous Metals Society of China, 1998(Sup2):618-622.

[3] 国家质量监督检验检疫总局.重要用途钢丝绳：GB 8918—2006[S].北京：国家标准化管理委员会，2006.

[4] VANDERVELDT H H, CHUNG B S, READER W T. Some dynamic properties of axially loaded wire ropes[J]. Experimental Mechanics, 1972, 13(1):24-30.

[5] 包继虎, 张鹏, 朱昌明. 变长度提升系统钢丝绳纵向振动特性[J]. 振动与冲击, 2013, 32(15):173-177.

BAO Jihu, ZHANG Peng, ZHU Changming. Longitudinal vibration of rope hoisting systems with time-varing length[J].Journal of Vibration and Shock, 2013,32(15):173-177.

[6] ZHU W D, NI J. Energetics and stability of translating media with an arbitrarily varying length[J]. Journal of Vibration & Acoustics, 2000, 122(3):295-304.

[7] 吴娟, 寇子明, 梁敏. 摩擦提升系统钢丝绳横向动力学分析[J]. 振动与冲击, 2016, 35(2):184-188.

WU Juan, KOU Ziming, LIANG Min. Transverse dynamics analysis of rope in multi-rope friction hoisting system[J]. Journal of Vibration and Shock, 2016, 35(2):184-188.

[8] CARTMELL M P, MORRISH L, TAYLOR A J. Dynamics of spreader motion in a gantry crane[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989-1996 (vols 203-210), 1998, 212(2): 85-105.

[9] 贾尚雨, 谢小鹏, 梁广炽. 起重机钢丝绳的动力学建模与仿真[J]. 煤矿机械, 2010, 31(4):58-61.

JIA Shangyu, XIE Xiaopeng, LIANG Guangchi. Dynamics modeling and simulation of crane wire rope[J].Coal Mine Machinery, 2010, 31(4):58-61.

[10] 严世榕,闻邦椿.下放容器时提升钢丝绳的动力学仿真[J].煤炭学报,1998,23(5):530-534.

YAN Shirong, WEN Bangchun. Dynamic simulation of hoisting wire rope in the descending cycle of container[J]. Journal of China Coal Society,1998,23(5): 530-534.

[11] 刘会灯. MATLAB编程基础与典型应用[M]. 北京：人民邮电出版社, 2008.

[12] 杨义勇, 金德闻. 机械系统动力学[M]. 北京：清华大学出版社, 2009.

Influenceofropecircletransitiononthedynamictensionofmultilayerwindingwireropesinsuperdeepminehoistingmachines

LI Xiaoguang1,2，GONG Xiansheng1,2，WU Shuiyuan1,2，LUO Yuchi1,2

(1.The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China; 2.College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)

The acceleration variation during the rope circle transition of multi-layer windings in super deep mine hoists was studied. With the aid of the differential equation for the dynamic tension of lifting wire ropes and the MATLAB Simulink module, the dynamic tension of a multi-layer winding wire rope with symmetric and non symmetric bilinear transitional rope slots was modeled, simulated and analyzed. The results show that the acceleration during the rope circle transition of the multi-layer winding wire rope has a significant impact on the dynamic tension of the wire rope. The dynamic tension of the rope with the circle transition in the symmetrical bilinear rope groove is larger than that in the non symmetrical bilinear rope groove. The results are of reference value for the study of multi-layer windings of super deep well lifting systems.

multi-layer winding; transiting; double broken line transition rope slot; dynamic tension

TH113

A

10.13465/j.cnki.jvs.2017.19.038

国家重点基础研究发展计划(973计划)资助项目(2014CB049403)

2016-05-10 修改稿收到日期：2016-08-13

李晓光 男，硕士生，1990年生

龚宪生 男，博士，教授，博士生导师，1956年生