高速电主轴铣削稳定性研究
2017-11-06单文桃陈小安王洪昌俞成涛
单文桃,陈小安,王洪昌,俞成涛
(1. 江苏理工学院 机械工程学院,江苏 常州 213001;2. 重庆大学 机械工程学院,重庆 400044)
高速电主轴铣削稳定性研究
单文桃1,陈小安2,王洪昌1,俞成涛1
(1. 江苏理工学院 机械工程学院,江苏 常州 213001;2. 重庆大学 机械工程学院,重庆 400044)
建立了高速电主轴轴承-转子动力学模型,并分析高转速与铣刀刀尖点处传递函数的关系,以此为基础建立高速电主轴铣削稳定性模型。以D62D24A型高速电主轴为例,针对转速对轴承动态支承刚度的“弱化”作用,计算系统第一阶径向振动固有振型,理论分析并经实验验证系统第一阶径向振动固有频率的变化趋势,并解析转速影响下的系统铣削稳定瓣图,实验验证了高转速下系统铣削稳定性能的变化趋势。
高速电主轴;动力学模型;铣削稳定性
高速加工是国际机械制造业最热门的研究课题之一[1],高速电主轴作为高速数控机床的核心功能部件,其切削稳定性能直接影响高速加工的质量。铣削是电主轴最常应用的加工方式,对高速电主轴铣削稳定性能的研究十分必要。
高速电主轴系统动力学特性对其铣削稳定性能产生直接影响,许多学者建立了电主轴轴承-转子动力学模型,研究了系统的刚度、固有振型、固有频率和动态响应等特性。Terman等[2]以简单的欧拉梁理论为基础,将轴承等效成定刚度弹簧,运用有限差分方法求解了轴承-转子系统的动力学方程。Sharan等[3]建立同样的模型,并运用有限单元法分析了轴承转子系统在随机载荷作用下的动态响应。考虑入陀螺力矩和离心力载荷的影响,Shin[4]分析了高速角接触球轴承的“软化”现象,而这种现象会导致轴承-转子系统第一阶固有频率的下降[5-7]。Nelson[8]应用考虑入剪切效应和陀螺力矩效应的Timoshenko梁理论,结合有限元方法,建立了Timoshenko梁的有限元模型,Li等[9-10]运用此模型建立了高速电主轴热-机耦合动力学模型,详细阐述了热膨胀对轴承预紧力变化和内部几何相容关系的影响,设计了整体模型的迭代计算流程,并且通过实验验证了热膨胀因素影响下的高速电主轴系统的前两阶固有频率的变化趋势。
对于铣削稳定性能的研究之前,动态切削力模型的研究必不可少,Engin等[11-12]建立了动态切削力与瞬时切削厚度的线性函数,提出线性切削力模型,Faassen等[13]提出了一种考虑后刀面与被加工表面“刃口效应”的非线性切削力模型,在考虑进给量对延迟时间的影响基础之上,根据铣刀的结构特点,梁睿君等[14]分析了微元铣削力与瞬时切屑厚度之间的线性关系,建立了螺旋圆柱铣刀的动态切削力模型。在切削力模型研究的基础之上,Alnold认为切削力的主分力相对于切削速度的下降特性很容易引起切削过程的自激振动,即“摩擦颤振”[15],他还给出了切削时上一次由于偶然原因产生的振纹会激起下一次切削中的振动,只要前后两次切削时振动的相位合适就可能会对动态切削力产生很大的影响,即“再生颤振”[16]。蒋宇平等[17]通过对切屑厚度、铣削力建模,建立了薄壁件铣削系统动力学模型,考虑了薄壁件铣削稳定性受铣削位置影响,揭示稳定铣削与不稳定铣削、不同模态在不稳定铣削时铣削力、铣削位移的变化规律。
以上研究对高速电主轴动力学特性和铣削稳定性能分别有着较为深入的研究,但是对于当前高端数控机床高速铣削的稳定性问题不能给予解决,如高转速对电主轴自身动力学性能、铣刀刀尖点处传递函数及铣削稳定性能的影响等问题。针对以上观点,本文以高速电主轴动力学特性研究为基础,分析了高转速与铣削稳定性之间的关系,建立了铣削刀尖点处的传递函数模型,并且对高转速影响下的电主轴铣削稳定性能进行了理论分析和实验验证。
1 动力学建模
1.1轴承模型
图1表示轴承内部几何相容关系,高速运行的角接触球轴承在轴向预紧载荷Fa、径向载荷Fr以及弯矩载荷M的联合作用下,内、外圈会发生相对轴向位移δa、径向位移δr和角位移θ,图中r为径向方向,a为轴向方向,E、E′分别为轴承运行前、后钢球球心,m、m′分别为轴承运行前、后内沟道曲率中心,n为外沟道曲率中心,位置固定。
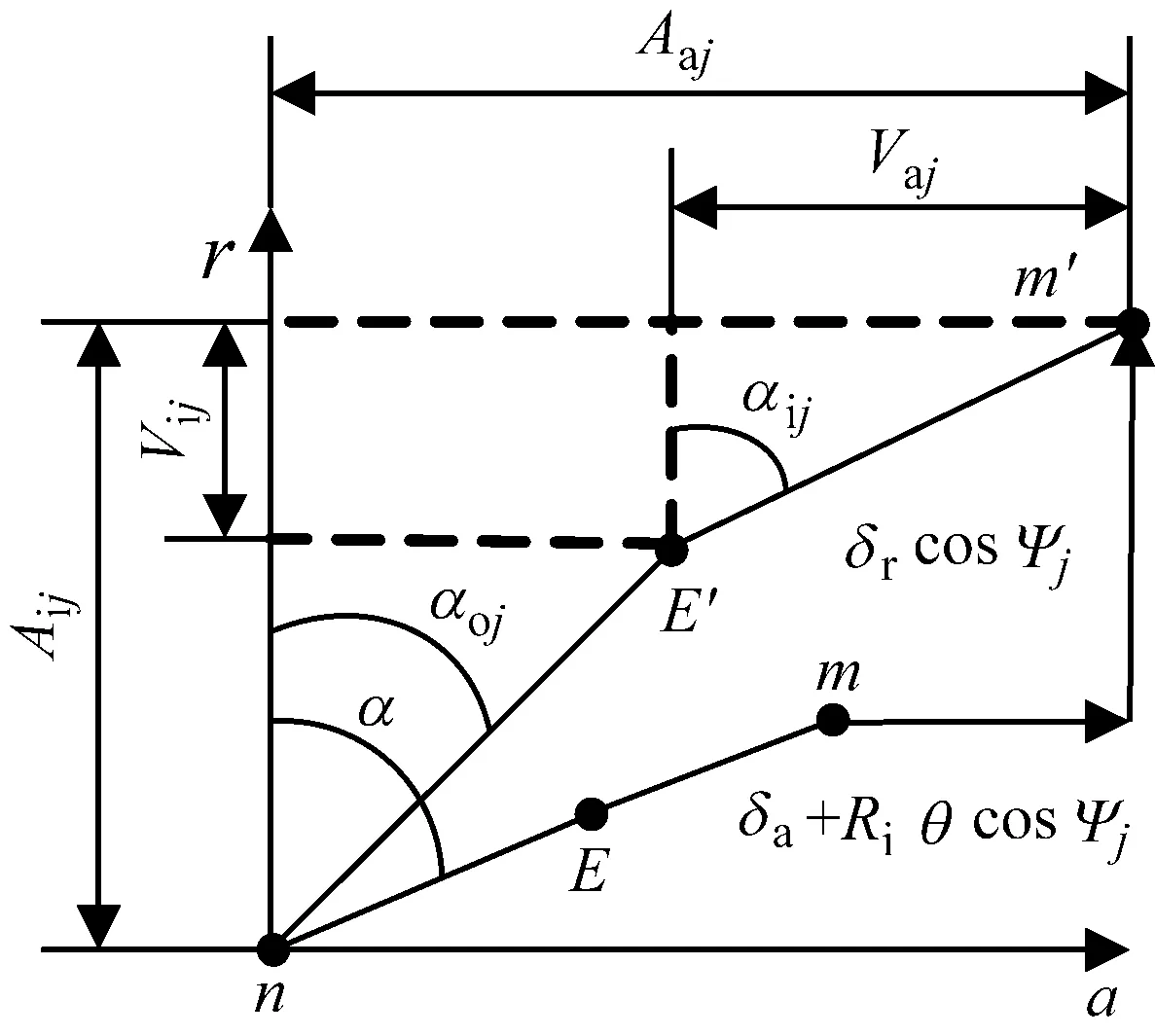
图1 轴承内部几何相容关系Fig.1 Compatible geometry of mapping inside bearing
钢球角位置为Ψj处的内沟道曲率中心的坐标为
Aaj=Bdbsinα+δa+RiθcosΨj
Arj=Bdbcosα+δrcosΨj
(1)
式中:B=fi+fo-1;fi、fo分别为内、外沟道曲率半径系数;db为钢球直径;α为初始接触角;Ri为内沟道中心圆半径;Vaj、Vrj为角位置为Ψj处钢球球心位置参数。
分析其几何相容关系,可以得到相容方程
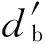
(2)
式中:δij、δoj为角位置为Ψj处钢球与内、外沟道的Hertz接触弹性形变量。
根据轴承套圈控制理论,不考虑公转打滑和陀螺旋转的影响[18],对钢球进行拟静力学受力分析如图2所示,可以得到角位置Ψj处钢球的拟静力平衡方程
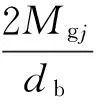
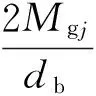
(3)
式中:Qij和Qoj为角位置Ψj处钢球和内、外圈的接触力;αij、αoj为钢球与内、外圈滚道的实际接触角;Fcj为高转速下钢球的离心力;Mgj为高转速下钢球的陀螺力矩。
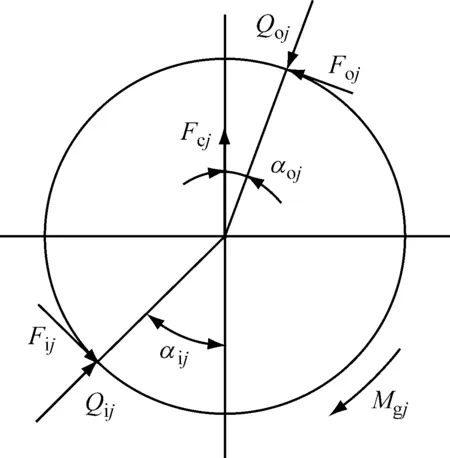
图2 钢球受力分析Fig.2 Quasi static analysis of ball
对轴承内圈进行拟静力学受力分析可以得到如下平衡方程
(4)
式中,Z为钢球数目。
联合求解以上方程可得角接触球轴承动态支撑刚度,其矩阵形式为[19]
Fb=Kbδb
(5)
式中:Fb为轴承内圈载荷向量;Kb为轴承支承刚度矩阵;δb为轴承内圈位移向量。
1.2轴承-转子模型
高速电主轴的轴承固接于壳体,同时轴承支承主轴高速运转,刀具由刀夹或者拉刀机构固接于主轴前端。应用Timoshenko梁理论[20]和有限元理论[21],将质量连续、无限多自由度的主轴和铣刀划分成质量离散、具有有限多自由度的有限元模型,将轴承简化成非线性支承弹簧,建立系统整体的轴承-转子动力学模型,其方程为
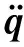
[K+Kb-ω2Mc]{q}={F}
(6)
式中:M为系统质量矩阵;C为系统阻尼矩阵;G为系统陀螺矩阵;Mc为系统离心质量矩阵;{F}为切削载荷向量;{q}为轴节点位移向量;ω为轴转动角速度。
2 铣刀刀尖点传递函数
系统动力学模型中相应矩阵非对角元素不全为零,在物理坐标下方程不能完全解耦,求解刀具与被切削材料接触点处的传递函数较为困难。而分析系统的动态特性往往只需要前几阶模态即可,所以,将物理坐标下的系统动力学模型转换到模态坐标下是非常必要的,通过降阶后的模型求解将更加简单、有效。
将式(6)等号右边的切削外载荷F项写成切削点分布向量与切削力大小相乘的形式,如下
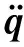
[K+Kb-ω2Mc]{q}=F={b}F
(7)
式中:{b}为刀具切削点分布输入向量;F为刀具切削点处切削力。
假设系统模态坐标向量为{ξ},则
{q}=Φ{ξ}
ΦTMΦ=I;ΦT(C-2ωG)Φ=diag(2ζiωi);
(8)
式中:Φ为系统归一化的振型矩阵;ζi为第i阶模态阻尼比;ωi为第i阶模态固有角频率。式(8)变换到模态坐标下为
(9)
设状态向量

(10)
则系统动力学方程可以写成状态方程的形式
(11)
式中:Am为系统状态矩阵;Bm为系统输入矩阵。
写出系统输出方程,当输出为系统振动位移或者振动速度时
(12)
当输出为系统振动加速度或者振动速度时
Cm{X}+DmF
(13)
式中:{c}为切削点分布输出向量;Cm为系统输出矩阵;Dm为系统前置矩阵。
假设求解切削点处第v个自由度上输入到第u自由度上输出的传递函数,可以调整向量{b}第v个数值为1,其他全部为0,调整向量{c}中第u个数值为1,其他全部为0,得到传递函数如下
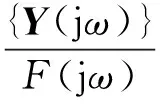
(14)
3 铣削稳定性建模
本文的铣削力采用瞬时刚性力模型,铣削形式为圆柱铣刀圆周铣削,其中包括顺铣和逆铣,切削深度为ac,切削厚度为bc。
稳定性模型采用Altintas等的铣削稳定性模型,如图3所示,动态铣削力与颤振位移的关系为
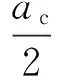
(15)
式中:Fd(t)={Fdx(t)Fdy(t)}T;r(t)={x(t)y(t)}T;r(t-T) = {x(t-T)y(t-T)}T;T为铣削周期;A0为与时间无关、只与切削参数有关的常数矩阵。
Fd(t)与r(t)在频域范围内存在关系
(16)
则
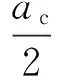
(17)
式(17)存在奇异解的条件为
(18)
式(18)为计算条件,可以得出铣削颤振角频率为ωc的临界切削厚度
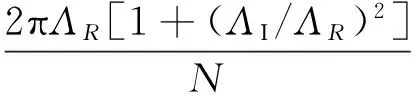
(19)
式中:ΛR和ΛI为与铣削参数和铣刀刀尖点处传递函数有关的变量,N为铣刀刀齿数。相应的,铣削颤振角频率为ωc时的临界转速为

(20)
式中:k= 0,1,2,… 为系统稳定叶瓣数;τ=π-2arctan(ΛI/ΛR)为颤振振痕的相位差。
通过选定的颤振角频率ωc,并且根据式(19)和式(20)确定此颤振角频率处的临界切削深度和临界转速,不断变化ωc重复上述过程即可得到系统铣削稳定性叶瓣图。
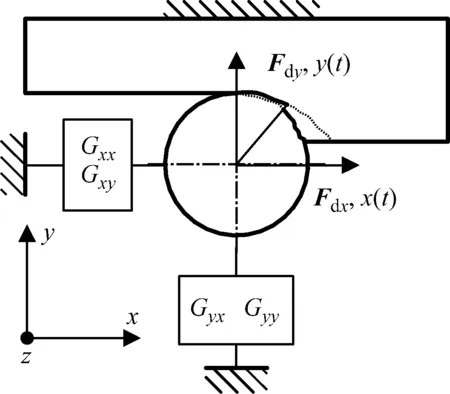
图3 铣削稳定性模型Fig.3 Stability model of milling
4 理论分析与实验研究
本文分析对象为D62D24A型高速电主轴,结构简图如图4所示,其转速、电机功率、系统冷却、轴承润滑、轴承预紧等基本参数见表1,铣刀参数见表2。
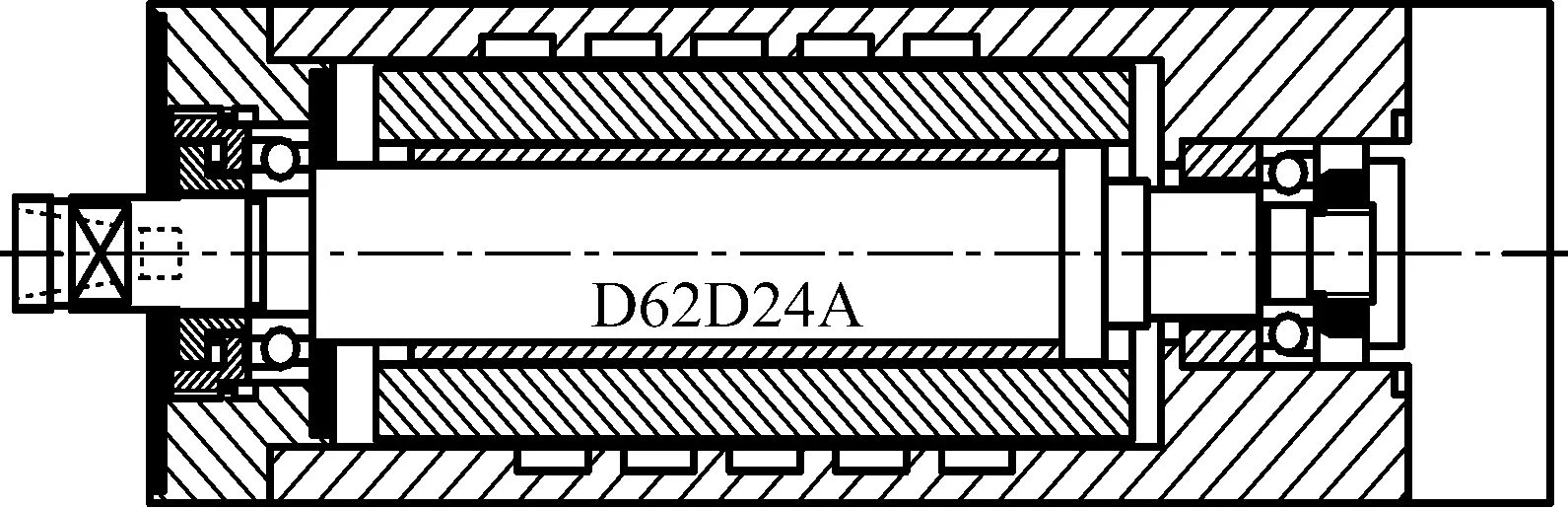
图4 电主轴系统结构简图Fig.4 Schematic of motorized spindle system
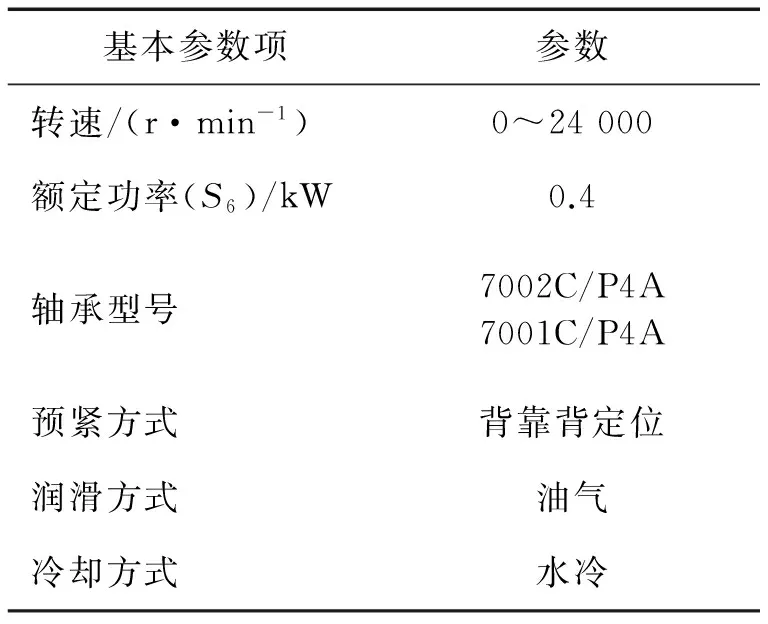
表1 电主轴基本参数Tab.1 Basic parameters of motorized spindle
4.1轴承动态支承刚度
高速运转的角接触球轴承,其刚度矩阵对角线元素对电主轴铣削稳定性能起着关键性作用,其中径向刚度对其影响最为直接。
转速是影响轴承支承刚度的重要因素,图5表示转速对轴承径向刚度的影响。不难看出,随着转速的升高,轴承的径向刚度大幅度降低,这是由于钢球离心力和陀螺力矩对轴承刚度的软化作用,这会反映到电主轴系统整体的动力学特性和铣削稳定性能当中。
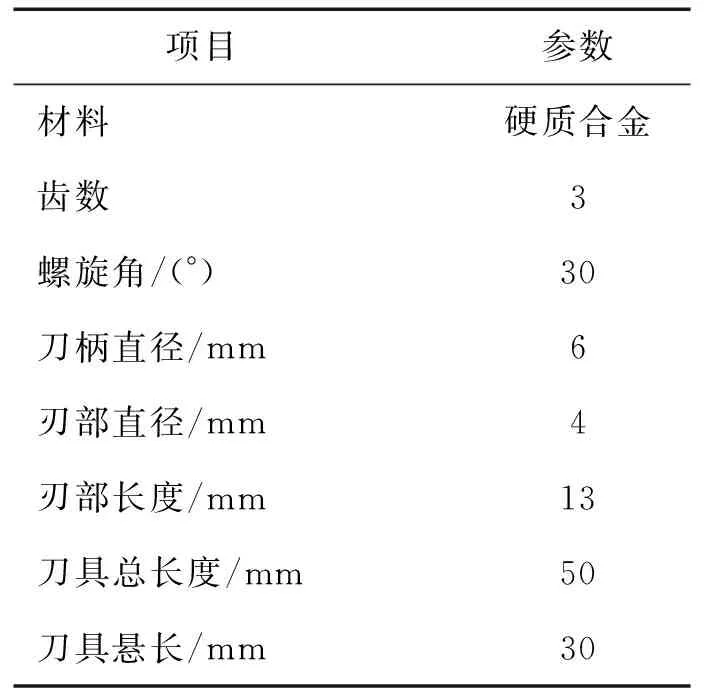
表2 铣刀参数Tab.2 Milling cutter parameters

图5 转速对轴承径向刚度的影响Fig.5 Effect of speed on bearing radial stiffness
4.2轴承-转子动力学特性
根据上述动力学建模方法,结合D62D24A型高速电主轴结构特点,应用Timoshenko梁理论和有限元理论,建立系统有限元动力学模型,如图6所示。主轴和铣刀通过轴承与壳体相连接,把轴承简化成非线性弹簧,提供径向、轴向和横向转动方向的刚度,铣刀与主轴通过刀夹相固接,振动自由度完全耦合,主轴上附属零部件等效成附加质量圆盘。
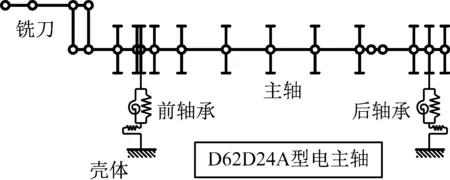
图6 轴承-转子有限元动力学模型Fig.6 Finite element dynamic model of bearing-rotor system
高速电主轴第一阶固有特性为系统最重要、最明显的基本特性,不但决定着电主轴的极限转速,也对系统铣削稳定性产生很大的影响。图7所示为D62D24A型电主轴第一阶径向振动固有振型,为主轴和铣刀的弹性体振动,最大相对振幅出现在主轴中部和铣刀刀尖点处。
电主轴高速运转时,轴承的动态支承刚度会发生变化,这会反映到系统的动力学特性当中。用WD501型电涡流位移传感器测量不同转速下铣刀刀杆最前端的径向振动位移,通过其频谱特性分析轴承-转子系统动力学特性的变化。测试中采样频率为10 000 Hz,采样时间0.1 s,电主轴转速范围10 000~20 000 r/min,部分测试结果如图8所示。由于转子不平衡造成的离心载荷与转速的平方成正比,频率为一倍转频,所以主轴运转时,一倍转频处出现较大幅值;与此同时,频谱的二倍转频处也出现峰值,其原因很可能是电机的电磁不平衡拉力对转子的作用结果[22];外部噪声信号会引起频谱中固有频率处的峰值,并且随着转速的升高,第一阶径向振动固有频率会随之减小,这是由于轴承支承刚度随转速升高而降低的原因。
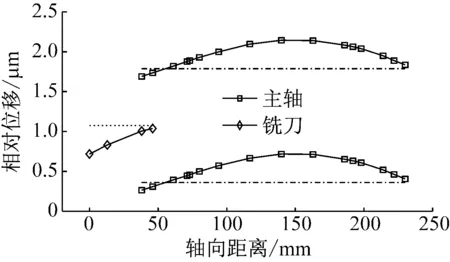
图7 第一阶径向振动固有振型Fig.7 First order natural modal shapes of radial vibration
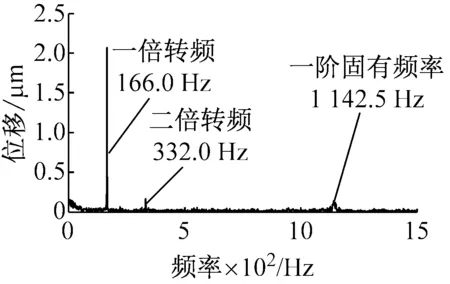
(a) 10 000 r/min
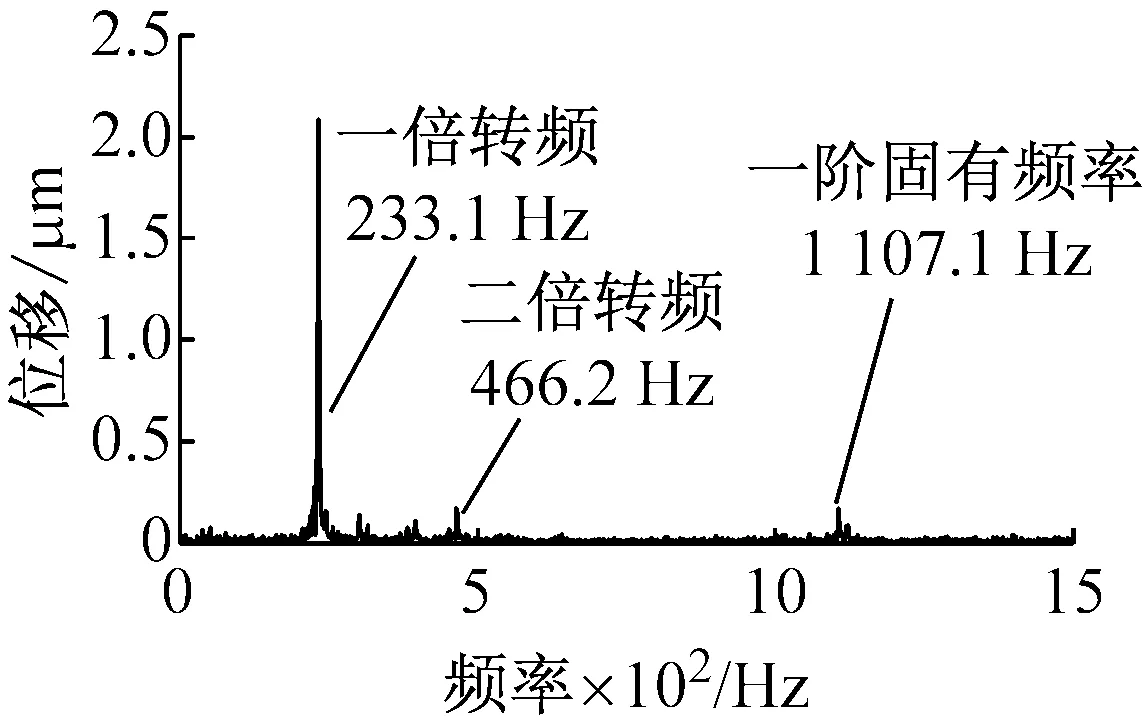
(b) 14 000 r/min
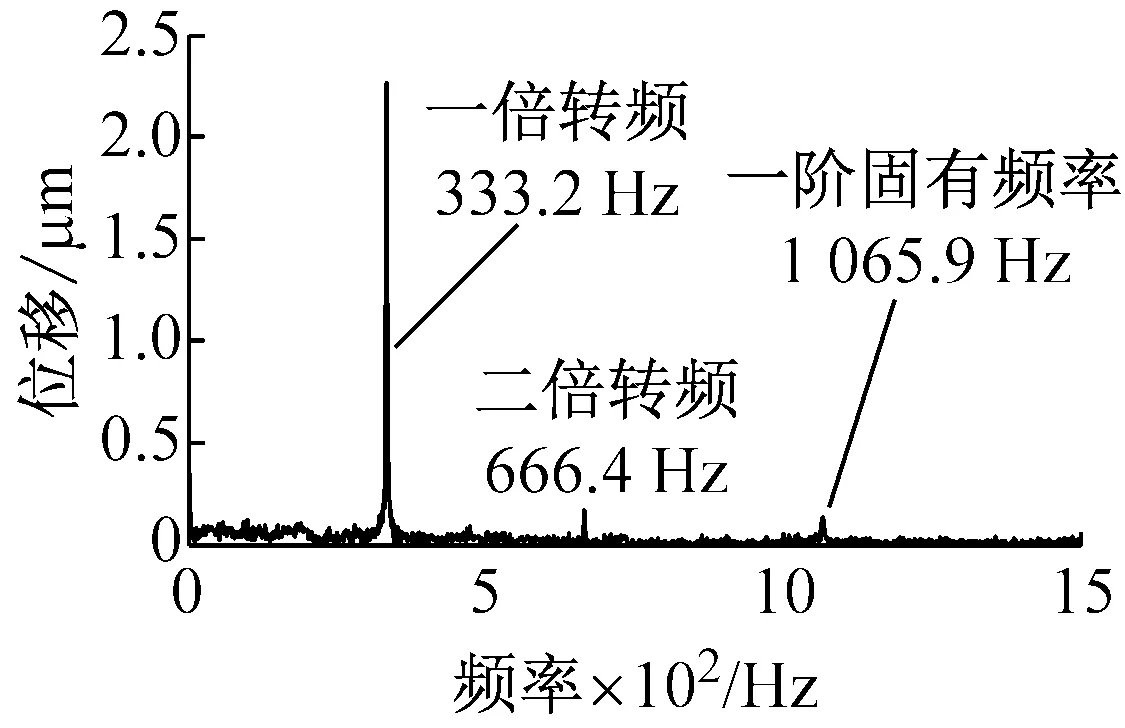
(c) 20 000 r/min图8 电主轴径向振动位移的频谱Fig.8 Frequency spectrums of radial vibration displacement of motorized spindle
图9展示了轴承-转子系统第一阶径向振动固有频率随转速变化的分析结果和实验结果,可以看出,随着转速的升高,第一阶径向振动固有频率不断减小,这种转速对系统固有特性的“弱化”作用将反映到电主轴的铣削稳定性能当中。
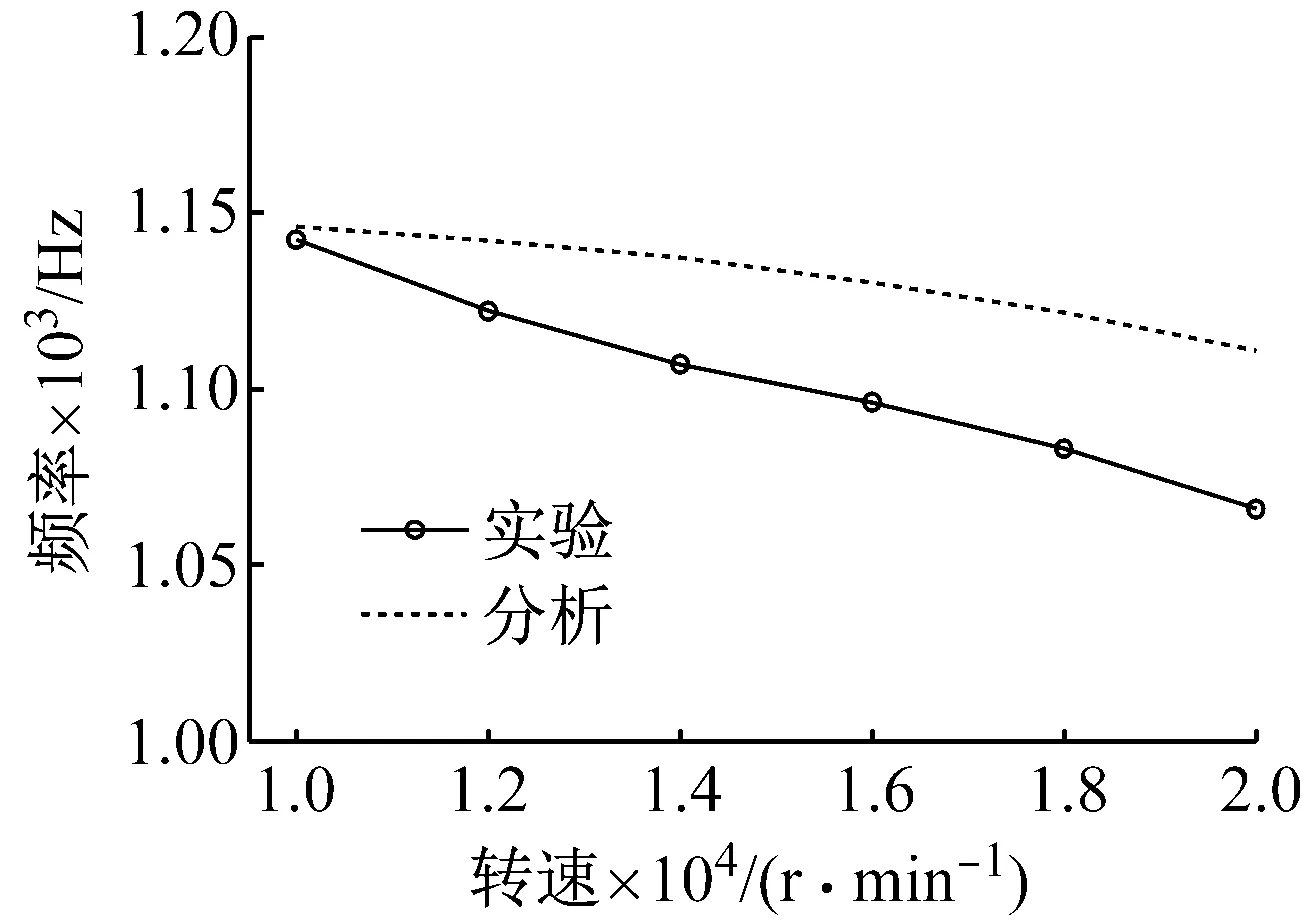
图9 第一阶径向振动固有频率Fig.9 The first order natural frequencies of radial vibration
4.3铣刀刀尖点处传递函数
高速运转下电主轴铣刀刀尖点处传递函数的测试非常困难,但是静态下的测试具有可实施性,其部分测试结果对电主轴高速运转时的刀具刀尖点传递函数有一定借鉴意义。
将D62D24A型电主轴及铣刀安装于Carver_S400型三轴雕刻机床,测试原理如图10所示,用力锤分别激振刀具刀尖点处x和y方向,并且利用力锤配套的力传感器测量激振力,同时利用电涡流传感器测量相应方向上的铣刀振动位移,实验器材参数见表3。
图11所示为铣刀刀尖点处传递函数,在其第一阶固有频率处出现峰值,分别为x方向1 162.1 Hz、y方向1 176.9 Hz,符合图10中系统固有频率的变化趋势,模态固有阻尼比分别为x方向1.52%和y方向1.34%,此结果应用于理论模型,计算铣刀相同位置处的传递函数,与实验结果相比较基本一致。电主轴运转过程中的模态固有阻尼比测量困难,可以用静态时测试结果近似替代。

图10 刀具刀尖点处传递函数测试示意图Fig.10 Test schematic of transfer functions at milling cutter
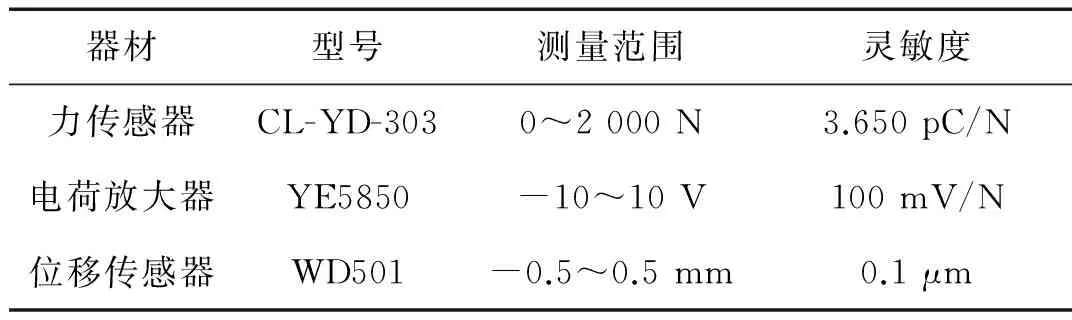
表3 测试参数Tab.3 Test parameters
由于高速运转的电主轴系统动力学特性会受到转速的影响,所以铣刀刀尖点处的传递函数也会受到转速“弱化”作用的影响。图12表示考虑转速影响与不考虑转速影响的情形下电主轴铣刀刀尖点处x方向的传递函数分析结果,可以看出:随着转速的升高,轴承径向支承刚度减小,轴承-转子系统第一阶固有频率降低,铣刀刀尖点处传递函数峰值也会向低频方向移动,且幅值有所增大。
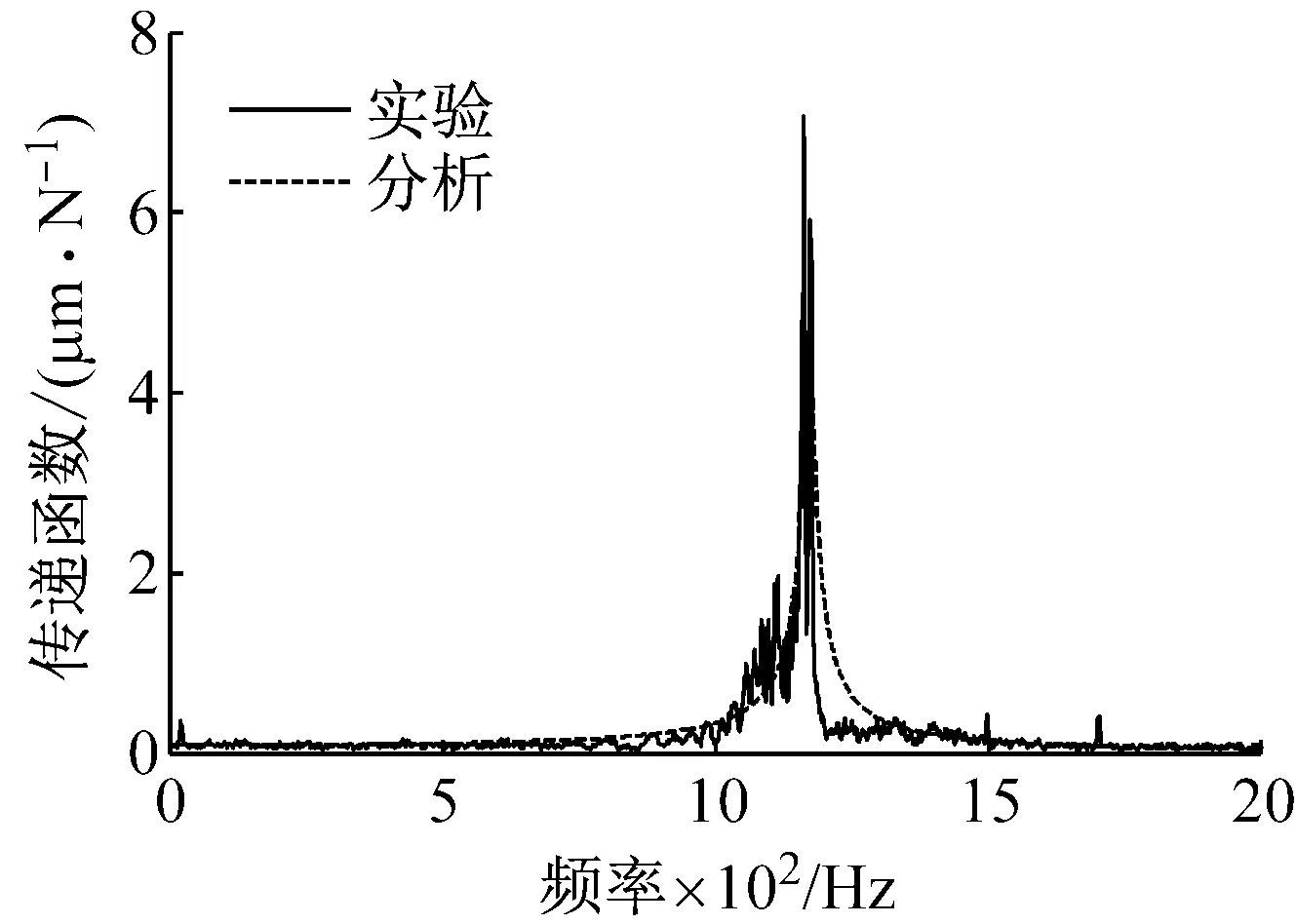
(a) x方向
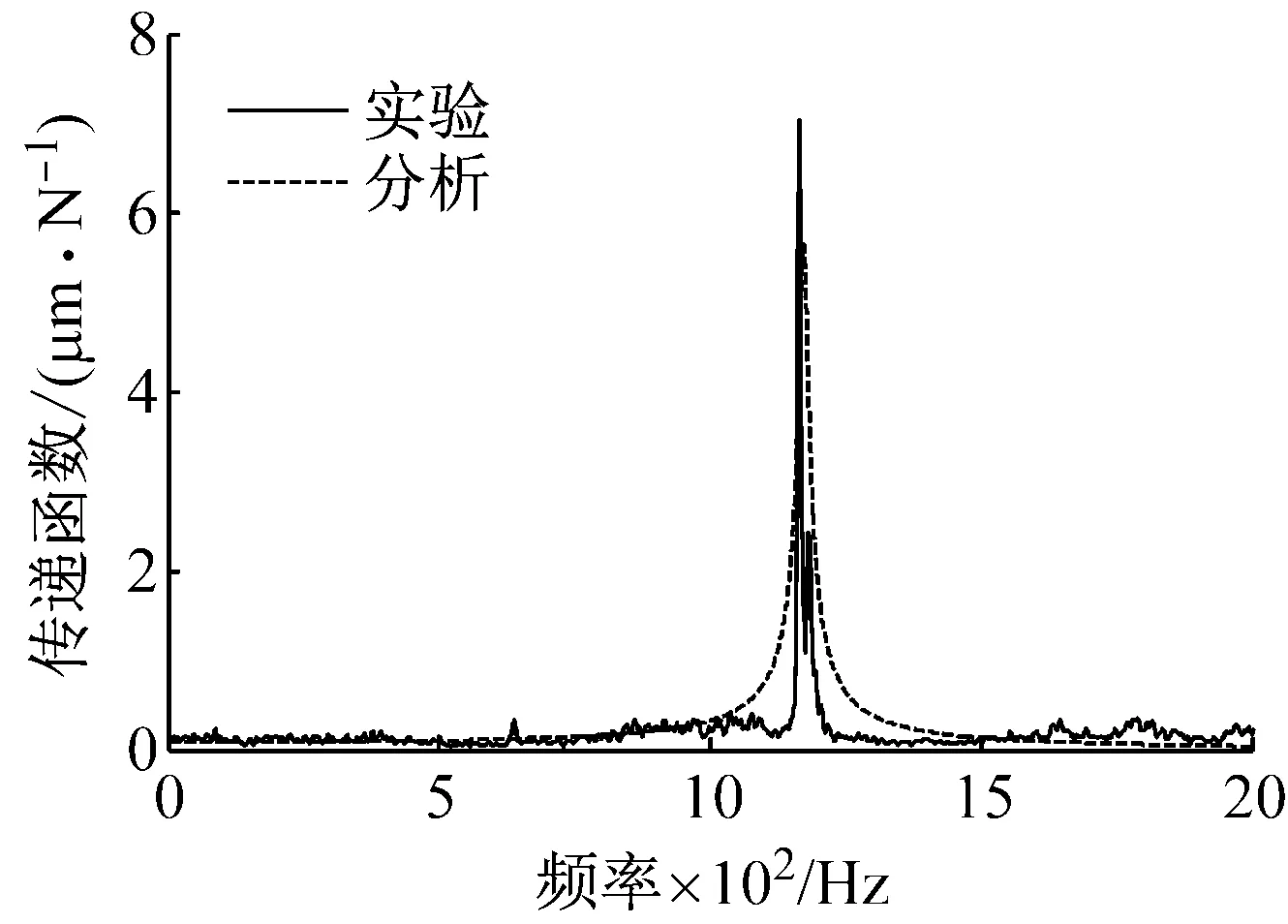
(b) y方向图11 铣刀刀尖点处传递函数Fig.11 Transfer functions at milling cutter
4.4电主轴铣削稳定性能
根据上述高速电主轴铣削稳定性理论,计算系统铣削稳定性瓣图,研究不同转速下的极限切削厚度,分析高速铣削的稳定加工区域,同时完成相应的实验研究。测试加工过程中工件受到的切削力,力传感器型号为Kistler 9251A,灵敏度为8 pC/N。加工过程中进给方向为y方向,进给速度为0.12 m/min,逆铣,被加工材料为铝6061-T6,切削转速分别为10 000 r/min、15 000 r/min和20 000 r/min,切削深度为0.3~2.0 mm,切削厚度为2~10 mm,稳定切削后采集切削力信号的动态值,采样频率为10 000 Hz。
图13表示切削深度为0.3 mm时的铣削稳定瓣图和相应的实验结果。由于铣削深度很小,所以铣削厚度极限值较高,无论考虑转速的影响与否,铣削厚度极限值均在5 mm以上。与未考虑转速影响相比较,考虑转速时,不但稳定瓣图的每个叶瓣底端随着转速的升高逐渐下降,而且存在朝低速方向移动的趋势。图中还标出了不同铣削厚度和不同转速下,铣削过程发生颤振的情况,可以看出,转速为10 000 r/min时,切削厚度为7.0 mm和10.0 mm时发生了颤振,转速为15 000 r/min时,切削厚度为10.0 mm时发生了颤振,转速为20 000 r/min时,各个切削厚度均未发生颤振。考虑转速影响时的分析结果更符合实际情况,转速对电主轴铣削稳定性能的影响不可以忽略。在A点和B点的切削力频谱可以看出,一倍转频和二倍转频处出现了峰值,其原因在前面经讨论过,在此不再做赘述,由于铣刀有三个刀齿,所以峰值在三倍转频处也会出现,为刀齿通过频率。若是以未考虑转速时的系统铣削稳定瓣图进行判定,A点和B点均不会发生颤振,但是根据其切削力频谱可以看出,A点在3 000 Hz附近出现颤振频率,B点未发生颤振,若是根据考虑转速影响时的系统铣削稳定瓣图进行判定,A点正好落在分界线上,将发生颤振,与实验结果相吻合,这说明高转速的作用使得系统铣削稳定性能减弱。
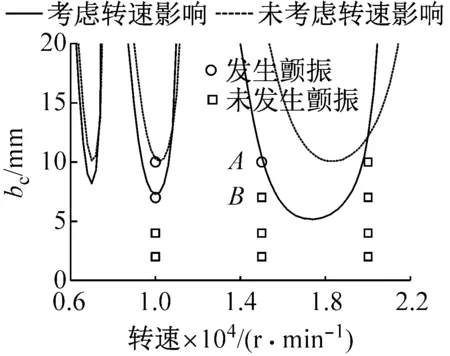
(a) ac=0.3 mm

(b) A点
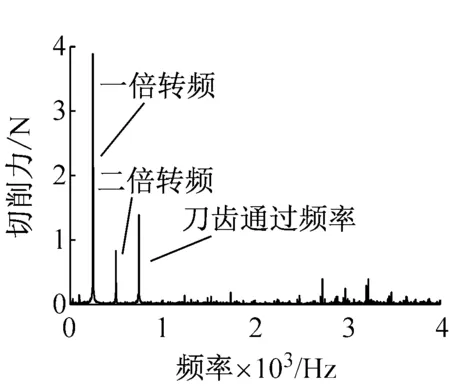
(c) B点图13 切削深度为0.3 mm时的系统铣削稳定瓣图及其实验结果Fig.13 Milling stability lobe diagrams and test results when ac=0.3 mm
图14和图15分别表示切削深度为1.0 mm和2.0 mm时的铣削稳定瓣图和相应的实验结果。均可以看出,考虑转速影响时的系统稳定瓣图的每个叶瓣底端随着转速的升高逐渐下降,并且存在朝低速方向移动的趋势,更加符合实验结果,证明了转速对系统铣削稳定性能有着“弱化”的作用。而且随着切削深度的增大,极限铣削深度不断减小,系统更容易发生颤振。
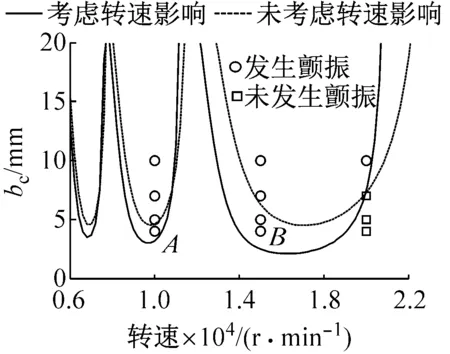
(a) ac=1.0 mm
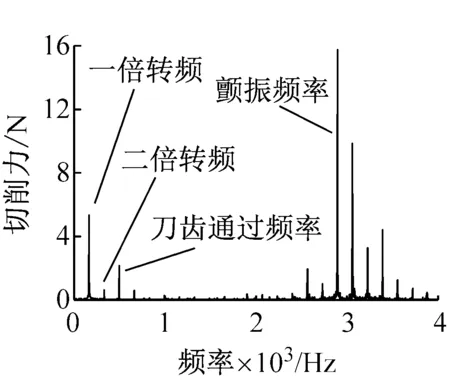
(b) A点
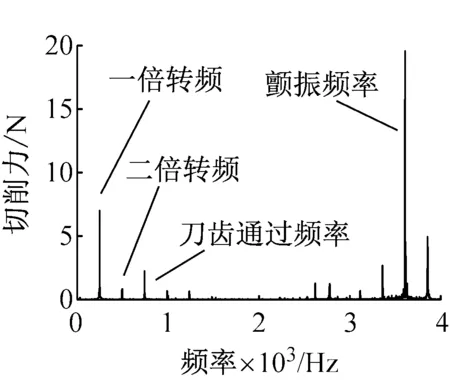
(c) B点图14 切削深度为1.0 mm时的系统铣削稳定瓣图及其实验结果Fig.14 Milling stability lobe diagrams and test results when ac=1.0 mm
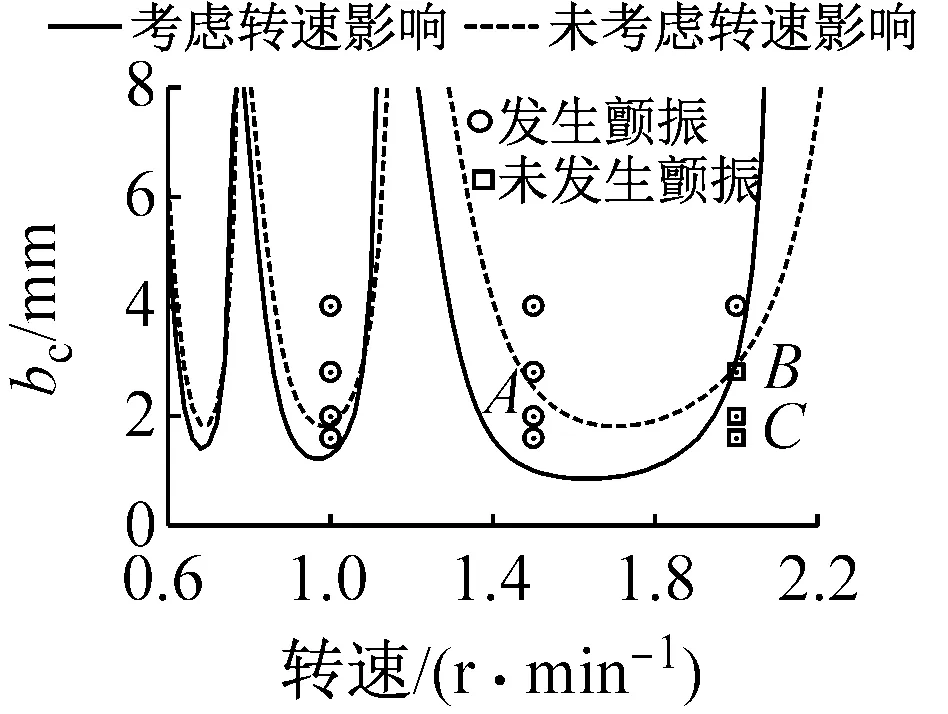
(a) ac=2.0 mm
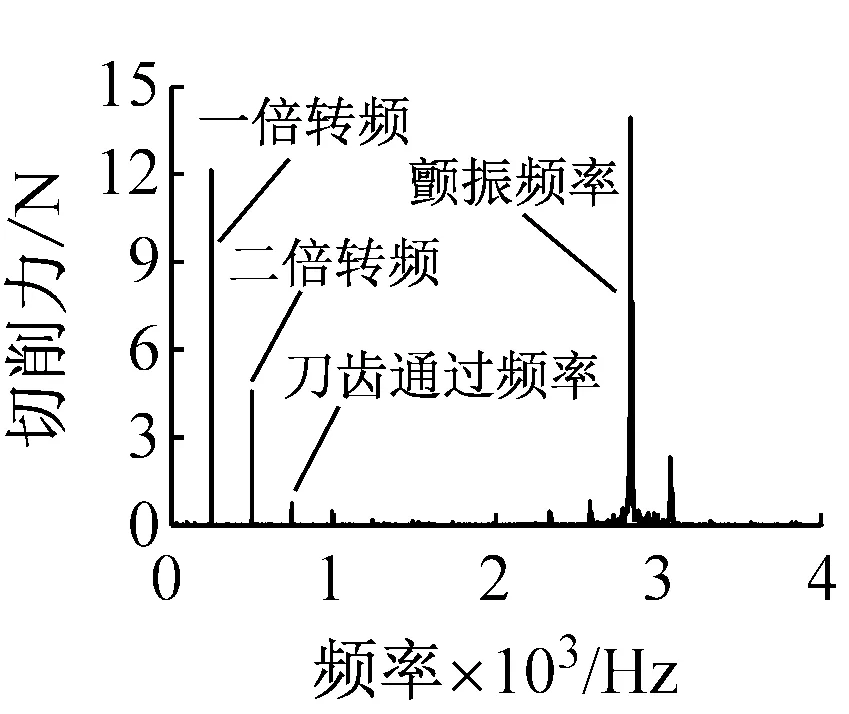
(b) A点
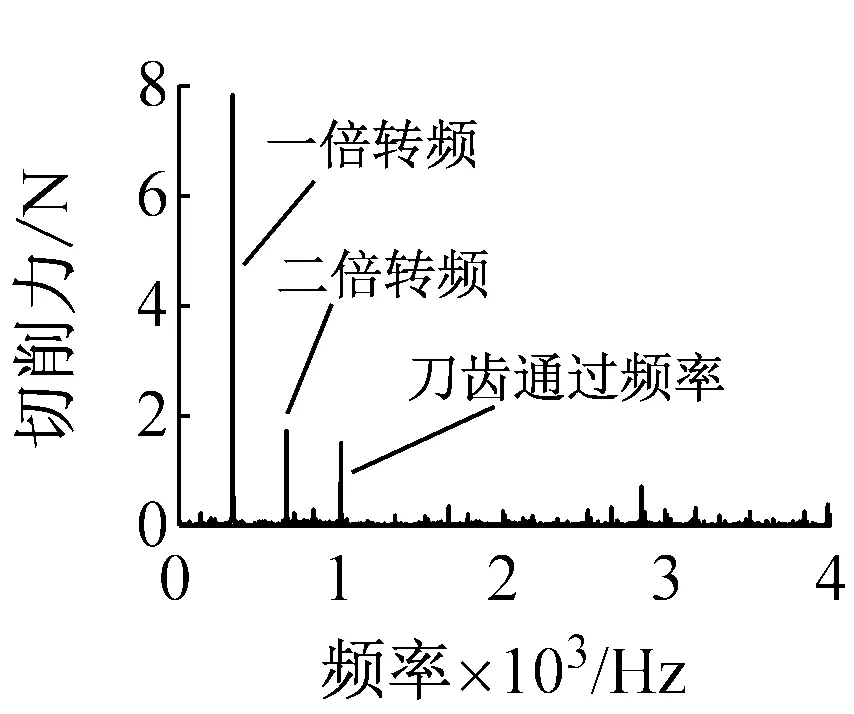
(c) B点
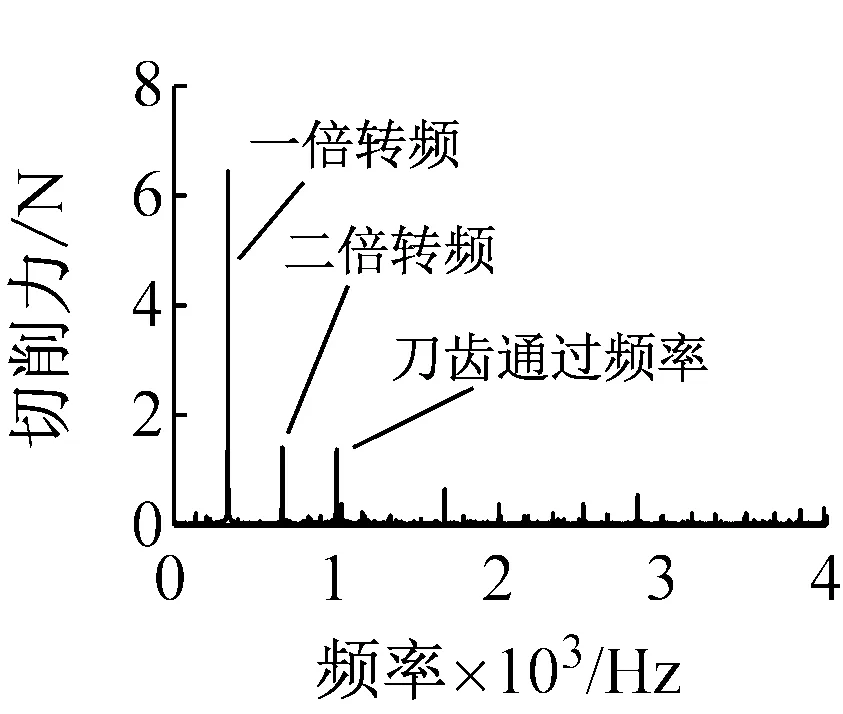
(d) C点图15 切削深度为2.0 mm时的系统铣削稳定瓣图及其实验结果Fig.15 Milling stability lobe diagrams and test results when ac=2.0 mm
5 结 论
通过建立高速电主轴系统铣削稳定性模型,理论分析并且实验验证了D62D24A型电主轴在转速影响下系统动力学特性和铣削稳定性能的若干规律,得出以下结论:
(1) 高速电主轴系统固有特性受到高转速的影响,轴承的“软化”作用使得系统第一阶径向振动固有频率随着转速的升高而降低。
(2) 高转速对系统固有特性的“弱化”作用会反映到刀具刀尖点处的传递函数,从而影响到系统的铣削稳定性能,表现为切削稳定瓣图中稳定区域的减小。
(3) 固有频率的分析结果与实验结果在高转速阶段的误差相对较大,可能存在其他影响系统动力学特性的因素,如温升与热膨胀因素,有待深入研究。
[1] 张伯霖. 高速切削技术及应用[M]. 北京: 机械工业出版社, 2003.
[2] TERMAN T, BOLLINGER J G. Graphical method for finding optimum bearing span for overhung shafts[J]. Journal of Machine Design, 1965, 37(12): 159-162.
[3] SHARAN A M, SANKAR S, SANKAR T S. Dynamic analysis and optimal selection of parameters of a finite element modeled lathe spindle under random cutting forces[J]. Journal of Vibration Acoustics, 1983, 105(4): 467-475.
[4] SHIN Y C. Bearing nonlinearity and stability analysis in high speed machining[J]. Journal of Engineering Industry, 1992, 114(1): 23-30.
[5] WANG K F, SHIN Y C, CHEN C H. On the natural frequencies of high-speed spindles with angular contact bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1991, 205(3): 147-154.
[6] CHEN C H, WANG K W, SHIN Y C. An integrated approach toward the modeling and dynamic analysis of high speed spindles, Part 1: system model[J]. Journal of Vibration and Acoustics, 1994, 116(4): 506-513.
[7] CHEN C H, WANG K W, SHIN Y C. An integrated approach toward the modeling and dynamic analysis of high speed spindles, Part 2: dynamics under moving end load[J]. Journal of Vibration and Acoustics, 1994, 116(4): 514-522.
[8] NELSON H D. A finite rotation shaft element using timoshenko beam theory[J]. Journal of Mechanical Design, 1980, 102(4): 793-803.
[9] LI H Q, SHIN Y C. Integrated dynamic thermo-mechanical modeling of high speed spindles, Part 1: model development[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1): 148-158.
[10] LI H Q, SHIN Y C. Integrated dynamic thermo-mechanical modeling of high speed spindles, Part 2: solution procedure and validations[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1): 159-168.
[11] ENGIN S, ALTINTAS Y. Mechanics and dynamics of general milling cutters, Part 1: helical end mills[J]. International Journal of Machine Tools and Manufacture, 2001, 41(15): 2195-2212.
[12] ALTINTAS Y, BUDAK E. Analytical prediction of stability lobes in milling[J]. Annals of the CIRP, 1995, 44(1): 357-362.
[13] FAASSEN R P H, VAN D W N, OOSTERLING J A J. Prediction of regenerative chatter by modeling and analysis of high-speed milling[J]. International Journal of Machine Tools and Manufacture, 2003, 43(14): 1437-1446.
[14] 梁窨君, 王宁生, 姜澄宇. 薄壁零件高速铣削动态切削力[J]. 南京航空航天大学学报, 2008, 40(1): 89-93.
LIANG Yinjun, WANG Ningsheng, JIANG Chengyu. Dynamic milling force method for high-speed milling of thin-walled parts[J]. Journal of Nanjing University of Aeronautics and Asronautics, 2008, 40(1): 89-93.
[15] 于骏一, 吴博达. 机械加工振动的诊断识别与控制[M]. 北京: 清华大学出版社, 1994.
[16] HAHN R S. On the theory of regenerative chatter in precision grinding operations[J]. Transactions of the ASME, 1954, 76: 593-597.
[17] 蒋宇平,龙新华,孟光.薄壁结构件铣削加工振动稳定性分析[J].振动与冲击,2016,35(2):45-50.
JIANG Yuping,LONG Xinhua,MENG Guang.Stability analysis for thin-walled milling processes[J].Journal of Vibration and Shock,2016,35(2):45-50.
[18] HARRIS T A, KOTZALAS M N. Rolling bearing analysis, Part 2: advanced concepts of bearing technology[M]. 5th ed. Beijing: China Machine Press, 2011.
[19] 李松生. 超高速电主轴球轴承-转子系统动力学性能的研究[D]. 上海: 上海大学, 2006.
[20] HAN S M, BENAROYA H, WEI T. Dynamics of transversely vibrating beams using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.
[21] 王勖成, 邵敏. 有限单元法基本原理和数值方法[M]. 北京: 清华大学出版社, 1995.
[22] GUO D, CHU F, CHEN D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor[J]. Journal of Sound and Vibration, 2002, 254(2): 297-312.
Millingstabilityofhighspeedmotorizedspindles
SHAN Wentao1, CHEN Xiaoan2, WANG Hongchang1, YU Chengtao1
(1. College of Mechanical Engineering,Jiangsu University of Technology, Changzhou 213001, China;2. College of Mechanical Engineering,Chongqing University, Chongqing 400044, China)
A bearing-rotor dynamical model for high speed motorized spindles was established. And the transfer functions at the milling tool were analyzed. On this basis, the milling stability model for motorized spindle systems was proposed. Then, taking the D62D24A type motorized spindle as an example, the weakening effect of the speed on the bearing dynamical stiffness was analyzed, and the first order inherent modal shape and inherent frequency were computed. The milling stability of the system was investigated numerically and experimentally. The milling stability lobe diagrams of the system were analyzed considering the influence of the rotating speed. The theoretical and experimental results describe the trend of milling stability of the system.
high speed motorized spindle; dynamic model; milling stability
TH133
A
10.13465/j.cnki.jvs.2017.19.037
国家自然科学基金青年基金(51405209);江苏省青蓝工程优秀青年骨干教师项目
2016-04-29 修改稿收到日期:2016-08-12
单文桃 男,博士,讲师,1987年生
陈小安 男,博士,教授,1956年生
