基于气动信号分析的风机叶片裂纹故障识别

黎少辉, 蔡利梅

(1.徐州工业职业技术学院 机电工程学院，江苏 徐州 221140；2.中国矿业大学 信息与控制工程学院，江苏 徐州 221116)

基于气动信号分析的风机叶片裂纹故障识别

黎少辉1, 蔡利梅2

(1.徐州工业职业技术学院 机电工程学院，江苏 徐州 221140；2.中国矿业大学 信息与控制工程学院，江苏 徐州 221116)

针对风机叶片裂纹故障，提出通过分析风机出口气动信号，实现在线动态检测裂纹的方法。采集叶片不同状态下的风机出口气动信号，利用db4小波对气动信号进行5层分解，并单支重构，将各频带归一化能量构成6维特征向量；对能量向量进行主成分分析，基于贡献率实现特征选择；采用K均值聚类方法进行叶片状态识别。实验结果表明，气动信号能有效反映风机叶片状态的变化，该方法可以实现叶片正常、异常状态检测及裂纹长度状态区分，提供了风机叶片裂纹在线实时检测依据和手段。

风机叶片裂纹；故障识别；气动信号；小波变换；主成分分析；K均值聚类

叶片是风机的关键部件，工作中承受流体动力、离心力、机械振动、热应力等综合作用。随着风机朝着高速化、重载化发展，叶片的工作条件越来越恶劣，导致叶片容易发生故障。裂纹是叶片常见的故障之一，而叶片断裂引起的事故往往是灾难性的[1]。因此，及早发现叶片裂纹对风机安全运行具有重要意义。目前，各类风机叶片裂纹检测多为停机情况下的静态检测[2-6]，动态的在线检测叶片裂纹方法较少。风机叶片的旋转导致出口气体运动，相应叶片自身结构变化直接影响出口气体的动力学变化[7-11]，这为利用叶片出口气体动力学变化结果诊断叶片结构变化成为可能。找到叶片与气体相互作用的动力学方程是解决该问题的一种捷径，但在实际情况下，很难理清该系统包含哪些状态变量以及这些变量的相互作用规律，即使能够列出动力学方程，使用范围也非常有限。而随时间变化的振动信号时间序列能直接反映相关系统的运动状态，采集分析叶轮出口气动信号成为识别叶片工作状态的思路之一。本文采用小波变换、PCA、K-means等方法分析风机出口气动信号，实现了叶片正常、异常状态检测及裂纹长度状态区分，为风机叶片裂纹在线实时检测提供了依据和手段。

1 风机出口气动信号采集

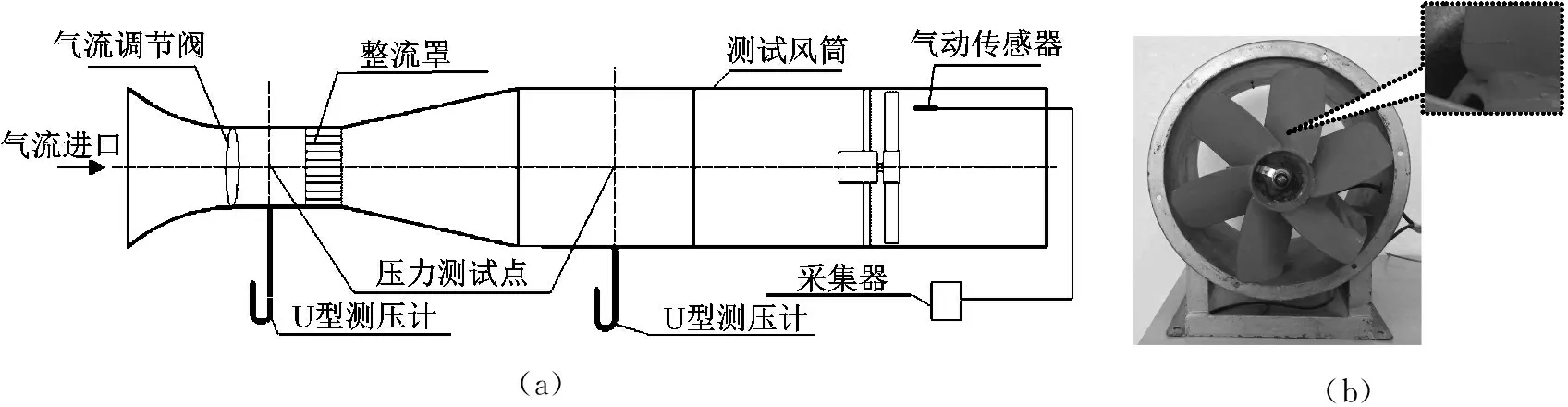
由于风机叶片裂纹实验的难复原性，实验采用了一台小型风机，图1为风机系统及测点布置示意图。

(a)(b)

实验台的设计和风机性能曲线测定按GB 1236—2000《工业通风机-用标准化风道进行性能实验》进行。实验风机的特征参数为：全流量Φ=2 240 m3ph，标准压力为p=120 Pa，转速为n=1 430 r/min，叶宽为55 mm，叶高为136 mm，叶片厚为2.2 mm，材料为碳钢。叶片工作状态为三种：叶片无裂纹、一个叶片根部裂纹15 mm及裂纹延长到20 mm，裂纹采用0.18 mm线电火花加工获得，切缝大约0.2 mm,每种状态均采集五个工况(100%Φ、80%Φ、70%Φ、60%Φ、40%Φ)的出口气动信号,气动传感器放置于叶高80%处沿轴向距离叶片50 mm的位置，重复采集16次。气动传感器采用西安新敏电子科技有限公司生产的CYB11型动态压力传感器，采集信号时，要等到每个工况下风机运行平稳后再采集。

2 基于小波变换的气动信号特征提取

小波变换由于其良好的时频分析特性被广泛地用于多种信号分析。从频域的观点看，信号的能量主要集中在低频部分，高频信号的能量随频率的增加而迅速衰减，所以信号分解时，尽可能的做到高频频带保留长一点，低频部分频段分的密一点。因此，在气动信号分析中，采用了小波变换实现信号分解、重构，并针对重构信号进行特征量计算。

2.1气动信号小波分解与重构

实验中选择db4小波对气动信号进行五层小波分解。气动信号被分解为一个低频带A5和五个高频带D5、D4、D3、D2、D1，然后对分解的各频带进行单支重构。图2为第一次实验中工况1条件下无裂纹、裂纹长15 mm、裂纹长20 mm小波分解后各个单支重构图。

2.2能量特征向量计算及分析

小波分解后的各频带相互独立且无冗余，将单支重构后的信号计算其归一化能量作为识别的叶片状态特征向量。

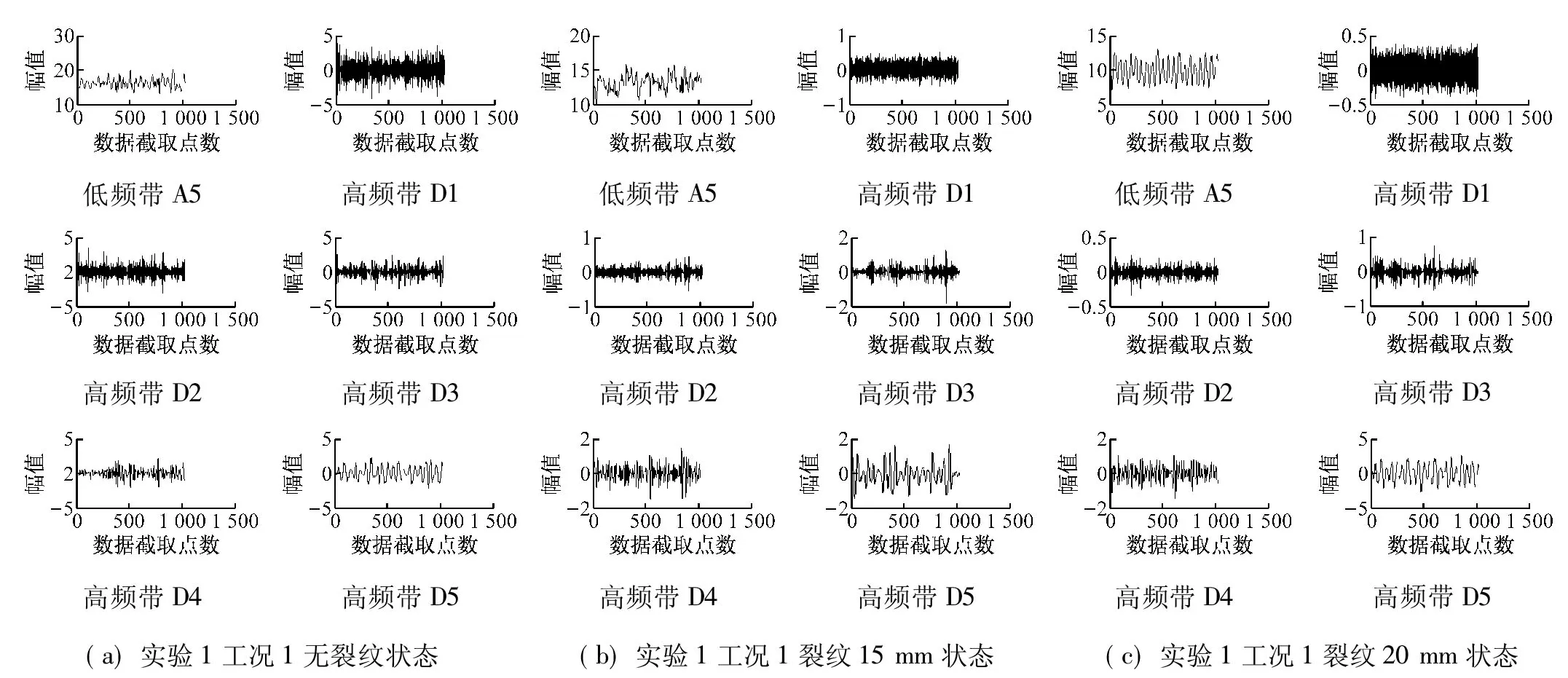
图2 气动信号db4小波分解后各频带重构图
Fig.2 Each frequency band reconstruction of wavelet decomposition

设原始气动信号为f(t)，长度为L，小波变换后单支重构信号为fk(i)，i=1,2,…,L，k=1,2,…,6为分解频带从低到高位置序号，各频带重构信号能量可表示为

(1)

归一化后能量表示为

(2)

从图3中的不同工况气动信号各频带能量变化看出，叶片出现裂纹时，D1、D2、D3、D5较容易分辨出无裂纹与有裂纹频带能量相对变化情况，但不同长度裂纹的频带能量曲线重叠在一起。同时A5、D4频段三种状态能量曲线图出现交织，难以识别，因此有必要对此进一步处理分析。

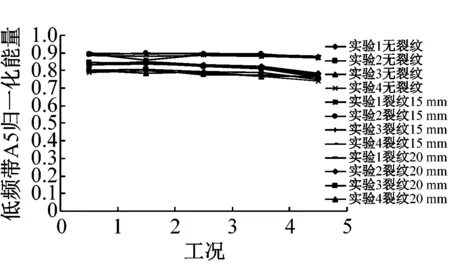
(a) 低频带归一化能量对比

(b) 高频带D1归一化能量对比

(c) 高频带D2归一化能量对比

(d) 高频带D3归一化能量对比

(e) 高频带D4归一化能量对比

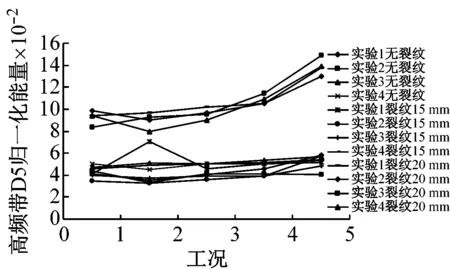
(f) 高频带D5归一化能量对比图3 4次实验无裂纹、裂纹15 mm、裂纹20 mm的小波分解频带重构能量对比图Fig.3 Contrast of energy in different condition

3 基于PCA的特征选择

PCA (Principal Components Analysis)是一种数据分析方法，从一组特征中计算出一组按重要性从大到小排列的新特征，是原有特征的线性组合，相互之间是不相关，达到降低特征维数、在一定程度上消除噪声的目的[12]。

3.1特征矩阵X的构建及PCA变换

将小波变换后提取的特征向量构成N×D维特征矩阵X，如式(3)所示

(3)

式中：xi,j为第i个样本的第j个特征量；N为样本个数；D为原始特征维数。

通过求解最优的正交变换U，按式(4)计算新特征A，使新特征Ai(也称主成分，i=1,2,…,D)的方差达到极值。

A=UTX

(4)

3.2基于贡献率的主成分选择

D个互不相关的主成分包含了原数据中的全部信息，但贡献率(式(5))依次递减，原数据的大部分信息集中在较少的几个主成分上。

(5)

λ为矩阵X的协方差矩阵特征值。选择累积贡献率达到85%以上的前d个主成分作为降维后的新特征，累计贡献率如式(6)所示。

(6)

对原始的六维频带归一化能量特征向量进行PCA变换，所获得的主成分贡献率如表1所示。

表1 各主成分贡献率Tab.1 Principal component contribution rate

第一、二主成分贡献率达99.4%，构成降维后的二维新特征，新特征分布如图4所示。

从图中可看出，经过PCA变换后，无裂纹状态和裂纹状态下的数据点聚集在特征空间的不同区域，裂纹长度变化造成的频带能量变化区分明显；可根据需要将数据分为正常和故障两种情况，或分为正常、不同裂纹长度多种状态。

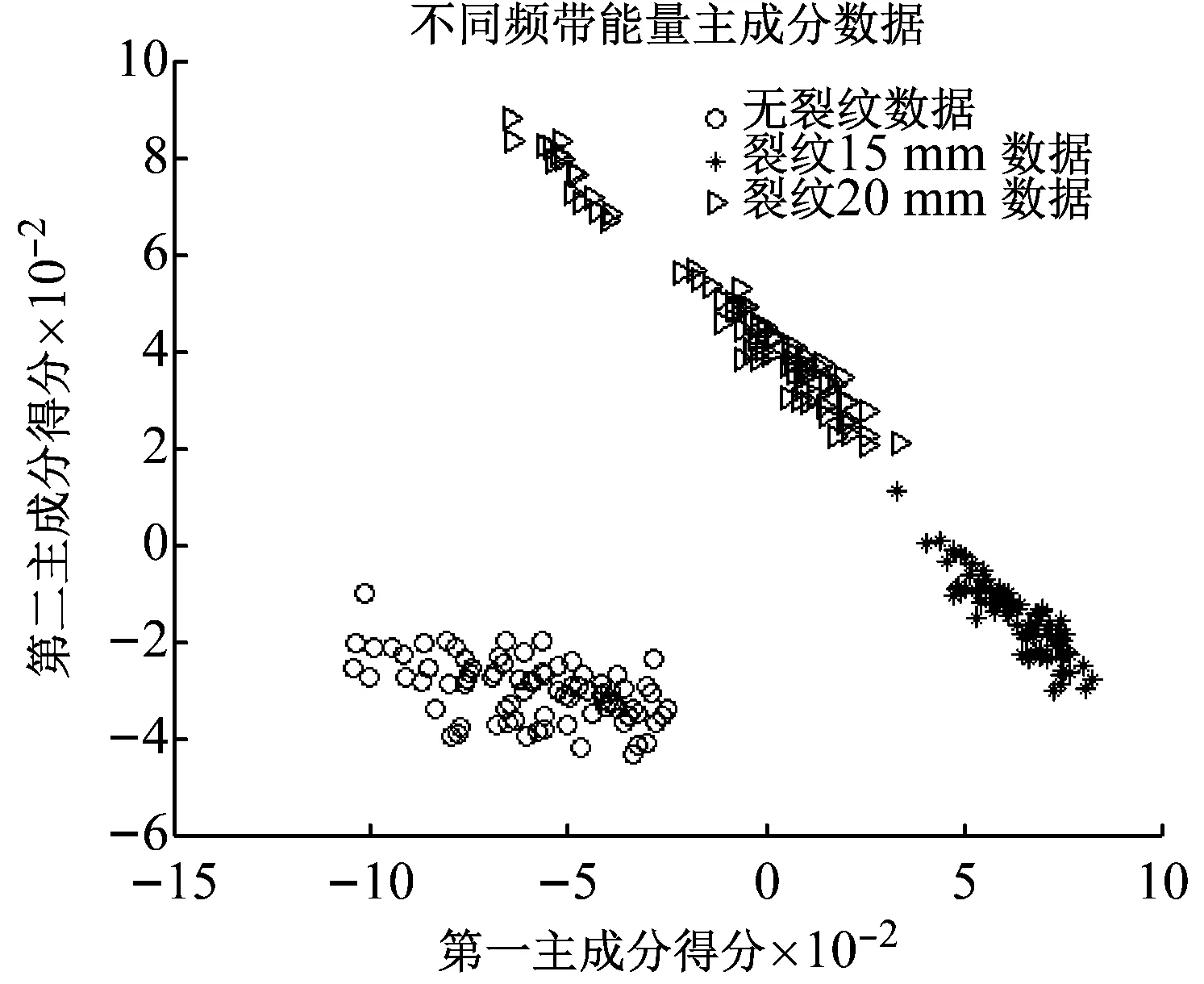
图4 新特征分布图Fig.4 The distribution of new features

4 基于K-Means分析的叶片状态识别

采用K均值算法对PCA降维后的数据进行聚类，聚类结果如图5所示。

(a) 分为有、无裂纹两类

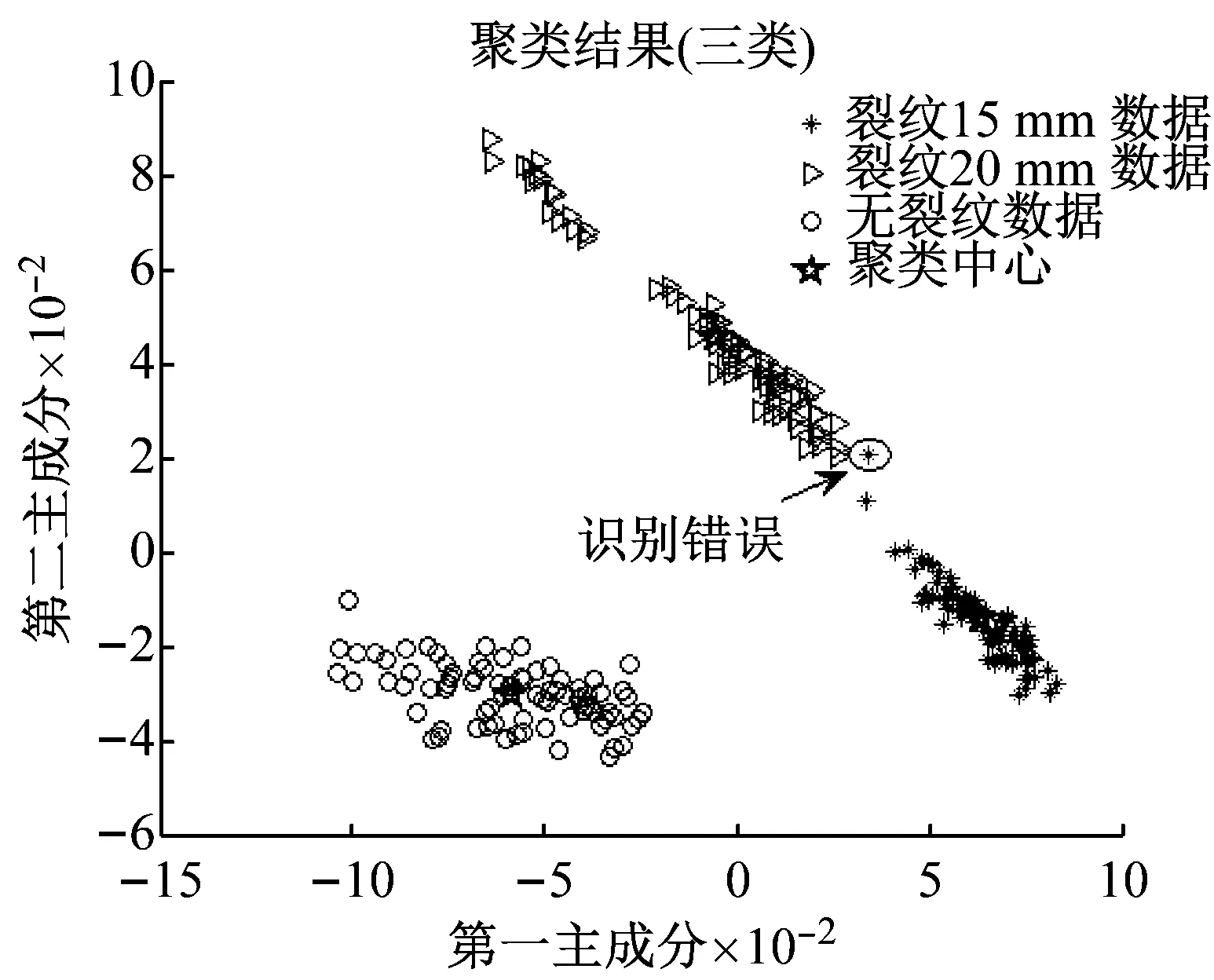
(b) 分为无裂纹、裂纹15 mm、裂纹20 mm三类图5 K-Means聚类结果图Fig.5 K-Means clustering results

图5(a)是无裂纹和有裂纹两类分割的结果，80个正常测试样本无误报，160个有裂纹样本中有16个漏报，总检测率达93.33%，错误率的产生是由于K均值算法以聚类中心做代表点，按照最小距离对样本归类，而裂纹数据呈现细长型分布，裂纹类聚类中心对边缘点控制减弱，导致漏报。

图5(b)是无裂纹、裂纹15 mm、裂纹20 mm三类分割的结果，240个样本中，无误报和漏报，有1个裂纹20 mm的样本被归为裂纹15 mm，总正确率达99.58%。数据如表2所示。

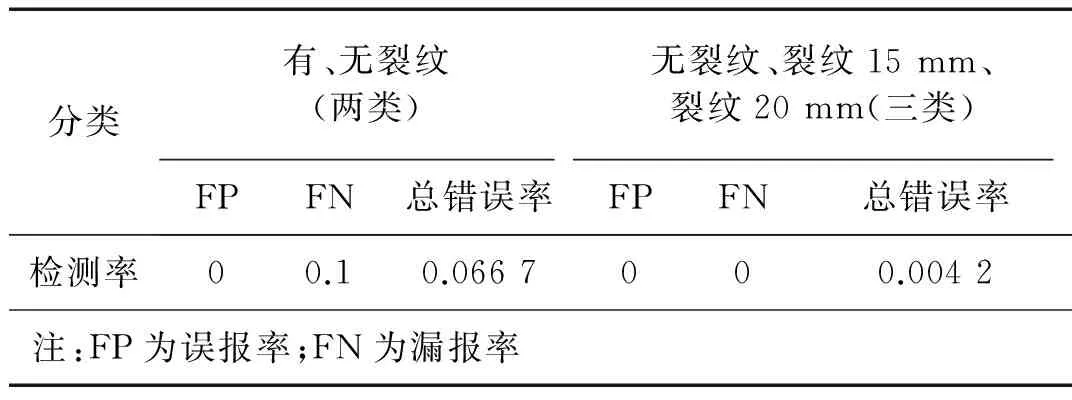
表2 两种聚类识别率Tab.2 Recognition rate

5 结 论

(1) 当叶片出现裂纹时，叶片的固有频率发生变化，该变化在叶轮出口气动信号中有所体现，可以通过气动信号分析实现风机叶片状态在线监测。

(2) 通过对气动信号的小波分解，构建归一化能量特征向量，利用PCA、K-means方法，能够有效实现风机叶片状态识别。

以上分析可以看出，通过采集风机叶轮出口附近气动信号并进行有效分析，能够在线动态监测风机叶片工作状态，且该方法不需要改动风机结构，简单易行，进一步充实了风机在线监测系统功能。

[1] 王艳丰,朱靖,滕光蓉，等.航空发动机转子早期裂纹故障振动特征的维谱分析[J].振动与冲击,2015,34 (1):88-93.

WANG Yanfeng,ZHU Jing,TENG Guangrong,et al.1.5-dimension spectrum analysis on early cracked fault characters of aero engine rotors[J].Journal of Vibration and Shock,2015,34 (1):88-93.

[2] 于霞,张卫民,邱忠超,等.航空发动机涡轮叶片裂纹检测信号特征提取[J].兵工学报,2014,35(8):1267-1274.

YU Xia,ZHANG Weimin,QIU Zhongchao, et al. Signal feature extraction of aero-engine turbine blade crack detection[J].Acta Armamentarii, 2014,35(8):1267-1274．

[3] 董利明,李加,倪辰荫，等. 基于光热调制检测发动机叶片疲劳裂纹的激光声表面波方法[J]. 中国激光,2011,38(11):1103001.

DONG Liming, LI Jia, NI Chenyin, et al. Crack detection of engine blade based on laser-heating assisted surface acoustic waves generated by scanning laser[J]. Chineses Journal of Lasers, 2011,38(11):1103001.

[4] 赵新光,甘晓晔,谷泉，等.基于小波能谱系数的风力机疲劳裂纹特征[J].振动、测试与诊断, 2014,34(2):147-154.

ZHAO Xinguang, GAN Xiaoye, GU Quan, et al. Crack fault feature of wind turbine blade based on wavelet energy spectrum coefficient[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(2):147-154.

[5] 李录平,李芒芒,晋风华，等. 振动检测技术在风力机叶片裂纹故障监测中的应用[J]. 热能动力工程,2013,28(3):207-213.

LI Luping,LI Mangmang,JIN Fenghua，et al. Applications of the vibration detection technologies in monitoring the blade crack fault of wind turbines[J]. Journal of Engineering for Thermal Energy and Power, 2013,28(3):207-213.

[6] 周勃,谷艳玲,项宏伟,等.风力机叶片裂纹扩展预测与疲劳损伤评价[J].太阳能学报, 2015,36(1):41-48.

ZHOU Bo, GU Yanling, XIANG Hongwei, et al. Crack growth prediction and fatigue damageevaluation on wind turbine bladeacta energiae[J]. Solaris Sinica,2015,36(1):41-48.

[7] 张俊红,杨硕,刘海,等. 裂纹参数对航空发动机叶片频率转向特性影响研究[J]. 振动与冲击,2014, 33(20):7-11.

ZHANG Junhong,YANG Shuo,LIU Hai,et al. Influence of crack parameters on frequency veering characteristic of aero-engine blade[J].Journal of Vibration and Shock,2014,33(20):7-11.

[8] JUNG C, SAITO A, EPUREAN B I. Detection of cracks in mistuned bladed disks using reduced-order models and vibration data[J]. Journal of Vibration and Acoustics, 2012, 134(12):061010.

[9] SAITO A, CASTANIER M P, PIERRE C. Effects of a cracked blade on mistuned turbine engine rotor vibration[J]. Journal of Vibration and Acoustics, 2009, 131(6): 061006.

[10] KHANAM S, DUTT J K, TANDON N. Extracting rolling element bearing faults from noisy vibration signal using kalman filter[J]. Journal of Vibration and Acoustics, 2014, 136(6):031008.

[11] CHIU Y J, HUANG S C. The influence of a cracked blade on rotor’s free vibration[J]. Journal of Vibration and Acoustics, 2008, 130(5): 054502.

[12] 古莹奎,承姿辛,朱繁泷. 基于主成分分析和支持向量机的滚动轴承故障特征融合分析[J]. 中国机械工程,2015,28(20):2778-2787.

GU Yingkui, CHENG Zixin, ZHU Fanlong. Rolling bearing fault feature fusion based on PCA and SVM[J]. China Mechanical Engineering, 2015,28(20):2778-2787.

Fanbladecrackfaultdiagnosisbasedontheanalysisofpneumaticsignals

LI Shaohui1, CAI Limei2

(1. School of Mechanical and Electrical Engineering,Xuzhou College of Industrial Technology, Xuzhou 221140, China; 2. School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116, China)

Based on the analysis of pneumatic signals obtained at fan outlet，a method for the dynamic detection of cracks in fan blades was proposed. The original pneumatic signals were collected under different conditions of the fan; and then decomposed and reconstructed by using the multi-resolution wavelet transform. The normalized energy in every frequency band was applied to composea six dimension characteristic vector. The principal components analysis (PCA) was used for the dimension reduction and feature selection. At last, the K-means clustering method was adopted to recognize the condition of the fan blades. The results show that pneumatic signals can reflect effectively the state change of fan blades; and the method can make a distinction between the normal and abnormal states of fan blades efficiently. It provides the foundation and method for the on-line inspection of fan blade cracks.

fan blade crack; fault diagnosis; pneumatic signal; wavelet transform; principal components analysis; K-means

TH165.3

A

10.13465/j.cnki.jvs.2017.19.034

江苏省“青蓝工程”资助项目；江苏省高职院校高级访问学者计划项目

2016-01-08 修改稿收到日期：2016-08-01

黎少辉 男，博士，副教授，1974年9月生

蔡利梅 女，博士，副教授，1977年2月生