基于EMD与相关系数原理的故障声发射信号降噪研究
2017-11-06刘东瀛邓艾东刘振元黄宏伟
刘东瀛, 邓艾东, 刘振元, 李 晶, 张 瑞, 黄宏伟
(1. 东南大学 火电机组振动国家工程研究中心,南京 210096;2. 宁波市自来水有限公司,浙江 宁波 315041;3. 东南大学 信息科学与工程学院,南京 210096;4. 国电投河南电力有限公司技术信息中心,郑州 450001)
基于EMD与相关系数原理的故障声发射信号降噪研究
刘东瀛1, 邓艾东1, 刘振元2, 李 晶3, 张 瑞1, 黄宏伟4
(1. 东南大学 火电机组振动国家工程研究中心,南京 210096;2. 宁波市自来水有限公司,浙江 宁波 315041;3. 东南大学 信息科学与工程学院,南京 210096;4. 国电投河南电力有限公司技术信息中心,郑州 450001)
声发射信号经常受到许多非平稳非线性噪声的干扰,这给对有用声发射信号的识别增加了困难。依据相关系数原理提出了一种基于经验模态分解的旋转机械碰摩声发射信号的去噪方法,通过求出含噪信号经过经验模态分解后所得到的各阶本征模态函数与含噪信号自身的相关系数,根据其变化规律并结合经验模态分解的滤波特性,选取被噪声污染程度较低的本征模态函数对信号重构以达到去噪目的。该方法应用于被不同种类噪声污染的碰摩声发射信号的去噪,实验结果表明此方法能有效的去除噪声,并具有不受主观参数影响,结果稳定,自适应等优点。
碰摩;声发射;信号降噪;经验模态分解;相关系数
声发射(Acoustic Emission,AE)信号以其响应灵敏,频带范围宽,频率成分丰富在旋转机械早期碰摩故障检测中具有独特的优势[1-2]。但在旋转机械碰摩AE信号检测中,AE信号经常会受到实际噪声的干扰,甚至被湮没,使得对有用的碰摩AE信号的识别变得困难,所以在分析采集到的AE信号时,必须要对其降噪处理。Norbert Wiener提出的维纳滤波理论是从噪声中提取原始信号的最基本方法,但这要求提前获得期望信号和噪声的相关函数,才能由维纳霍夫方程求解得到滤波器的最优解,且其主要适用于平稳信号,所以应用范围受到限制。Donoho[3]提出了小波阈值法降噪。基于小波(包)阈值降噪在对非平稳信号降噪效果上优于传统方法[4],但其存在小波分解层次、小波基、阈值函数及阈值选取等问题。同时,碰摩AE信号自身表现出的非线性和非平稳特征,给许多信号处理方法带来了局限性。
经验模态分解(Empirical Mode Decomposition,EMD)是由Huang等[5]于1998年提出的一种新型自适应信号时频处理方法,特别适用于非线性非平稳信号的处理。其最大的优点是依据信号自身的时间尺度特征进行分解,无需预先设定基函数,克服了小波变换时选择基函数的困难。它使复杂信号分解成有限个本征模态函数(Intrinsic Mode Function,IMF)和余项,各阶IMF在不同的时间尺度上体现了原始信号的局部特征[6],对各阶IMF进行频谱分析,可知由低阶IMF至高阶IMF的频率由高到低变化,故可利用此性质对含噪信号进行降噪处理。
谭善文等[7]定性分析了Hilbert-Huang变换在时空滤波的实现过程,并将其方法应用于机床主轴振动信号的处理,与Fourier变换和小波变换做了比较,证明了Hilbert-Huang变换滤波的有效性。陈隽等[8]运用集合经验模态分解方法对疲劳信号进行了降噪处理,采取除去前若干阶IMF和余项,重构余下的IMF得到降噪后的信号,但并未具体说明取舍IMF的方法。Boudraa等[9]提出了基于连续均方误差准则去噪的方法,即找到IMF能量全局极小值的位置作为噪声主导分量与信号主导分量的分界点,取从其后一阶开始重构。孙伟峰等[10]对其方法提出了改进,即若在全局极小值点之前出现局部极小值点,则重构从之前的局部极小值点开始,并用仿真信号证明了有效性。但当信噪比较高时,IMF能量的第一个极小值点会出现在高阶IMF处,如果此时选择只对其后面的IMF重构,会漏掉很多有用信息,出现输出信噪比下降的情况。王婷[11]在第5章第4节提出了一种基于自相关函数特性的EMD去噪算法,利用理想高斯白噪声的归一化自相关函数在零点处为1,其余点处为0的特点,通过对分解得到的各阶IMF做自相关函数图形判定各阶IMF中所含噪声比重,舍弃噪声比重大的低阶IMF分量,对剩余的高阶分量重构,达到去噪目的。但此种方法只能根据图形波动大小对IMF进行取舍,没用具体的阈值来划分,会出现误差,且当所加入噪声为诸如自相关函数图形在非零点处波动较大的粉红噪声时,此方法失效。并且,上述文章都只以白噪声作为噪声源,并未考虑其他噪声。
本文以旋转机械碰摩AE信号为研究对象,在无噪声污染的碰摩AE信号中分别加入了白噪声和粉红噪声,利用含噪信号经EMD分解后的各阶IMF与含噪信号的相关系数作为筛选IMF的依据,实验结果证明了此方法的有效性。
1 EMD方法
EMD通常被称为是一个“筛选”过程。这个筛选过程依据信号特点自适应地把任意一个复杂信号分解为一系列IMF,每个IMF都应满足[12]:① 在一完整的数据段内,极值点和过零点的数目必须相同或至多相差1;② 无论信号处于哪一时刻,由其局部极大值构成的上包络和局部极小值构成的下包络的平均值为0。
具体步骤可按如下分解:
步骤1确定信号x(t)的所有局部极大值点和极小值点,利用三次样条曲线分别连接所有局部极大值点和局部极小值点形成上包络与下包络。
步骤2计算出上下包络线的均值,记为m1
x(t)-m1=h1
(1)
理想的,如果h1满足IMF的两个条件,则h1即为x(t)的一个IMF。
步骤3如若h1不是x(t)的一个IMF,则把h1作为原始信号,重复步骤1得到上下包络线的新的均值m11
h1-m11=h11
(2)
判断h11是否满足IMF条件,如还不满足,则再重新循环k次,有
h1k-1-m1k=h1k
(3)
使得h1k满足IMF条件,令c1=h1k,c1即为信号x(t)的第一个IMF。
步骤4将得到的c1从x(t)中分离出来,有
r1(t)=x(t)-c1(t)
(4)
把r1(t)作为原始信号,重复步骤1~步骤3可得到信号的第二个IMF:c2。往复循环n次,就可得到属于x(t)的n个IMF,同时
(5)
当rn(t)成为一个单调函数不能再分解时,式(5)的循环结束,由此得到
(6)
式中:ci(t)为x(t)的第i个IMF;rn(t)为x(t)分解后的残余分量。
2 基于相关系数原理的EMD去噪
2.1基于相关系数原理的EMD去白噪声方法
本文用相关系数ρ反映含噪信号x(t)与各阶IMF之间相关关系的密切程度。
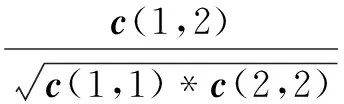
(7)
式中:c为矩阵[x,IMF]的协方差矩阵;N为信号的采样点数。
由于各阶IMF是由x(t)分解得到的,在多数情况下应有0<ρ<1。但实验发现,当含噪信号x(t)的信噪比较大时,会出现其分解得到的某高阶IMF与自身的相关系数小于0的情况。由于欲通过相关系数反应各阶IMF中碰摩AE信号能量与噪声能量的相对变化趋势,故当相关系数为负数时,对其取绝对值即可。
通过分析各阶IMF与x(t)的ρ,结合EMD方法与噪声自身的特点,通过筛选重构IMF达到去噪目的。
白噪声是功率谱密度在整个频域内均匀分布的噪声,当用EMD方法将混有白噪声的信号分解为n阶IMF时,低阶IMF分量会将大于碰摩AE信号频率的白噪声滤掉,与碰摩AE信号频率相重合的白噪声在前几阶分解时会得到明显的减弱,直至分解至第k(k>1)阶时,前(k-1)阶IMF会将大于碰摩AE信号频率部分的噪声几乎全部滤掉,且使与碰摩AE信号频率部分重合的低频噪声大幅度衰减。
k值的大小可根据各阶IMF与含噪信号x(t)的相关系数确定:
(1) 当含噪信号x(t)的信噪比很大时,x(t)经EMD处理后得到的第一阶IMF就可将绝大部分噪声滤掉,此时,第一阶IMF与x(t)的相关系数ρ1很小,第二阶IMF与x(t)的相关系数ρ2会陡增,这时从第二阶IMF开始重构,就可得到去噪后的信号s(t)。
(2) 当x(t)的信噪比不是很大时,第一阶IMF~第(k-1)阶IMF与x(t)的相关系数单调递减,直至第k阶时增大,即在第(k-1)阶处产生了极小值。这说明在前(k-1)阶IMF中,噪声能量大于碰摩AE信号能量,并随着IMF阶数的增加,所含噪声能量不断减小,直至第(k-1)阶时降至最低,但此时噪声能量仍大于碰摩AE信号能量。从第k阶IMF开始,相比于噪声,碰摩AE信号的能量开始加大,此时从第k阶开始重构,即可得到去噪后的信号s(t)
(8)
2.2基于相关系数原理的EMD去粉红噪声方法
粉红噪声也是自然界最常见噪声之一,与白噪声不同的是它的频率分量功率主要分布在中低频段。如果按照前述方法去除粉红噪声,较之白噪声其降噪效果大为降低。为了提高粉红噪声的降噪效果,对前述方法改进如下:
用处理白噪声信号相同的方法,找到加入粉红噪声的碰摩AE信号x(t)经EMD处理后的第k阶IMF,其与x(t)的相关系数ρk会增大,表明前(k-1)阶IMF已把绝大部分超出碰摩AE信号自身频率范围的高频粉红噪声滤掉,与碰摩AE信号频率重合的中低频噪声也有所减弱。ρk相对于ρk-1有所增加,表明在第k阶IMF中,碰摩AE信号的能量已经超过了噪声能量。但经实验数据表明,ρk-ρk-1<0.05,这说明这两阶IMF与x(t)的相关性几乎相同,所以可近似认为在第k阶IMF中,噪声能量与碰摩AE信号能量相同。而ρk+1相对于ρk的增加程度会明显大于ρk相对于ρk-1的增加程度,说明在第(k+1)阶IMF中,碰摩AE信号的能量已经明显大于噪声能量了。之所以会出现这种情况,正是由于粉红噪声的频率分量功率主要分布在中低频段,使得第k阶IMF中的噪声能量高于第(k-1)阶IMF的噪声能量,在一定程度上掩盖了本应以中低频段为主的碰摩AE信号能量。在第(k+1)阶IMF中,虽然噪声能量又进一步得到增加,但此时碰摩AE信号的能量已经成为了主导部分,所以选择舍弃第k阶IMF,从第(k+1)阶开始重构。这虽然意味着丢弃了第k阶中的部分有用信息,但相比于保留此阶,丢弃的噪声能量也有所增加,从整体上看有利于信号的降噪。
从第k阶IMF~第m阶IMF,各阶IMF与x(t)的相关系数逐渐增大至极大值(也是最大值)处,再至第w阶达到局部极小值点。在第k阶~第w阶IMF中,虽然噪声能量一直增加,但还是弱于碰摩AE信号的自身能量,在第w阶达到临界点。从第(w+1)阶开始,噪声能量已超过了碰摩AE信号的能量,故而舍去。最后得到去噪后的信号s(t)
(9)
2.3基于相关系数原理的EMD去两种噪声的方法对比
白噪声与粉红噪声不同的频率分量功率分布决定了需用不同的方法对含噪信号的IMF进行筛选重构,以达到最好的去噪效果。
因为白噪声的功率谱密度随频率的分布均匀,其能量不会随IMF阶数的增加而变化,所以不会出现第(k+1)阶IMF中的碰摩AE信号能量被噪声能量所掩盖的情形。同时,虽然用EMD处理后的含白噪声信号的IMF与自身的相关系数也会存在第二个极小值——w阶处,但此时第w阶及其之后的IMF与带噪信号的相关系数已变得很小,说明在IMF中碰摩AE信号能量与噪声能量都变得很低,噪声的影响几乎可以忽略。同时为了采集到高阶IMF中碰摩AE信号的细节信息以使信号的恢复效果达到最佳,本文在此重构了第k阶~最后一阶IMF。
3 实验分析
3.1碰摩AE信号的获取
本文碰摩实验系统由转子碰摩实验台,盖状导波板,调速器和声发射采集系统组成。如图1和图2所示,转子碰摩试验台是由3个具有滑动轴承的轴承座,两个碰摩圆盘,碰摩螺钉组成。碰摩圆盘直径75 mm,厚25 mm。碰摩螺钉通过盖状导波板上螺孔指向转轴中心,并与圆盘侧面接触。当转子以一定的转速旋转时,碰摩螺钉就会与碰摩圆盘发生碰摩。碰摩产生的AE信号经由导波板被声发射传感器所接收。为了降低由于介质不连续而引起的AE波形畸变,在接触面之间填充耦合剂。导波板上有2个螺孔,可以模拟螺钉与2个碰摩圆盘在2个位置处产生的碰摩,孔间距离严格保持与碰摩圆盘之间距离一致。本实验就一处位置通过调节螺钉实现螺钉与圆盘之间的碰摩。
AE信号采集系统由内置PCI-2声发射采集卡的工控机、UT-1000宽频AE传感器及前置放大器组成。PCI-2声发射采集卡具有18位A/D分辨率,设置AE信号采样频率为1.024×106bit/s,滤波器频带为20~200 kHz,AE放大器增益为40 dB,采集时间21.483 ms。由于绝大多数机械噪声的频率范围最多只能达到几十千赫兹,在高频段受环境噪声影响小,因此选择谐振频率为100 kHz以上的传感器能有效克服机械干扰噪声影响[13]。为降低Lamb波和边界反射波的混叠,实验采集碰摩初期信号。

图1 实验台内部仿真图Fig.1 The experimental facility internal simulation picture

图2 实验台实物图Fig.2 The experimental facility photograph
3.2实验结果分析
图3是在上述实验条件下采集到的较为纯净的碰摩AE信号,数据点取为3 000点,分别向其中加入不同输入信噪比(Signal Noise Ratio, SNRin)的白噪声和粉红噪声(噪声源由英国TNO感知学会所属的荷兰RSRE研究中心提供),采用输出信噪比(SNRout)、均方误差(Mean Squared Error, MSE)及去噪后信号的波形作为衡量EMD方法去噪有效性的标准。其中SNRin、SNRout与MSE定义为
式中:σy为原始碰摩AE信号y(t)的标准差;σz为添加的噪声z(t)的标准差;σz′为滤出的噪声z′(t)的标准差;N为采样点数。
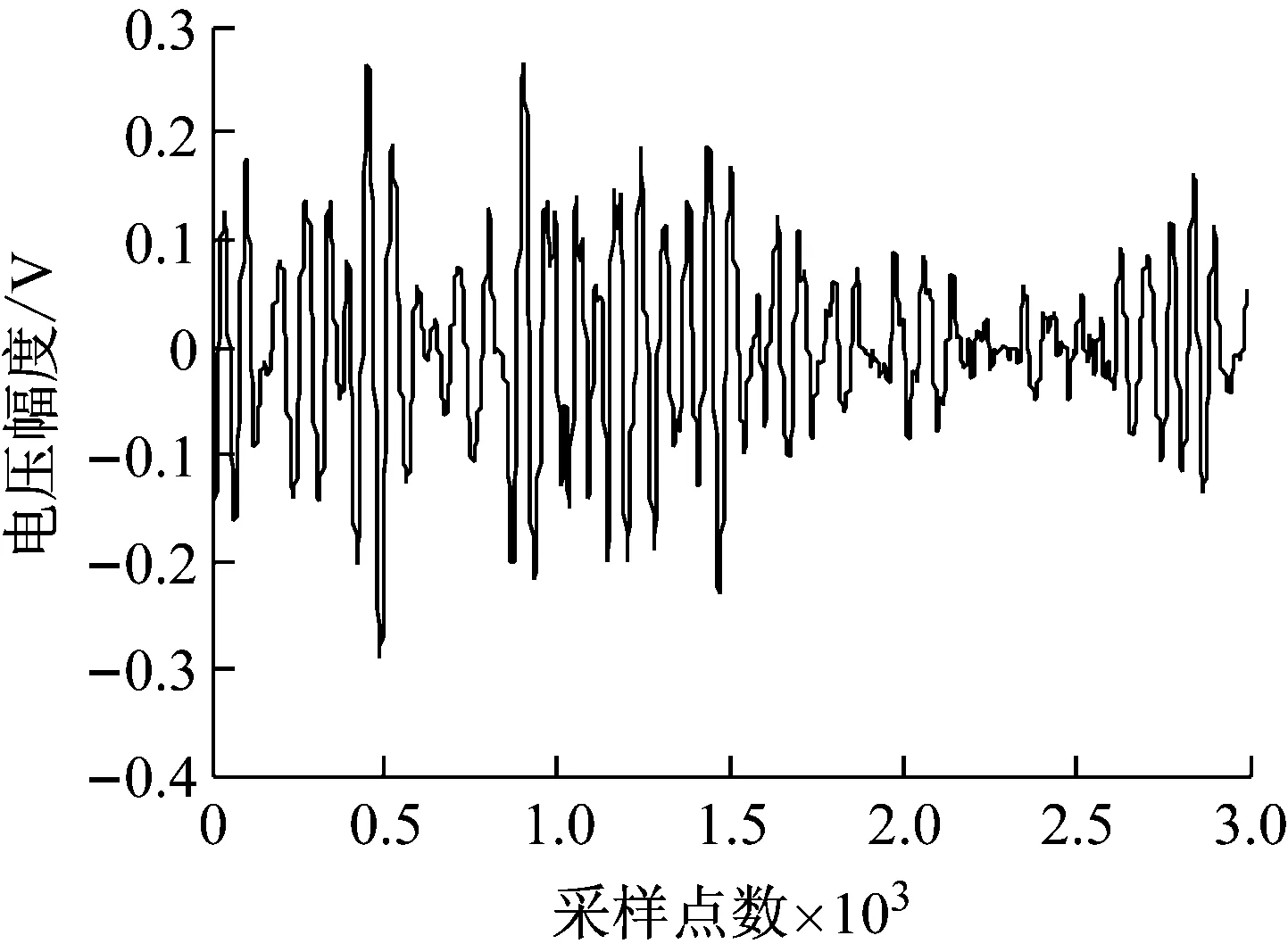
图3 纯净碰摩AE信号Fig.3 Pure rub-impact AE signal
表1为含白噪声AE信号经EMD处理后的情况。

表1 含白噪声信号经EMD后的情况Tab.1 The signal condition with white noise after EMD
由表1可看出含白噪声AE信号依据自身的时间特征尺度分解出的IMF个数及其IMF的重构阶数。随着SNRin的增加,重构起始阶呈降低趋势,即只需要较少数目的IMF即可滤掉大部分白噪声。
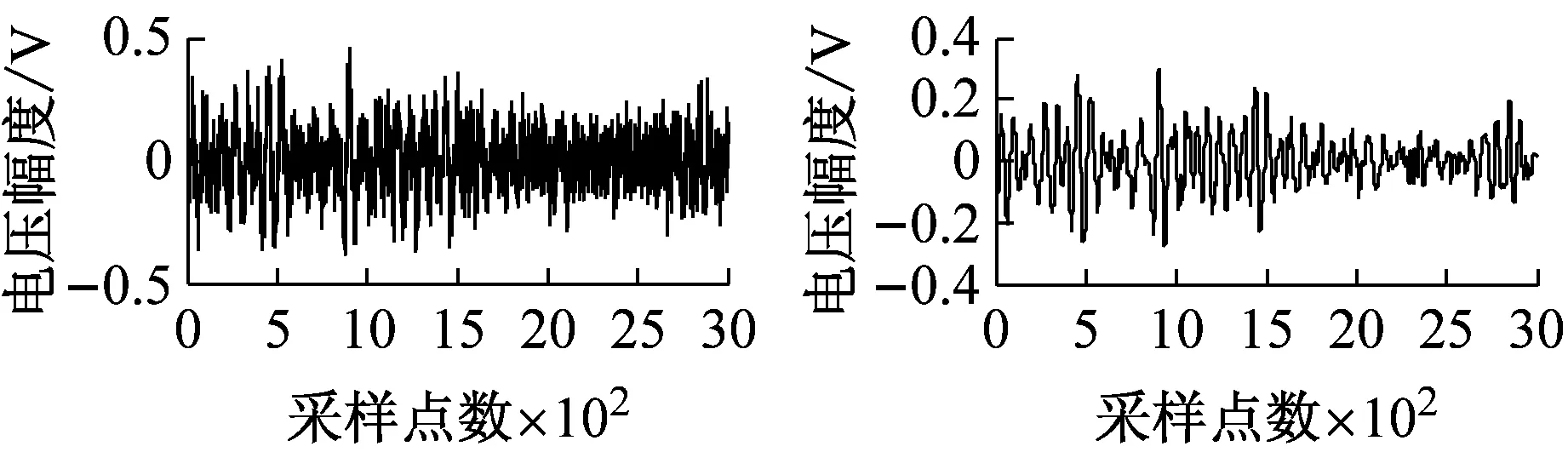
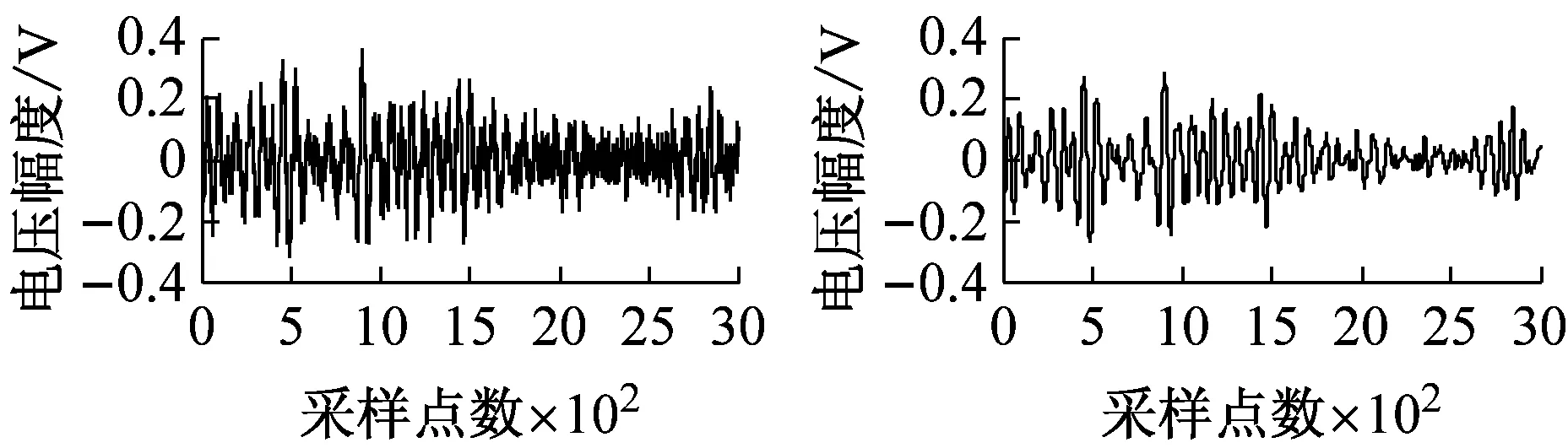
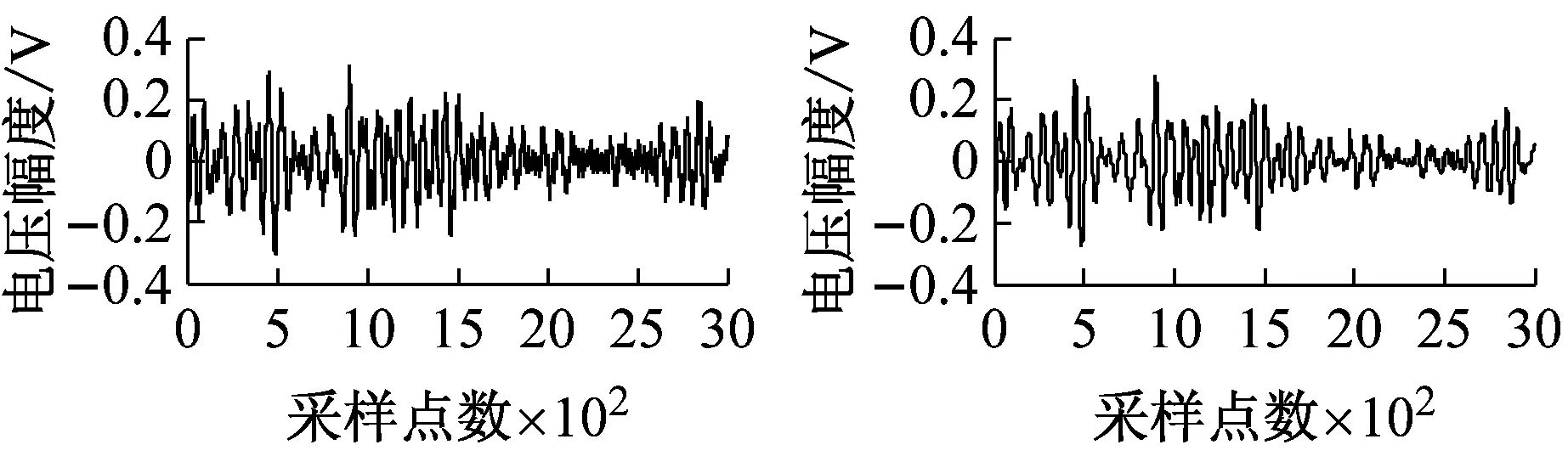
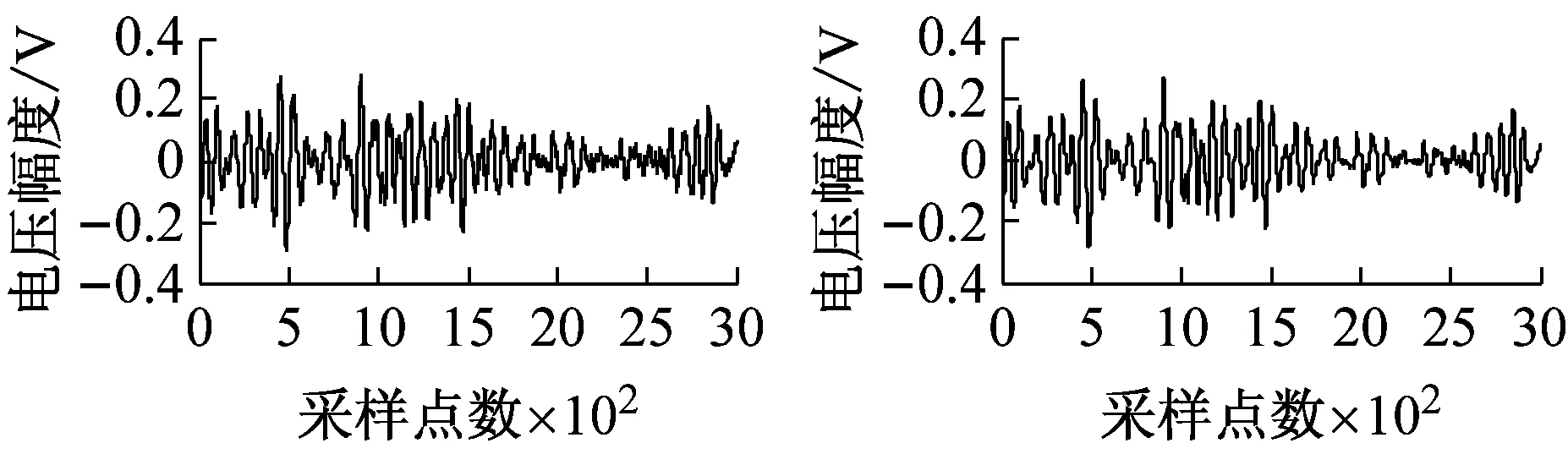
图4为加入不同信噪比白噪声时降噪前后的碰摩AE波形图。
由波形图知,当SNRin≤0 dB时,该方法可使完全湮没在噪声中的碰摩AE信号大致还原出来。当SNRin≥18 dB时,加噪信号会越来越接近原始碰摩AE信号。此时,该方法仍可起到不错的降噪效果,在细节处去噪,使加噪信号接近原始碰摩AE信号。
表2为含粉红噪声信号经EMD处理后的情况。
图5为加入不同信噪比粉红噪声时降噪前后的碰摩AE波形图。
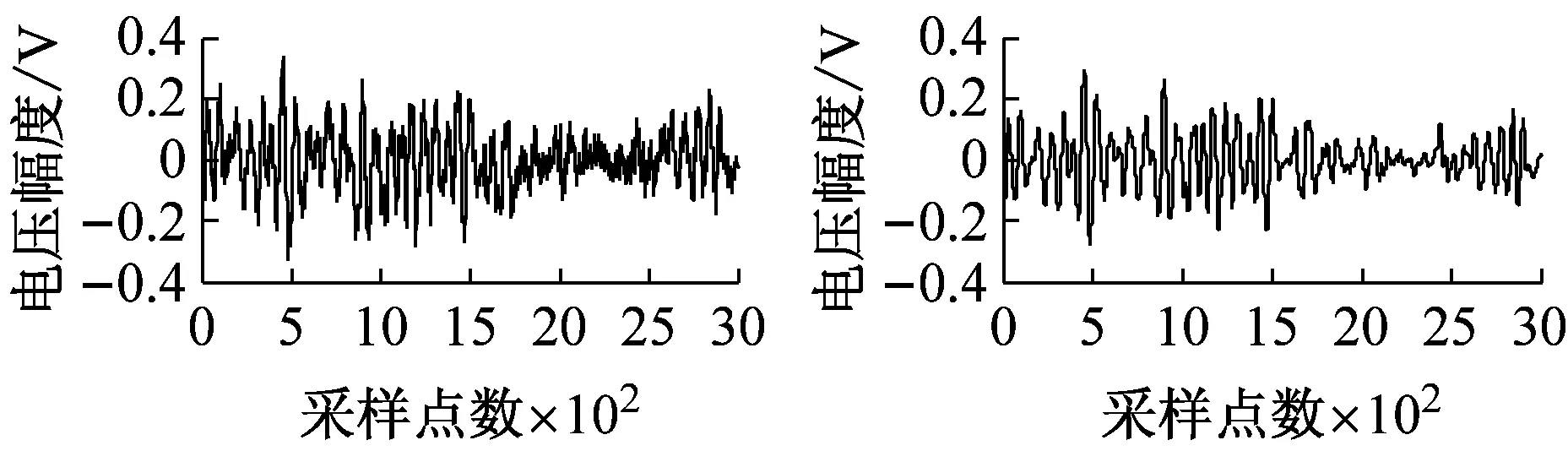
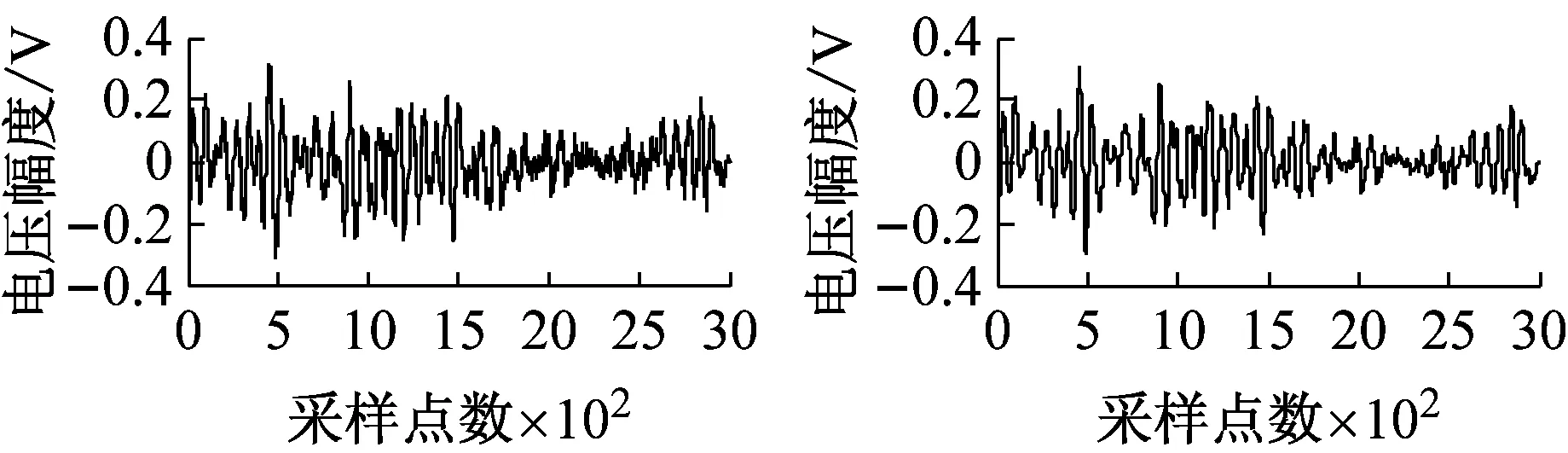
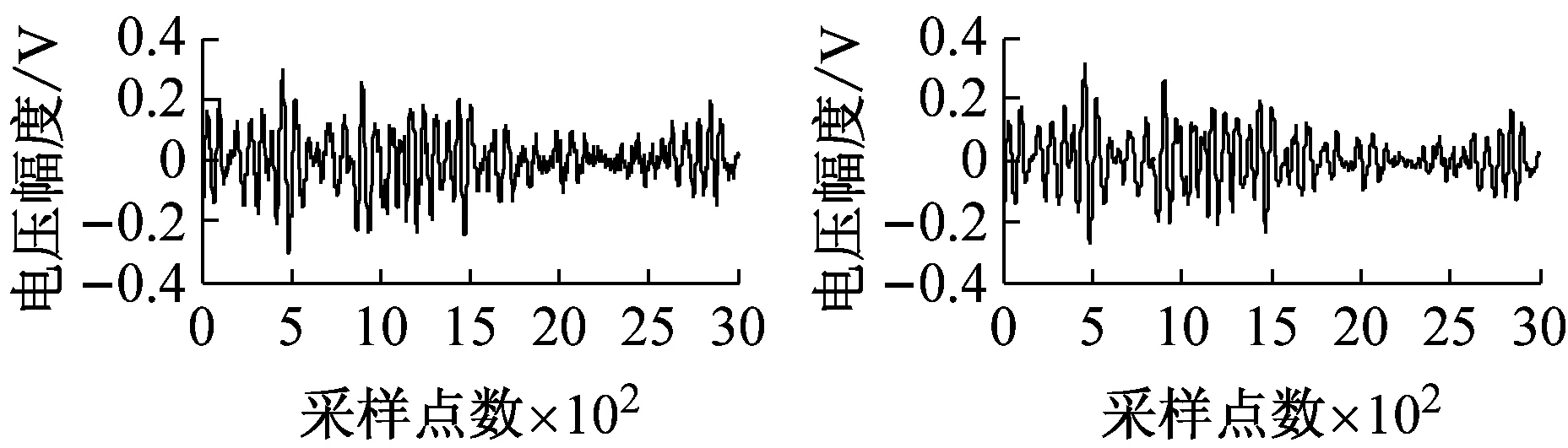
由图5可知,虽然与去白噪声相比,去噪效果不很显著,但该方法对粉红噪声也可以起到降噪作用。
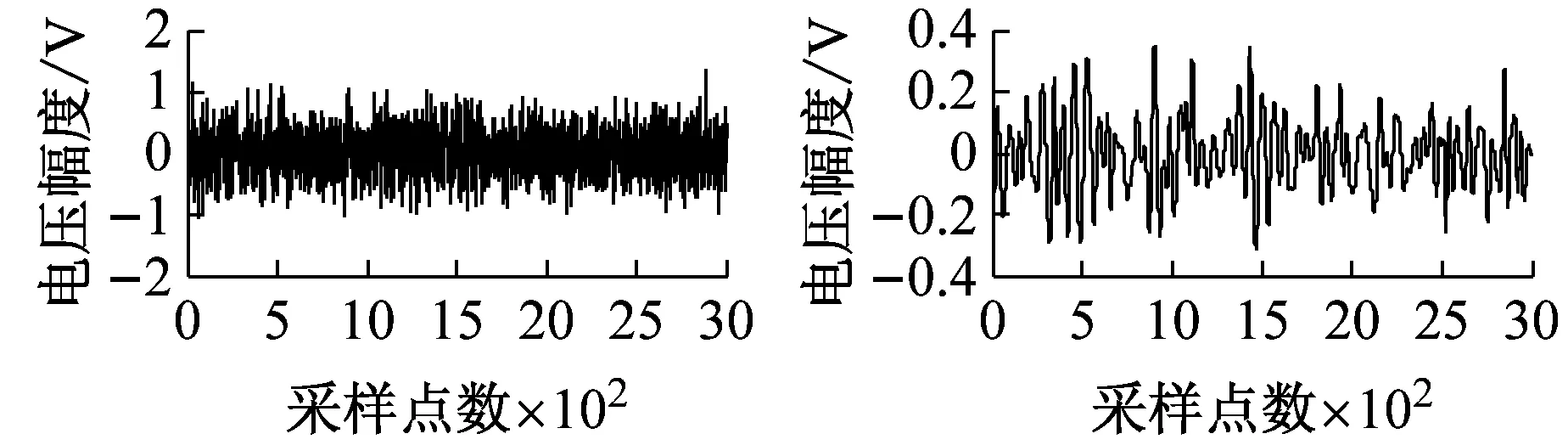
(a) SNRin=-12 dB
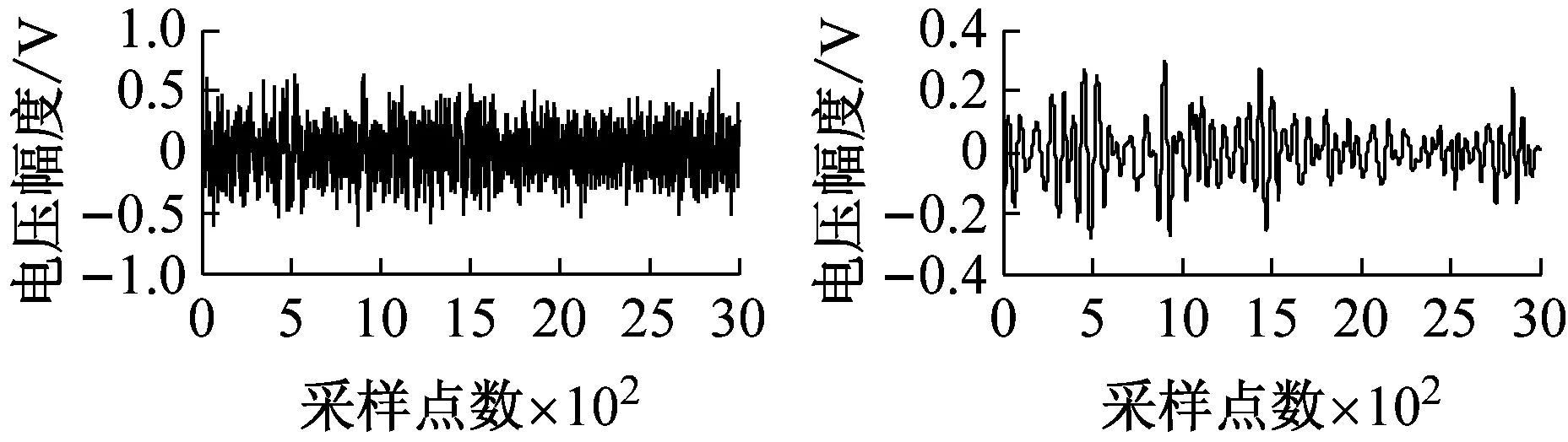
(b) SNRin=-6 dB
(c) SNRin=0 dB
(d) SNRin=6 dB
(e) SNRin=12 dB
(f) SNRin=18 dB
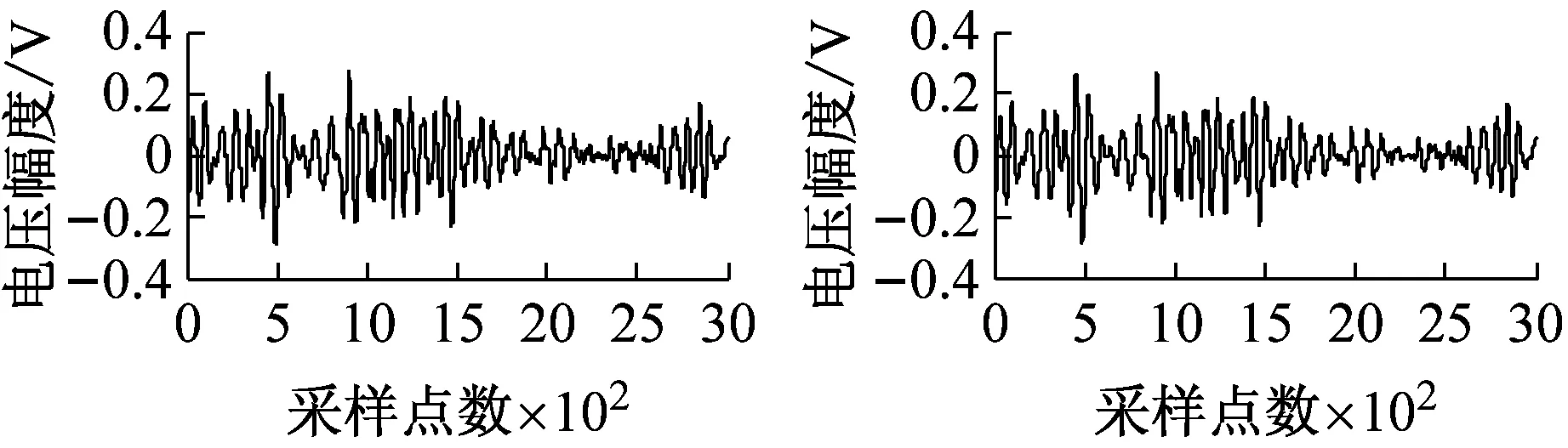
(g) SNRin=24 dB
图4 加入不同信噪比白噪声的碰摩AE信号及降噪后的波形
Fig.4 The rub-impact AE signal before and after white noise reduction waveform at different SNRin
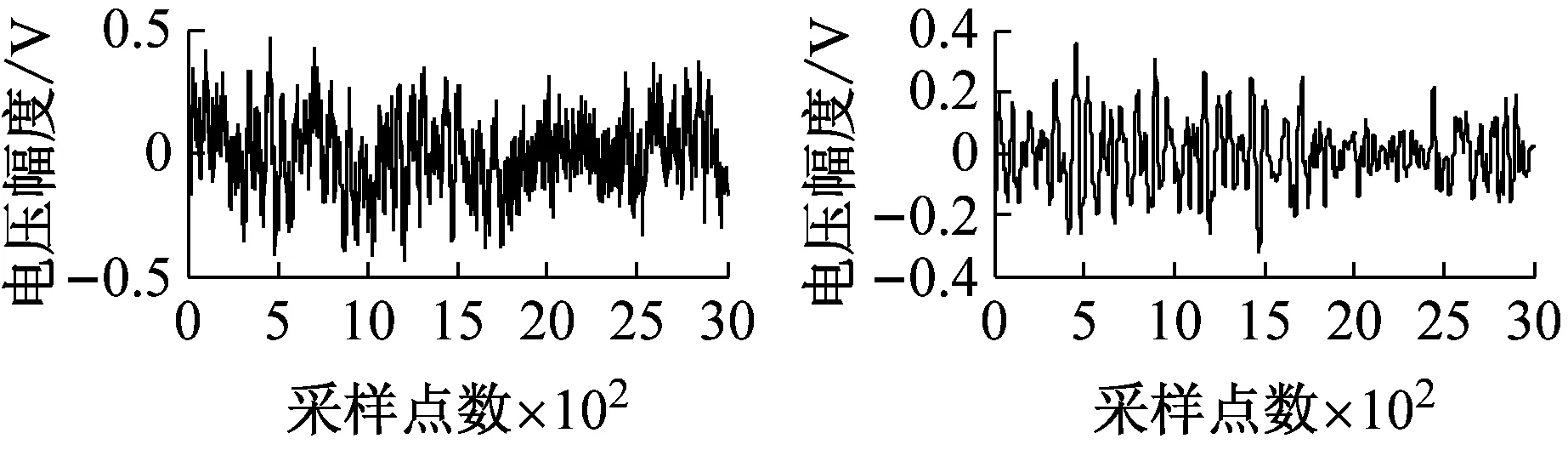
(a) SNRin=-3 dB
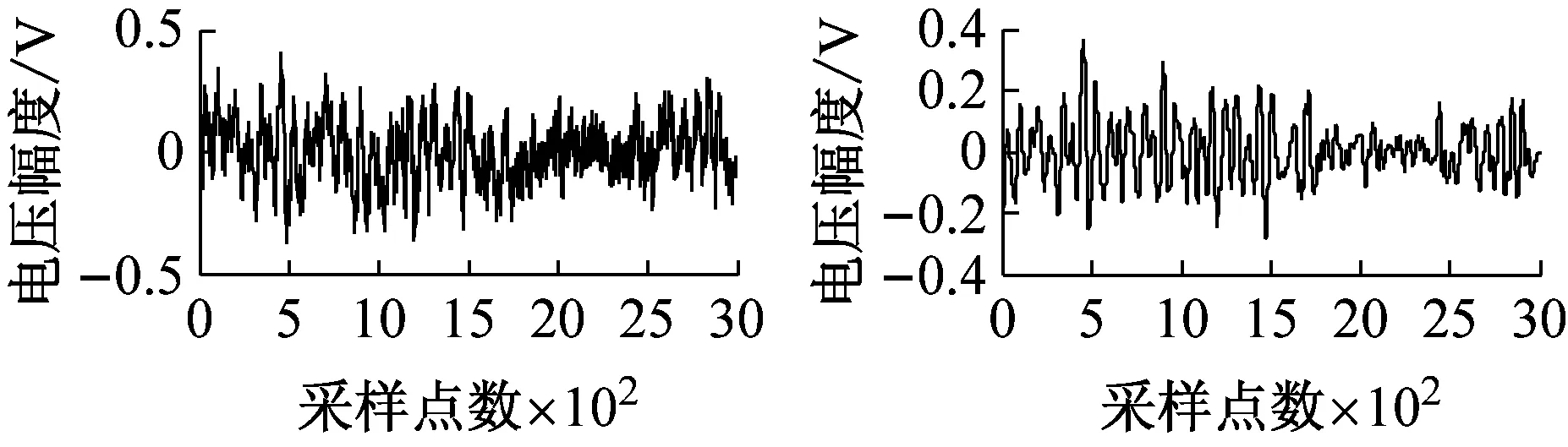
(b) SNRin=0 dB
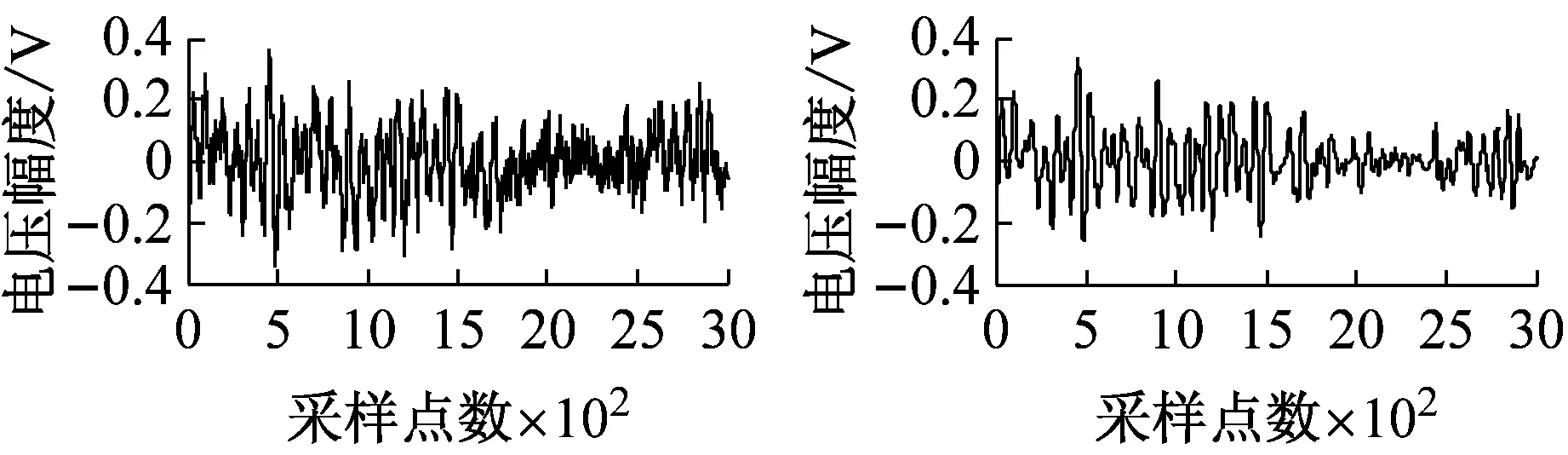
(c) SNRin=3 dB
(d) SNRin=6 dB
(e) SNRin=9 dB
(f) SNRin=12 dB

(g) SNRin=15 dB图5 加入不同信噪比粉红噪声的碰摩AE信号及降噪后的波形Fig.5 The rub-impact AE signal before and after pink noise reduction waveform at different SNRin
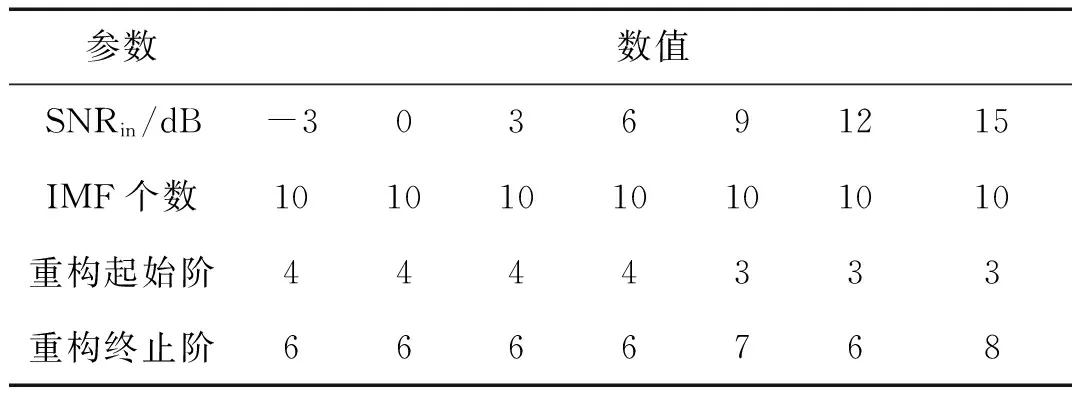
表2 含粉红噪声信号经EMD后情况Tab.2 The signal condition with pink noise after EMD
本文同时采用了小波阈值方法对含噪信号进行了降噪,并与EMD方法作了对比。其中,选择的阈值函数为软阈值函数[14]
(13)
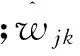
同时选用“sym12”小波基,4层小波分解,启发式阈值(Heursure)和在渐近意义下最优的通用阈值[15]
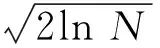
(14)
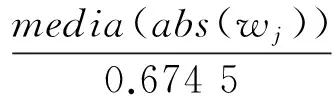
表3为加入不同SNRin的白噪声时,EMD方法和两种小波方法的去噪效果比较。
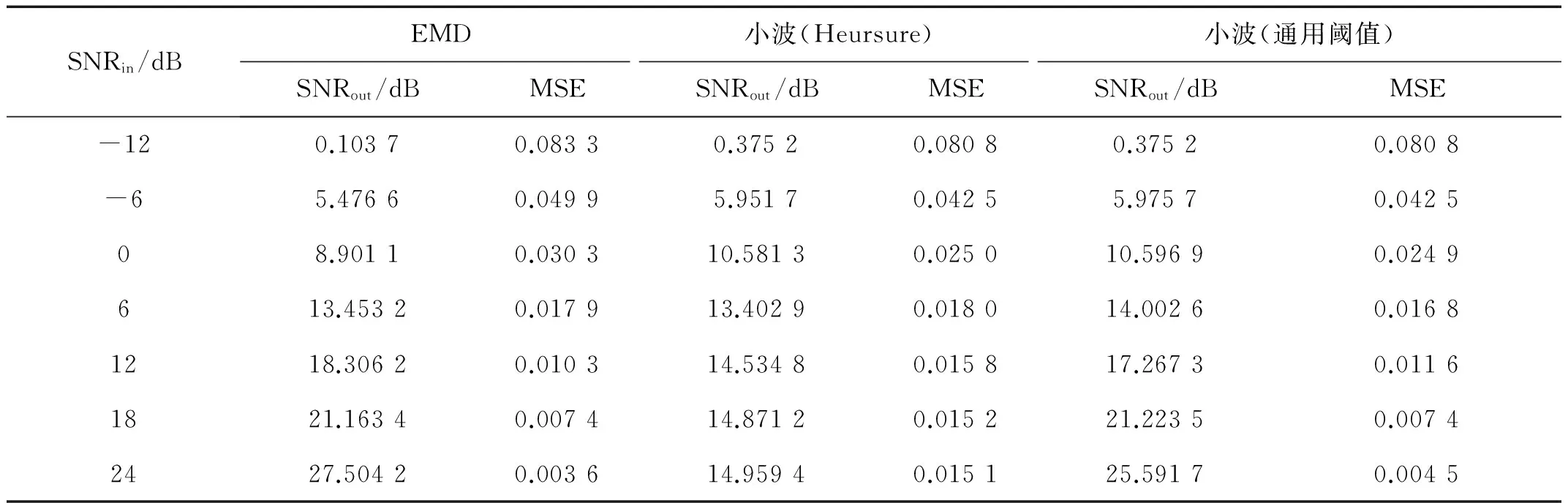
表3 不同去白噪声方法效果比较Tab.3 Comparisions between different kinds of white noise reduction method effect
由表3知,当SNRin=-12 dB时,由于信号过于微弱,三种降噪方式效果都很差。当SNRin>-6 dB时,三种方法都表现出了良好的降噪效果。虽然EMD方法在SNRin=0 dB时SNRout略小于小波方法,但由于此时SNRout与SNRin的比值较大,其降噪效果也是满意的。当SNRin=12 dB时,小波(Heursure)方法效果差于另两种方法,且随着SNRin增大,其SNRout几乎没有改善,不但不能降噪,反而会弱化信号特征,造成信号失真的情况,而EMD和小波(通用阈值)法都表现出较好的降噪能力,且EMD法略优于小波(通用阈值)法。
表4为加入不同SNRin的粉红噪声时,EMD方法和两种小波方法的去噪效果比较。
由表4可知,无论从降噪范围还是降噪效果,EMD方法都是最优的。但与对白噪声去噪相比,EMD方法的效果有所降低,这是由于粉红噪声的频率分量功率主要分布在中低频段,与碰摩AE信号的功率分布接近,使得在重构IMF中存在着相对于白噪声能量更大的粉红噪声的缘故。
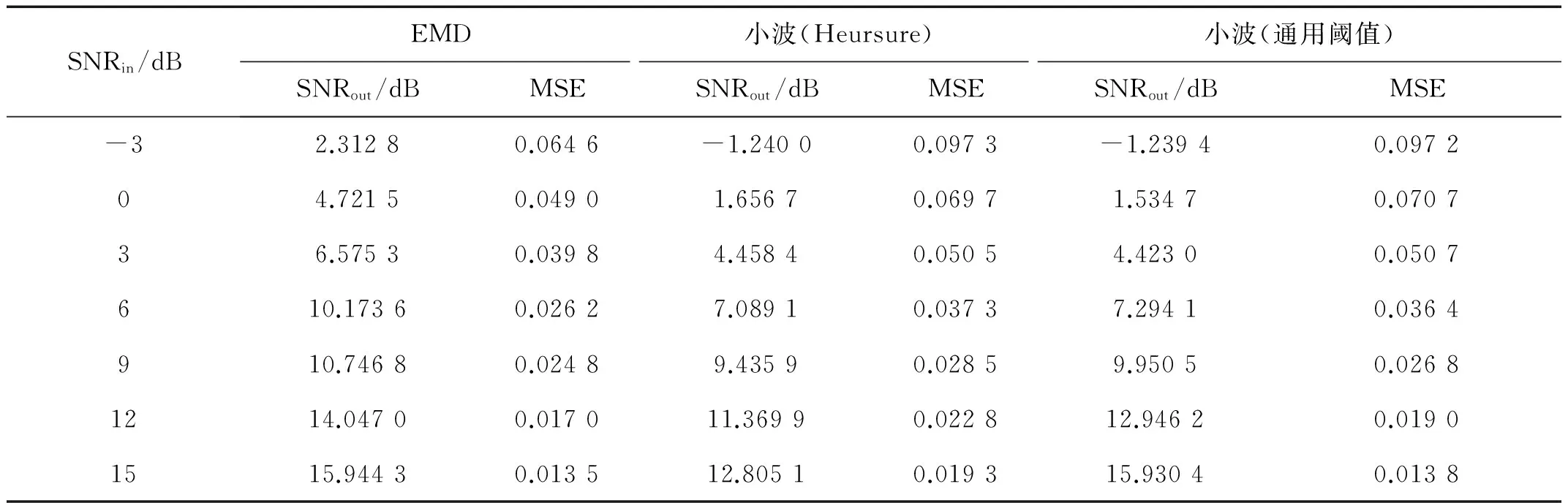
表4 不同去粉红噪声方法结果比较Tab.4 Comparisions between different kinds of pink noise reduction method effect
4 结 论
本文提出了一种基于相关系数法的EMD去除白噪声和粉红噪声的方法,并将其应用在旋转机械碰摩AE信号的降噪处理中。实验结果表明,在去除白噪声时,该方法可以取得与小波阈值法相近的效果;在去除粉红噪声时,该方法的性能优于小波阈值法。该方法充分利用了EMD的滤波特性,是一种信号自适应方法,理论简洁,实现方便,避免了小波阈值法去噪时小波基函数、分解层数、阈值选取及结果不稳定等问题,在处理非线性非平稳信号时具有很大的优势,为旋转机械碰摩AE信号的去噪方式提供了新的思路,对于强噪声环境下的故障信号处理具有实际应用价值。
[1] 孟传民,邓艾东,蒋章,等.转子碰摩故障的声发射与振动特征分析[J].汽轮机技术,2010,52(6):443-446.
MENG Chuanmin,DENG Aidong,JIANG Zhang,et al.Experimental analysis of characteristic of AE and vibration in rotor rub-impact fault[J].Turbine Technology,2010,52(6):443-446.
[2] MBA D.Applicability of acoustic emissions to monitoring the mechanical integrity of bolted structures in low speed rotating machinery:case study[J].NDT&E International,2002,35(5):293-300.
[3] DONOHO D L.De-noising by soft-thresholding [J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[4] 陈果.基于小波分析的转子故障信号自适应降噪技术研究[J].航空动力学报,2008,23(1): 9-16.
CHEN Guo. Research on self-adaptive de-noising technique for rotor faults signal based on wavelet analysis[J].Journal of Aerospace Power, 2008,23(1): 9-16.
[5] HUANG N E, SHIN Z, LONG S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A,1998,454 (1971):903-995.
[6] HUANG B, KUNOTH A. An optimization based empirical mode decomposition scheme[J]. Journal of Computational and Applied Mathematics,2013,240(1):174-183.
[7] 谭善文,秦树人,汤宝平.Hilbert-Huang变换的滤波特性及其应用[J].重庆大学学报,2004, 27 (2): 9-12.
TAN Shanwen,QIN Shuren,TANG Baoping.The filtering character of Hilbert-Huang transform and its application[J].Journal of Chongqing University,2004, 27 (2): 9-12.
[8] 陈隽,李想.运用总体经验模式分解的疲劳信号降噪方法[J].振动、测试与诊断,2011, 31(1): 15-19.
CHEN Jun,LI Xiang.Application of ensemble empirical mode decomposition to noise reduction of fatigue signal[J].Journal of Vibration,Mearsurement&Diagnosis, 2011, 31(1): 15-19.
[9] BOUDRAA A O, CEXUS J C.EMD-based signal filtering[J]. IEEE Transactions on Instrumentation and Measurement,2007,56(6):2196-2202.
[10] 孙伟峰,彭玉华,许建华.基于EMD的激光超声信号去噪方法[J].山东大学学报(工学版),2008, 38(5):1-6.
SUN Weifeng,PENG Yuhua,XU Jianhua.A de-noising method for laser ultrasonic signal based on EMD[J].Journal of Shandong University(Engineering Science), 2008, 38(5):1-6.
[11] 王婷.EMD算法及其在信号去噪中的应用[D]. 哈尔滨:哈尔滨工程大学, 2010.
[12] 程军圣,于德介,杨宇.EMD方法在转子局部碰摩故障诊断中的应用[J].振动、测试与诊断,2006,26(1):24-27.
CHENG Junsheng,YU Dejie,YANG Yu.Application of EMD to local rub-impact fault diagnosis in rotor systems[J]. Journal of Vibration,Mearsurement&Diagnosis,2006,26(1):24-27.
[13] 邓艾东. 基于声发射的旋转机械碰摩故障诊断基础问题研究[D]. 南京:东南大学, 2008.
[14] ZHENG G T,MCFADDEN P D. A time-frequency distribution for analysis of signals with transient components and its application to vibration analysis [J].Journal of Vibration and Acoustics-Transactions of the ASME, 1999,121(3):328-333.
[15] DONOHO D L. Ideal spatial adaptation via wavelet shrinkage[J].Biometrika, 1994,81(3): 425-455.
De-noisingmethodforfaultacousticemissionsignalsbasedontheEMDandcorrelationcoefficient
LIU Dongying1, DENG Aidong1, LIU Zhenyuan2, LI Jing3, ZHANG Rui1, HUANG Hongwei4
(1. National Engineering Research Center of Turbo-generator Vibration, Southeast University, Nanjing 210096, China;2. Ningbo Water Supply Co., Ltd.,Ningbo 315041, China; 3. School of Information Science and Engineering, Southeast University, Nanjing 210096, China; 4. SPIC Henan Power Limited Company Technology & Information Center, Zhengzhou 450001, China)
A number of non-stationary and non-linear noises often interfere with the useful acoustic emission(AE)signals which induces the difficulty in AE recognition.Based on the principle of correlation coefficient,a de-noising method for rubbing AE signals of rotating machines based on the empirical mode decomposition(EMD) was proposed.The original noise polluted AE signal was divided into several intrinsic mode functions(IMFs) derived from the EMD.Through calculating each correlation coefficient between IMFs and AE siginal, finding out their changing regularities and considering the EMD’s filtering characteristic, the modes reflecting the important structures of the signal were chosen and combined to reconstruct a de-noised signal.Simulations were conducted for rub-impact AE signals polluted by different kinds of noises using this method. The experimental results indicate that the method can not only effectively and adaptively remove noises,but also get the stable results which are not affected by subjective parameters.
rub-impact; acoustic emission; signal de-noising; empirical mode decompositon (EMD); correlation coefficient
TH165
A
10.13465/j.cnki.jvs.2017.19.011
国家工程中心创新能力建设项目(6750100000)
2016-05-10 修改稿收到日期:2016-07-18
刘东瀛 男,硕士,1992年5月生
邓艾东 男,博士,教授,博士生导师,1968年8月生
