分层排序集抽样下的比率估计问题探讨

陈晓旭，朱永忠

（河海大学 理学院，南京211100）

分层排序集抽样下的比率估计问题探讨

陈晓旭，朱永忠

（河海大学 理学院，南京211100）

分层排序集抽样是指将分层抽样与排序集抽样结合起来，运用分层技术将总体分为多层，再在每层中用排序集抽样获取样本。分层比率估计是利用辅助信息，构造总体均值或总值的估计量，分为联合比率估计和分别比率估计。文章利用此思路得到下分层排序集抽样下总体均值的分别比率估计，并和分层排序集抽样下的联合比率估计、分层随机抽样下的分别比率估计进行比较。结果表明，分层排序集抽样下总体均值的分别比率估计比分层随机抽样下总体均值的分别比率估计效果好，分层排序集抽样下总体均值的联合比率估计比分层排序集抽样下总体均值的分别比率估计效果好。

分层随机抽样；分层排序集抽样；分别比率估计；联合比率估计

0 引言

众所周知，统计认识活动的一个重要环节是通过统计调查获取统计数据，然后再据以进行科学的统计分析，而在实际问题中，我们所要研究的事物的数量总是很庞大，获得全部需要的数据是不易的，或者是不可能实现的，这就给我们研究事物的总体特征带来了不便，抽样技术的应用就很好地解决了这个问题，不必获取全部个体信息，而是利用样本代表总体。好的抽样方法能节省调查费用，增强调查的时效性，有助于提高数据的质量，承担全面调查难以胜任的调查任务，所得的样本能很好地描述总体的特征。排序集抽样就是一种有效的抽样方法。

排序集抽样（RSS）最初由McIntyre[1]于1952提出，Takahasi和Wakimato[2]证明了排序集抽样在估计总体均值方面比简单随机抽样具有更小的方差。由于排序集抽样的优良性，因此排序集抽样受到了很多国外专家的关注。Samawi H M[3]讨论了排序集抽样下总体均值的比率估计问题。Kadilar C和Unyazici Y[4]对排序集抽样下总体均值的比率估计问题进行了改进，提出了新的估计量。Jozani M J等[5]用比率估计的改进形式解决了比率估计的无偏性问题。乔松珊等[6]基于排序集样本建立了总体均值的估计量，并证明在给定估计精度下，分层排序集抽样方法可以有效降低抽样调查费用。

由于分层随机抽样下的比率估计有两种情形，一种是分别比率估计，另一种是联合比率估计。在大样本情况下，分别比率估计比联合比率估计效果要好。因此分层排序集抽样下的比率估计也应该有两种形式。已有文献中研究的是分层排序集抽样下运用联合比率估计求指标的总数或均值，且证明了分层排序集抽样下联合比率估计比分层简单随机抽样的效果好。因此本文考虑在分层排序集抽样下用分别比率估计来求指标的均值，并和分层排序集抽样下的联合比率估计量、分层随机抽样下的分别比率估计量进行比较。

1 排序集抽样方法和分别比率估计

排序集抽样方法是一种抽样设计方法。分层排序集抽样是指先将总体分层，再将排序集抽样应用到总体的每一层中。具体抽样过程如下：

设(X,Y)构成二维总体，利用辅助信息X将总体分成L层。在每一层中进行排序集抽样。在第h层的具体抽样过程是：mh表示第h层所要抽取的样本容量，先从第h层抽取mh2个简单随机样本，然后将这mh2个样本随机划分成mh组，每组mh个个体，依据辅助变量X的信息，对每组个体进行由小到大排序，从第一组中抽取次序最小的个体进行测量，记为(Xh(1),Yh(1))，从第二组样本中抽取次序第二小的样本个体进行测量，记为(Xh(2),Yh(2))，以此类推，直到从第mh组中抽取次序最大的样本(Xh(mh),Yh(mh))。将上述过程重复r次，得到到样本量为mr的分层排序集样本，其中m=m1+m2+…+mh，各层样本量nh=mh×r。最终得到的样本为{(Xh(1)k,Yh(1)k),(Xh(2)k,Yh(2)k),…,(Xh(mh)k,Yh(mh)k)}，k=1,…,r；h=1,…,L。其中Xh(i)k是第k次在第h层抽取排在第i的样本，Yh(i)k为伴随变量，i=1,…,mh。则变量X,Y在第h层的样本均值分别为从第h层总体中抽取了r×mh2个样本，但实际测量的个体只有r×mh个，而这r×mh个样本却代表了r×mh2个样本的信息量，因此排序集抽样于简单随机抽样（SRS）相比，前者对总体均值的估计更为精确。

比率估计是利用辅助变量的信息改进估计的方法，是利用目标变量和辅助变量的比例关系来提高估计的精度。比率估计涉及的是两个指标，且两个指标都要通过样本进行估计。分层抽样中的比率估计有两种情形：一是分层之后，先在各层获取比率估计，然后按照层权加权平均得到总体参数估计；二是先分别对目标变量、辅助变量作分层估计，然后再采用比率估计方法。前者称为分别比率估计，后者称为联合比率估计。因为比率估计是有偏的，只有在大样本下偏倚才近似为零，所以具体采用分别比率估计还是联合比率估计还要结合具体情况讨论。如果各层的样本量都较大，则可以采用分别比率估计；如果各层只是小样本，则最好采用联合比率估计。

2 分层排序集抽样（RSS）和分层随机抽样（SRS）下的比率估计

2．1 分层随机抽样下分别比率估计

分层随机抽样下，用每层估计在总体权重的加权平均去估计总体均值。由文献[7]知，总体均值μY的分别比率估计量为：

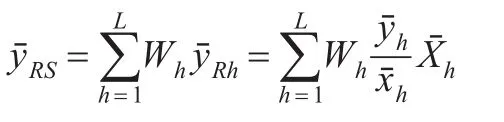
其中X为已知辅助变量，表示第h层的层权，,分别为变量X,Y在第h层的样本均值，为变量X在第h层的总体均值，为第h层总体比率的估计Rh。

当样本量足够大时，有：

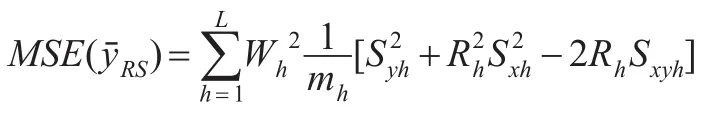
2．2 分层排序集抽样下联合比率估计

由文献[6]知，在RSS抽样下得到总体均值的联合比率估计为：

2．3 分层排序集抽样下分别比率估计

在RSS抽样下得到总体均值μY的分别比率估计为：

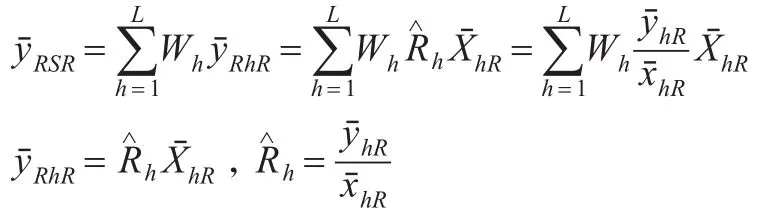
其中表示第h层的总体均值，表示第h层总体比率Rh的估计，，表示变量X,Y在第h层的样本均值。

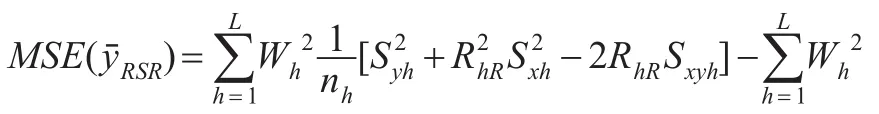
证明：

由文献[3]可知：

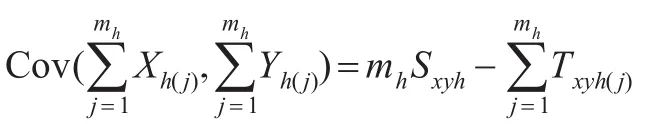
故：

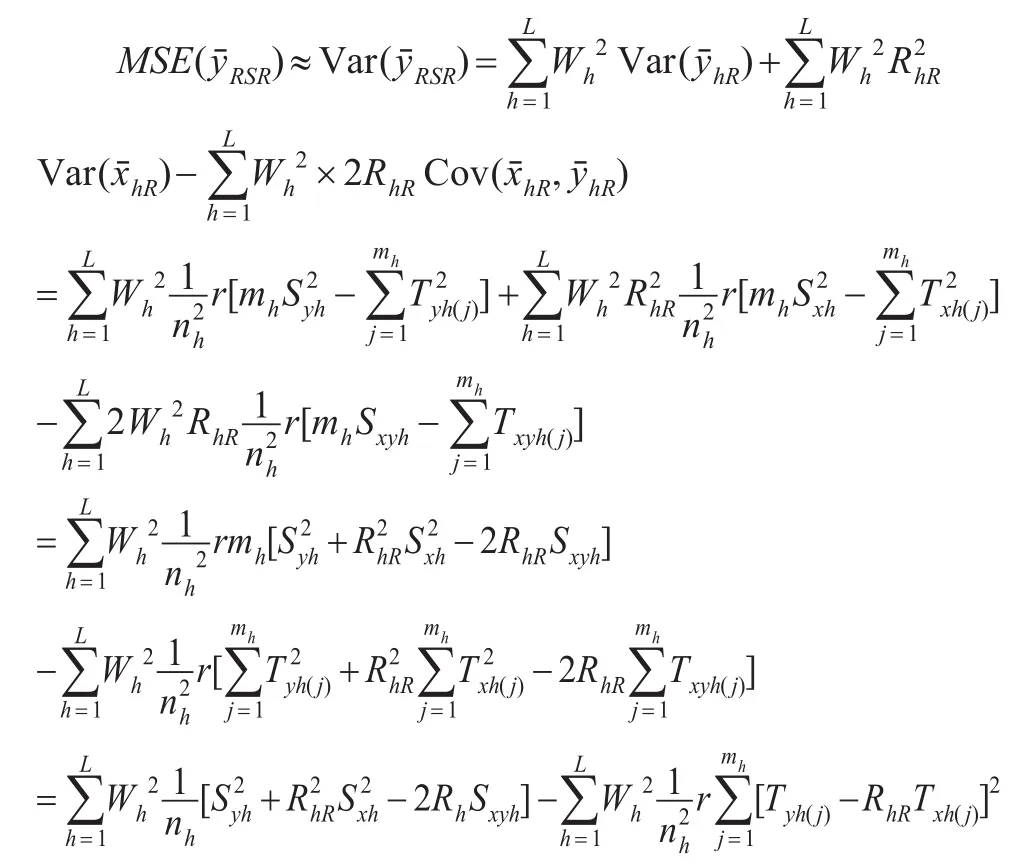
因此：

RSS抽样比SRS抽样获得的样本信息量更大，且由以上 证 明 可 知，因此分层排序集抽样对总体均值估计量的均方误差更小，使得估计更加精确。

3 数据模拟

上文已经证明了基于分层排序集抽样得到的总体均值的分别比率估计量比基于分层随机抽样得到的总体均值的分别比率估计量要好。现在进行数据模拟，二维随机观测值产生于一个总体为二维的正态分布，这里模拟的正态分布为N(2,4,1,1,ρ)，ρ为随机变量的相关系数，分层的层数L=5。mi表示第i层样本数，m=(m1,m2,m3,m4,m5)′表示不同层的样本数取值向量，给出不同的层样本数，研究其变化规律。ρ也是影响总体均值比率估计量的一个变量。用R语言编程模拟，程序循环1000次，可以输出分层排序集抽样和分层随机抽样下总体均值估计量的均方误差。数据模拟结果如表1所示。

从表1中的数据可以看出，给定m时，相关系数ρ越大，MSE()、MSE() 、MSE()均越小，但不论X,Y的相关系数如何，MSE() 总比MSE()小，MSE() 总比MSE()小；ρ相同时，随着m的增大，MSE()、MSE()、MSE()均越来越小，但不论m为多少，MSE() 总比MSE()小，MSE() 总比MSE()小。因此，可得出结论：分层排序集抽样下总体均值的分别比率估计比分层随机抽样下总体均值的分别比率估计的均方误差更小；分层排序集抽样下总体均值的联合比率估计比分层排序集抽样下总体均值的分别比率估计的均方误差更小。

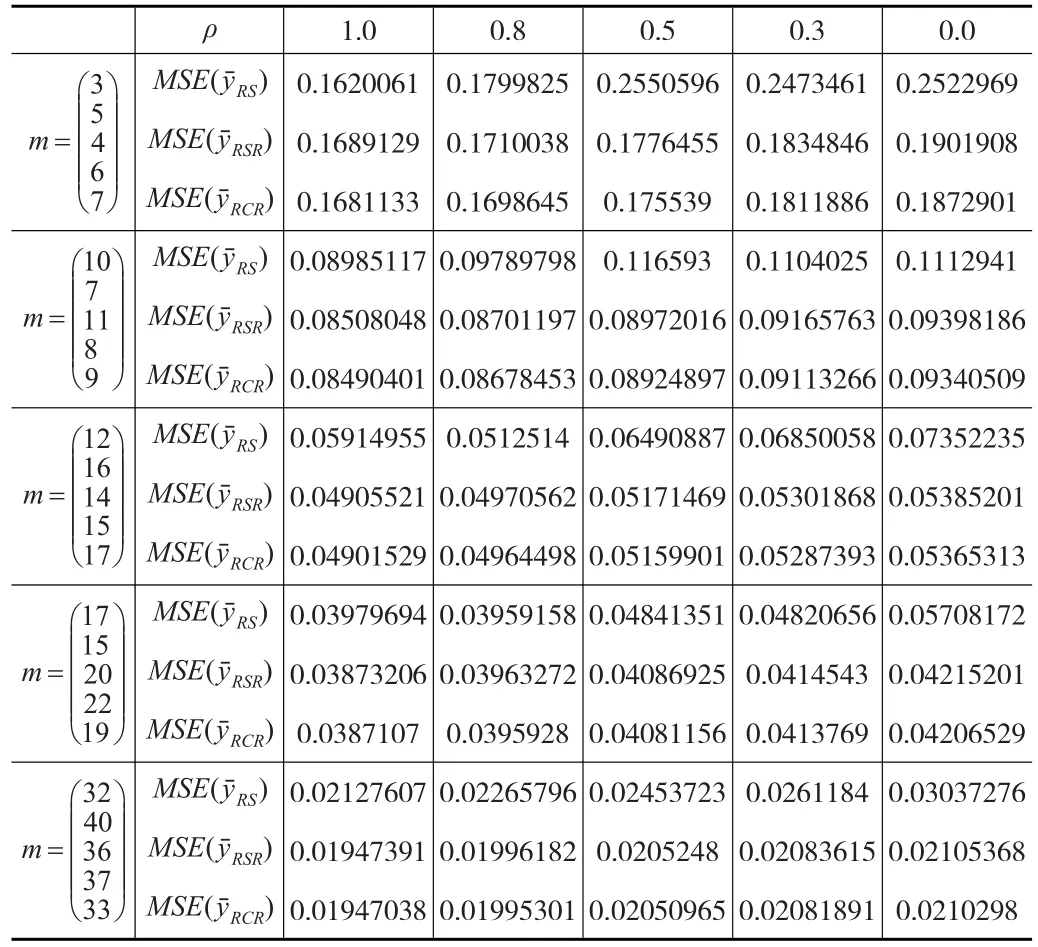
表1 数据模拟结果

4 结论

排序集抽样是一种新的获取样本的抽样方法。当我们面对的总体规模较大时，要想得到总体特征，需要考虑缩小总体规模，同时尽量使得总体中个体之间差异减小，因此采用分层抽样比较合适。当总体的指标调查困难，而又有其他辅助指标可供利用，因此可采用比率估计。

本文把排序集抽样对总体均值的比率估计以及分层随机抽样对总体均值的比率估计结合起来，将排序集抽样设计运用到分层抽样的每一层，以用于对总体均值的比率估计。本文比较了三种估计量的均方误差，从理论上证明了分层排序集抽样总体均值的分别比率估计量比分层随机抽样下总体均值的分别比率估计量更有效。通过数据模拟，表明分层排序集抽样总体均值联合比率估计量比分别比率估计量具有更小误差，分层排序集抽样总体均值分别比率估计量比分层随机抽样下总体均值分别比率估计量具有更小误差。

[1]McIntyre G A.A Method for Unbiased Selective Sampling,Using Ranked Sets[J].Australian Journal of Agriculture Research,1952,(3).

[2]Takahasi K,Wakimoto K.On Unbiased Estimates of the Population Mean Based on the Sample Stratified by Means of Ordering[J].Annals of the Institute of Statistical Mathematics,1968,(21).

[3]Samawi H M.Estimation of Ratio Using Rank Set Sampling[J].Biom J,1996,38(5).

[4]Kadilar C,Unyazici Y.Ratio Estimation for the Population Mean Using Ranked Set Sampling[J].Stat Papers,2009,50(2).

[5]Jozani M J,Majidi S.Unbiased and Almost Unbiased Ratio Estimators of the Population Mean in Ranked Set Sampling[J].Stat Papers,2012,53(2).

[6]乔松珊,张建军.基于辅助信息额分层排序集抽样及调查费用分析[J].数学的实践与认识,2015,45(13).

[7]金进勇.抽样:理论与应用[M].北京:高等教育出版社,2010.

Discussion on Ratio Estimation of Hierarchical Ranked Set Sampling

Chen Xiaoxu，Zhu Yongzhong

(School of Science,Hohai University，Nanjing 211100，China)

Hierarchical ranked set sampling refers to the combination of ranked set sampling with hierarchical sampling,and dividing the population into multi layers through layering technology,and then using ranked set to acquire samples from each layer.Hierarchical ratio estimation means using auxiliary information to construct the estimator of population mean or the total value,and it includes combined ratio estimation and respective ratio estimation.This paper utilizes this idea to get the respective ratio estimation of the population mean under the hierarchical ranked set sampling,and compare it with the combined ratio estimator under the hierarchical ranked set sampling and respective ratio estimation under the hierarchical random sampling.The study results show that the respective ratio estimation of the population mean under the hierarchical ranked set sampling is more efficient than respective ratio estimation under the hierarchical random sampling,and that the combined ratio estimation under the hierarchical ranked set sampling is more efficient than respective ratio estimation of the population mean under the hierarchical ranked set sampling.

hierarchical random sampling;hierarchical ranked set sampling;respective ratio estimation;combined ratio estimation

O212.2

A

1002-6487（2017）20-0015-04

国家自然科学基金资助项目（50979029）

陈晓旭（1991—），女，湖北钟祥人，硕士研究生，研究方向：统计分析方法。

朱永忠（1968—），男，江西瑞昌人，博士，教授，研究方向：统计与随机过程。

(责任编辑/亦 民)