基于MCKD和VMD的滚动轴承微弱故障特征提取

夏均忠， 赵 磊， 白云川， 于明奇， 汪治安

(军事交通学院 军用车辆工程技术研究中心，天津 300161)

基于MCKD和VMD的滚动轴承微弱故障特征提取

夏均忠， 赵 磊， 白云川， 于明奇， 汪治安

(军事交通学院 军用车辆工程技术研究中心，天津 300161)

针对滚动轴承早期故障特征非常微弱，易受随机噪声和其他信号干扰而难以提取等现象，提出了用最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution，MCKD)和变分模态分解(Variational Mode Decomposition，VMD)相结合的方法提取滚动轴承故障特征。首先用MCKD进行信号增强，然后利用VMD得到一系列模态，应用互相关系数和峭度准则筛选包含故障信息较为丰富的模态进行重构降噪，最后对重构信号进行包络解调提取故障特征。通过仿真分析和轴承故障模拟实验验证了该方法的有效性，可以精确地分离轴承故障振动信号的不同频率成分。

滚动轴承；最大相关峭度解卷积；变分模态分解；互相关系数；峭度准则

滚动轴承频发的各种故障大部分以局部缺陷的形式发生在轴承工作周期的早期，而且多数是潜在故障，具有特征信息微弱、易被噪声淹没及信噪比低等特点，使得产生的周期性脉冲往往淹没在背景噪声当中不易识别和提取。为了准确提取轴承早期微弱故障特征，排除噪声对信号的干扰，需要增强周期冲击信号、降低噪声来提高信噪比。

最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution，MCKD)是McDonald等[1]在最小熵解卷积的基础上提出的一种新的增强信号周期性冲击成分的解卷积技术，并应用于齿轮的故障诊断。该方法以相关峭度为评价指标，通过迭代过程实现解卷积，进而突出信号中被噪声淹没的连续脉冲序列。文献[2]应用MCKD预处理信号，再使用1.5维谱分析判断轴承故障特征频率成分，有效地提取了早期故障特征信息。文献[3]针对机械信号中存在的噪声会降低重分配小波尺度谱的时频分布可读性，提出基于MCKD和重分配小波尺度谱的方法对旋转机械复合故障进行诊断。

经验模态分解(Empirical Mode Decomposition，EMD)是Huang在上个世纪末期提出的一种分析非线性、非平稳信号的递归式模态分解方法[4]。由于缺乏良好的数学理论以及在分解时容易受到噪声和采样率的限制，EMD存在一些问题，如模态混叠、端点效应以及过包络、欠包络等。鉴于此，Dragomiretskiy K和Zosso D于2014年提出了一种新的非递归式自适应模态分解算法——变分模态分解(Variational Mode Decomposition，VMD)[5]。文献[6]应用VMD和消除趋势波动分析对信号进行降噪处理。

为了增强轴承故障振动信号中的周期性冲击成分，降低噪声的干扰，更加精确地提取轴承故障特征，提出了基于MCKD和VMD的滚动轴承微弱故障特征提取方法。首先用MCKD对轴承振动信号进行增强，然后利用VMD得到一系列模态，并结合互相关系数和峭度准则筛选包含故障信息较为丰富的模态进行重构降噪，最后对重构信号进行包络解调，精确有效地提取出滚动轴承故障特征频率。

1 最大相关峭度解卷积(MCKD)

MCKD的本质就是寻找一个FIR滤波器f(l)(l为滤波器的长度)，使原始冲击序列的相关峭度最大，以此恢复其所具有的特性，达到增强信号的目的。

相关峭度的定义为

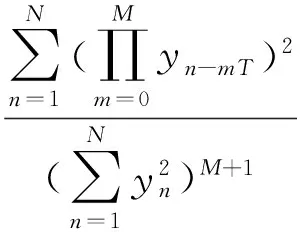
(1)

为选取一个最优滤波器f(l)，使CKM(T)最大，令

(2)

式中：T为冲击信号的周期；M为位移数；f为滤波器向量，f=[f1,f2,…,fL]T；L为FIR滤波器的长度。

上述优化求解问题等价于求解方程

(3)

用矩阵的形式来表示最终的滤波器系数

(4)

其中：

r=[0T2T…mT]

通过迭代方式求滤波器f参数的过程如下：

(1) 确定周期T、移位数M和滤波器的长度L。

(3) 计算滤波后的输出信号y。

(4) 根据y计算αm和β。

(5) 计算新滤波器的系数f。

(6) 如果滤波前后信号的ΔCKM(T)>ε时，跳转到步骤(3)继续循环，否则停止递归。ε是用来控制迭代终止的较小正数。

2 变分模态分解(VMD)

2.1 基本原理

VMD是一种完全非递归的信号分解方法。它可以将任意信号f(t)分解成许多围绕在中心频率ωk周围的模态分量信号。具体步骤如下：

(1) 首先用Hilbert变换计算每个模态uk的相关解析信号以获得一个单边频谱，然后通过加入一个指数项来调整各自估计的中心频率，把每个模态的频谱转移到基带上，最后通过解调信号的高斯平滑来估计带宽，即梯度的二范数平方。由此产生了一个由变分问题组成的目标函数

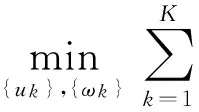
(5)

(2) 通过引入拉格朗日乘子λ和二次惩罚项将上述约束性变分问题转化为非约束性变分问题。增广拉格朗日表达式如下

(6)

式中：α为惩罚因子；λ(t)是加强约束。二次惩罚项的作用是提高收敛性。

(3) 通过寻找迭代子优化序列中增广拉格朗日的鞍点，即应用交替方向乘子法(优化算法)求解式(5)的最小化问题。求解式(6)的迭代方法为

(7)

(8)

(9)

(10)

式(10)为收敛条件，ε为精度(ε>0)，n为迭代次数。

利用L2范数下Parseval/Plancherel傅里叶等距变换在频域对式(7)～式(9)进行求解

(11)

(12)

(13)

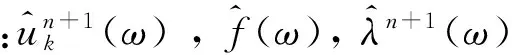
因此，完整的VMD算法实现过程如下：

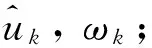
一团玫瑰的甜香随即旋转到夏天的身边，他知道是叶晓晓刚刚洗完澡，稍稍定了定神，说：“晓晓，我渴了，能给我倒杯水吗？”

(3) 对于所有的ω≥0：

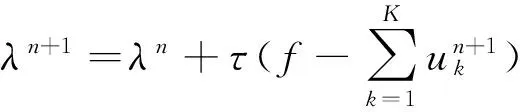
(4) 判断是否满足式(10)的收敛条件，若满足则停止迭代，否则返回到步骤(2)。

2.2VMD和EMD的对比分析

设包含噪声的仿真信号为

(14)

式中：f1=2，f2=24，f3=288，n(t)为随机噪声,采样频率为1 000 Hz，采样点数为1 000个。仿真信号的波形如图1所示。分别对其进行EMD和VMD分解，得到的分解结果如图2、3所示。EMD分解结果中，IMF1、IMF2包含着高频谐波和噪声，IMF3和IMF4出现了模态混叠现象，IMF4最接近于中频谐波，IMF6包含有低频谐波但出现了严重扭曲。VMD分解结果中，模态U1、U2包含信号的低频、中频成分，模态U3中的高频成分由于噪声的影响较难分辨，但是通过VMD算法可以计算出其中心频率。所以，VMD比EMD分解误差小，而且克服了模态混叠现象，物理意义更明确。

图1 仿真信号的波形图Fig.1 The waveform of simulated signal

图2 EMD分解结果Fig.2 The result of EMD

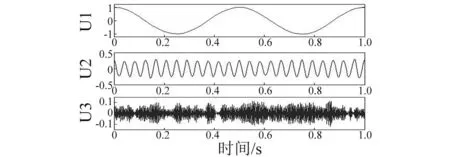
图3 VMD分解结果Fig.3 The result of VMD

3 仿真分析

为验证本文方法的有效性，利用故障模型模拟轴承故障产生的周期性冲击信号，并向其中添加白噪声来模拟轴承早期故障信号[7]。仿真信号如下：

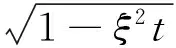
(15)

式中：载波频率fn=3 000 Hz，位移常数x0=5，阻尼系数ξ=0.1，冲击故障的周期T=0.01 s，采样频率fs=20 kHz，采样点数N=4 096，t为采样时刻，n(t)为白噪声。

仿真信号的时域波形和包络谱如图4所示，轴承故障冲击信号已经完全被噪声淹没，无法识别故障信息。对仿真信号进行MCKD信号增强，得到的时域波形和包络谱如图5所示，可以看到时域波形里的冲击信号更加明显，而频谱图中的冲击频率受到噪声影响还不能清晰精确地从中识别出来。

图4 仿真信号的时域波形和包络谱Fig.4 Time-domain and envelope spectrum of the simulated signal

对MCKD处理后的信号进行VMD，根据互相关系数和峭度准则筛选包含故障信息较为丰富的模态分量进行重构降噪，然后对重构信号进行包络解调，得到的包络谱图如图6所示。从图中可以明显看出轴承故障周期冲击频率(100 Hz)及其倍频(200 Hz、300 Hz、400 Hz、500 Hz等)。仿真分析证明了该方法的有效性，适用于强噪声背景下轴承早期故障特征提取。

图5 MCKD处理后的时域波形和包络谱Fig.5 Time-domain and envelope spectrum based on MCKD

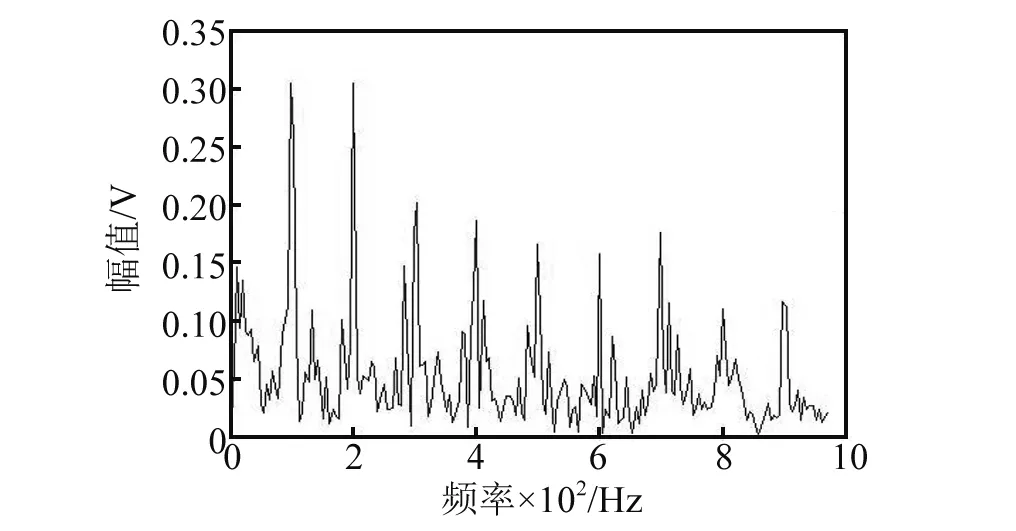
图6 VMD重构后的包络谱Fig.6 Envelope spectrum based on VMD reconstruction

4 滚动轴承故障特征提取

4.1 算法流程

如图7所示为基于MCKD和VMD的滚动轴承故障特征提取流程图，具体步骤如下：

(1) 对采集的振动信号用MCKD增强周期冲击成分；

(2) 对处理后的信号进行VMD分解得到各模态分量；

(3) 取互相关系数和峭度值较大的模态分量进行重构降噪，并求出重构信号的包络谱；

(4) 将滚动轴承故障特征频率与包络谱峰值较大处的频率进行比较，从而精确有效地提取出滚动轴承故障特征。

4.2 应用实例

实验装置由驱动电机、振动加速度传感器、扭矩解码/编码器、联轴器和功率计等组成，如图8所示[8]。试验轴承为SKF 6205-2RS深沟球轴承，其技术参数见表1。使用电火花在轴承内、外圈加工直径均为0.18 mm(深度均为0.28 mm)，模拟内、外圈故障。电机转速为1 750 r/min，采样频率为12 kHz。

图7 滚动轴承故障特征提取流程图Fig.7 Flow chart of rolling element bearing fault feature extraction

图8 实验装置示意图Fig.8 The schematic diagram of experimental device表1 试验轴承技术参数Tab.1 The specification of tested bearing

滚动体直径d/mm节圆直径D/mm内径dm/mm外径Do/mm滚动体数Z接触角α/(°)839255290

如图9所示，为滚动轴承内、外圈故障振动信号的时域波形及频谱。从图中可以发现内、外圈故障信号时域波形由于噪声的影响已无法识别故障特征，且频谱图中出现了一些高频成分。

(a) 内圈故障

(b) 外圈故障图9 轴承振动信号的时域波形及频谱Fig.9 Time-domain waveform and spectrum of bearing vibration signal

对轴承振动信号用MCKD进行增强，信号的时域波形和包络谱如图10所示。内圈故障振动信号的峭度值由5.50增加到10.82，外圈故障振动信号的峭度值由7.84增加到23.05，增加幅度较为明显；时域波形中出现了明显的冲击成分，且频谱中的低频冲击成分较为增强，但是还存在噪声的影响，仍无法清晰识别轴承故障特征频率。

(a) 内圈故障

(b) 外圈故障图10 MCKD处理后的时域波形和包络谱Fig.10 Time-domain and envelope spectrum based on MCKD

再对MCKD增强后的信号进行VMD分解，结果如图11所示。分别计算各模态与原信号的相关系数及其峭度值，见表2。从表中可以看出模态分量U2、U3、U4与原信号的相关系数、峭度值较大，于是选择上述3个模态分量进行信号重构，再对重构后的信号进行包络解调，得到其包络谱如图12所示。

(a) 内圈故障

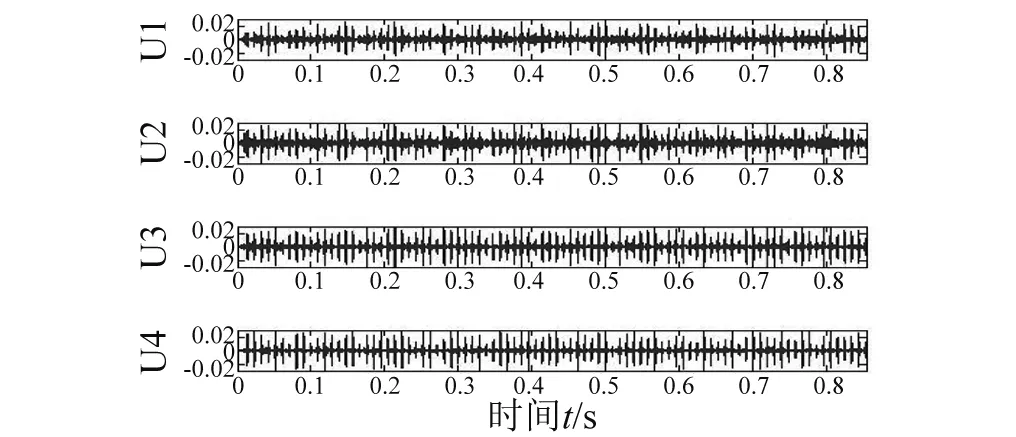
(b) 外圈故障图11 VMD分解结果Fig.11 The result of VMD表2 内、外圈故障的相关系数和峭度值Tab.2 Correlation coefficient and kurtosis of innerand outer race fault

特征参数模态UU1U2U3U4内圈峭度值相关系数3.380.446.490.456.820.534.990.55外圈峭度值相关系数7.850.467.340.558.590.5711.540.53

从图12(a)可以看出，轴承内圈故障时振动信号的包络谱包括回转频率，内圈故障特征频率及其二次谐波(2BPFI=316.26 Hz)、三次谐波(3BPFI=474.39 Hz)，调制边带(BPFI-fr=128.97 Hz、BPFI+fr=187.29 Hz)。从图12(b)可以看出，轴承外圈故障时的振动信号包括回转频率，外圈故障特征频率及其二次谐波(2BPFO=208.60 Hz)、三次谐波(3BPFO=312.90 Hz)、四次谐波(4BPFO=417.20 Hz)、五次谐波(5BPFO=521.50 Hz)。综合分析可以精确判断出滚动轴承内、外圈故障，分析结果与实际相符。因此，基于MCKD和VMD的方法可以精确地提取滚动轴承微弱故障特征频率。

(a) 内圈故障

(b) 外圈故障图12 VMD重构后的包络谱Fig.12 Envelope spectrum based on VMD reconstruction

5 结 论

(1) 滚动轴承故障早期阶段冲击特征非常微弱，而且容易受到其他信号的干扰，MCKD以相关峭度最大化为优化目标，通过迭代过程实现信号的解卷积，增强信号中被强噪声干扰的脉冲冲击，提高了峭度值和信噪比，非常适用于增强轴承早期故障信号的冲击特性。

(2) 故障轴承产生的振动信号中往往含有较多的调幅调频分量，解调后的信号中包含了轴承回转频率及其倍频，故障特征频率及其倍频等调制成分。VMD是一种新的非递归式自适应模态分解方法，它能自适应地确定相关频带，同时估计对应的模态。克服了传统的递归式模态分解(如EMD、LMD)因冲击成分和噪

声引起的模态混叠，可以更加精确地提取不同故障类型的特征信息。

[1] MCDONALD G L，ZHAO Q，ZUO M J．Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]．Mechanical Systems and Signal Processing，2012，33: 237-255.

[2] 唐贵基，王晓龙．最大相关峭度解卷积结合1.5维谱的滚动轴承早期故障特征提取方法[J]．振动与冲击，2015，34(12): 79-84.

TANG Guiji，WANG Xiaolong．Feature extraction for rolling bearing incipient fault based on maximum correlated kurtosis deconvolution and 1.5 dimension spectrum[J]. Journal of Vibration and Shock，2015，34(12): 79-84.

[3] 钟先友，赵春华，陈保家，等．基于MCKD和重分配小波尺度谱的旋转机械复合故障诊断研究[J]．振动与冲击，2015，34(7): 156-161.

ZHONG Xianyou，ZHAO Chunhua，CHEN Baojia，et al．Rotating machinery fault diagnosis based on maximum correlation kurtosis deconvolution and reassigned wavelet scalogram[J]．Journal of Vibration and Shock，2015，34(7): 156-161.

[4] HUANG N E，SHEN Z，LONG S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]．Proceedings of the Royal Society of London，1998，454(1971): 903-995.

[5] DRAGOMIRETSKIY K，ZOSSO D．Variational mode decomposition[J]．IEEE Transaction on Signal Processing，2014，62(3): 531-544.

[6] LIU Y Y，YANG G L，LI M，et al．Variational mode decomposition denoising combined the detrended fluctuation analysis[J]. Signal Processing，2016，125: 349-364.

[7] WANG X D，ZI Y Y，HE Z J．Multiwavelet construction via an adaptive symmetric lifting scheme and its applications for rotating machinery fault diagnosis[J]. Measurement Science and Technology，2009，20(4): 1-17.

[8] SMITH W A，RANDALL R B．Rolling element bearing diagnostics using the Case Western Reserve University data：a benchmark study[J]．Mechanical Systems and Signal Processing，2015，64: 100-131.

FeatureextractionforrollingelementbearingweakfaultbasedonMCKDandVMD

XIA Junzhong, ZHAO Lei, BAI Yunchuan, YU Mingqi, WANG Zhi’an

(Research Center of Military Vehicle Engineering & Technology，Academy of Military Transportation，Tianjin 300161，China)

The fault feature of rolling element bearings in early failure period is so weak and susceptible to random noise and other signal interferences that it is very difficult to be extracted. To solve this problem, the maximum correlated kurtosis deconvolution was combined with the variational mode decomposition for extracting rolling element bearing fault feature. Firstly the signal was enhanced by MCKD and decomposed into several modes by VMD. The signal then was reconstructed and noise was reduced with the mode，which was selected by the comparative correlation coefficient and the kurtosis criterion. Fnally the envelope demodulation was used to extract fault feature. The simulating signal analysis and bearing fault simulator show the validity of the method. This method can accurately separate different frequency components of bearing fault vibration signals.

rolling element bearing；maximum correlated kurtosis deconvolution(MCKD)；variational mode decomposition(VMD)；correlation coefficient；kurtosis criterion

2016-04-07 修改稿收到日期： 2016-08-21

夏均忠 男，博士，教授，1967年生

赵磊 男，研究生，1991年生

E-mail:1016091436@qq.com

TH133.33

A

10.13465/j.cnki.jvs.2017.20.013