长杆弹超高速侵彻半无限靶理论模型的对比分析与讨论

孔祥振， 方 秦， 吴 昊， 龚自明

(解放军理工大学 国防工程学院 爆炸冲击防灾减灾国家重点实验室，南京 210007)

长杆弹超高速侵彻半无限靶理论模型的对比分析与讨论

孔祥振， 方 秦， 吴 昊， 龚自明

(解放军理工大学 国防工程学院 爆炸冲击防灾减灾国家重点实验室，南京 210007)

分别基于六组典型长杆弹超高速侵彻金属靶体以及三组长杆弹侵蚀侵彻混凝土靶体的实验数据，对经典一维AT模型及其五个改进模型对弹体侵彻深度的预测能力进行了评估，并讨论了靶体等效强度(Rt)变化以及弹体的轴线速度变化。计算结果表明，对于长杆弹高速侵彻金属靶体的分析计算，应首选AW模型，其次为LW模型。而对于混凝土靶体，已有有限的实验数据表明，上述六个模型对于长杆弹侵蚀侵彻混凝土靶体侵彻深度预测均不适用，其主要原因在于Rt不能反映超高速侵彻下混凝土靶体的响应。最后基于分析结果，给出了长杆弹侵蚀侵彻混凝土靶体进一步的研究方向。

高速侵彻；理论模型；侵彻深度；混凝土

长杆高速穿甲弹是目前各国普遍采用的反坦克、装甲车、舰艇和附有装甲工事的主要武器之一。它具有硬度高、速度快、长细比大等特点，对攻击目标的侵彻能力远远地超过了旧式穿甲弹。简化的分析模型对于进一步发展和积极防御该弹种都有重要的意义。高速冲击下，弹靶材料发生复杂的变形和破坏，且弹靶间压力远高于材料强度，弹靶可近似作为流体处理。基于实验观察，Eichelberger等[1]提出了长杆弹高速侵彻半无限靶的四个阶段，即：初始瞬态阶段、准定常侵彻阶段、惯性扩展阶段和弹性恢复阶段，其中，初始瞬态阶段和弹性恢复阶段贡献较小，可忽略不计，而准定常阶段占主导地位，是研究的热点和重点。

基于Bernoulli方程，Tate[2-3]和Alekseevskii[4]各自独立提出了修正的流体动力学一维模型(AT模型)，成为研究长杆弹高速侵彻的基础理论。在过去的几十年中，AT模型广泛应用于工程设计(如弹体和防护材料的优化)。近年来，基于AT模型，诸多学者提出了改进的理论模型。孙庚辰等[5]基于对坑底材料的流动分析，提出了新的轴向应力平衡方程，建立了长杆弹垂直侵彻半无限厚靶板的简化模型(SWZS模型)；并进行了合金钢弹侵彻装甲钢的实验，将理论预测值和实测侵彻深度进行了对比分析。Rosenberg等[6]考虑到实际侵彻过程中长杆弹蘑菇头中心到边缘受力的不均匀性，通过引入等效截面积改进了Bernoulli方程，提出了RMM模型。Walker等[7]基于二维数值模拟结果，通过假设侵彻过程中应力场和速度场分布，并利用柱形空腔膨胀理论得到靶体阻力和瞬时侵彻速度的关系，进一步修正了AT模型，提出了AW模型。Zhang等[8]基于空腔膨胀理论，并假设长杆弹头部为半球形，得到了弹靶交界面的平均压力，并通过引入孔洞直径和长杆弹直径修正了轴向应力平衡方程，提出了ZH模型。Lan等[9]利用与空腔膨胀理论相似的方法，在靶体中定义不同的响应分区，并通过假设靶体中速度场分布，改进了Bernoulli方程，提出了LW模型。同时，也有学者另辟蹊径，提出了新的长杆弹高速侵彻半无限靶模型，如Grace[10]提出的“有限质量”模型，Rubin等[11-12]提出的速度势分析模型，Jones等[13]提出的“工程应变”模型等。

然而，各模型均采用较少的实验数据进行对比分析，且各模型对于弹靶性能参数的取值也不统一，各模型的预测能力值得商榷，因此有必要对各模型进行评估，给出使用建议。楼建峰[14]对六个分析模型进行了探讨并讨论了弹靶性能参数对侵彻深度的敏感性，但其只选取了Silsby[15]一组实验数据，且各模型靶体阻力Rt均取为Tate形式[16]，与原模型相悖，并且未考虑惯性扩展阶段的贡献。

另外，新型高强合金材料和推进技术的发展以及防护工程的日益深地下化和坚固化，促使钻地弹打击速度越来越高，因此，长杆弹侵蚀侵彻混凝土靶体的终点弹道效应研究引起了广泛关注[17-22]。然而，上述模型均针对金属靶体提出，能否推广应用于混凝土等脆性材料靶体尚不明确。

本文在简要介绍AT模型及其改进模型的基础上(对“有限质量”、“速度势”和“工程应变”模型不做进一步讨论)，基于Anderson等[23]六组典型长杆弹打击金属靶实验数据，从靶体阻力变化、速度(v和u)时程曲线及侵彻深度等方面，对各模型进行了评估，并给出使用建议。另外，基于已有有限的长杆弹侵蚀侵彻混凝土靶体实验数据，探讨了各模型对于混凝土靶体的适用性，并给出了进一步研究的方向。

1 长杆弹高速侵彻半无限靶的理论模型

本节简要介绍AT模型及其改进模型，各模型的具体推导过程在相关文献中已有详细说明，这里不再赘述，只给出控制方程和求解方法。

1.1AT模型

假设准定常侵彻过程中，长杆头部较小区域和弹靶交界面附近靶体处于流体状态，长杆尾部为刚体，基于Bernoulli方程，Tate和Alekseevskii各自独立提出了修正的流体动力学一维模型(AT模型)，如图1所示。

弹靶交界面轴向应力平衡方程

ρp=(v-u)2/2+Yp=ρtu2/2+Rt

(1)

杆长变化方程

(2)

弹体减速运动方程

(3)

侵彻方程

(4)

(5)

式中：σyp和σyt分别为弹靶动态屈服强度；Et为靶体弹性模量；λ为经验常数，通常取为0.7。根据Yp和Rt的相对大小，存在以下两种情况：

图1 侵彻模型示意图Fig.1 Diagram of penetration model

1.2SWZS模型

孙庚辰等基于对坑底流动区的分析，改进了弹靶交界面轴向应力平衡方程，即

2ρp(v-u)2+Yp=3ρtu2+2Rt

(6)

式中：Yp取为弹体材料的极限拉伸强度；Rt取为空腔在不可压缩线性硬化材料中膨胀时的表面压力并由下式确定

(7)

式中：E2为硬化模量。杆长变化方程，弹体减速运动方程和侵彻方程同AT模型。类似的，根据Yp和Rt的相对大小，存在以下两种情况：

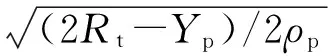
1.3RMM模型

Rosenberg等考虑到实际侵彻过程中长杆弹蘑菇头中心到边缘受力的不均匀性，通过引入等效截面积改进了Bernoulli方程，即：

(8)

式中：Ap和At分别为长杆弹刚性部分和蘑菇头的等效面积，Rosenberg等建议取At/Ap=2；Yp取为弹体材料Hugoniot弹性极限，Yp=σyp(1-v)/(1-2v)，v为泊松比；Rt取为柱腔膨胀得到的阻力函数，

(9)

杆长变化方程，弹体减速运动方程和侵彻方程同AT模型，即式(2)～式(4)。同样，根据Yp和Rt的相对大小，存在以下两种情况：

1.4AW模型

基于对二维数值模拟结果的分析，通过假设侵彻过程中速度场和应力场分布，Walker和Anderson建立了长杆弹垂直侵彻半无限厚靶板的分析模型。

弹靶交界面轴向应力平衡方程为

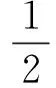
(10)

式中：α为靶体中塑性区无量纲化长度，由可压缩材料的柱腔膨胀模型得到

(11)

1.5ZH模型

假设长杆侵彻过程中，长杆头部形状为半球形，Zhang和Huang修正了弹靶交界面轴向应力平衡方程

(12)

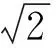
根据Yp和Rt的相对大小，存在以下两种情况：

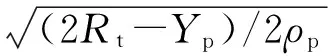
1.6LW模型

基于与空腔膨胀相似的方法，通过在靶体中定义不同的响应分区，并假设靶体中速度场分布，Lan和Wen改进了Bernoulli方程

(13)

(14)

式中：n为可调系数，本文计算取为2.45。式(13)联合杆长变化方程(式(2))，弹体减速运动方程(式(3))和侵彻方程(式(4))构成了LW模型。

1.7 模型的求解

本文对于上述六个模型，均采用数值方法求解。在t时步，首先由刚体部分速度vt，并根据轴向应力平衡方程(式(1)、(6)、(8)、(12)、(13))得到瞬时侵彻速度ut，然后利用四阶龙哥库塔算法求解由杆长变化方程(式(2))、弹体减速运动方程(式(3))和侵彻方程(式(4))构成的常微分方程组，从而得到t+1时步的杆长lt+1、刚体部分速度vt+1和瞬时侵彻深度Pt+1，然后进入下一时步的计算，直至u≤0或l≤0，终止计算。

1.8 惯性扩展阶段

上述介绍了各模型准定常侵彻阶段的计算方法，对于惯性扩展阶段，本文对各模型均按Tate提出的经验公式计算，

(15)

图2 模型求解流程图Fig. 2 Flow chart of the solving procedure

式中：u0为与打击速度v0对应的侵彻速度，Rs=2σyt/3[1+ln(2Et/3σyt)]，Dc为开坑直径，由下式计算，

(16)

式中：D为弹体初始直径。最终侵彻深度由准定常阶段和惯性扩展阶段相加得到。

2 各个模型计算结果的对比分析

为便于比较分析，将上述六种模型的轴向应力平衡方程(式(1)、(6)、(8)、(10)、(12)、(13))均写为AT模型的形式，即ρp(v-u)2/2+[Yp]=ρtu2/2+[Rt]，表1分别给出了各模型的[Yp]和[Rt]的表达式。

由表1可以看出，各模型的[Yp]和[Rt]的表达式差别非常大，因此，有必要对上述几个模型进行分析评价并给出建议。本节分别从[Rt]变化趋势，轴线速度(v和u)时程曲线、打击金属靶体侵彻深度三个方面，详细评价分析各模型的优劣。另外，基于三组长杆弹侵蚀侵彻混凝土靶体的实验数据探讨了六个模型对于高速侵彻混凝土靶体的适用性，并给出长杆弹高速侵彻混凝土靶体进一步研究的方向。

表1 各模型的[Yp]和[Rt]的表达式Tab.1 [Yp] and [Rt] expressions of each model

2.1 [Rt]随弹体速度变化

图3给出了各模型无量纲化的靶体等效强度[Rt]/[Rt]AT随弹体速度的变化趋势，其中[Rt]AT为AT模型计算得到的靶体等效强度，由式(5)给出，弹体为钨合金，靶体为装甲钢(布氏硬度为BHN295)，弹靶材料参数如表2所示。

图3 各模型无量纲化的随弹体速度的变化Fig.3 Dimensionlessversus projectile velocity for each model

由图3可以看出，AT模型的靶体等效强度[Rt]为常数；RMM和SWZS模型的[Rt]随弹体速度增大而增大；ZH模型的[Rt]虽然随着弹体速度增大而减小，但速度较高时[Rt]小于零，与实际情况不符；AW模型的[Rt]随弹体速度增大而减小；而LW模型[Rt]随弹体速度增大先减小后增大。

Anderson等[25]基于对实验数据的反向拟合得到，[Rt]依赖于弹体速度，并随着弹体速度的增大而减小。上述六个模型只有AW模型准确地反应出了这一现象。

2.2 弹靶轴线速度变化

由第二节模型介绍可知，只有AW模型考虑了初始侵彻时的瞬态阶段。图4分别给出了AT模型、AW模型和LW模型轴线速度(即v和u)随瞬时侵彻深度的变化曲线，其中，弹靶分别为钨合金和装甲钢(布氏硬度为BHN295)，初始打击速度为1 800 m/s。

由图4可见，AW模型较好地考虑到了初始撞击的瞬态阶段，与Eichelberger和Gehring的实验观测结果和Anderson等[26]的数值模拟结果较为吻合，而其余模型均未考虑到初始瞬态阶段的影响。

表2 弹靶性能参数Tab.2 Property parameters of projectiles and rods

图4 各模型轴线速度随瞬时侵深的变化Fig.4 Axial velocities versus depth of penetration for each model

2.3 金属靶体侵彻深度

本节选取Hohler和Stilp的六组典型实验数据进行对比分析，注意到该六组实验基本涵盖了所关心的弹靶材料和速度范围，弹靶材料性能参数如表2所示，

图5分别给出了六组弹体无量纲侵彻深度的实验数据和六个模型的预测曲线。

由图5可以看出：

(1)综合来看，AT和RMM模型低估了侵彻深度，而ZH模型高估了侵彻深度；SWZS模型在速度较低时高估侵彻深度，而在速度较高时低估了侵彻深度。AW模型和LW模型在整个速度域内与实验数据吻合较好。

(2)当撞击速度非常高，例如高速射流侵彻靶板时，可以忽略弹靶强度，各模型轴向力平衡方程应退化为Bernoulli方程ρp(v-u)2/2=ρtu2/2，但由式(6)、式(8)和式(12)可以看出，SWZS、RMM和ZH模型均不能退化为Bernoulli方程，这应是这三个模型不能较好预测侵彻深度的原因之一。

图5 各模型预测侵彻深度及与实验数据的对比Fig. 5 Comparisons of normalized depth of penetration between each model and experiment data

(3)由2.1节的讨论可知，AT、RMM和SWZS模型的靶体等效强度[Rt]均未反映出随弹体速度增大而减小的趋势，ZH模型的[Rt]虽然随着弹体速度增大而减小，但速度较高[Rt]<0时，与实际情况不符。不能准确地反映出[Rt]的变化趋势应可能是上述四个模型不能较好地预测侵彻深度的原因之一。

(4)由2.2节讨论可知，只有AW模型考虑到了初始瞬态阶段，与实验观测结果和二维数值模拟结果相一致，其它五个模型均未考虑到瞬态阶段的影响。

(5)值得注意的是，对于侵彻深度预测较好的AW和LW模型均利用了动态空腔膨胀模型或类似的思想和方法，因此，进一步的改进模型或提出新模型宜考虑利用动态空腔膨胀理论或类似的思想。

(6)综合上述分析，对于长杆弹高速侵彻金属靶体的分析计算，建议首选AW模型，其次为LW模型。

2.4 混凝土靶体侵彻深度

上述六个模型均针对金属靶体提出，能否推广应用于混凝土靶体尚不明确，本节基于已有公开发表的长杆弹侵蚀侵彻半无限混凝土靶体的有限实验数据，探讨上述六个模型对混凝土靶体的适用性。弹靶材料性能参数如表2所示，图6分别给出了三组实验数据和六个模型预测曲线。

图6 各模型预测侵彻深度及与实验数据的对比Fig. 6 Comparisons of normalized depth of penetration between each model and experiment data

由图6可见：

(1)对于实验1，ZH模型与实验最为接近，但由于实验数据较少，不能由此判断ZH模型适用于混凝土靶体；而对于实验2和3，各模型与实验吻合均不好。

(3)图6(d)分别给出了AT和AW模型对39 MPa和51.9 MPa混凝土的预测曲线，可以看出，在速度较小时(AT模型800 m/s左右，AW模型900 m/s左右)，两个模型计算得到的51.9 MPa混凝土靶体侵彻深度大于39 MPa混凝土侵彻深度，也就是说在速度较小时，两个模型预测的51.9 MPa混凝土靶体抗侵彻能力劣于39 MPa混凝土靶体(其他四个模型同样存在该现象)，这显然与实验数据相悖，原因应有以下两个：①高速冲击下混凝土产生破碎流动，与金属靶体响应有较大差别，因此，上述六个模型的靶体等效强度Rt均不能直接推广应用于混凝土靶体；②计算中未考虑刚性侵彻部分的影响。基于静态球形空腔膨胀理论，采用三段式状态方程和考虑拉伸和剪切破坏的屈服准则描述混凝土，李志康和黄风雷给出了高速侵彻下混凝土靶体等效强度Rt的表达式，然而，其计算得到的Rt为常数，不能反映出侵彻过程中Rt随侵彻速度u的关系。

(4)Nia等通过对实验2和实验3的分析表明，对于长杆弹侵蚀侵彻混凝土靶体，经典的刚性弹侵彻混凝土靶体的Forrestal公式[27]将过高估计侵彻深度，而利用流体动力学方程得到的侵彻深度与实验偏差也较大，上述分析表明已有的六个长杆弹高速侵彻模型也不适用于混凝土靶体，因此，长杆弹侵蚀侵彻混凝土靶体的理论模型需要进一步研究。

(5)已有对长杆弹侵蚀侵彻混凝土靶体的终点弹道效应的实验研究十分匮乏，仍需要进一步的实验工作。

综上，六个模型对于长杆弹侵蚀侵彻混凝土靶体均不适用，建议进一步工作从以下三个方面展开：①实验研究；②提出适用于混凝土靶体等效强度Rt公式，Rt应同时计及混凝土材料性能和侵彻速度u的影响；③临界速度Vr和刚性侵彻部分的研究。

3 结 论

基于六组典型长杆弹打击金属靶体和三组长杆弹侵蚀侵彻混凝土靶体的实验数据，本文从靶体等效强度变化、弹体的轴线速度变化以及侵彻深度三个方面，对六个长杆弹高速侵彻半无限金属靶体模型进行了分析讨论和评价，并探讨了六个模型对于高速侵彻混凝土靶体的适用性。主要结论有：

(1)对于长杆弹高速侵彻金属靶体，计算结果表明，AW模型的[Rt]随弹体速度增大而减小，且较好地考虑到了初始撞击的瞬态阶段，侵彻深度与实验吻合较好，LW模型计算得到的侵彻深度与实验吻合也较好，因此建议首选AW模型，其次为LW模型。

(2)对于长杆弹侵蚀侵彻混凝土靶体，计算结果表明六个模型均不适用，其主要原因是，基于金属靶体的长杆弹侵蚀侵彻的理论模型不能有效地反映高速冲击混凝土靶体的作用机理。

(3)对于长杆弹侵蚀侵彻混凝土靶体的理论模型的建立仍需大量的研究工作，建议应加强以下三个方向的研究：①实验研究；②提出适用于混凝土靶体等效强度Rt公式，Rt应同时计及混凝土材料性能和侵彻速度u的影响；③临界速度Vr刚性侵彻部分的研究。

[1] EICHELBERGER R J, GEHRING J W. Effects of meteoroid impacts on space vehicles [J]. ARS Journal, 1962, 32(10): 1583-1591.

[2] TATE A. A theory for the deceleration of long rods after impact [J]. Journal of the Mechanics and Physics of Solids, 1967, 15(6): 387-399.

[3] TATE A. Further results in the theory of long rod penetration [J]. Journal of the Mechanics and Physics of Solids, 1969, 17(3): 141-150.

[4] ALEKSEEVSKII V P. Penetration of a rod into a target at high velocity [J]. Combustion, Explosion, and Shock Waves, 1966, 2(2): 63-66.

[5] 孙庚辰, 吴锦云, 赵国志, 等. 长杆弹垂直侵彻半无限厚靶板的简化模型 [J]. 兵工学报, 1981, 4: 1-8.

SUN Gengchen, WU Jinyun, ZHAO Guozhi, et al. A simplified model of the penetration of the long- rod penetrator against the plates with semi-infinite thickness at normal angle [J]. Acta Armamentarii, 1981, 4: 1-8.

[6] ROSENBERG Z, MARMOR E, MAYSELESS M. On the hydrodynamic theory of long-rod penetration [J]. International Journal of Impact Engineering, 1990, 10(1): 483-486.

[7] WALKER J D, ANDERSON Jr C E. A time-dependent model for long-rod penetration [J]. International Journal of Impact Engineering, 1995, 16(1): 19-48.

[8] ZHANG L S, HUANG F L. Model for long-rod penetration into semi-infinite targets [J]. Journal of Beijing Institute of Technology, 2004, 13(3): 285-289.

[9] LAN B, WEN H M. Alekseevskii-Tate revisited: An extension to the modified hydrodynamic theory of long rod penetration [J]. Science China Technological Sciences, 2010, 53(5): 1364-1373.

[10] GRACE F I. Non steady penetration of longs rods into semi-infinite targets [J]. International Journal of Impact Engineering, 1993, 14(1): 303-314.

[11] RUBIN M B, YARIN A L. On the relationship between phenomenological models for elastic-viscoplastic metals and polymeric liquids [J]. Journal of Non-newtonian Fluid Mechanics, 1993, 50(1): 79-88.

[12] RUBIN M B, YARIN A L. A generalized formula for the penetration depth of a deformable projectile [J]. International Journal of Impact Engineering, 2002, 27(4): 387-398.

[13] JONES S E, GILLIS P P, FOSTER Jr J C. On the penetration of semi-infinite targets by long rods [J]. Journal of the Mechanics and Physics of Solids, 1987, 35(1): 121-131.

[14] 楼建锋. 侵彻半无限厚靶的理论模型与数值模拟研究 [D]. 绵阳：中国工程物理研究院, 2012.

[15] SILSBY G F. Penetration of semi-infinite steel targets by tungsten long rods at 1.3 to 4.5 km/s [C] //8th Int Symp Ballistics. Orlando, FL, 1984.

[16] TATE A. Long rod penetration models—Part II. Extensions to the hydrodynamic theory of penetration [J]. International Journal of Mechanical Sciences, 1986, 28(9): 599-612.

[17] GOLD V M, VRADIS G C, PEARSON J C. Concrete penetration by eroding projectiles: experiments and analysis [J]. Journal of Engineering Mechanics, 1996, 122(2):

145-152.

[18] GOLD V M, VRADIS G C. Analysis of penetration resistance of concrete [J]. Journal of Engineering Mechanics, 1998, 124(3): 328-338.

[19] NIA A A, ZOLFAGHARI M, MAHMOUDI A H, et al. Analysis of resistance of concrete target against penetration of eroding long rod projectile regarding flow field around the projectile tip [J]. International Journal of Impact Engineering, 2013, 57: 36-42.

[20] NIA A A, ZOLFAGHARI M, KHODARAHMI H, et al. High velocity penetration of concrete targets with eroding long-rod projectiles; an experiment and analysis [J]. International Journal of Protective Structures, 2014, 5(1): 47-64.

[21] 练兵, 蒋建伟, 樊虎, 等. 高速长杆弹侵彻半无限混凝土靶深度分析模型 [J]. 弹箭与制导学报, 2011, 31(1): 85-

87.

LIAN Bing, JIANG Jianwei, FAN Hu, et al. Depth analysis model of penetration of high speed projectiles into semi-infinite concrete [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(1): 85-87.

[22] 李志康, 黄风雷. 高速长杆弹侵彻半无限混凝土靶的理论分析 [J]. 北京理工大学学报, 2010 (1): 10-13.

LI Zhikang, HUANG Fenglei. High velocity long rod projectile’s penetration into semi-infinite concrete target [J]. Transactions of Beijing Institute of Technology, 2010 (1):

10-13.

[23] HOHLER V, STILP A J. A penetration mechanics database [R]. San Antonio, TX: Southwest Research Institute, 1992.

[24] HILL R. The mathematical theory of plasticity [M]. Oxford: Oxford University Press, 1998.

[25] ANDERSON Jr C E, WALKER J D, HAUVER G E. Target resistance for long-rod penetration into semi-infinite targets [J]. Nuclear Engineering and Design, 1992, 138(1): 93-104.

[26] ANDERSON Jr C E, WALKER J D. An examination of long-rod penetration [J]. International Journal of Impact Engineering, 1991, 11(4): 481-501.

[27] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395-405.

Comparisonsoflongrodhighvelocitypenetrationmodelsforsemi-infinitetargets

KONG Xiangzhen, FANG Qin, WU Hao, GONG Ziming

(State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, College of National Defense Engineering, PLA University of Science and Technology, Nanjing 210007, China)

Based on four typical metal penetration and three concrete penetration experimental data, the predication performance for depth of penetration of six theoretical models were analyzed and evaluated, respectively. The target resistance (Rt) and the time history curve of axial velocity were discussed. The calculation results indicated that the AW model is the best for long rod projectile penetrating into metal targets. However, calculation results showed that none of the six penetration models are suitable for the concrete target, mainly due to the difference of response between metal and concrete targets under high velocity impact. In addition, further research interest on the hypersonic velocity penetration of concrete target was proposed.

high velocity penetration; theoretical model; depth of penetration; concrete

国家自然科学基金创新研究群体科学基金(51321064)；国家自然科学基金优秀青年基金(51522813)

2016-05-04 修改稿收到日期： 2016-07-08

孔祥振 男，博士生，1988年生

方秦 男，教授，博士生导师，1962年生

TJ012

A

10.13465/j.cnki.jvs.2017.20.007