基于DSMC方法的高空固发羽流模拟

丁逸夫，赵 瑜，王平阳

(1.上海交通大学 机械与动力工程学院,上海 200240； 2.上海航天化工应用研究所,上海 201109)

基于DSMC方法的高空固发羽流模拟

丁逸夫1，赵 瑜2，王平阳1

(1.上海交通大学 机械与动力工程学院,上海 200240； 2.上海航天化工应用研究所,上海 201109)

为研究稀薄状态下固体火箭发动机羽流中颗粒的行为，在稀薄气相流场DSMC程序的基础上，添加了气固两相相互作用模型和颗粒相变模型。气固两相相互作用模型中，颗粒所受的作用由单个颗粒受到周围分子力和热作用公式求出，分子所受的作用由耦合求解气固相互作用方法求出，颗粒相变考虑固化、熔解，以及不发生相变的加热与冷却。用算例研究了流场的特性参数及不同粒径颗粒的温度分布，与文献数据符合良好，准确度在国内同类研究中具有一定的优势。在此基础上，针对实际固发羽流算例进行计算，分析了不同颗粒直径对流场的影响。结果表明：粒径越小颗粒扩散越开，X=0.4 m处粒径1 μm颗粒的扩散较粒径100 μm从0.03 m增大到0.2 m；粒径越小颗粒温度降低越多，X=0.4 m处近轴线位置粒径1 μm颗粒的温度较粒径100 μm降低了44.4%；粒径越大，对气相流场阻碍作用越明显，X=0.02 m处近轴线位置粒径100 μm颗粒的速度较纯气相流场降低了54.5%。

固体发动机； 高空羽流； 气固两相流； 相互作用模型； 颗粒相变模型； 流场特性参数； 温度分布； 颗粒直径； DSMC

0 引言

固体火箭发动机有悠久的历史和广泛的应用，在运载火箭的助推器和上面级、弹道导弹上面级、弹道导弹防御系统、飞行员紧急逃生装置中都有使用。高空环境固体火箭发动机羽流中，气体膨胀导致温度降低，颗粒温度明显高于周围气体，是羽流辐射的主要来源，一方面对航天器羽流可见区域产生一定的影响，另一方面羽流红外可见特性是导弹隐身和目标识别所关注的。同时，颗粒在卫星姿轨控、二级火箭分离时可能与下游航天器壁面发生碰撞，对其正常工作造成一定的危害。因此，关于固体火箭发动机的稀薄气固两相羽流场研究越来越受重视，对颗粒行为的模拟成为研究者关心的问题。

基于连续流假设的CFD方法无法准确模拟稀薄流场[1]。由BIRD提出的DSMC方法，经过多年的发展已成为求解稀薄流的重要方法。将DSMC方法直接用于高空固发羽流的模拟有一定的难度，主要表现在以下：颗粒相对分子几何尺寸很大，两者间发生的是多体碰撞；颗粒出口常呈熔融态，随流动发生复杂的相变过程；颗粒与分子间的碰撞传能计算；颗粒与周围环境的辐射换热计算等。国外对高空固发羽流的研究始于2000年，GALLIS推导出单个固体颗粒受周围气体分子作用力和热的模型[2]。在此基础上密歇根大学的BOYD和BURT等提出了耦合求解气固两相相互作用的技术路线，丰富完善了该模型[3-4]。国内的研究起步较晚，最早的相关报道是文献[5]采用GALLIS提出的模型求解气固两相力与热的相互作用，并初步论述了过程中动量和能量的传输机制。文献[6]用DSMC/EPSM混合算法结合气粒耦合作用模型，对羽流参数进行了模拟，但未考虑颗粒相变的影响。文献[7]通过坐标变换计算了含液相颗粒的羽流场，但同样未考虑相变。文献[8]计算了高空固发羽流，同样未考虑颗粒相变的影响。文献[9]在文献[5]的基础上添加了相变模型，模拟结果与BURT结果的趋势基本一致，但仍存在较明显的误差。相变会导致固体颗粒温度升高，并导致不考虑相变的羽流热效应偏低。本文在DSMC框架下耦合气固两相相互作用模型和颗粒相变模型，对高空固发羽流模拟进行了研究，对气体数密度和不同直径的颗粒温度等流场参数分别与文献[3，9]的结果进行比较。在此基础上，建立了一个固发模型，考察不同颗粒直径对流场参数的影响规律，以及颗粒的温度与密度分布，为后续耦合辐射模型研究固发羽流对敏感表面的影响提供参考。

1 数学模型

对液发羽流纯气相流场的研究中使用DSMC方法求解已积累了大量经验[10]。本文重点是与固发羽流模拟特有的颗粒相关的原理和模型。

1.1气相对固相的作用

根据GALLIS提出的单个固体颗粒受到周围气体分子作用力和热的模型，设同一个网格中，每个气体仿真分子作用到某个固体颗粒上的力、力矩、热量分别为FP，MP，QP，有

FP=FPnr+FPot

(1)

(2)

(3)

(4)

QP=π(RP)2×

(5)

式中：Ur为分子对颗粒的相对速度；Rp为等效颗粒半径；Ng为仿真分子权因子；Vc为网格体积；m为单个真实气体分子的质量；Cr为气体分子相对固体颗粒的速度的模；τ为固体颗粒的表面热适应系数；kB为波尔兹曼常数；Tp为固体颗粒的温度；ωp为固体颗粒的转动角速度；θ为气体分子转动自由度；er为单个真实气体分子的平均转动能[2]。对每个颗粒，令其与对应网格的分子发生碰撞，效果累加且作用于颗粒，得下一时刻固体颗粒的速度、角速度和温度。

1.2固相对气相力和热的作用

考虑固相对气相的影响，需选取与颗粒发生碰撞的分子。根据BIRD提出的非时间计数器方法(NTC)，先确定所有可能发生碰撞的网格中仿真分子数N，再计算碰撞概率，由颗粒以Cr以对应时间步长扫过的体积与网格体积之比决定。两者相乘得到与颗粒发生碰撞的分子数Ns，有

Ns=floor(WpNπ(Rp)2(Cr)maxΔt/Vc+R)

(6)

式中：Wp为颗粒权因子；R为0～1随机数；floor表示向下取整；Δt为时间步长。选取时根据接受拒绝法，生成0～1的随机数，与每个分子Cr/(Cr)max比较，Cr/(Cr)max较大时认为该分子与颗粒发生碰撞。

与该颗粒发生碰撞的仿真分子，一部分以概率τ发生漫反射，另一部分以概率1-τ发生镜面反射。镜面反射不改变分子的温度，相对速度大小在碰撞中亦不变。漫反射分子与颗粒充分交换热量，分子以颗粒温度为热速度反射出去。漫反射分子反射后相对速度的概率分布可表示为

(7)

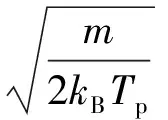
(8)

1.3固体颗粒相变模型

颗粒的相变在固发羽流中十分常见，不仅影响自身的温度，而且对周围气体分子状态产生影响。熔融态Al2O3颗粒在流场中与周围分子相互作用温度降低，到达向α相Al2O3转变的温度(1 950 K)时发生相变，结晶由表面不断向内核发展，同时伴随有强烈的放热过程，温度升高至α相Al2O3向熔融态Al2O3转变的温度(2 330 K)时达到平衡。此时温度不变，颗粒对外散热与相变产生的热量平衡，结晶锋面不断向核心发展。

假设当颗粒温度显著低于熔点温度Tm达到结晶温度Tf时，颗粒由外向内发生相变，且一旦开始结晶表面不断向内发展，结晶锋面位置取决于

(9)

式中：r1为结晶锋面半径相对颗粒半径的值；t为时间；AC=2.7×10-6ms-1·K-1.8；nc=1.8[11]。

r1通过能量平衡方程对颗粒温度产生影响，可表示为

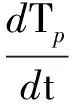
(10)

式中：CS为颗粒的比热容，且CS=1 225 J/(kg·K)；mp为颗粒质量；hf为相变潜热，且hf=1.07×106J/kg。

为描述颗粒相变过程，将颗粒相变分为三种独立情况：固化、熔解、不发生相变的加热和冷却。以下给出三种情况的判断依据，在此基础上阐述三种情况下锋面半径与传递热量的关系建立。

如Tp

(11)

式中：Δ(r1)3为(r1)3在时间Δt内的变化量。

如Tp≥Tm，r1<1，QP>0，颗粒将发生熔解。此时假设颗粒温度保持定值，传入颗粒的能量全部用于颗粒相变。令式(11)中颗粒温度变化值为零，计算出r1的值。特别地，如r1的值大于1，表明该热量全部用于相变仍有结余，此时将r1归1，颗粒温度变化可表示为

ΔTp=[hf/CS]((r1)3-1)

(12)

颗粒不发生相变，传入或传出颗粒的能量令颗粒温度升高或降低，颗粒温度变化可表示为

ΔTp=QPΔt/(CSmp)

(13)

2 验证算例

国内外关于高空固发羽流的实验很少，主要集中于对其宏观辐射的测量，关于流场颗粒的测量未见相关报道，计算无法直接与实验结果进行对比。为验证模型的正确，与国外文献[3]和相同算例国内文献[9]的计算结果进行比较。

2.1边界条件

边界条件如图1所示。验证算例为轴对称结构，对称轴为X轴，对称面为长80 m(-10 m到70 m)、宽30 m(0 m到30 m)的矩形。左边界为环境来流面，来流组成为摩尔分数78%的N2和摩尔分数22%的O2，温度288 K，马赫数13.5，密度5.79×10-8kg/m3。在局部放大图中可清晰看到喷管的结构，因原实验中为给出喷管结构的具体参数，本文对照原文近似了一个喷管结构，长3.1 m，出口直径0.78 m，圆柱段长1 m，喉部直径0.2 m。喷管壁面均为表面温度为300 K的漫反射面。

喷管出口为主要来流面，包含H2(摩尔分数0.38)、N2(摩尔分数0.31)和CO(摩尔分数0.31)三种组分的气体，温度1 433 K，速度3 113 m/s，密度0.011 kg/m3。除这三种气体外，还包括固体颗粒Al2O3，其占喷管出口总质量流量的30%，按粒径大小分为7组，直径为0.3～6 μm，颗粒基本参数见表1。

表1 固体颗粒(Al2O3)参数

2.2结果验证

气相主要流场参数分布如图2所示。由图2可知：分子流出喷管后迅速膨胀，沿+X、+Y向数密度迅速减小，膨胀的最大角度约45°。这条线将计算区域分为两部分：左侧为环境来流区域，右侧为高空固发羽流区域。在羽流区域，压力急剧降低，由于环境分子稀薄，对羽流阻碍较小，分子的内能转化为动能，静温降低，X、Y向速度均有显著增加。环境来流区域，初始来流速度高，但数密度较低，与羽流区域相互作用，速度降低，压强升高，在45°线上形成一个高压区，动能转为内能，且此处的羽流速度亦有所降低，温度升高，在该位置出现一个高温区域。

分子密度计算结果与文献[3]的比较如图3所示。其中文献[3]给出了4个密度的等值线。由图3可知：计算结果的流场结构与参考文献较接近，表明本文计算结果较可信。

在计算区域中的(0 m，0.02 m)到(70 m，25 m)的线段上统计固体颗粒的温度信息，并与文献[3，9]比较。跟踪线上气相温度变化如图4所示。由图4可知：在跟踪线上气相温度迅速降低，然后逐渐趋于平缓。本文结果与文献[3]的结果较一致，最大误差小于60 K，此时相对误差小于10%。跟踪线上粒径0.4 μm颗粒温度变化如图5所示。粒径0.4 μm颗粒在喷管出口的温度1 634 K，随着流动与分子碰撞传能温度降低。由图5可知：粒径0.4 μm的颗粒温度与文献结果较一致，先迅速下降然后趋于平缓，最大误差小于100 K，此时相对误差小于15%。跟踪线上粒径4 μm颗粒温度变化如图6所示。粒径4 μm颗粒温度变化较大，初始时颗粒温度2 178 K，随着流动温度降低，0.4 m位置达到1 950 K，此时熔融Al2O3发生相变结晶。由于相变向外放热，加之相变开始温度1 950 K明显低于熔点2 330 K，颗粒温度迅速上升，接近2 330 K时相变产生的热量与颗粒和分子碰撞散发的热量平衡，颗粒温度保持稳定。由图6可知：粒径4 μm的颗粒温度与文献结果较一致，最大温差约100 K，此时相对误差约5%。综上，可认为本文的高空固发羽流计算结果较准确。

3 固发算例

对实际高空固发羽流算例进行计算，重点比较颗粒粒径对气相流场分布的影响，以及颗粒的空间与温度分布。因没有耦合辐射模型，计算时仅选取距离喷管0.5 m的区域，此时认为耦合辐射对结果影响可忽略。

3.1边界条件

计算中发动机为锥形喷管(如图7所示)，喷管入口半径6 mm，喉部半径4 mm，R1为半径1 mm外切圆，喷管出口半径8.4 mm，喉部至喷管入口的距离6 mm，至喷管出口的距离7.38 mm。设总温2 803 K，总压2.4 MPa，喉部静压1.341 5 MPa；混合气体的摩尔分数分别为H2O(0.238 0)、CO(0.131 2)、CO2(0.045 76)、H2(0.292 8)、N2(0.292 1)。取颗粒粒径分别为1，10，100 μm，质量流量均为0.0 172 kg/s。

先用CFD方法对喷管内部含颗粒的连续流流场进行计算，取出喷管出口流场参数，再用DSMC程序进行计算羽流的稀薄流流场。网格按等比级数划分，X向100网格，末网格与首网格之比为10；Y方向60网格，末网格与首网格之比为5。

3.2结果分析

计算所得3种粒径颗粒的数密度分布云图如图8所示。由图8可知：颗粒扩散程度随粒径增加而逐渐降低，X=0.5 m处粒径1，10，100 μm的颗粒分别扩散至0.2，0.1，0.03 m处。

X=0.4 m处颗粒密度分布如图9所示。由图9可知：当质量流量一定时，颗粒粒径越小扩散越开，密度也越低。X=0.4 m处颗粒温度分布云图如图10所示。由图10可知：颗粒温度随颗粒粒径减小而降低，大粒径100 μm颗粒温度降至2 700 K，同比减小3.7%(与燃烧室温度2 803 K比较，下同)；粒径10 μm颗粒温度降至2 400 K，同比减小14.4%；粒径1 μm颗粒温度降至1 500 K，同比减小46.5%。综合图9、10，分布相同时，颗粒温度越高对反流区辐射影响就越显著，此时粒径越大影响越明显；温度相同时，扩散越开，相当于辐射面积越大，对反流区辐射影响就越显著，此时粒径越小影响越明显。综上，具体对反流区辐射影响效果还需后续进一步分析才能得出。

X=0.02 m处分子速度分布云图如图11所示。由图11可知：颗粒对所在区域分子的运动起阻碍作用，且粒径越大阻碍越明显。近轴线处，不添加颗粒时，分子速度2 750 m/s，添加粒径100 μm颗粒后速度降至1 250 m/s，同比减小54.5%；添加粒径10 μm颗粒后速度降至1 770 m/s，同比减小35.6%；添加粒径1 μm颗粒后速度降至2 630 m/s，同比减小4.4%。颗粒越大出口的速度越慢，且越集中在轴线附近，对气体运动阻碍越明显。

4 结束语

本文基于DSMC框架下耦合气固相互作用模型和颗粒相变模型，对文献[3]中的算例进行了计算，并与文献[3，9]的结果进行比较。在粒径1，10，100 μm三种颗粒条件下，对小型锥形喷管固体火箭发动机羽流进行了计算，并分析了计算结果，得到结论如下：第一，将GALLIS单个颗粒受周围分子作用力和热模型用于固发羽流模拟，计算结果与文献符合良好，气相最大误差小于60 K，最大误差出现处相对误差小于10%，固相最大误差小于100 K，此时相对误差均小于15%。第二，追踪线上的小粒径(0.4 μm)颗粒，因未发生相变，加之气体分子碰撞传递热量，温度一直降低；大粒径(4 μm)颗粒，发生相变后表面温度迅速升高，因无耦合辐射，计算范围内温度维持在2 330 K(α相Al2O3向熔融态的转变温度)。第三，颗粒加入对反流区辐射影响取决于颗粒空间分布和温度分布，粒径越小扩散越大，X=0.4 m处粒径1 μm的扩散较100 μm颗粒从0.03 m增大至0.2 m，对辐射有促进作用(图9)，但同时温度降低更显著。X=0.4 m处近轴线位置粒径1 μm的温度较100 μm颗粒降低了44.4%，对辐射有抑制作用(图10)，但具体作用效果还需后续分析。第四，颗粒粒径越大，对流场分子运动的阻碍越明显(图11)，X=0.03 m处近轴线位置添加粒径100 μm颗粒流场的分子X向速度较纯气相流场降低了54.5%。国内外很少有关于高空固发羽流的实验，实验数据主要为羽流宏观辐射特性，开展高空固发羽流流场参数测量实验，为模拟工作提供数据支撑，是后续研究方向之一。为形成对高空固发羽流中颗粒行为的完整描述，还需在本文研究的基础上耦合辐射模型。与气体分子相比，颗粒相关模型中存在大量的简化假设，部分假设对结果有显著的影响(如Al2O3相变过程晶型转变)，后续将分析这些简化假设对计算结果的影响，完善颗粒相关模型。

[1] BIRD G A. Molecular gas dynamics[R]. NASA STI/Recon Technical Report A, 1976.

[2] GALLIS M A, TORCZYNSKI J R, RADER D J. An approach for simulating the transport of spherical particles in a rarefied gas flow via the direct simulation Monte Carlo method[J]. Physics of Fluids, 2001, 13(13): 3482-3492.

[3] BURT J M. Monte Carlo simulation of solid rocket exhaust plumes at high altitude[D]. Michigan: The University of Michigan, 2006.

[4] BURT J M, BOYD I D. High altitude plume simulations for a solid propellant rocket[J]. AIAA Journal, 2007, 45(12): 2872-2884.

[5] 李洁, 尹乐, 颜力. 稀薄流气粒两相耦合作用的热力学模型[J]. 国防科技大学学报, 2009, 31(3): 6-10.

[6] 张斌, 毛根旺, 胡松启, 等. 固体微推力器气粒两相羽流场的数值模拟[J]. 固体火箭技术, 2011, 34(3): 314-318.

[7] 何小英, 贺碧蛟, 蔡国飙. 直接模拟蒙特卡罗羽流模拟的两相作用模型[J]. 推进技术, 2011, 32(2): 214-219.

[8] 李中华, 李志辉, 彭傲平, 等. 一种稀薄两相流动的数值模拟方法[J]. 空气动力学学报, 2015, 33(2): 266-271.

[9] 刘英, 李洁, 胡建峰, 等. 多相稀薄流动中的颗粒相变研究[J]. 固体火箭技术, 2014, 37(3): 330-335.

[10] 刘腾, 王平阳, 包轶颖, 等. 高超声速稀薄流球面气动热工程计算公式的建立[J]. 导弹与航天运载技术, 2012(5): 32-38.

[11] PLASTININ Y, ANFIMOV N, BAULA G, et al. Modeling of aluminum oxide particle radiation in a solid propellant motor exhaust[C]∥ 31st Thermophysics Conference. [S. l.]: [n. l.], 1996: 1879.

SimulationofHighAltitudeSolidRocketPlumeBasedonDSMCMethod

DING Yi-fu1， ZHAO Yu2， WANG Ping-yang1

(1. School of Mechanical and Power Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Shanghai Space Propulsion Technology Research Institute, Shanghai 201109, China)

In order to study the behavior of particles in the solid plume in the rarefied state, the gas-solid two-phase interaction model and the particle phase transition model were added on the basis of DSMC program. In the gas-solid two-phase interaction model, the force and heat of the particles are obtained by using force and thermal effects of single particle subject to the surrounding molecular. The force and heat of the molecules are obtained by the method in the technical route for solving gas-solid interaction. The particle phase change is based on the model which includes solidification, liquating and heating and cooling without phase change. The characteristic parameters of the flow field and the temperature distribution of particles with different particle sizes were studied by one sample. The results were in good agreement with the literature data. The accuracy of the results in the same research in domestic has certain advantages. The calculation of a real solid-rocket plume was carried out, and the effect of different particle diameters on the flow field was analyzed. The results show that the smaller the particle size, the more the particles diffuse. The diffusion of particles with diameter 1 μm is changed from 0.03 m to 0.2 m atX=0.4 m compared with particles with diameter 100 μm. The smaller the particle size, the more the particle temperature decreased. The temperature of particles with diameter 1 μm is decreased by 44.4% atX=0.4 m near-axis position compared with particles with diameter 100 μm. The larger the particle size, the more obvious obstruction of molecular motion in the flow field. The molecularXvelocity is decreased by 54.5% atX=0.02 m near-axis position compared with the pure gas flow field.

solid rocket engine; plume; gas-solid two-phase flow; interaction model; particle phase transition model; characteristic parameter of flow field; temperature distruction; particle diameter; DSMC

1006-1630(2017)05-0110-07

2017-02-13；

2017-03-31

国家自然科学基金资助(50306013)；航天先进技术联合研究中心基金资助(USCAST2013-31)

丁逸夫(1992—)，男，硕士生，主要研究方向为固体火箭发动机羽流模拟。

V43

A

10.19328/j.cnki.1006-1630.2017.05.018