基于驱动谱耦合修正的多轴多激励随机振动试验算法研究

钟珂珂，陈章位，张小龙，曹雪峰

(1.上海航天精密机械研究所,上海 201600；2.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027)

基于驱动谱耦合修正的多轴多激励随机振动试验算法研究

钟珂珂1，陈章位2，张小龙1，曹雪峰1

(1.上海航天精密机械研究所,上海 201600；2.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027)

针对航天产品目前主流多轴多激励随机振动环境试验的跟踪精度与控制稳定性不佳问题，对基于驱动谱耦合修正优化的算法进行了研究。根据多轴随机试验的振动控制原理与方法，提出用比例均方根迭代修正与系统频响特性更新均衡调控的方式提高试验控制系统驱动谱的跟踪精度，给出了相应的控制策略：根据参考谱中各控制谱的相干系数选择修正方法，相干系数小于0.95时，用更新系统频响矩阵的方法实现对驱动谱的修正；相干系数大于0.95时，用修正参考谱下三角矩阵的方法实现对驱动信号的修正，以此不断减小控制偏差。两点两激励的仿真控制结果表明：各控制点自谱控制效果好，满足工程要求。建立两振动台对细长条试件进行振动试验，结果表明控制响应自功率谱和动态范围均满足工程试验要求。

多轴多激励； 随机振动； 均衡调控； 跟踪精度； 控制稳定性； 驱动谱； 耦合修正； 相干系数

0 引言

大量工程实践业已表明，振动环境试验是评估产品硬件在真实使用环境中可靠性的有效方法。为适应航天领域众多被试产品可靠性的定量评定，多轴多激励随机振动试验技术因其良好的应力分布、模态激发和信噪比逐渐成为复杂结构件、大型柔性结构及长杆件(导弹等)武器装备可靠性试验中不可替代的工程手段。对多点随机振动试验控制的研究始于20世纪90年代，文献[1]用参考谱与响应谱间误差修正驱动谱的差分算法，并将其用于系统研究；文献[2]用二次相位调制方法实现对非高斯随机振动试验的控制，并定量分析了时域随机化对非高斯随机信号的影响，由理论推导发现重叠系数与窗函数的不同选择会改变响应信号的峭度值，但需事先计算修正系数，这造成了功率谱控制与峭度控制间存在相互影响；文献[3]对传统控制算法进行了改进，在误差谱修正过程中引入了比例均方根修正算法，从而避免功率谱对角线上元素出现零或负值的情况，保证了系统的稳定性，但因其非对角线上的互谱控制是通过修正自谱的过程自行完成，这将对有严格互谱控制要求的振动试验造成不利。

在多轴随机振动试验控制过程中，传统前馈闭环控制策略都较少涉及实时修正频响函数矩阵估计及其逆的方法，同时优先修正驱动谱靠前的对角线元素，这样就会导致参考谱中靠前的自谱控制效果较好，而靠后的自谱控制相对较差[4]。进一步需指出的是，主流的迭代控制算法对某些频率点上出现的负值自谱用零代替，这样会影响控制系统的稳定性。为有效解决航天器结构件振动可靠性环境试验中多轴多激励控制算法单纯更新系统频响特性导致的跟踪精度与控制稳定性欠佳的问题，本文在全面分析控制系统功率谱修正机理并结合主流控制算法优缺点的基础上，对相应的控制算法优化策略进行了研究，提出采用偏相干残差法进行多点激励随机振动试验控制系统频响估计的方法，给出了用于多输入多输出系统频响矩阵估计的计算流程。偏相干残差法相对传统的频响矩阵估计方法计算量更小，非常适于多点激励振动试验等实时性要求较高的系统，同时它能提供更多输入输出间的相干信息，在保证控制系统稳定的基础上，加快了控制系统的收敛速度。在此基础上，将基于比例均方根修正方法的驱动信号实时修正与基于残差分析的频响函数估计矩阵更新结合，提出综合均衡调控的优化控制策略与算法，以实现系统频响辨识精度与控制稳定性的改善[5]。

1 多轴随机试验的振动控制原理与方法

多轴多激励振动试验系统可视作由振动台、试件、夹具、功率放大器、传感器和控制器等组成的多输入多输出线性时不变系统。以n个激励点、m个控制点为例，多点激励振动试验系统如图1所示。

每个驱动信号d(t)都对所有的控制信号c(t)产生影响，对驱动信号与控制信号间的关系式进行傅里叶变换以转换至频域，并写成矩阵形式

即

C(f)=H(f)D(f)

(1)

式中：C(f)为控制信号的谱向量；D(f)为驱动信号的谱向量；H(f)为控制信号与驱动信号间的频率响应函数阵[6]。

对典型的多轴随机振动，其中涉及的向量需转换为功率谱密度矩阵形式。设参考向量R(f)、驱动向量D(f)和控制向量C(f)的功率谱密度矩阵分别为GRR，GDD，GCC，省略变量f以简化形式表示。令振动试验系统的真实频响矩阵为H；试验测量估计的振动试验系统频响矩阵为A；根据估计的系统频响矩阵得到解耦补偿矩阵为Z，则有Z=A-1。由式(1)可得随机振动试验控制的驱动谱

GDD=ZGRRZH

(2)

式中：上标“H”表示复共轭转置。对驱动谱和参考谱分别作Cholesky矩阵分解，分解成上三角与下三角矩阵乘积的形式

GDD=DDH

(3)

GRR=LLH

(4)

式中：D，L分别为上三角与下三角矩阵[7]。

2 驱动谱耦合修正优化算法

振动试验控制目标是在振动台上再现用户规定的参考信号。为使系统的响应信号C(f)与参考信号R(f)在误差允许的范围内保持一致，需对系统进行解耦，并以此确定所需的驱动信号。由式(1)得

D(f)=(H(f))-1R(f)

(5)

对机振动试验控制，设R(f)，D(f)，C(f)的功率谱密度矩阵形式为GRR，GDD，GCC。为实现控制要求，须使

GCC=GRR

(6)

则式(3)变为

GDD=ZGRRZH

(7)

式中：Z为系统阻抗，且Z=H-1。GRR可用n个独立白噪声向量W和1个L表示，则可得驱动信号功率谱矩阵

GDD=ZLWWHLHZH

(8)

多轴随机振动试验改进型控制策略如图2所示[8]。在试验过程中，当参考谱与响应谱存在误差时，对L用比例均方根修正以实现控制目标，有

L(n+1)=L(n)·Δ(n)

(9)

因估计系统频响矩阵存在误差，其解耦补偿矩阵Z与真实频响H间的关系可描述为

HZ=I+E

(10)

式中：E为误差矩阵；I为单位阵。因此，需对其中的驱动信号进行迭代修正。设n为迭代次数，可得第n+1次迭代系统的实际响应谱矩阵

[GCC](n+1)=(HZ[L](n+1))(HZ[L](n+1))*

(11)

将式(9)代入式(11)，可得

[GCC](n+1)=(HZL(n)·Δ(n))(HZL(n)·Δ(n))*

(12)

经迭代修正后，所得的响应谱矩阵与参考谱矩阵的误差能达到规定精度要求，有

[GCC](n+1)≈GRR

(13)

本文用的比例均方根修正方法不会使功率谱对角线上元素出现零或负值，保证了控制系统的稳定性，能克服传统控制算法中的缺点。但比例均方根修正算法主要是针对功率谱矩阵的对角线上元素进行修正，而非对角线上的互谱控制并不单独考虑，互谱控制是通过修正自谱的过程自行完成，这对有严格互谱控制要求的振动试验不利。如能实时更新系统的频响特性，通过更新系统频响特性修正驱动信号，不仅可完成对功率谱矩阵的对角线上元素的自谱修正，而且能对非对角线上的互谱进行修正，则将从根本上实现对控制系统的功率谱修正[9]。

通过更新系统频响特性实现对驱动信号的修正是有条件的，取决于振动试验条件参考谱的设置。若设置的参考谱中各控制谱间的相干系数过高，接近于1时，则可知驱动谱矩阵必接近奇异，此时用此驱动信号作为更新系统频响特性的输入信号，作为分母的驱动谱矩阵将是奇异的，无法获得系统频响特性[10]。因此在系统控制中，根据设置参考谱中各控制谱的相干系数的取值选择系统修正的方法，当目标谱中相干系数小于0.95时，用更新系统频响矩阵的方法实现对驱动谱的修正；当目标谱中相干系数大于0.95时，用修正参考谱下三角矩阵的方式实现对驱动信号的修正，以此不断减小控制偏差。

3 优化算法仿真与实验验证

3.1多点随机控制算法仿真

为验证多点随机振动试验控制策略的有效性，用MATLAB软件对两激励两点控制进行仿真。系统的真实频响矩阵中各元素用二阶加速度模型代替，仿真试验中测试频响由在真实频响矩阵中加入2%的噪声信号获得，频率控制为20～2 000 Hz，谱线800条，报警限±1.5 dB。参考谱中两个自谱采用相同的谱型，均由上坡谱、平直谱和下坡谱组成，参数见表1。控制点1、2间的互谱设置为：相干函数0.1；相位差45°。

表1 参考谱的自谱设置

控制点1、2的自谱控制结果分别如图3所示。由图3可知：采用优化的多点随机控制策略各控制点的自谱控制效果较好，虽然在共振点附近的波动稍大，但仍能控制在±1.5 dB范围内，完全满足工程要求。

两控制点的互谱控制结果如图4所示。由图4可知：控制点1、2间的互谱控制效果较好，两控制点间的互谱控制在共振峰处相干函数波动稍大，但仍在工程允许的范围内，其他频率点控制效果很好，能满足控制要求。

3.2多点随机振动台实验验证

建立多点随机振动台实验系统，用两振动台对类似导弹的细长条试件进行振动试验，以验证本文多点激励随机振动控制策略的正确性。实验中设置的频率范围为20～2 000 Hz，幅值谱由上坡谱、下坡谱和恒定加速谱组成，两个目标谱的自功率相同，自闭环功率谱控制动态范围检定的参考自谱见表2。实验中两控制点间的互谱相位置为0°，相干函数为1。

随机试验自谱和互谱控制结果分别如图5、6所示。由图5、6可知：实际试验系统的自谱控制精度很高，响应自功率谱均在±1.5 dB范围内，完全满足工程试验要求；在20～2 000 Hz频率范围的奇异点上，相干函数和相位波动稍大，但都控制在试验规定的范围内，满足工程试验要求，由此证明本文的控制策略正确有效。

控制动态范围是衡量振动试验系统性能的重要指标，表示了控制系统同时控制最大响应信号和最小响应信号的能力，也反映了系统控制算法的优劣。

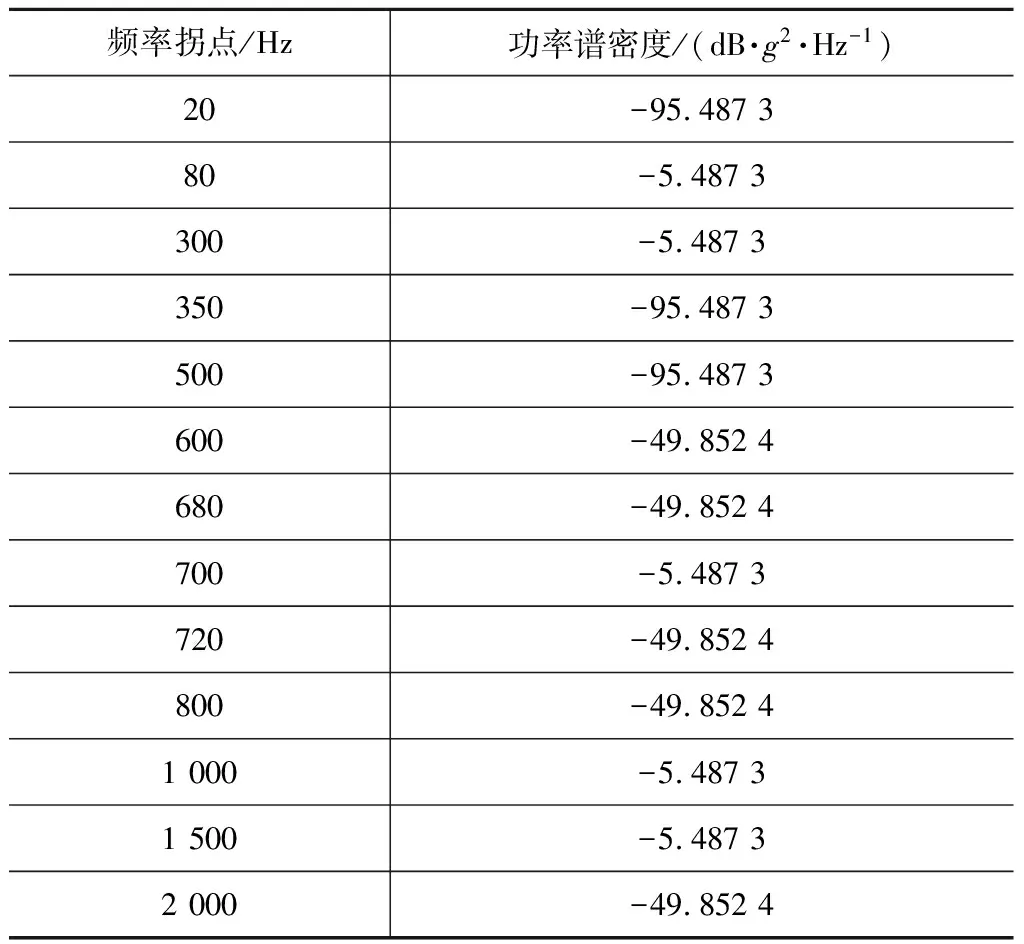
表2 自闭环功率谱控制动态范围检定的参考自谱

对多点随机振动试验控制系统进行自闭环控制实验，振动结果分别如图7、8所示。由图8可知：多点随机振动控制系统在频率20～2 000 Hz范围内各频率点的功率谱均获得很好的控制精度，在工程试验要求±3 dB范围内；在谱线为1 600条时，多点激励随机振动控制系统的控制动态范围为90 dB。

4 结束语

多轴多激励振动控制是一项理论性和工程性都很强的课题。振动系统内部组成较复杂，外部干扰强，影响控制精度的因素多，此外随机振动控制的实时性要求高也增加了控制难度[11]。本文通过理论和实验分析，首次提出用比例均方根迭代修正与系统频响特性更新综合均衡调控的方法提高试验控制系统驱动谱的跟踪精度，并给出了相应的控制策略与优化算法，较好地解决了由系统复杂性与耦合性产生的互谱控制不理想的难题，即不仅可完成对功率谱矩阵对角线上元素的自谱修正，而且能对非对角线上的互谱进行修正，从根本上实现了对控制系统的功率谱修正。用于验证算法的环节细长杆件两点随机振动控制实验结果表明：其控制响应自功率谱和动态范围均满足工程试验要求，且具备更高的控制稳定性和收敛速度。本文的优化控制策略可为基于复合型控制模式的多点随机振动控制领域提供一种算法优化的思路借鉴。随着对控制精度、控制速度和稳定性要求的不断提高，目前仍有诸多因素未能考虑，后续有待进一步研究。如多点随机振动试验控制策略研究，目前对互谱部分的控制主要是通过修正自谱以改善互谱控制效果，没有针对性地围绕互谱控制选择控制策略；多轴多激励系统多用于大型、重型设备的环境振动试验，其尺寸跨度大，远离振动台面的一端振动幅度大，当幅度超出一定范围后，其传递特性为非线性，此时单纯采用基于线性系统假设的控制方法就会失效，严重的会使系统失控，因此对大体积测试件特别是长杆件进行多点激励测试时，现有控制算法就不能完全满足要求，有必要进一步研究针对系统非线性特性的控制算法；在多轴多激励系统随机振动控制中，驱动信号随机化是影响谱估计精度特别是互谱估计精度的一个重要因素，因为随机化中的窗函数会影响信号的统计特性，从而影响频谱的变化，此外现有的驱动信号矩阵随机化方法计算量大，周期长，限制了多轴多激励振动的测试频宽，这也有待于专题研究[12-15]。

[1] STROUD R C, HAMMA G A, UNDERWOOD M A. A review of multiaxis/multiexciter vibration technology[J]. Sound and Vibration, 1996, 30(4): 20-27.

[2] 蒋瑜, 陈循, 陶俊勇. 基于时域随机化的超高斯真随机驱动信号生成技术研究[J]. 振动工程学报, 2005, 18(4): 491-494.

[3] 贺旭东. 多输入多输出振动试验控制系统的理论、算法及实现[D]. 南京: 南京航空航天大学, 2006.

[4] 陈章位, 于慧君. 振动控制技术现状与进展[J]. 振动与冲击, 2009, 28(3): 73-77.

[5] 叶凌云. 多轴向多激励随机振动高精度控制研究[D]. 杭州: 浙江大学, 2006.

[6] 王述成. 振动试验实时控制系统的研究[D]. 杭州: 浙江大学, 2006.

[7] UNDERWOOD M A, KELLER T. Recent system developments for multi-actuator vibration control[J]. Sound and Vibration, 2001, 35(10): 16-23.

[8] 陈家焱. 多点激励振动试验系统的控制策略研究[D]. 杭州: 浙江大学, 2011.

[9] 叶建华, 李传日. 多点随机振动试验控制技术[J]. 系统工程与电子技术, 2008, 30(1): 124-127.

[10] STEINWOLF A. Shaker random testing with low kurtosis: review of the methods and application for sigma limiting[J]. Shock and Vibration, 2010, 17(3): 219-231.

[11] 沈国重, 路甬祥. 多分辨随机振动控制算法[J]. 机械工程学报, 2001, 37(10): 14-18.

[12] 徐鉴. 振动控制研究进展综述[J]. 力学季刊， 2015, 36(14): 547-565.

[13] 邱汉平， 冯咬齐， 樊世超. 多轴随机振动试验控制技术研究[J]. 航天器环境工程， 2015, 32(5): 527-531.

[14] 叶焰杰， 陈怀海， 贺旭东, 等. 基于MATLAB/Simulink多输入多输出随机振动试验模拟研究[J]. 国外电子测量技术， 2016， 35(1)： 39-43.

[15] 孟光， 周徐斌， 苗军. 航天器重大工程中的力学问题[J]. 力学进展， 2016, 46(1): 268-322.

ResearchonDriverSpectraCouplingCorrectionBasedAlgorithmforMEMARandomVibrationTest

ZHONG Ke-ke1， CHEN Zhang-wei2， ZHANG Xiao-long1， CAO Xue-feng1

(1. Shanghai Spaceflight Precision Machinery Institute, Shanghai 201600, China;2. State Key Laboratory of Fluid Power and Control, Zhejiang University, Hangzhou 310027, Zhejiang, China)

To solve the problem of poor tracking precision and control stability in multi exciter/multi axis random vibration test mainly for aerospace products, the algorithm of coupling correcting optimization based on driving spectrum was studied in this paper. According to the vibration control principle and method of multi axis random test, proportional root-mean-square iteration correction and frequency character updating were applied to improve tracking precision of the driving spectrum for the test control system. The control strategy was put forward. The correcting method is selected according to the coherent coefficients of each control spectrum in the reference spectrum. The frequency character updating is used to implement the correcting of driving spectrum when the coherent coefficient is smaller than 0.95. The lower triangular matrix is used to implement the correcting of the driving signal when the coherent coefficient is larger than 0.95. The control deviation will be decreasing by this way. The simulation results of two-point and two exciters test showed that control of the auto-spectrum for the two control points was good which met the engineering requirement. The test results of the slender body on the two vibration tables showed that the control response of the auto-spectrum and dynamic scope met the requirement of the engineering test.

multi exciter/multi axis; random vibration; balanced regulation; tracking precision; control stability; driving spectrum; coupling correction; coherent coefficient

1006-1630(2017)05-0088-06

2016-12-28；

2017-02-28

国防基础科研基金项目资助

钟珂珂(1987—)，男，工程师，主要从事航天结构件环境试验与振动控制技术研究。

TB534.2

A

10.19328/j.cnki.1006-1630.2017.05.014