课堂教学讲究“挖” 注意背后的隐患—关于课堂教学设计的评价研究
2017-11-03江苏省常州市第一中学213003蒋建兵
江苏省常州市第一中学(213003) 蒋建兵
课堂教学讲究“挖” 注意背后的隐患—关于课堂教学设计的评价研究
江苏省常州市第一中学(213003) 蒋建兵
一.什么是背后的隐患
隐患就是在某个条件、事物以及事件中所存在的不稳定并且影响到个人或者他人安全利益的因素,它是一种潜藏着的因素,”隐”字体现了潜藏、隐蔽,而”患”字则体现了祸患,不好的状况.
在数学的教学当中,我们经常发现有一些问题,学生的答案是正确的,但解题过程却是错误的,如果条件稍加改变,就会导致错误,这就是本文所讲的背后隐患.为了解决该问题,我们在教学过程中就要讲究“挖”,挖出错误根源,挖出正确的解题思想和解题思路,从而很好的解决背后的隐患.
二.背后的隐患有哪些
1.条件的缺失引起的隐患
题1△ABC中角A、B、C的对边分别为a,b,c设向量且则sinA+sinB的取值范围是____.
错解因为


由正弦定理,得
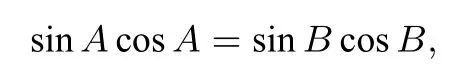
即 sin2A=sin2B. 又所以



所以

因此sinA+sinB的取值范围是
正解因为

由正弦定理,得
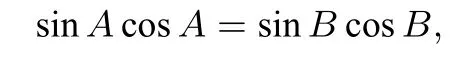
即 sin2A=sin2B. 又所以
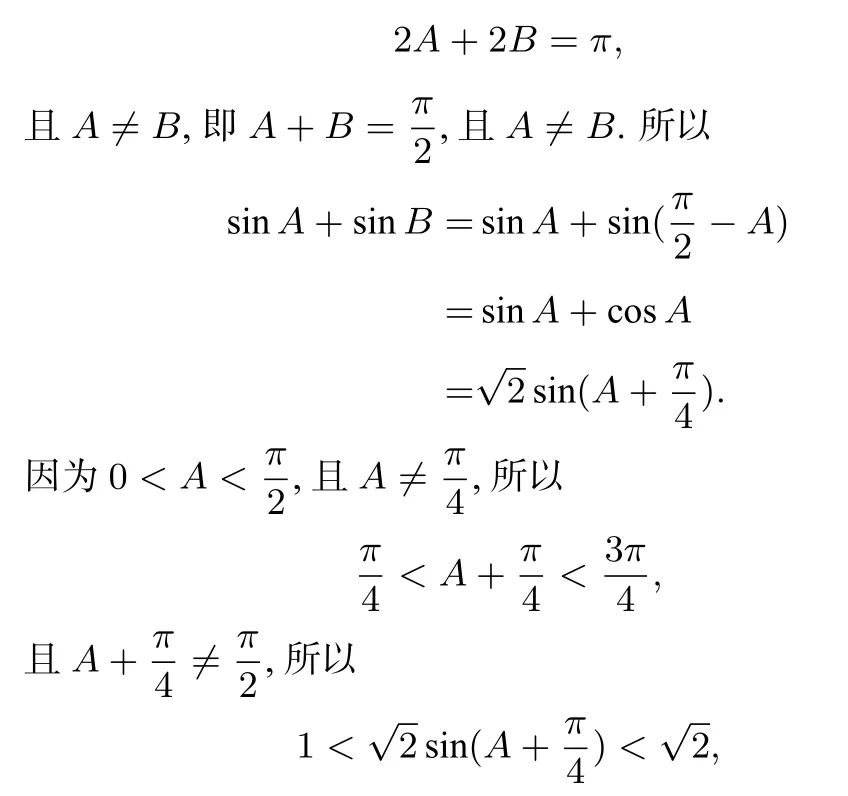
因此sinA+sinB的取值范围是
点评本题错解的解答过程,咋一看,非常严谨,每一步都很到位,答案看似正确.但细心的学生发现,答题者在三角函数的取值范围上犯了粗心的错误,关注到这一点,答案也就变成(1,然而回归到题目本身,要求A̸=B,所以从而最终正确答案又回到
2.解法的错用引起的隐患
题2 当x∈[−2,0]时,不等式x2−2ax−a≥0恒成立,则实数.a的取值范围是___.
错解∆=(−2a)2−4(−a)≤0.解得−1≤a≤0.
正解令

则f(x)min≥0,问题转化为二次函数区间最值问题.
①当a≤−2时,f(x)在[−2,0]上单调增,所以f(x)min=f(−2)≥0,所以不合题意,舍去;
②当−2<a≤0时,f(x)min=f(a)≥0,所以−a≤a≤0,因为−2≤a≤0,所以−1≤a≤0;
③当a>0时,f(x)在[−2,0]上单调减,f(x)min=f(0)≥0,所以a≤0,不合题意,舍去;
综上有:a∈[−1,0].
点评判别式法只专门针对二次函数,且定义域x∈R的情形,而本题定义域显然不符合要求,故解法选错.正确的解法应该选择函数最值法,这种解法就是专门针对定义域不满足x∈R的情形.若将题目改为:当x∈[−2,0]时,不等式x2−2ax+a≥0恒成立,则实数a的取值范围是___.如果仍然使用判别式法,则得到的结果为[0,1].
如果使用函数最值法,则得到结果为[0,+∞).此时就不像题2那样幸运了.所以在解题时我们要根据条件选择正确的、恰当的解法,消除隐患,将学习落到实处.
3.条件的不等价引起的隐患
题3已知函数(m为常数)为定义域上的奇函数,则m=___.
错解因为函数是奇函数,所以f(0)=0,可得m=1.
正解因为函数是奇函数,所以f(−x)=−f(x)恒成立,从而解得m=1.
点评根据奇函数的性质,使用f(0)=0去求解参数,必须建立在一个前提下,那就是f(0)要有意义,因为奇函数与f(0)=0并不等价.若f(0)没有意义或不清楚是否有意义,仍然使用f(0)=0去求解参数,就很容易造成漏解,如南通模考题就出过这样一道题:若函数(k为常数)在定义域上为奇函数,则k=____.如果只是单纯用f(0)=0去求解,只能得到k=1,而用f(−x)=−f(x)恒成立去求解,就能得到准确答案k=±1.
题4△ABC内接于圆O,若有,则∠C=____.
错解由
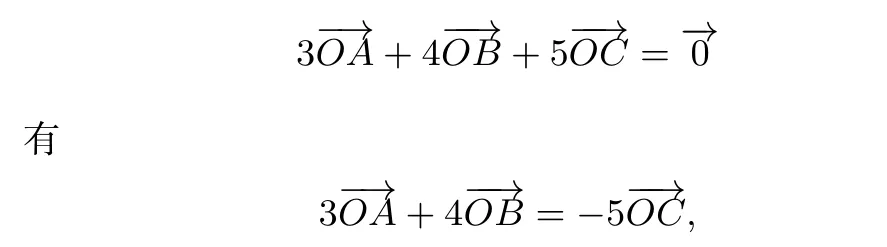
正解由

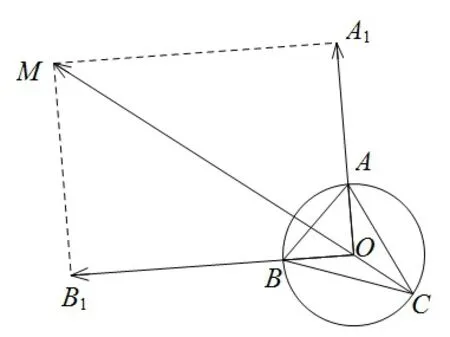
图1

图2
点评利用平方的手段得到从而得到∠AOB=90°,然后错解只是单纯根据“同弧所对的圆周角是圆心角的一半”这一结论,简单得到∠C=45°.若题目变化为:△ABC内接于圆O,若有则∠C=____.按照同样的方法,我们仍然会得到∠C=45°,题目的条件发生变化,这样的答案显然是错误的,主要原因是平方后的式子是完全一样的,平方不是等价转化,故在正确解法中,再运用了数形结合的思想,根据图形(图1)我们准确得到结果.而变题,我们则需要结合图2,得到∠C=135°.
正确的答案背后不一定就说明解答就完全正确,在条件没有挖掘全面的情况下完成解答,带来了一定的迷惑性,这就需要我们考虑全面题目的条件,包括外在的和内在的,只有这样,才能真正掌握,真正理解,真正做对,否则就产生了隐患.
三、教学在设计时应该怎么挖
1.挖课堂
课堂教学是学生学习的主阵地,课堂教学设计的成功与否直接决定了这堂课的教学效果,尤其是学生容易产生问题的地方.所以我们在设计时应该注意挖掘如下几个方面:
第一,深入细致的研究教材,充分挖掘教材中的有价值的素材,并根据需要适当的补充一些素材.例如在《函数零点》的教学过程中,书本中给出函数零点的存在性定理,而该定理只能用于判定有没有,不能解决存在几个零点的问题,所以我们收集资料,整理归纳,从而得出了更加完整的结论,完成了对教材的二次开发.
第二,了解学生的真正需求,挖掘学生的易错点,设计有针对性的教学方式.例如在《二次函数问题》的教学过程中,初高中的侧重点有所不同,高中生缺乏的是对含参问题的处理,所以在讲解根的分布与区间最值问题时,我们可多用讨论、研究、发现等方法,按教学思路逐步深入地呈现.
2.挖订正
杭州市余杭区良渚中学的经验告诉我们“订正作业是教学过程中的一个重要环节,它完成的好坏直接关系到学生对知识的掌握情况,而且对强化教学效果,进一步提高教学质量和促进教学改革具有重要意义”.
错题订正后仍旧出错,这是目前最普遍的现象.充分挖掘问题根源,寻找到更好的订正策略,对提高教学质量起至关重要的作用.所以在开展学生自我反思式的作业订正时,还应注意以下几点:
第一,让学生划出做错的地方.这样做的目的就是要让学生自己找到错误的问题所在,只有自己明白错在哪才有办法对问题进行整改.
第二,让学生找出做错的直接原因.要做到这一点比较难,我们教师在平时就要注意训练学生自己分析原因的本领.如:在课堂练习(学生上黑板时)时结合具体情况讲解、甚至还要组织讨论,使他们能正确分析导致做错的直接原因.当学生订正后交作业时,教师必须认真检查其分析是否正确,多次练习后才能达到要求.
第三,要求学生针对做错的直接原因,指出应如何弥补.这是订正工作中的一个难点,在实际操作中发现,学生的做法有时候常是“我要认真听课”“下次我要仔细计算”之类的回答.遇到这样的回答,最好说:“你看这就是重要的,上到这你更要仔细听,才能会做.”时间长了学生就开始会听课了,这样也就达到了作业是课堂的延伸和必要补充的作用.
3.挖复习
“刀不磨要生锈,人不学习要落后.”学习中,只有把学过的知识经常的复习,才能牢记在心中.复习在学习中起到了巩固、强化的作用,是将知识掌握的一个重要环节.遗忘规律告诉我们,人的初次记忆,只能在脑海中停留1 2天,再次记忆,也只能停留15天左右,只有一遍又一遍的经常性去看,去记,才能牢牢地把知识记在脑海中.
总之,数学的教学我们不能只看表象,要挖掘问题的根源,寻找相应的解决措施,扎扎实实的落实下去,才会看到最后的彩虹.
