矩阵特征值在矩阵中的作用

林大华，戴立辉

（闽江学院 数学系，福建 福州 350108）

矩阵特征值在矩阵中的作用

林大华，戴立辉

（闽江学院 数学系，福建 福州 350108）

用矩阵的特征值对矩阵的行列式、可逆性、迹、秩、对角化、相似、正定性以及一些特殊矩阵进行了刻画.

矩阵；特征值；行列式；可逆性；迹；秩；对角化；相似；正定性

1 引言与预备知识

矩阵的特征值是线性代数理论的一个重要组成部分，具有广泛的应用.本文主要综述特征值在矩阵的行列式、可逆性、迹、秩、对角化、相似、正定性以及一些特殊矩阵等矩阵理论上的若干作用，从中可以看到，矩阵理论中的许多问题可以用矩阵的特征值加以刻画.

本文用Pn×n表示数域P上全体n阶方阵集合,用Pn表示数域P上全体n维向量集合,用P[x]表示数域P上全体一元多项式集合，用Tr(A)表示矩阵A的迹.未经说明的记号参看文献[4].

设A∈Pn×n,λ∈P,若存在非零 n维向量 α∈Pn,使得Aα=λα,则称 λ是A的特征值,α是 A的属于λ的特征向量.

对A∈Pn×n，矩阵λE-A称为A的特征矩阵，多项式fA(λ)=|λE-A|称为 A 的特征多项式.

λ∈P是矩阵A∈Pn×n的特征值充分必要条件是λ是特征多项式的根.

矩阵A∈Pn×n的特征多项式的根，称为A的特征根.注意,A的特征根未必是A的特征值.A的特征根λ是特征值充分必要条件是λ∈P.由于多项式在复数域上总是有根,所以矩阵的特征根总是存在的，但特征值未必总存在.因此,n阶方阵的特征值个数不超过n.A的特征值λ作为特征根的重数称为λ的代数重数.

若 λ∈P是矩阵 A∈Pn×n的特征值，则集合 Vλ={α∈Pn|Aα=λα}是 Pn的子空间，称为属于 λ的特征子空间.Vλ的维数称为λ的几何重数.

若 λ∈P 是矩阵 A∈Pn×n的特征值，f(x)∈P[x]，则 f(x)是 f(A)的特征值；当A可逆时，λ-1是A-1的特征值.

两个相似的同阶方阵有相同的特征根,因而有相同的特征值.

2 矩阵特征值的若干作用

2.1 方阵的行列式

若 n 阶方阵 A 的 n 个特征值为 λ1,λ2,…,λn，则有

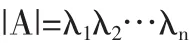
例1 设-2，3，-1是三阶方阵A的特征值，求|A3-6A+11E|.

解 令 f(x)=x3-6x+11,则 f(A)=A3-6A+11E.因为 A 的特征值为-2,3,-1,所以f(A)的特征值为f(-2)=15,f(3)=20,f(-1)=16,故

|f(A)=A3-6A+11E|=|f(A)|=f(-2)f(3)(-1)=15×20×16=4800

2.2 方阵的可逆性

n阶方阵A是可逆矩阵的充分必要条件是A的特征值均非零.

例2 设n方阵A的特征值全是实数.证明,若E-A的特征值的绝对值都小于1,则A可逆.

证明 设A的全部特征值为λ1,λ2,…,λn则E-A的全部特征值为

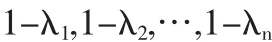
由 1-λi全是实数,且 |1-λi|＜1,可得 -1＜1-λi＜1,即 0＜λi＜2(i=1,…n).于是A的特征值均非零,故A可逆.

2.3 方阵的迹

若 n 阶方阵 A 的 n 个特征值为 λ1,λ2,…,λn，则有

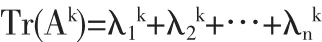
事实上,由 λ1,λ2,…,λn是 A 的 n 个特征值，可知 λ1k,λ2k,…,λnk是 Ak的 n 个特征值.于是有

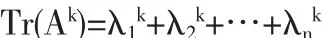
推论 若 A=(aij)n×n,则有

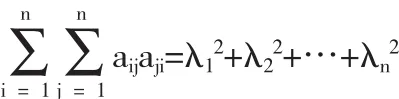
2.4 方阵的相似

若n阶方阵A的特征根均为特征值,则

(1)相似于上(下)三角形矩阵

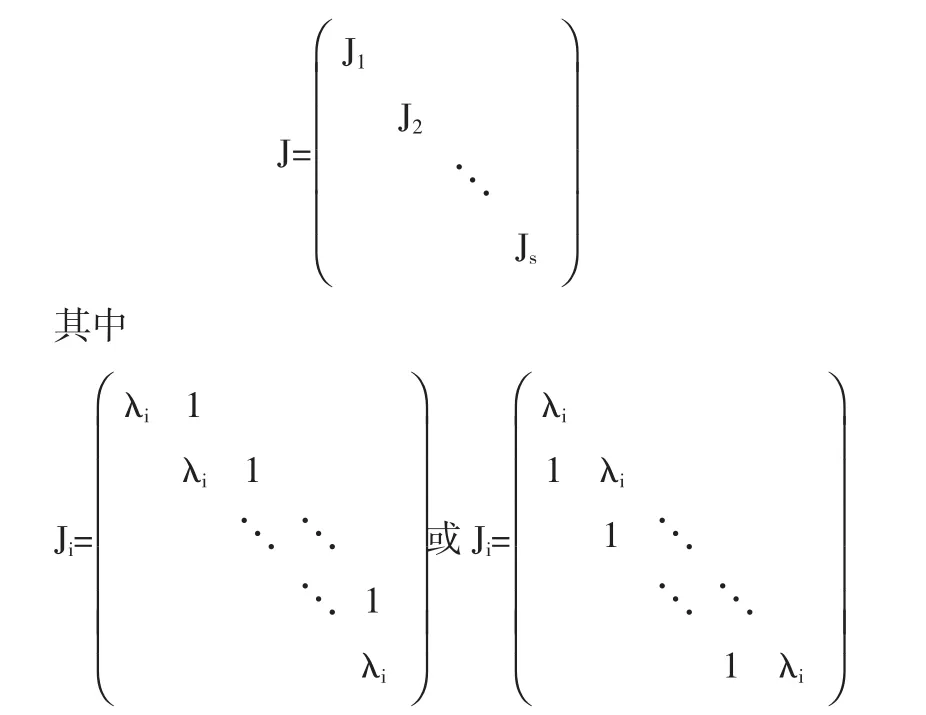
λi(i=1,2,…,s)是A的全部特征值.Ji的阶数是λi的代数重数.

J称为A的若当标准形.

(2)若n方阵A,B有相同的特征根,且每个特征根的重数也一样,则A,B相似.

(3)若n方阵A,B的特征根不完全相同,则A,B不相似.

2.5 方阵的秩

若n阶方阵A的特征根均为特征向量,则

(1)当0是A的k重特征值时,有秩(Ak+l)=n-k(l≥0).

(2)当0是A的k重特征值时,秩(A)=n-k的充要条件是秩(A)=秩(A2).

事实上,(1)把A的若当标准形中特征值不是0的子块放在一起记为B,把特征值为0的子块放在一起记为B0,则有

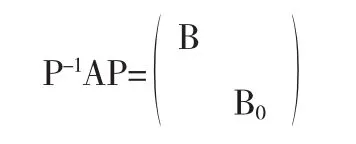
其中B可逆.

由于0是A的k重特征值,故B0是k阶方阵.从而B0中的每个子块Ji的阶数≤k,于是由

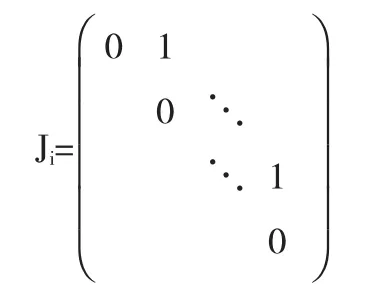
可知 Jik=0,故 B0k=O,因此

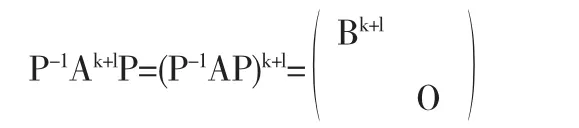
但B是n-k阶可逆方阵,故秩(Ak+l)=n-k.

(2)由(1)的证明可知,有

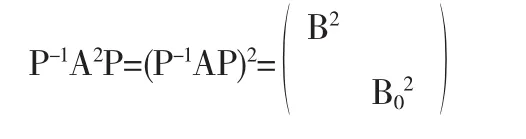
于是有

秩(A)=秩(B)+秩(B0) 秩(A2)=秩(B2)+秩(B02)

因为B是n-k阶可逆方阵,所以秩(B)=秩(B2) 从而秩(A)=秩(A2)的充要条件是秩(B0)=秩(B02).

若B0中的子块Ji的阶数大于1,则必有秩(Ji)＜秩(Ji2).故秩(B0)=秩(B02)的充要条件是Ji的阶数为1,即Ji=O,故秩(B0)=秩(B02)的充要条件是B0=O,即秩(A)=n-k.

2.6 方阵的对角化

n阶方阵A可对角化充分必要条件是A的特征根均为特征值,且每个特征值的代数重数等于几何重数.此时,对角矩阵若不考虑对角线上的元素排列次序是唯一的,并且对角线上的元素均为A的特征值.

推论1 若n阶方阵A有n个不同的特征值λ1,λ2,…,λn,则A可对角化且对角矩阵对角线上的元素是A的特征值.即存在可逆矩阵Q,使得

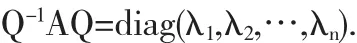
推论2 若n阶方阵A可对角化,则A是零矩阵充分必要条件是A的特征值全为零.

2.7 实对称矩阵

实对称矩阵的特征值均为实数.若 λ1,λ2,…,λn是 n 阶实对称矩阵A的n个特征值,则A正交相似于对角矩阵diag(λ1,λ2,…,λn),即有正交矩阵 Q,使得推论实对称矩阵A是正定矩阵充分必要条件是A的特征值均大于零.

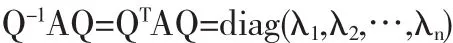
2.8 一些特殊矩阵

若方阵A的特征根均为特征值，则

(1)A是幂零矩阵充分必要条件是A的特征值均为零.

(2)若A的特征值不全是单位根,则A不可能是幂幺矩阵.

(3)若A的特征值不是1或0,则A不可能是幂等矩阵.

(4)若A的特征值不是1或-1,则A不可能是对合矩阵.

〔1〕杨子胥.高等代数习题解(修订版)[M].济南:山东科学技术出版社，2009.11.

〔2〕杨子胥.高等代数精选题[M].北京:高等教育出版社，2010.1.

〔3〕钱吉林.高等代数题解精辟[M].北京:中央民族大学出版社,2005.12.

〔4〕北京大学数学系前代数小组．高等代数（第四版）[M]．北京：高等教育出版社，2014.2.

O152

A

1673-260X（2017）10-0008-02

2017-07-03