矩阵的两个幂等矩阵组合的可逆性

曹元元， 左可正， 熊 瑶

(湖北师范大学 数学与统计学院， 湖北 黄石 435002)

矩阵的两个幂等矩阵组合的可逆性

曹元元， 左可正*， 熊 瑶

(湖北师范大学 数学与统计学院， 湖北 黄石 435002)

利用幂等矩阵的性质及两个幂等矩阵的和与差的可逆性，研究了两个幂等矩阵P，Q在条件(PQ)2=PQ下，它们的组合T=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(QP)2，(a，b，c，d，e，f，g∈，ab≠0)的可逆性，并给出它的求逆公式．

幂等矩阵; 可逆性; 组合

幂等矩阵及幂等算子在线性代数与算子代数中是很重要的研究对象.1990年，武培元在文献[1]中证明了每个复数域上的无限维希尔伯特空间上的有界线性算子是不超过五个幂等算子的线性组合.2004年，Rabanovic在文献[2]中证明了特征为零的域上任意一个矩阵都可以表示成三个幂等矩阵的线性组合，可见幂等矩阵及幂等算子对于其它矩阵及其他算子的研究起着重要的作用．

近年来，国内外很多学者对各种特殊矩阵的组合及组合的相关性质进行了广泛和深入的研究，并得到了一些很好的结果，而这些结果都是将其应用到实际的重要前提.如在文献[3]和文献[4]中，Gro和Trenkler，Koliha等研究了两个幂等矩阵的和与差的可逆性问题.在文献[5]中，Baksalary和Baksalary给出了两个幂等矩阵的线性组合仍是幂等矩阵的完全分类.在文献[6]中，Baksalary和Baksalary给出了两个幂等矩阵线性组合的可逆性与组合系数的关系.在文献[7]中，杜鸿科、姚喜研和邓春源讨论了希尔伯特空间上两个幂等算子组合的可逆性与组合系数的关系.在文献[8]和文献[9]中，Koliha和Rakocevic、左可正研究了两个幂等矩阵的线性组合aP+bQ及两个幂等矩阵的组合aP+bQ-cPQ(其中P，Q是两个n阶幂等矩阵，a，b，c均为复数，且ab≠0)的可逆性问题.在文献[10]中，左可正得出了几个幂等元之差可逆的充要条件.在文献[11]中，左可正和谢涛研究了两个幂等算子组合aP+bQ-cPQ-dQP-ePQP(其中P，Q是两个n阶幂等矩阵，a，b，c，d，e均为复数，且ab≠0)的可逆的充要条件.在文献[12]和[13]中，Koliha和Rakocevic研究了不同幂等矩阵组合的可逆性．

本文将进一步研究两个幂等矩阵P，Q在条件(PQ)2=PQ下，它们的组合T=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(QP)2，(a，b，c，d，e，f，g∈，ab≠0)的可逆性，并给出它的求逆公式．

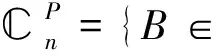
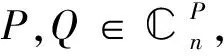
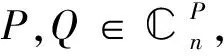
(a，b，c∈，ab≠0)且:

1)当a+b+c=0时，aP+bQ+cPQ可逆当且仅当P-Q可逆;

2)当a+b+c≠0时，aP+bQ+cPQ可逆当且仅当P+Q可逆．

1 T=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(QP)2的可逆性

本节给出T=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(QP)2(a，b，c，d，e，f，g∈，ab≠0)的可逆性的充要条件，我们要分a+b+c+d+e+f+g=0与a+b+c+d+e+f+g≠0两种情况来讨论．

证明必要性.当T可逆时，对∀α∈N(P-Q)有Pα=Qα，从而

Tα=(aP+bQ+cPQ+dQP+ePQP+

fQPQ+g(QP)2)α=

(a+b+c+d+e+f+g)Pα=0，

由T可逆得出α=0，从而可得P-Q可逆．

充分性.当P-Q可逆时，对∀α∈N(T)有Tα=0，即

Tα=(aP+bQ+cPQ+dQP+ePQP+

fQPQ+g(QP)2)α=0，

(1)

将(1)左乘P，并注意到(PQ)2=PQ可得

(aP+bPQ+cPQ+fPQ+dPQP+

ePQP+gPQP)α=0.

(2)

将(1)左乘PQ，可得

(aPQP+bPQ+cPQ+dPQP+ePQP+

fPQ+gPQP)α=0.

(3)

组合(2)式和(3)式，并注意a≠0，得

Pα=PQPα.

(4)

将(1)左乘Q，并利用(4)式计算可得

(aQP+bQ+cQPQ+dQP+eQP+

fQPQ+gQP)α=0.

(5)

将(2)左乘QP，并利用(4)式计算可得

(aQP+bQPQ+cQPQ+dQP+eQP+

fQPQ+gQP)α=0.

(6)

组合(5)式和(6)式，可得出

Qα=QPQα.

(7)

由(4)式和(7)式可得出

(P-Q)3α=(P-PQP-Q+QPQ)α=0，

这样由P-Q可逆知α=0，从而得出T可逆.

证明充分性.当P+Q可逆时，对∀α∈N(T)有Tα=0，类似于定理1中充分性证明的推导可得出

Pα=PQPα，Qα=QPQα.

(8)

那么

(P+Q)3α=(P+2PQ+PQP+Q+2QP+

QPQ)α=2(P+Q)2α.

(9)

这样由P+Q可逆及(8)式可得出

(P+Q)α=2α.

(10)

将 (10)式分别左乘P和Q可得出

Pα=PQα，Qα=QPα.

(11)

由Tα=0及(8)、(11)式可得

Tα=(a+c+e)Pα+(b+d+f+g)Qα=0.

(12)

将(12)式分别左乘P和Q可得

(a+b+c+d+e+f+g)Pα=0，

(a+b+c+d+e+f+g)Qα=0，

这样由a+b+c+d+e+f+g≠0可得Pα=Qα=0，(P+Q)α=0，而P+Q可逆，所以α=0，从而得T可逆．

必要性.当T可逆时，对a，b，c，d，e，f，g作如下分类来证明P+Q可逆：

情形1当b+c+f=0时，对∀α∈N(P+Q-PQ)，有(P+Q-PQ)α=0，左乘P得出Pα=0，PQα=Qα，此时Tα=(b+c+f)Qα=0.所以由T可逆知α=0，从而P+Q-PQ可逆，由引理2得出P+Q可逆．

情形2当a+d+e+g=0时，对∀α∈N(P+Q-QP)，则(P+Q-QP)α=0，左乘Q得出Qα=0，QPα=Pα，此时Tα=(a+d+e+g)Pα=0.因为T可逆，所以α=0，从而知P+Q-QP可逆，由引理2得出P+Q可逆．

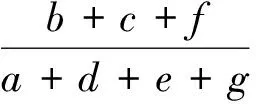
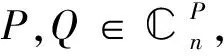
①a+b+c+d+f≠0时，T可逆当且仅当P+Q可逆;

②a+b+c+d+f=0时，T可逆当且仅当P-Q可逆．

①a+b+c+d+f≠0时，T可逆当且仅当P+Q可逆;

②a+b+c+d+f=0时，T可逆当且仅当P-Q可逆．

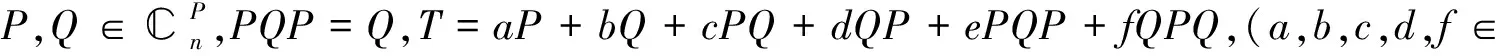
①a+b+c+d+f≠0时，T可逆当且仅当P+Q可逆;

②a+b+c+d+f=0时，T可逆当且仅当P-Q可逆.

其中，定理1和定理2推广了Koliha和Rakocevic在文献[8]以及左可正在文献[9]、[11]和[14]中的结论．

2 T=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(QP)2的逆的表达式

本节给出在P-Q可逆与P+Q可逆的条件下T的逆的表达式．

证明因为P-Q可逆，所以由引理1知P+Q可逆，这样由定理1和定理2知，T总是可逆的.因为P-Q可逆，所以由引理1知I-PQ也是可逆的，从而由(PQ)2=PQ得出PQ=0，此时T=aP+bQ+dQP，下面来计算T-1．

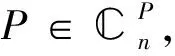
P=U(Ir⊕0)U-1，

(13)

其中r=r(P).令

(14)

其中Q1∈r×r，Q2∈r×(n-r)，Q3∈(n-r)×r，Q4∈(n-r)×(n-r)．

由PQ=0，通过(13)式和(14)式计算可得出Q1=0，Q2=0．

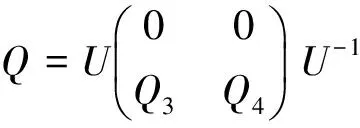
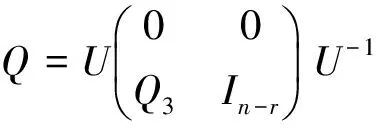
(15)

由(3.1)式和(3.3)式计算可得出

P+Q-QP=I.

(16)

由(13)、(15)结合(16)式，并注意到PQ=0，所以有

(17)

通过(17)式可计算出

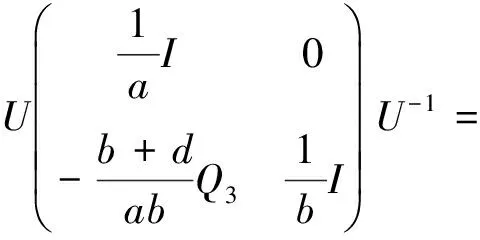
证明因为T可逆，所以由定理2知P+Q可逆，通过简单的计算可得出下式:

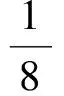
(18)

因为P+Q可逆，这样由(18)式得出

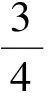
(19)

对(19)式分别左乘P和右乘Q可得出

PQ=PQP，PQ=QPQ，

(20)

从而

(QP)2=PQP=PQ，

(21)

组合(19)式和(21)式可得

P+Q-QP=I，

(22)

下面通过矩阵分块来计算T-1．

由(22)式结合(13)、(14)式可得出

Q2=0，Q4=In-r，

(23)

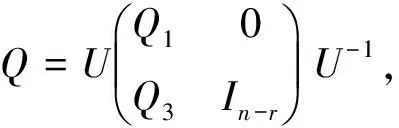
(24)

由(24)式对Q1，Q3作进一步的分块可得

Q1=L(Ir1⊕0)L-1，Q3L=(0，Y)，

(25)

其中Y∈(n-r)×(n-r)，L是一个r级可逆阵．

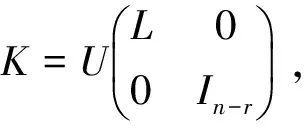
(26)

组合(20)式、(21)式和(26)式可得出

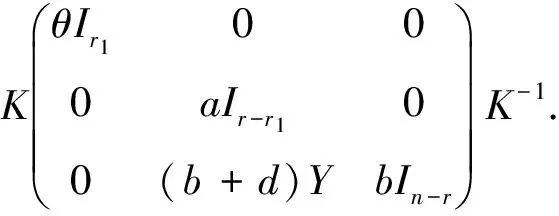
(27)

通过(27)式可计算出

3 实例计算

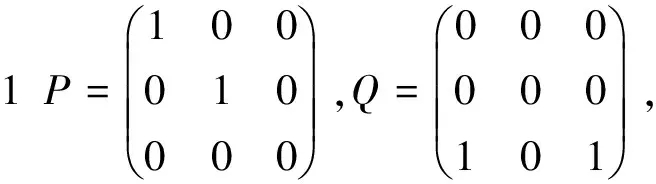
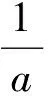
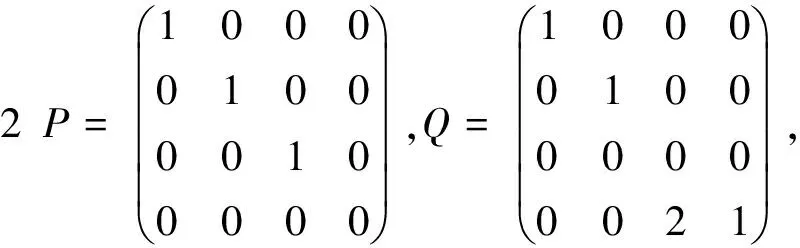
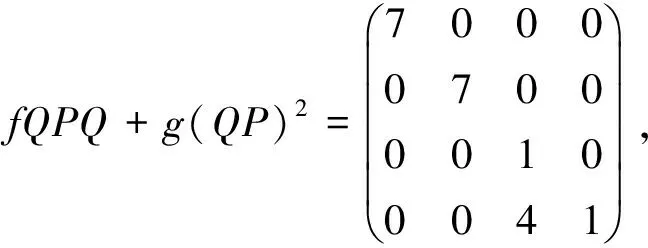
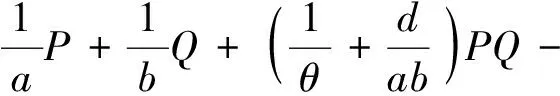
[1] WU P Y. Sums of idempotent matrices[J]. Linear Algebra Appl， 1990，142(142): 43-54．

[2] RAbANOVIC V. Every matrix is linear combination of three idempotents[J].Linear Algebra Appl， 2004，390(4):137-143．

[4] KOLIHA J J， RAKOCEVIC V， STRASKRABA I. The difference and sum of projectors[J].Linear Algebra Appl， 2004，388(5):279-288．

[5] BAKSALARY J K， BAKSALARY O M. Idempotency of combinations of three idempotent matrices，two of which are disjoint[J]. Linear Algebra and its Appl. 2004，388(1):67-78．

[6] BAKSALARY J K， BAKSALARY O M. Nonsingularity of linear combinations of idempotent matrices [J]. Linear Algebra Appl， 2004，388(1):25-29．

[7] DU H，YAO X，DENG C. Invertibility of linear combination of two idempotents[J].Pro Amer Soc， 2006，134(5):1451-1457．

[8] KOLIHA J J， RAKOCEVIC V. The nullity and rank of linear combinations of idempotent matries[J].Linear Algebra Appl， 2006，418(1):11-14．

[9] ZUO K. Nonsingularity of the difference and the sum of two idempotent matrices[J].Linear Algebra Appl， 2010，433(2):476-482．

[10] 左可正. 关于幂等元之差的可逆性[J].数学杂志， 2007，27(1):96-101．

[11] ZUO K， XIE T. Nonsingularityof combinations of idempotent matrices [J].Journal of Mathematics， 2009，29(3):285-288．

[12] KOLIHA J J， RAKOCEVIC V. Invertibilityof the sum of idempotents[J]. Linear Multilinear Algebra， 2002，50(4):285-292．

[13] KOLIHA J J， RAKOCEVIC V. Invertibility of the difference ofidempo-tents[J].Linear and Multilinear Algebra， 2003，51(1):97-110．

[14] ZUO K. The nullity and rank of combinations of idempotent matries[J].Journal of Math， 2008，28(6):619-622．

[15] LIU X J， WU L L，BEN＇ITEZ J L . On the group inverse of linear combinations of two group invertible matrices[J]. Electronic Journal of Linear Algebra. 2011，22(1):490-503．

Invertibilityofthecombinationoftwoidempotentmatriceswhichproductsisidempotentmatrix

CAO Yuanyuan， ZUO Kezheng， XIONG Yao

(Department of Mathematics， Hubei Normal University， Huangshi， Hubei 435002)

By using the nonsingularity of difference and sum of two idempotent matricesP、Q，we study the invertibility of the combinationT=aP+bQ+cPQ+dQP+ePQP+fQPQ+g(PQ)2，(a，b，c，d，e，f，g∈，ab≠0)under the condition of(PQ)2=PQ. Furthermore， the expression of its inverse is provided in this paper．

idempotent matrix; invertibility; combination

O151.2

A

2017-02-27.

国家自然科学基金项目(11271105); 湖北省教育厅重点项目(D20122202)．

*通讯联系人. E-mail: xiangzuo28@163.com.

10.19603/j.cnki.1000-1190.2017.05.001

1000-1190(2017)05-0569-05