“直观想象”在全国卷函数试题中的应用探析*

林丽娟 林新建

福建省漳州第一中学 (363000)

“直观想象”在全国卷函数试题中的应用探析*

林丽娟 林新建

福建省漳州第一中学 (363000)

“直观想象”是高中数学核心素养的重要内涵.

“直观想象”是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程.

“直观想象”主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系；构建数学问题的直观模型，探索解决问题的思路.

下面以全国卷函数试题为例，就“直观想象”在解题中的应用作一探析，以飨读者.

1.运用“直观想象”引领图形特征的感知

运用“直观想象”策略，可以较好地引领函数图形特征的感知，进而借助图形特征可将问题轻松予以解决.

例1 (2009年高考新课标卷Ⅰ理科第9题)

已知直线y=x+1与曲线y=ln(x+a)相切，则a的值为( ).

A．1B．2C． -1D．-2

解析：本题若依常规方法求解有一定的运算量，但若运用“直观想象”策略予以求解根本不用计算，瞬间可得答案.

由“直观想象”可知：函数y=ln(x+1)的图像在直线y=x+1的下方，从而知欲使得曲线y=ln(x+a)与直线y=x+1相切，则曲线y=ln(x+a)必是曲线y=ln(x+1)向左平移而得，结合选项容易排除A、C、D，故选B.

例2 (2013年高考新课标卷Ⅰ理科16题)

若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称，则f(x)的最大值是___________.

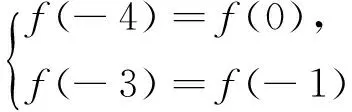
其实，若运用“直观想象”策略对函数的图形特征作感知，可将问题轻松予以解决，运算量也很小.

由“直观想象” 知函数f(x)有两个零点1，-1，又f(x)的图像关于直线x=-2对称，故f(x)另有两个零点-3，-5，所以f(x)=-(x-1)(x+1)(x+3)(x+5).

再运用“直观想象”对f(x)的图像作感知，可知若f(x)的图像向右平移两个单位，其最大值不会改变，于是我们可将求函数f(x)的最大值转化为求函数h(x)=-(x-3)(x-1)(x+1)(x+3)的最大值了.

至此，直接配方即得h(x)=-(x2-5)2+16，故f(x)的最大值为16.

与高考参考解答比较，这样的解法另辟蹊径，轻松快捷，凸显了“直观想象”在引领函数图形特征感知、简化解题途径上的重要作用.

2.运用“直观想象”引领形数关系的建立

运用“直观想象”策略，可以较好地引领形数关系的建立，进而借助形的直观可将函数问题轻松予以解决.

例3 (2012年高考新课标卷Ⅰ理科21题)

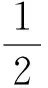
(Ⅰ)求f(x)的解析式及单调区间；

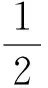
解析：本题难在第(Ⅱ)问，许多考生不知从何入手，望题兴叹而已.

其实，若能运用“直观想象”策略建立起形与数之间的关系，问题可轻松获得解决.

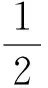
由“直观想象”知，要使上式对一切实数x∈R成立，函数y=ex的图像必须在函数y=(a+1)x+b图像的上方，故必须有a+1>0，因此，要使(a+1)b最大，必须b>0.

再由“直观想象”知，直线y=(a+1)x+b必须与函数y=ex的图像相切.至此问题就容易解决了.

设切点为P(x0,y0)，则y0=ex0=(a+1)x0+b，且ex0=a+1.联立可得x0=ln(a+1)，b=(a+1)-(a+1)ln(a+1).

故(a+1)b=(a+1)2-(a+1)2ln(a+1).

与高考参考答案比较，这样的解法另辟蹊径、简洁优美，使我们感到——运用“直观想象”策略可轻松引领形数关系的建立，这样不但回避了分类讨论带来的麻烦，而且思维更加流畅、更容易接近问题的本质.

3.运用“直观想象”引领解题思路的生成

运用“直观想象”策略，可以较好地引领解题思路的自然生成，使得难题的解决进行得轻松自在，轻而易举.

例4 (2010年高考新课标卷Ⅰ理科21题)

设函数f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的单调区间；

(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围.

解析：本题第(Ⅱ)问很难，运用常规方法如“参数分离”等均无法将其解决，怎么办？

其实，若运用“直观想象”策略对函数的图像作探究，不难探索出问题求解的简洁思路，将问题的解答臻于完美.

因为f(0)=0，即f(x)的图像过原点，而f(x)≥0对一切x≥0都成立，所以由“直观想象” 知，f(x)的图像在x=0右侧附近必须递增，所以f′(x)≥0对x=0右侧附近成立.

又因为f′(x)=ex-1-2ax，f′(0)=0，所以同样由“直观想象”知，f′(x)的图像在x=0右侧附近也必须递增，从而f″(x)≥0对x=0右侧附近成立.

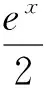
有了这个发现就好办了，接下来我们只要证明：

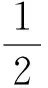
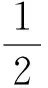
证明：由f(x)=ex-1-x-ax2知，f′(x)=ex-1-2ax，f″(x)=ex-2a.

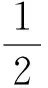
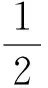
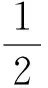
由于“直观想象”，我们猜想出a的范围，进而将问题转化而轻松求解，凸显了“直观想象”在探索问题解决思路、简化难题求解途径上的重要作用.

“直观想象” 在数学解题中有着重要的作用，在直观想象核心素养的形成过程中，学生能够进一步发展几何直观和空间想象能力，增强运用图形和空间想象思考问题的意识，提升数形结合的能力，感悟事物的本质，培养创新思维，平时教学和高考复习都应予以足够的重视.

*本文是2016年度漳州市基础教育课程教学研究课题“基于全国考试的高三有效性复习研究”的研究成果.