2016年全国高中数学联赛四川预赛15题的探究与推广

刘 刚 赵 毅

北京市第十二中学 (100071)

2016年全国高中数学联赛四川预赛15题的探究与推广

刘 刚 赵 毅

北京市第十二中学 (100071)

1试题

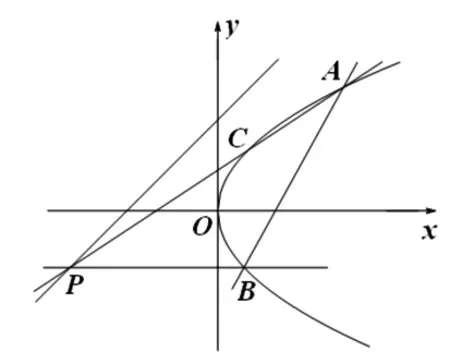
图1

(2016年全国高中数学联赛四川预赛)如图1，已知抛物线y2=2px过定点C(1,2)，在抛物线上任取不同于点C的一点A，直线AC与直线y=x+3交于点P，过点P作x轴的平行线交抛物线于点B．

(1)求证：直线AB过定点；

(2)求△ABC面积的最小值．

试题考查了抛物线的标准方程、几何性质、直线与抛物线的位置关系及定点、面积最值问题，考查了方程、转化与化归、分类与整合等数学思想以及坐标法的应用，检验了运算求解、分析问题与解决问题的能力．试题解法灵活，内涵丰富，是一道好题．

2解法探究

(1)问的探究

分析1:先设出A点坐标，求出直线AC的方程，与直线y=x+3的方程联立得到P点坐标，然后根据直线PB与x轴平行求出点B的坐标，最后建立直线AB的方程从而得到答案．

分析2:先设出直线AB的方程以及点A，B的坐标，然后根据直线PB与x轴平行表示出点P的坐标，利用A，P，C三点共线，由斜率建立等式关系，最后借助根系关系并消元得到一元一次方程，根据一元一次方程恒成立进行求解．

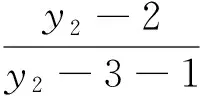
(2)问的探究

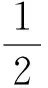
3推广

经过对本题的深入研究，可得以下定理及推论．

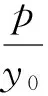
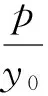
推论1 在抛物线y2=2px(p>0)上任取不同于顶点O的一点A，直线AO与直线x=a(a<0)交于点P，过点P作x轴的平行线交抛物线于点B，则直线AB过定点(-a,0)．

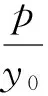
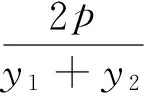
推论2 过定点Q(a,0)(a>0)的直线交抛物线y2=2px(p>0)于A，B两点，过点B作x轴的平行线交直线AO(O为抛物线的顶点)于点P，点Q关于O的对称点为M，则直线PM为x=-a．

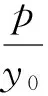
推论3 过定点Q(a,0)(a>0)的直线交抛物线y2=2px(p>0)于A，B两点，直线AO与直线x=-a交于点P，则直线PB∥x轴．

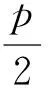
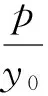
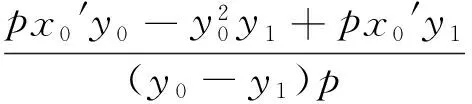
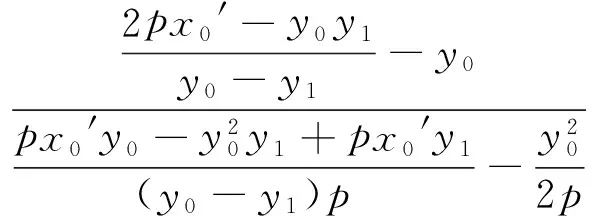
推论4 过定点Q(a,0)(a>0)的直线交抛物线y2=2px(p>0)于A，B两点，过点B作x轴的平行线交直线x=-a于点P，则直线AP经过原点O．

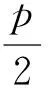
经过以上探究可以看出，这道竞赛题是在课本及高考题的基础上改编得来的．教材是集体智慧的结晶，对教学及各类考试有着导向作用，所以在习题教学中，要重视课本中的例习题，这样可以最大化的提高教学效率．