平面几何问题的解题对策

吴文尧

浙江省宁波市北仑中学 (315800)

平面几何问题的解题对策

吴文尧

浙江省宁波市北仑中学 (315800)

平面几何是学习平面解析几何和立体几何的基础,也是初中数学教学内容中的重点和难点，它还是高中数学竞赛必考内容.本文通过一道试题的解答，简要介绍解决平面几何问题的若干常用对策，供大家参考.

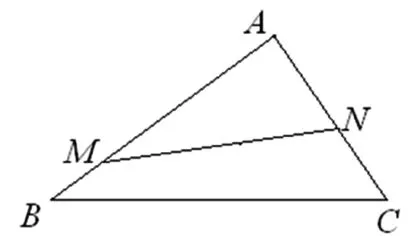
图1

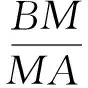
解题对策之一：解析法

分析：对于一个确定的ΔABC,M,N是两个动点,因此直线MN是动直线,若在直角坐标系中研究问题,易见本题是一个“证明动直线过定点”的问题；因此本题可按照解决证明动直线过定点的“套路”进行.

解答:以直线BC为x轴，线段BC的中垂线为y建立直角坐标系如图2，设B(-m,0)，则C(m,0)，

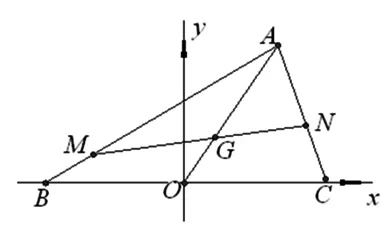
图2

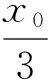
设M(x1,y1)，N(x2,y2)，

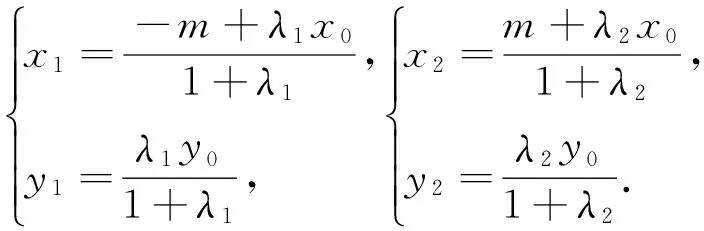
评注：(1)解析法的本质是用代数方法解决几何问题，它的最大优势是容易想到，且解题的过程可以程序化，其解题步骤可总结如下：

(A)建坐标,要合理——即建立合理坐标系，尽可能多的把图中的已知点安装在坐标轴上，还需照顾到图形的对称性.

(B)相关点,坐标化——求出问题涉及的图形中所有点的坐标.

(C)作运算,得结论——把要解决的几何问题化归为解析几何中的计算问题，明确运算目标，再“装腔作势”地进行合理的运算，得到所需的结论.

(2)本题比较自然的想法是：先求出直线MN及直线OA的方程，然后求其交点的坐标；但这种解决运算太繁，不具有可操作性.

解题对策之二:三角法

分析：不难发现，解决本题的关键是证明AG0=2G0O，即只需证明点G0的位置与λ1,λ2的取值无关，所以本题也可以看成是一个定值问题.注意到本题给出的图形与三角中的张角公式“使用环境”非常匹配，因此也可考虑用三角方法解决之.

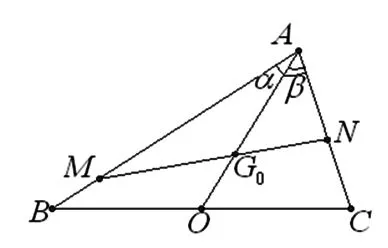
图3

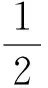
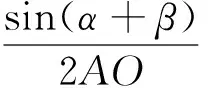
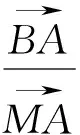
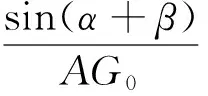
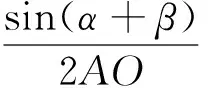
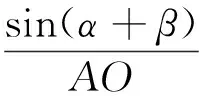
评注：三角法是解决平面几何问题的重要方法之一,通常可把平面几何的证明问题化归为三角函数的计算问题,思路自然,且有很强的可操作性.

解题对策之三:向量法

分析:要证明直线MN过ΔABC的重心G,即证明M,N,G三点共线,而平面向量在解决三点共线的问题时有较大的优势,因此也可把原问题化归为平面向量的运算问题来解决.

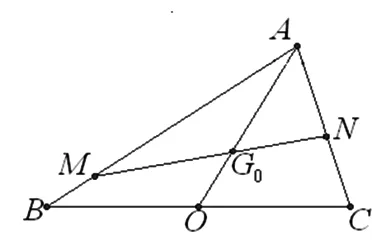
图4

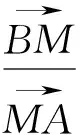
评注:“数形结合百般好，割裂分家万事休”(数学大师华罗庚先生语).数形结合思想是中学数学中最重要的思想方法之一，而平面向量是“数”和“形”之间天然的桥梁.上述解法的关键如何把M,G0,N三点共线这个条件“翻译”成关于λ,λ1,λ2的方程；其思路之自然，运算之简单，令人拍案叫绝.

解题对策之四:传统法.

分析：本题的解题目标是直线MN过ΔABC的重心，即证明直线MN分ΔABC的一条中线所成的比为2：1，即题目的条件和结论均涉及直线MN分ΔADC三边所成的比，所以可考虑利用梅涅劳斯定理解之.

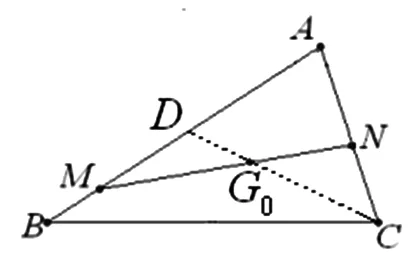
图5

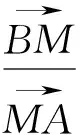
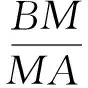
评注：传统方法的最大优点是运算简单、过程简捷,其不足之处是在应试中“想不到”；解决问题的过程其实是沟通条件和结论“感情”的过程，若注意对比条件和结论差异和共同点，合理地选择利用平面几何中的重要定理，通常还是能自然地想到解题的方法和思路.

学习高中数学后,与初中阶段相比,知识面更广了,看数学问题的观点也更高了,所以在解决平面几何问题时,解决问题的方法选择有很大的余地;根据题目的具体情况,结合自己的特长,一般能找到到合适的解决问题的途径.