Z2Z4-加性负循环码的对偶

胡万宝, 吴晶伶, 李萌

(安庆师范大学数学与计算科学学院,安徽 安庆 246133)

Z2Z4-加性负循环码的对偶

胡万宝, 吴晶伶, 李萌

(安庆师范大学数学与计算科学学院,安徽 安庆 246133)

在Z2Z4-加性码的基础上研究其循环码,进一步地引入其负循环码.通过建立Z2Z4下的正交关系,得出其对偶仍是一个Z2Z4负循环码;通过在Z2Z4码与Z4[x]-子模之间建立同构映射来刻画其负循环码的结构以及码的参数类型,并用构造性的方法推出了其对偶的最小生成集.这些结果,便于码元等参数的计算及其应用.

Z2Z4-加性码;Z2Z4-加性负循环码;对偶

1 引言

设Z2={0,1},Z4={0,1,2,3}分别为模2、模4剩余类环,则分别为环Z2和环Z4上的n维向量空间.Z4码即为的非空子集.二元线性码已为大家熟知,后A.R.Hammons,N.J.A.Sloane等人在文献[1]中研究了环Z4上的码,发现该码有很多优良的性质,特别是其Gray映射下的像为二元码.最近,T.Abualrub,I.Siap等人在二元、四元码的基础上在文献[2]中拓展了Z2Z4-加性循环码,得出了其在Gray映射下的像为四元码的结论.在文献[3-7]中,众多学者对Z2Z4码及其相关知识进行了研究及拓展.

本篇文章中,引入Z2Z4-加性负循环码的概念,也得到了与Z2Z4-加性循环码类似的好的参数.在第二节中,介绍Z2Z4-加性循环码的概念,其次引入Z2Z4-加性负循环码的概念,并类似于文献[2]定理12的步骤得出Z2Z4-加性负循环码的生成集.在第三节中,讨论了Z2Z4下的正交关系,结合剩余类环的相关知识,研究Z2Z4-加性负循环码的对偶,最后构造性的推出了Z2Z4-加性负循环码的对偶的多项式描述.

注1.1本文中所提及的β均为奇数.

2 Z2Z4-加性负循环码

定义2.1的一个非空集合C叫做Z2Z4-加性码,若C是的子群,即C同构于,其中γ,δ∈Z+.

因为任意Z2Z4-加性码C在加法下必封闭,所以在Z4下它也必定对于乘法封闭,即对于任意元素

其中,对任意 i=0,1,···,r−1,nai执行 mod 2运算,对任意 j=0,1,···,s−1执行 mod 4运算.

因而类似于文献[2]定义3,我们得到加性负循环码的定义如下.

定义2.2的子集C叫做Z2Z4-加性负循环码,若

(1)C是一个加性码,

(2)对任意码字

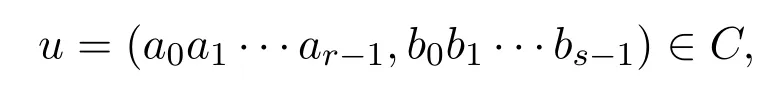
它的循环移位

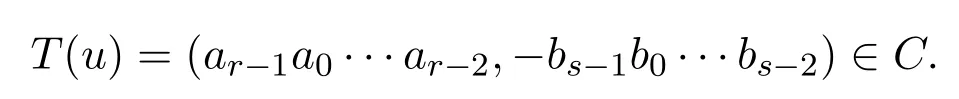
因为 C和Z4[x]/xβ+1是

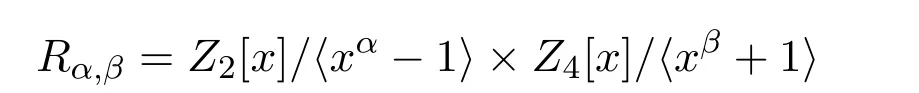
的Z4[x]-子模,定义以下映射

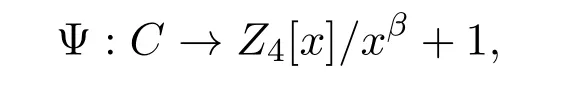
其中,

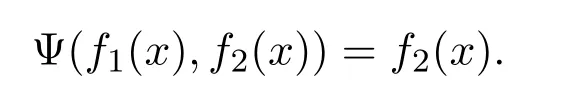
其中 a(x)|g(x)|(xβ+1)(mod 4).注意到

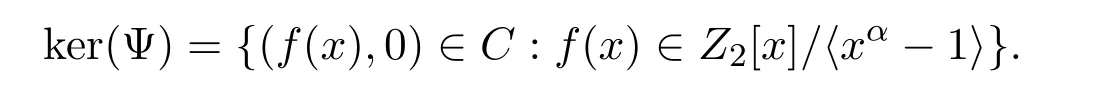
定义集合I为:

显然,I是一个理想,同时也是环Z2[x]/〈xα−1〉上的一个循环码.因此,由二元循环码的相关知识知 I=〈f(X)〉.对任意元素 (j(x),0)∈ ker(Ψ),有

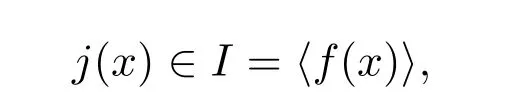
因此

所以

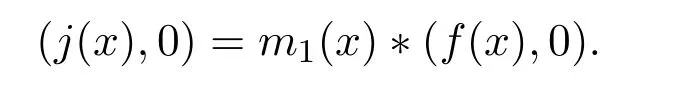
这就说明了ker(Ψ)是由一个形为(f(x),0)的元素生成的C的子模,其中

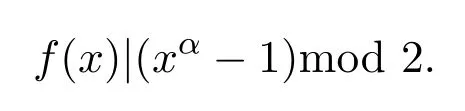
由第一同构定理知

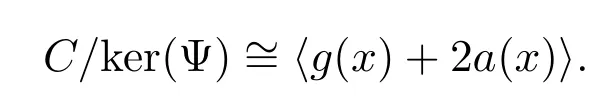
令 (l(x),g(x)+2a(x))∈C,使得

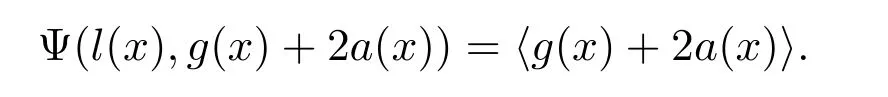
以上讨论内容就证明了任意Z2Z4-负循环码可由两个形为(f(x),0),(l(x),g(x)+2a(x))的元素生成,且它为Rα,β的 Z4-子模,即码C 中任意元素为

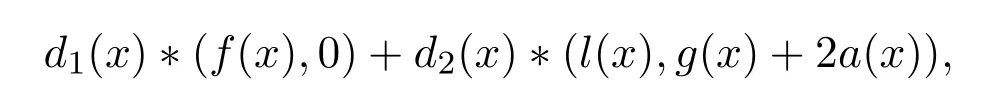
其中,d1(x),d2(x)为环Z4[x]上的多项式.事实上,d1(x)可被限制为环Z2[x]上的元素.记

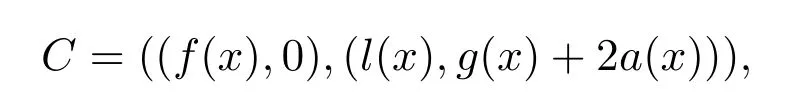
其中,f(x),l(x)为二元多项式,且a(x)|g(x)|(xβ+1)(mod 4).

定理2.1 令

是Rα,β中一个负循环码.其中

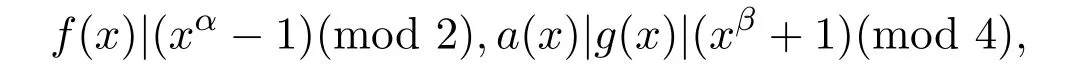
l(x)是一个二元多项式且满足

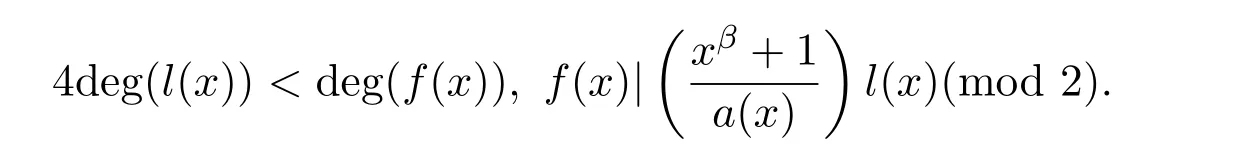
从而,C中共有2deg(hf)4deg(hg)2deg(b)个码字.

详细证明可类似于文献[2]定理13所得,这里就不再赘述.

3 Z2Z4-加性负循环码的对偶及其结构

定义3.1对任意码字

定义它们的內积为

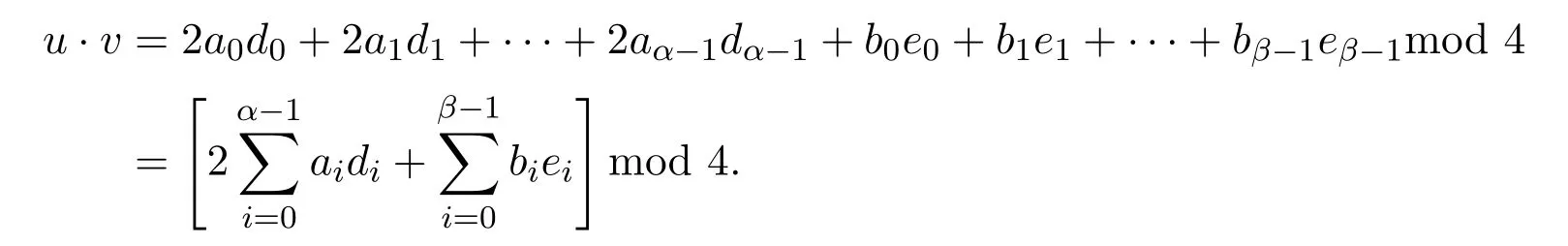
定义3.2若C是一个Z2Z4-加性负循环码,则C的对偶为:

定理3.1若C是一个Z2Z4-加性负循环码,则C⊥仍然是一Z2Z4-加性负循环码.

证明令C是一个Z2Z4-加性负循环码.假设

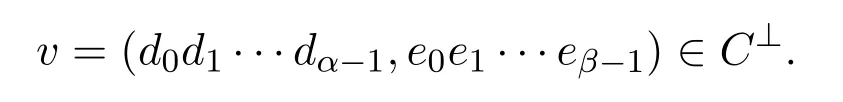
即要证T(v)∈C⊥.因为v∈C⊥,则对任意

要证T(v)∈C⊥,即证 u·T(v)=0.令

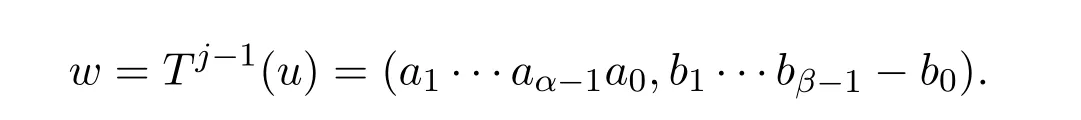
因为C是一个Z2Z4-负循环码,w∈C,所以

接下来讨论Z2Z4-加性负循环码的对偶的结构.在陈述和证明以下这些定理之前,首先强调中元素的正交关系.令

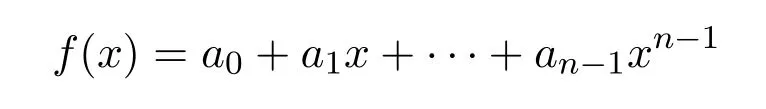
为环 Z2[x]/〈xn−1〉中的任一元素.注意,对任意 i=0,1,···,n−1,ai可能为零.从现在起,记

即若 an−1/=0,则 f∗(x)为 f(x)的互反多项式.由定义可知,f∗∗(x)=f(x).令

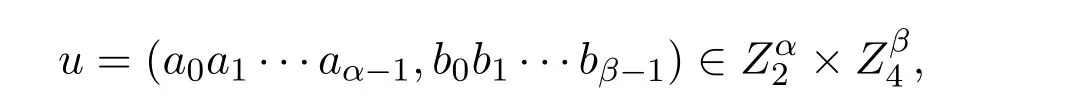
这个码字的循环移位

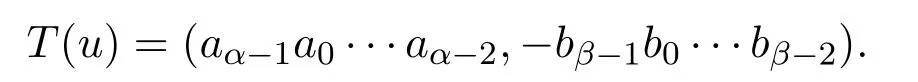
显然,集合 {u,T(u),T2(u),···,Tm−1(u)}包含了 u的所有循环移位,其中 m=lcm(α,2β).如上定义,回顾

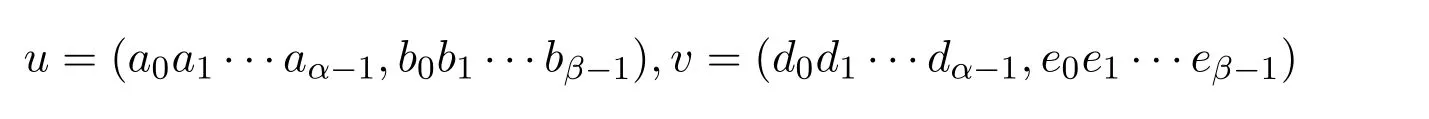
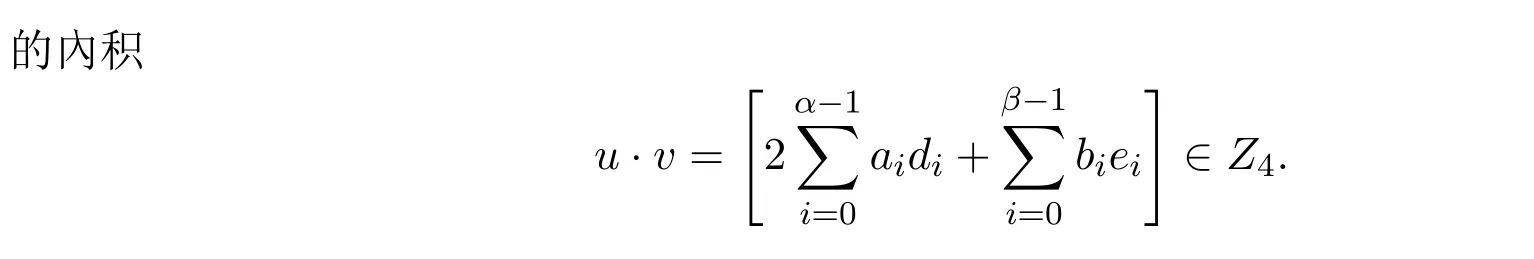
例3.1令

则

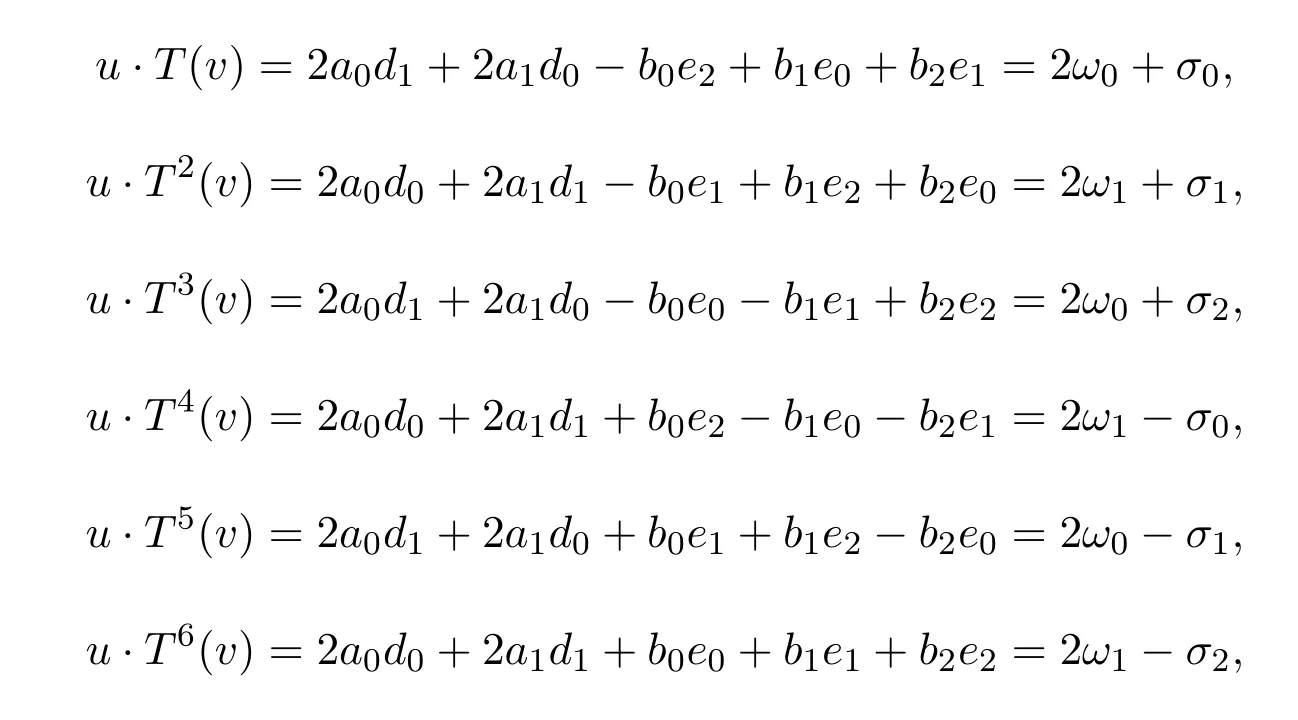
现在,令

构造多项式

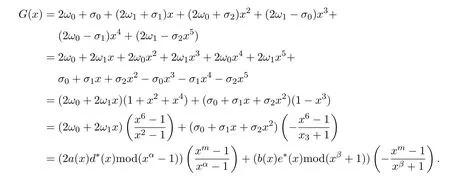
其中,m=lcm(α,2β).一般情况下,令

则

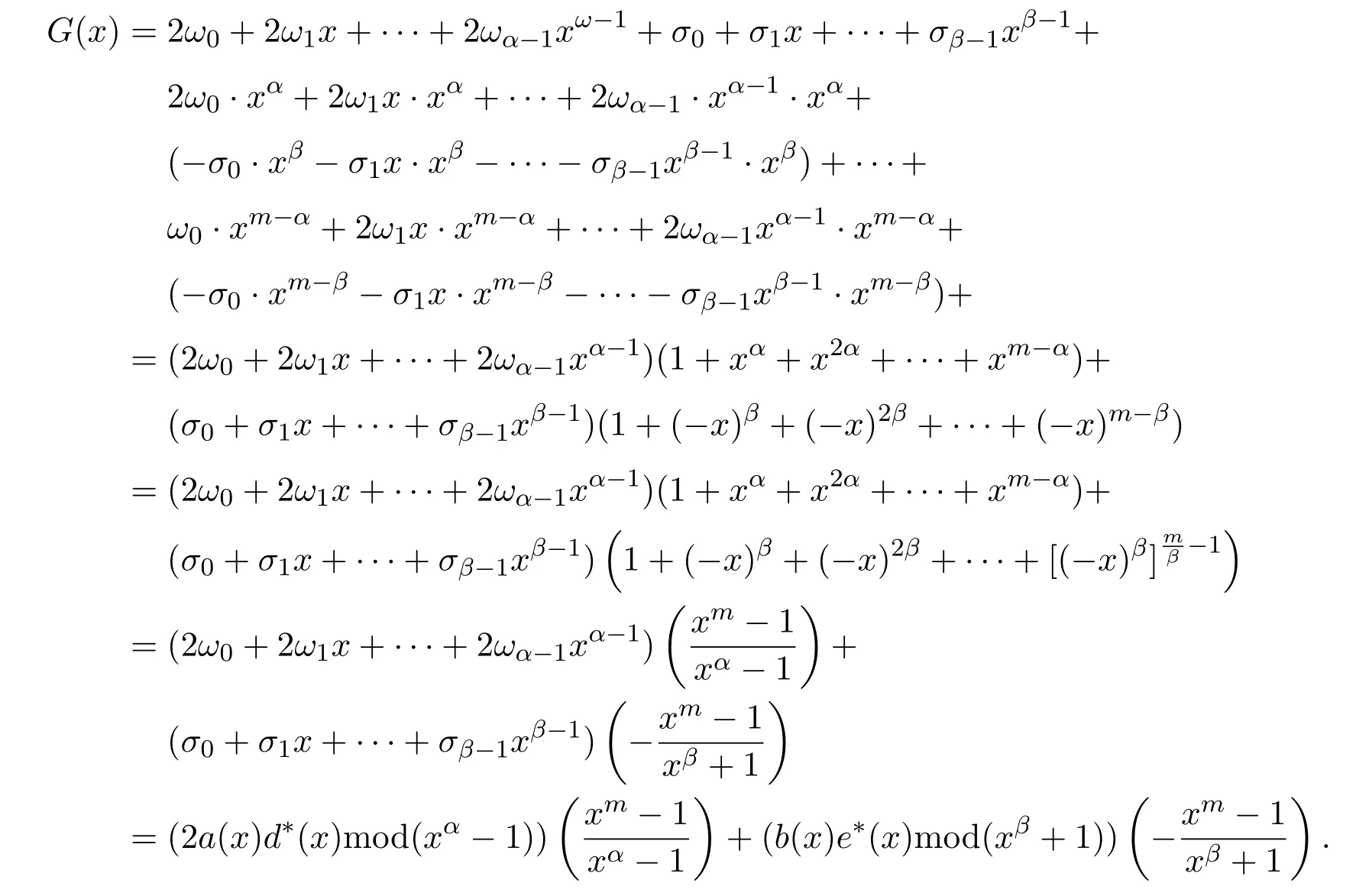
这就证明了以下定理.

定理3.2令

则u与v及其所有循环移位正交当且仅当G(x)等于

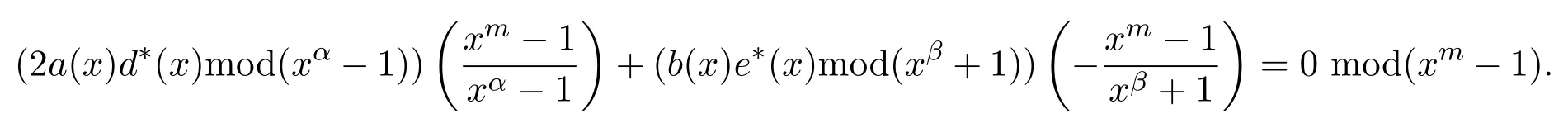
定理 3.3若 C是(α,β;k,k,k)型ZZ-加性码,则C 的标准矩阵为:

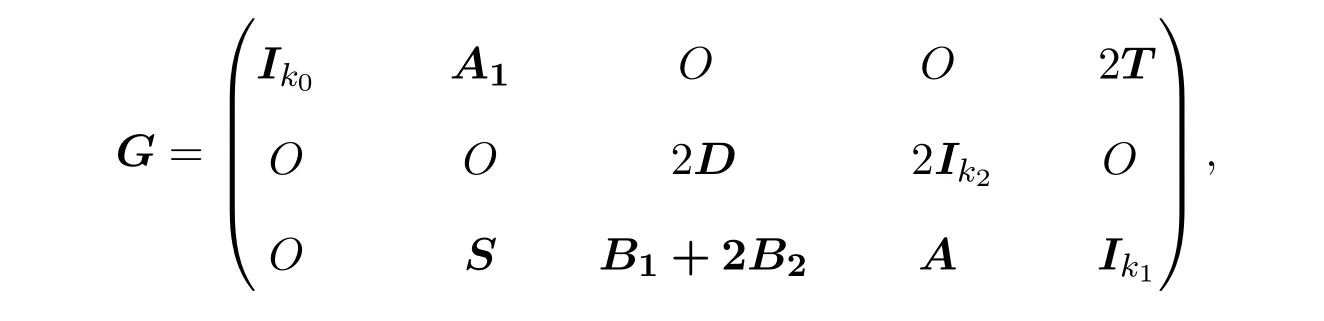
其中A,A1,B1,B2,D,S,T均为Z2上的矩阵.

定理3.4若 C是(α,β;k0,k1,k2)型Z2Z4-加性码,则对偶码C⊥的生成矩阵为:

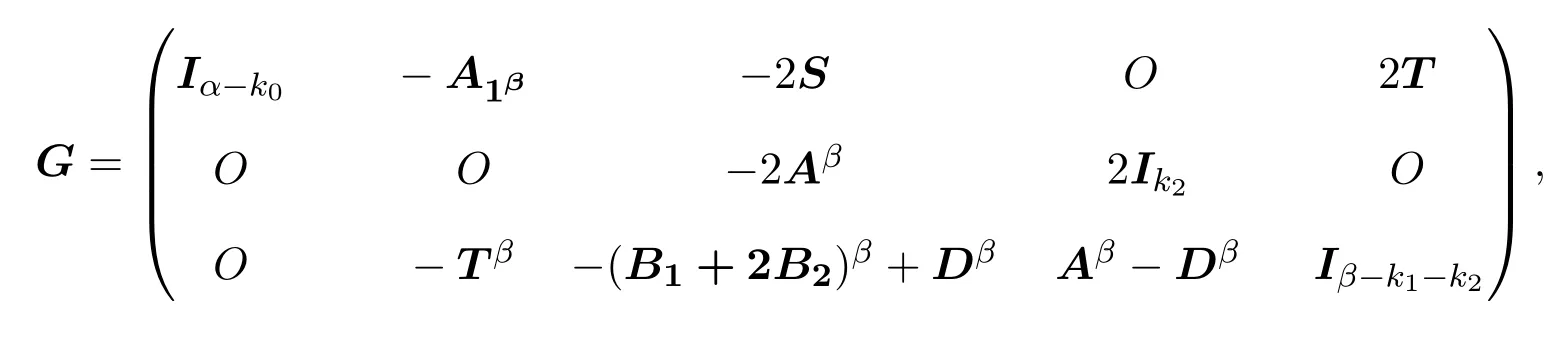
其中A,A1,B1,B2,D,S,T均为Z2上的矩阵.由C⊥的生成矩阵H,我们注意到C⊥是一个 (α,β;α−k0,β −k1−k2,k2)型加性码.

引理3.1令

是Rα,β中一个负循环码.

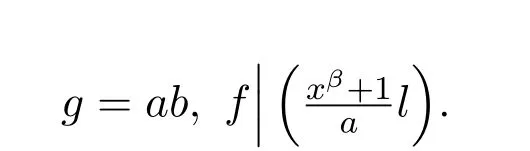
令

则d|d1,d2|b.

证明因为,所以因为

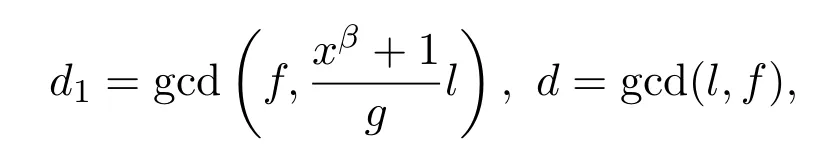
则显然

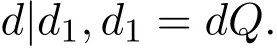
令

注意到

因为 f=d1d2,则 d1d2β1=d1v1b,即 d2β1=v1b.因为

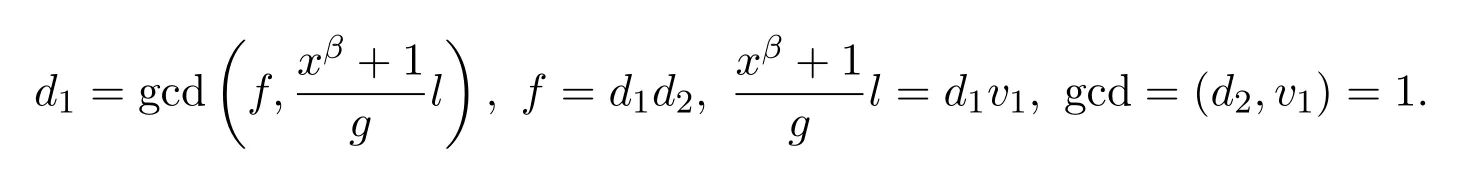
因此 d2s1+v1s2=1,两边同乘b,则

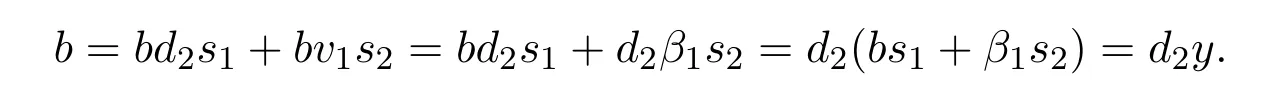
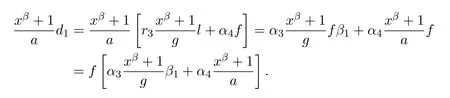
令

既得

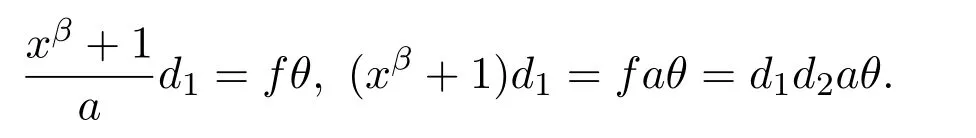
因此 xβ+1=d2aθ.因此,θ是 xβ+1的一个因子.又有 d=α1l+α2f,

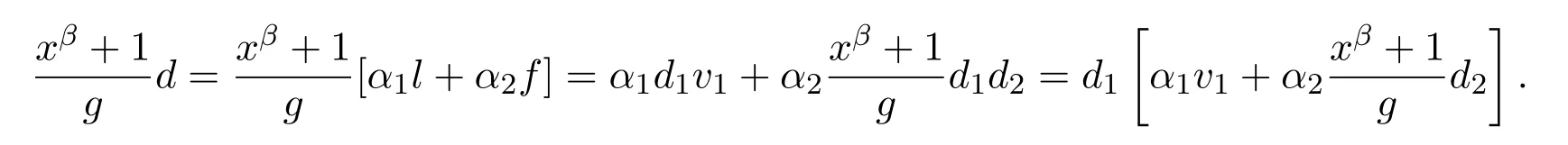
令

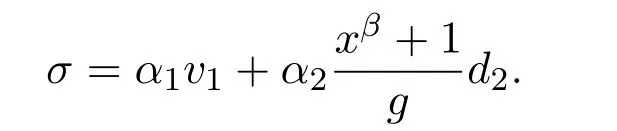
则

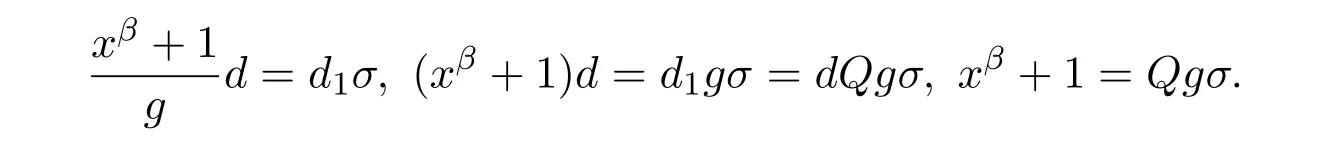
因此,σ是(xβ+1)的一个因子.

引理3.2令 C=〈(f,0),(l,g+2a)〉是 Rα,β中一个负循环码.其中

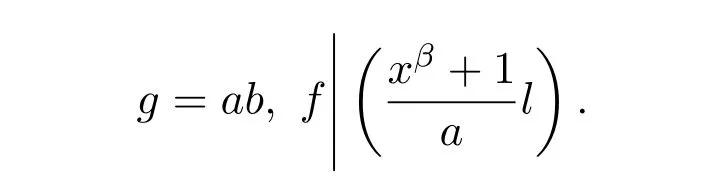
令

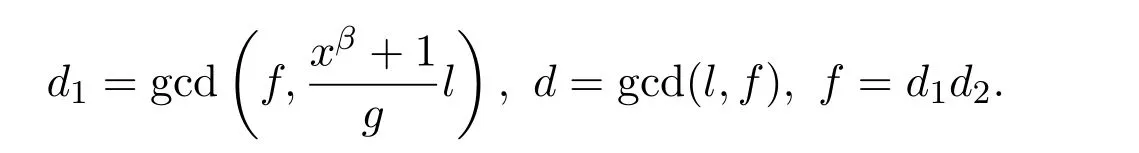
则码C正交于码

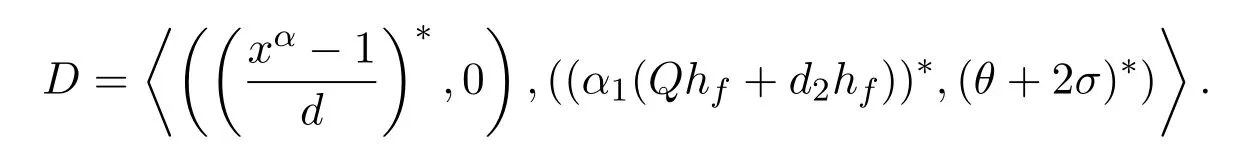
证明令C=〈(f,0),(l,g+2a)〉是一个Z2Z4-加性负循环码.其中

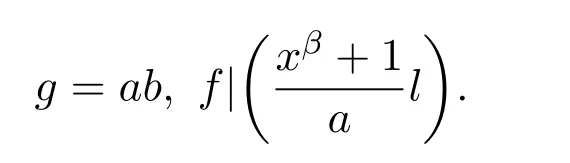
令

则

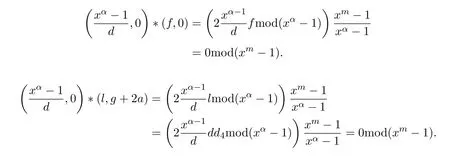
注意到

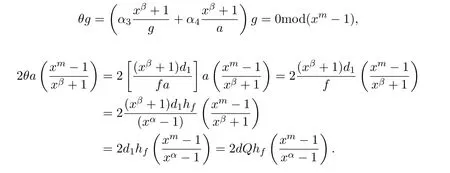
又

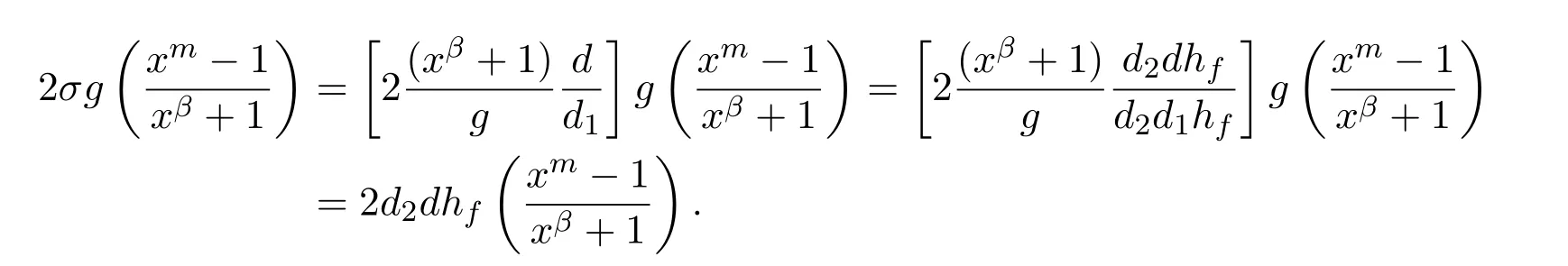
因此,

即证,码C正交于码D.

引理3.3令

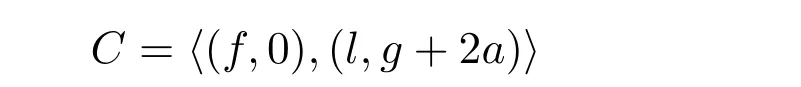
是Rα,β中一个负循环码.令

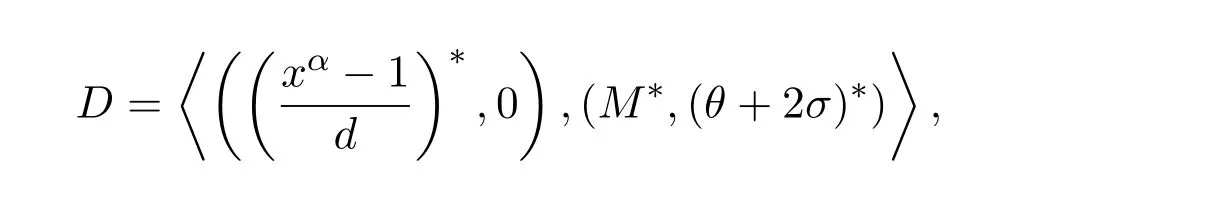
其中

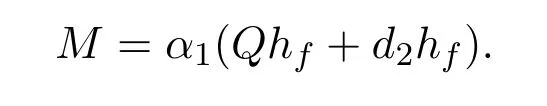
则

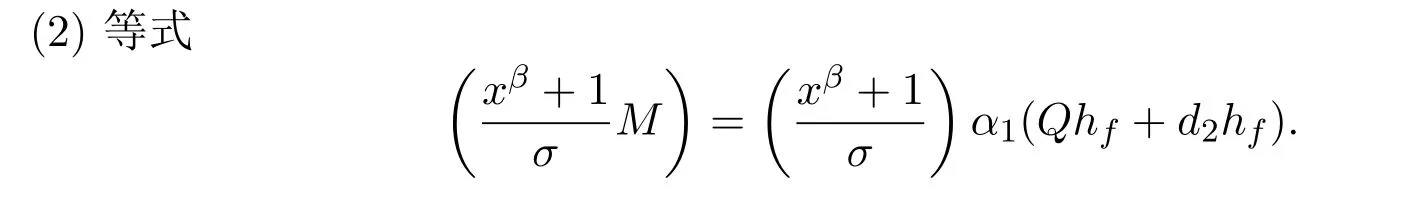
注意到

证明(1)显然的一个因子.因为

或

和σ是 (xβ+1)的因子.注意到

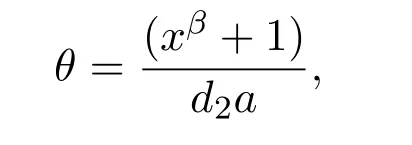
且

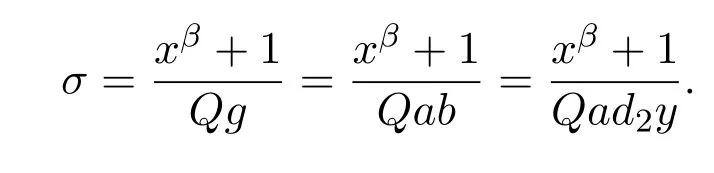
因此,

(2)等式

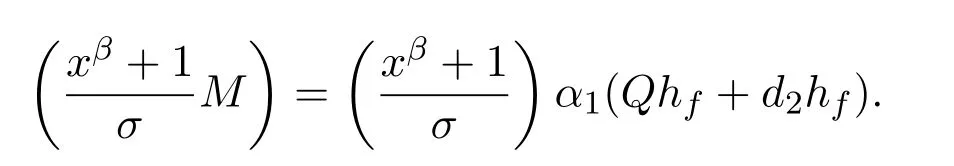
因此,

因此,

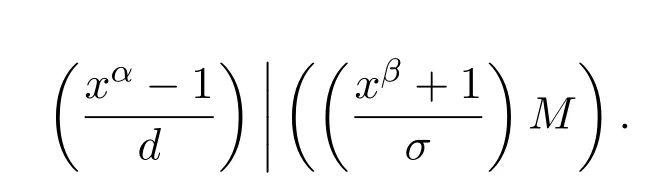
由此定理及定理2.1得以下定理.

引理3.4令

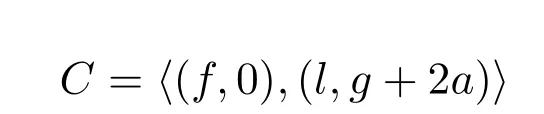
是Rα,β中一个负循环码.令

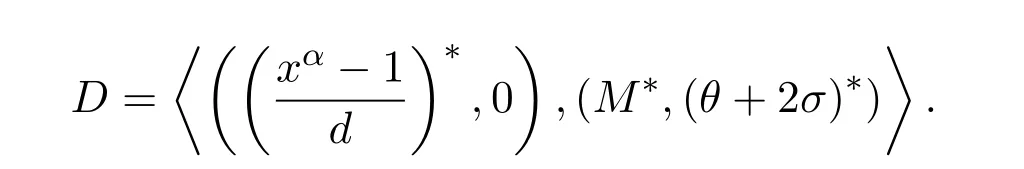
则 D 共有 2degd4(β−degθ)2(degθ−degσ) 个码字.

引理3.5令

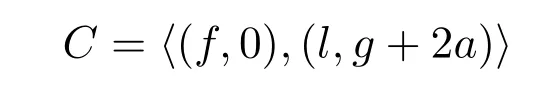
是Rα,β中一个负循环码.令

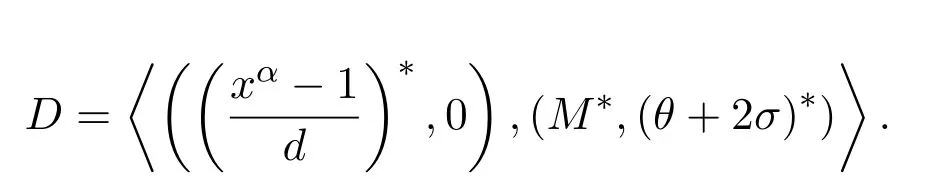
则|C||D|=2n.

证明我们知道

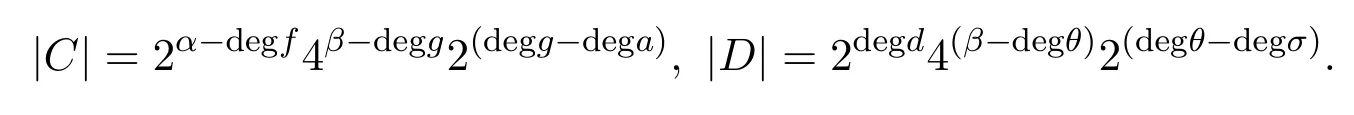
注意到

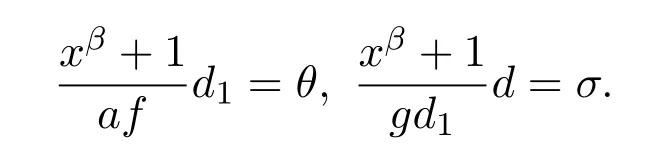
因此,

又

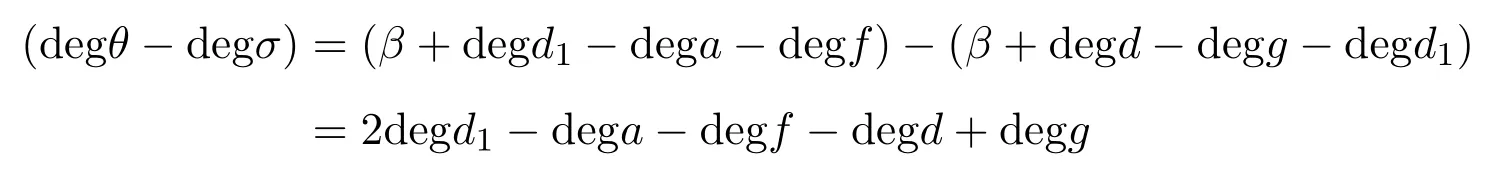
因此,|C||D|=2p.其中

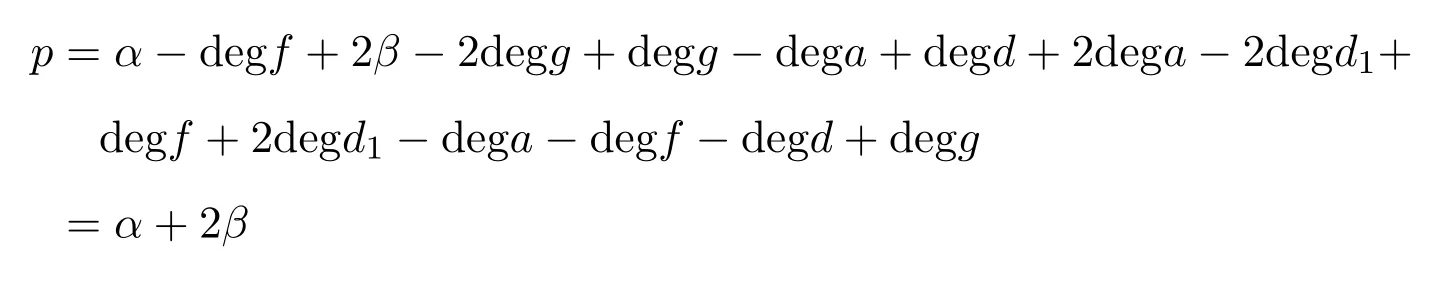
因此,

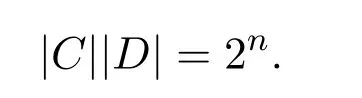
本文得到的主要定理如下:

定理3.5令

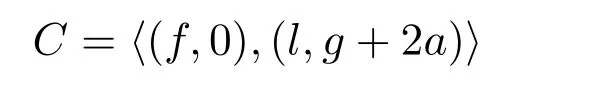
是一个Z2Z4-加性负循环码.则

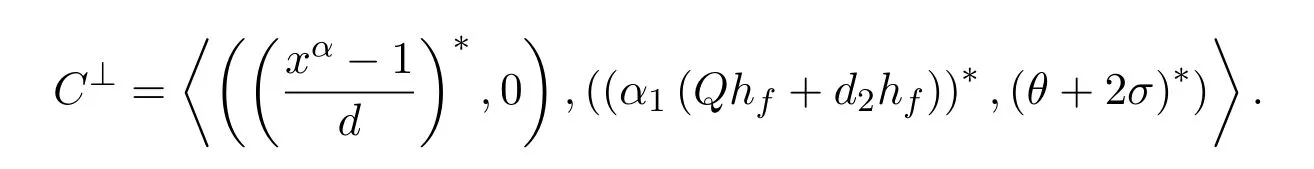
[1]Hammons A R,Kumar P V,Calderbank A R,et al.The Z4-linearity of Kerdok,Preparata,Goethals and related codes[J].IEEE Trans.Inf.Theory,1994,40(2):301-319.

[2]Abualrub T,Siap I,Aydin N.Z2Z4-cdditive cyclic codes[J].IEEE Trans.Inf.Theory,2014,60(3):1508-1514.

[3]Aydogua I,Abualrub T,Siap I.Z2Z2[u]-cyclic and constacyclic codes[J].IEEE Trans.Inf.Theory,2017,63(8):4883-4893.

[4]Pless V,Qian Z.Cyclic codes and quadratic codes over Z4[J].IEEE Trans.Inf.Theory,1996,42(5):1594-1600.

[5]Wolfmann J.Negacyclic and cyclic codes over Z4[J].IEEE Trans.Inf.Theory,1999,45(7):2527-2532.

[6]Borges J,Fernandez Cordoba C,Pujol J,et al.Z2Z4-linear codes:generator matrces and duality[J].Des.Codes Cryptogrrph,2009,54(2):167-179.

[7]Aydogdu I,Abualrub T,Siap I.On Z2Z2[u]-additive codes[J].International Journal of Compter Mathematics,2015,92(9):1806-1814.

Z2Z4-additive negacyclic codes

Hu Wanbao,Wu Jingling,Li Meng
(School of Mathematics and Computational Sciences,Anqing Normal University,Anhui246133,China)

Recently,on the basis of Z2Z44-additive codes,some scholars have studied its cyclic codes.As for a further comment,this paper introduced its negacyclic codes.By establishing the orthogonal relationship on Z2Z4,its dual is still a negacyclic codes can be proved.Through the establishment of isomorphic mapping between Z2Z4-code and Z4[x]-submodel,we can depict the structure of its negacyclic codes and the types of parameters.In addition,we give the generaters ofdual codes by constructive methods which can bring convenience to the calculation and application of the elements of codes.

Z2Z4-additive codes,Z2Z4-negacyclic codes,dual

O157.4

A

1008-5513(2017)05-0441-13

10.3969/j.issn.1008-5513.2017.05.001

2017-10-08.

国家自然科学基金(11626032,11601009).

胡万宝(1963-),博士,教授,研究方向：代数编码理论.

2010 MSC:11M06