关于Schrder路径计数的几个递推式的组合证明

尹鹏君

(北京工商大学理学院,北京 100048)

尹鹏君

(北京工商大学理学院,北京 100048)

利用 Schrder路径中不同类型的步的特点,研究不同初始高度的 Schröder路径,给出了Schrder路径计数的递推公式的组合证明.

Schrder 路径;小 Schrder 路径;初始高度

1 引言

Schröder[1]曾提出用括号划分一系列不同的字母的计数问题,并且给出了小Schröder数的生成函数σ(x),

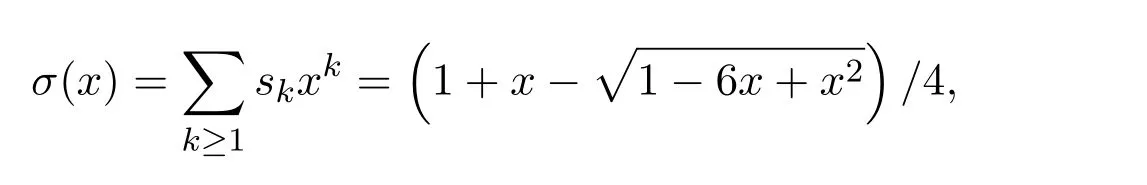
且满足

Shapiro和Sulanke[2]将(n+1)-多凸边形转化为平面树,并将平面树双着色,再构造平面树与 Schröder路径之间的双射,从而证明了大 Schrder数是小 Schrder数的两倍.Deutsch[3]将有序树分成两类,即矮灌木和高灌木,并利用这两种有序树在计数上相等且数量均为小 Schrder数的特性,给出了有序树与 Schrder路径的一一对应关系,进而巧妙、简练地得出了大 Schrder数与小 Schrder数的两倍关系.Huh和 Park[4]构造了长度为 n且可五着色的 Dyck路径与推广的 Schrder路径的双射,从而得出了推广的 Schröder路径的计数公式.Yan[5]构造了长度为 2n的 Schrder路径与 (2,3)-Motzkin路径之间的双射,给出了在限制不同类型步的条件下的 Schröder路径的计数公式.Song[6]定义了 m-Schröder路径,并给出了 m-Schröder路径的计数结果及证明.Chen和 Zhao[7]在 Shapiro和 Wang[8]的基础上,构造了长度为n的k-Motzkin路径与长度为 2n+2且不存在高度是偶数的水平步的 (k−2)-Schröder路径之间的双射.另外,Schröder数有很多组合结构.例如,长度为 2n且对每个峰进行二染色的Dyck路径的计数[3]、划分长度为(n+1)-多凸边形的计数[2]等.同样地,小Schröder数也存在很多对应的组合结构.例如,有n+1个叶子且不含有节点出度为1的有序树的计数[3]、划分长度为(n+2)-多凸边形的计数[3]及用括号划分n+1个不同字母的种类数[1]等等.本文主要从组合意义的角度,证明关于Schröder数的几个等式[9].首先,介绍一些定义.

定义1.1一条长度为 2n的 Schröder路径是由上升 U=(1,1)、下降 D=(1,-1)和水平H=(2,0)构成、起于点(0,0)止于点(2n,0)且只存在于x轴上或者x轴上方的路径.

定义1.2若路径中任意一步的两个端点的纵坐标中较大者为k,则称该步的高度为k.特别地,x轴上的水平步的高度为0.

定义1.3给定一条路径,如果这条路径的第一步的高度是0,则称这条路径是初始高度为0的路径;否则,如果从起点开始连续上升的步中最后一步的高度为k,则称这条路径是初始高度为k的路径,其中这些连续上升的步记为Uk,Uk中的第i步记为.长度为18且初始高度为4的Schröder路径,其中从起点开始连续上升的四步整体记为U4,并将这四步分别记为,如下图所示:

图1 长度为18且初始高度为 4的 Schröder路径

表1.1 长度小于12且不同初始高度k的Schröder路径的计数

定义 1.4长度为2n的小Schröder路径是一条x轴上不存在水平步的Schröder路径.

小 Schröder路径所组成的集合记为 Sn,其数量记为 sn.显然,sn等于小 Schröder数 (A001003[10]),即 1,1,3,11,45,···.长度为 2n且初始高度为 k的小 Schröder路径所组成的集合记为S(n,k),其数量记为s(n,k).长度小于12且不同初始高度k的小Schröder路径的计数如下表所示:

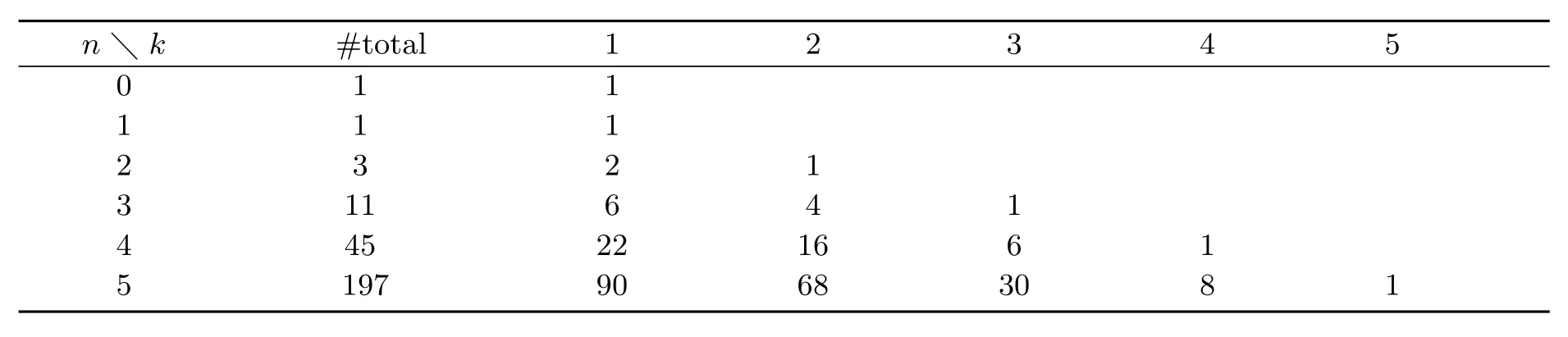
表1.2 长度小于12且不同初始高度k的小Schröder路径的计数

2 关于 Schrder路径的几个恒等式的组合证明

定理 2.1当n≥1,k≥0时,r(n,k)满足下列递推式:

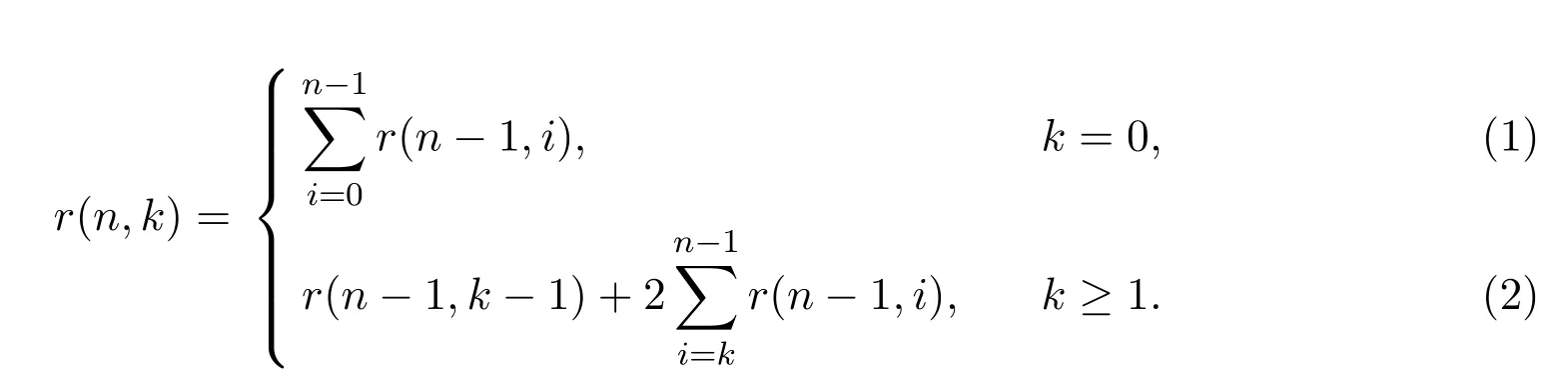
其中初始条件r(0,0)=1.

证明当k=0时,只需在所有长度为2(n−1)的 Schröder路径的起点插入一个 H 步,即可得到长度为2n且初始高度为0的Schröder路径.从而(1)式得证.

当k≥1时,采用数学归纳法.首先,给定一条长度为2m且初始高度为k的Schröder路径.

当m=1时,r(1,1)=1,显然,(2)式成立.

当m=n−1时,假设

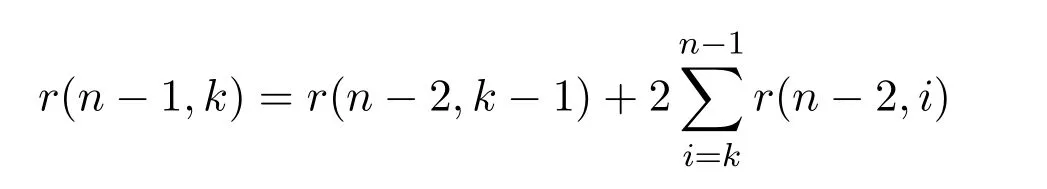
成立.

随着“互联网+”时代的到来，手机已成为人们生活中不可缺少的智能应用工具。随着各种智能化、人性化手机软件的开发，智能手机已经实现智能查询、导航、交互、支付等多种功能，并在向更加智能化的方向发展。而在大学生群体中，智能手机更是必备的应用工具。据相关调查发现，目前高校大学生几乎人人使用手机。除了生活中的应用外，智能手机以其便于携带、支持多媒体播放、实现信息互动的特性，使得高校学生在学习中也会普遍使用其上网查找学习资源，阅读电子书籍，开展个性化的自主学习，与老师、同学交流互动等。

当 m=n时,给定一条长度为 2(n−1)的 Schröder路径,若其初始高度为 k−1,则在后插入UD,从而得到相应的长度为2n且初始高度为k的Schröder路径;若其初始高度为j(k≤j≤n−1),则在后插入一个DU或者一个H.即得到长度为2n且初始高度为 k 的 Schröder路径.

显然,上述两种情况的过程均是可逆的.故等式(2)成立。

定理 2.2当n≥1,r(n,k)满足下列递推式:

其中初始条件r(0,0)=1.

证明首先,将长度为2n且初始高度为0的Schröder路径的第一步进行二染色,该步分别记为H1、H2,且将染色后的路径组成的集合记为R2(n,0).

给定集合R2(n,0)中的任意一条路径 P,考虑以下变换.若路径 P的第一步为 H1,则将H1变为UD;若路径P的第一步为H2且第二步为H,则删除H2;若路径P的第一步为H2且第二步为U,则将H2U变为UH.由于R(n,1)中的路径只能以UD或UH为起始步,而R(n,0)中的路径只能以H 为起始步,故上述变换可逆.从而(2.2−1)式成立.

定理2.3当n≥1,k≥1时,r(n,k)满足下列递推式:其中初始条件r(0,0)=1.

第一种情况,给定长度为2n且初始高度为k+1的Schröder路径时,该路径的第k+2步可能是D或H,分别将变为DU,变为HU,其它步保持不变.

第二种情况,给定长度为 2 (n−1)且初始高度为 k 的 S chröder路径,在后插入 D U或H.

第三种情况,给定长度为2(n−1)且初始高度为 k −1的Schröder路径中,在后插入UD.

反之,若给定一条长度为2n且初始高度为k的Schröder路径.根据该路径的第k+1、k+2步,可以将Schrder路径分成以下六种:

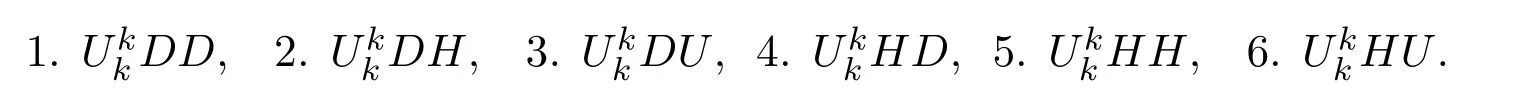
如下图所示:

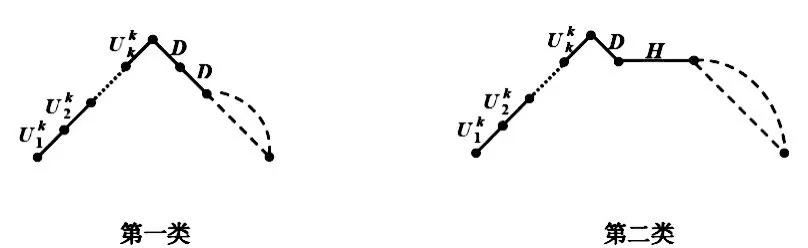
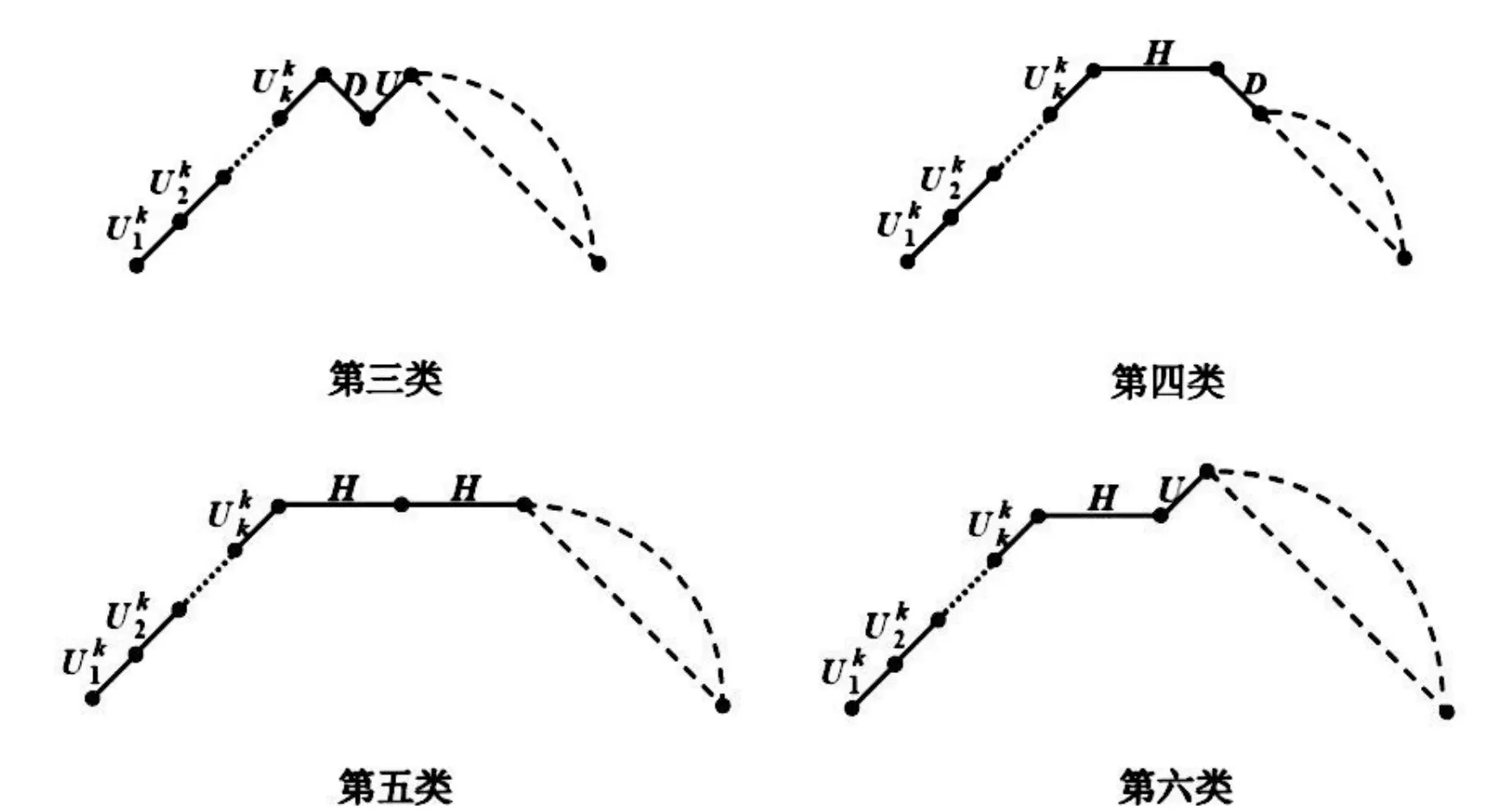
图2 长度为2n且初始高度为k的六种不同的Schröder路径(k/=0)

综上,等式(4)成立.

推论2.1当n≥1,k≥1时,s(n,k)有下式成立:

其中初始条件s(0,0)=1.

推论2.2当时,s(n,k)有下式成立:

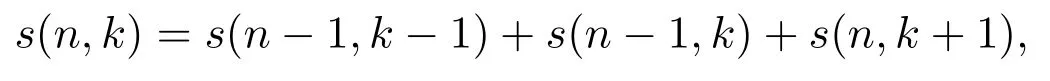
其中初始条件s(0,0)=1.

[1]Schröder E.Vier combinatorische Probleme[J].Z.fur Math.Physic.,1870,15:361-376.

[2]Shapiro L W,Sulanke R A.Bijections for the Schröder numbers[J].Mathematics Magazine,2000,73(5):369-376.

[3]Deutsch E.A bijective proof of the equation linking the Schröder numbers,little and small[J].Discrete Math.,2001,241:235-240.

[4]Huh J S,Park S K.Generalized small Schröder numbers[J/OL].Electronic J.Combin.,2015[2017-07].http://www.combinatorics.org.

[5]Yan S H F.From(3,2)-Motzkin paths to Schröder paths[J/OL].J.Integer Sequences,2007[2017-07].http://www.emis.de/journals/JIS/vol10.html.

[6]Song C W.The generized Schröder theory[J/OL].Electronic J.Combin.,2005[2017-07].http://www.combinatorics.org.

[7]Chen Z J,Zhao S.Two bijections on weighted Motzkin paths[J].Communications In Mathematical Research,2017,33(2):149-159.

[8]Shapiro L W,Wang C J.A bijection between 3-Motzkin paths and Schröder paths with no peak at odd height[J/OL].J.Integer Sequences,2009[2017.07].http://www.emis.de/journals/JIS/vol12.html.

[9]Pergola E,Sulanke R A.Schröder triangles,paths,and parallelogram polyominoes[J].J.Integer Sequences,1998[2017-07].http://www.emis.de/journals/JIS/vol1.html.

[10]Sloane N J A.The On-Line Encyclopedia of Integer Sequences[EB/OL].The OEIS Foundation Inc.,2014[2017-07].http://oeis.org.

The combinatorial proofs of several recurrences about the enumeration of Schröder paths

Yin Pengjun
(School of Mathematics,Beijing Technology and Business University,Beijing 100048,China)

By analyzing the characteristics of di ff erent steps in the Schröder paths,we studied the Schröder paths with di ff erent initial height and provided the combinatorial proofs of several recurrences of the enumeration of Schröder paths.

Schröder path,little Schröder path,initial height

O157.1

A

1008-5513(2017)05-0530-06

10.3969/j.issn.1008-5513.2017.05.011

2017-08-03.

国家自然科学基金(11601020;11501014);北京市委组织部优秀人才项目(2013D005003000012);2017商科特色项目(19005757053).

尹鹏君(1992-),硕士研究生,研究方向：组合计数.

2010 MSC:05A15