拓扑剩余格_参考网

拓扑剩余格

2017-11-01贺永春练利锋

纯粹数学与应用数学 2017年5期

关键词：滤子榆林代数

贺永春, 练利锋

(1.榆林学院数学与统计学院,陕西榆林 718000;2.重庆第二师范学院数学与信息工程学院,重庆 400065)

拓扑剩余格

贺永春1, 练利锋2

(1.榆林学院数学与统计学院,陕西榆林 718000;2.重庆第二师范学院数学与信息工程学院,重庆 400065)

利用剩余格L中滤子系统

诱导的拓扑τF,证明了(L,τF)是拓扑剩余格,给出拓扑剩余格(L,τF)中任意一个非空集合的闭包的表达形式,并且在给定的一些特殊的条件下证明了(L,τF)是Hausdor ff空间.

拓扑剩余格;滤子系统;Hausdor ff空间

1 引言

剩余格已成为模糊逻辑中比较理想的代数框架,是研究其他代数结构的重要工具.关于剩余格的研究,读者可以参考文献[1-4].代数和拓扑是数学的两个基础的领域,它们虽然是相对独立的,但是在数学的高领域的研究中有着紧密的联系,如群表示论、代数几何、代数拓扑、拓扑代数等.自从剩余格理论建立以来[5],关于剩余格在模糊代数理论的研究得到了广泛的关注,但是在拓扑理论方面研究甚少.有关逻辑代数上拓扑结构的研究,请读者参照文献[6,8].基于此,研究拓扑剩余格是有意义的.

2 预备知识

定义 2.1[1-2]一个(2,2,2,2,0,0)型的代数(L,∧,∨,⊙,→,0,1)若满足下列条件:对任意的x,y,z∈L,

(i)(L,∧,∨,0,1)是有界格,0,和1分别为L的最小元和最大元;

(ii)(L,⊙,1)是可换幺半群;

(ii)x⊙y≤z当且仅当 x≤y→z;则称(L,∧,∨,⊙,→,0,1)为一个剩余格.

本文中,如没有特别声明,剩余格(L,∧,∨,⊙,→,0,1)简记为L.

命题 2.1[4]若L是一个剩余格,则以下各条可证：对任意的x,y,z∈L,

(R1)1→x=x,x→1=1,

(R2)x≤y当且仅当x→y=1,

(R3)如果x≤y,则有y→z≤x→z,z→x≤z→y以及x⊙z≤y⊙z,

(R4)x⊙(x→y)≤y,

(R5)x⊙y≤x∧y,x≤y→x,

(R6)x→(y→z)=(x⊙y)→z=y→(x→z),

定义 2.2[2,3]设F是L的一个非空子集,若F满足以下条件:

(i)x,y∈F蕴含x⊙y∈F;

(ii)x∈F且x≤y蕴含y∈F；则称F是L的滤子.

剩余格L的子集F称为推导系统是指F满足以下条件:

(i)1∈F;

(ii)x,x→y∈F蕴含y∈F.容易验证在剩余格中滤子和推导系统是一致的.记剩余格L中全体滤子的集合为F(L).

定义 2.3[6]偏序集(D,≤)称为定向集,如果对任意x,y∈D,存在z∈D使得

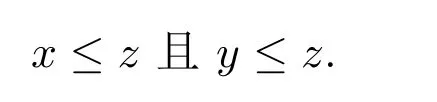
定义 2.4[7]设τ是L上的拓扑.若L中的每个运算都关于τ连续,则称序对(L,τ)为拓扑剩余格.

3 主要结果及其证明

定义 3.1[12]设Λ是定向集以及

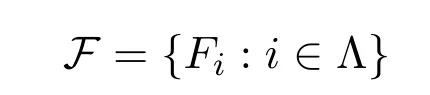
是剩余格L的一族滤子.对任意的 i,j∈Λ,如果i≤j蕴含Fj⊆Fi,则称 {Fi:i∈Λ}为 L的滤子系统（或简记为系统）.

引理 3.1设F={Fi:i∈Λ}是L的系统.则L中存在拓扑τ具有基

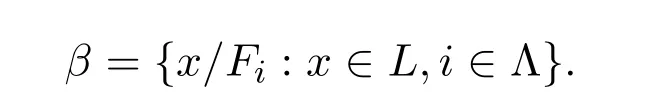
证明设

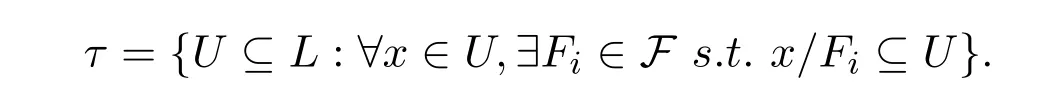
下面证明τ是L上的拓扑.显然∅,L∈τ.设

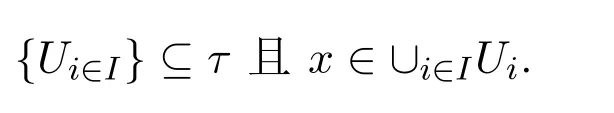
则存在i∈I使得x∈Ui.由于 Ui∈τ,从而存在Fj∈F 使得x/Fj⊆Ui.因此有

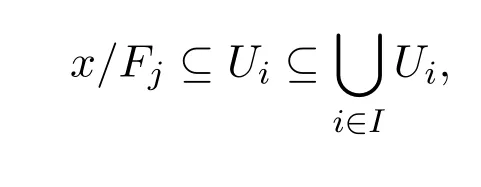
故

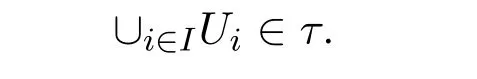
假设 Ui,Uj∈τ.下面我们证明 Ui∩Uj∈τ.设x∈Ui∩Uj.则存在Fk,Fl∈F 使得

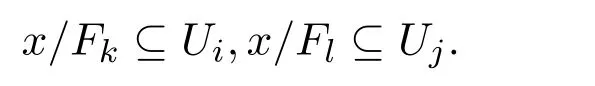
由于Λ是定向集,存在h∈Λ使得k,l≤h.因此有

不难证明

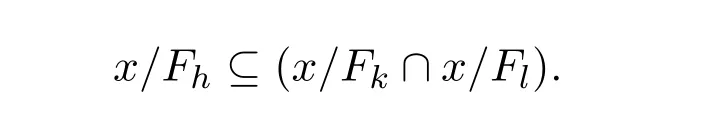
故有

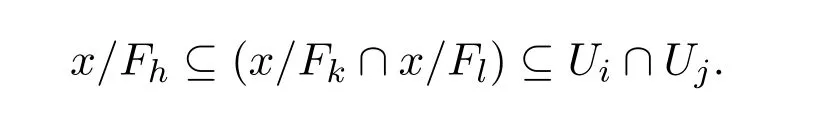
任取U∈τ以及x∈U,则存在Fx∈F使得x/Fx⊆U.因此有

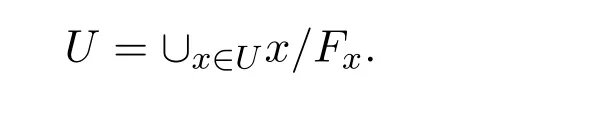
所以β是τ的基.

注 3.1本文主要讨论剩余格L中滤子系统

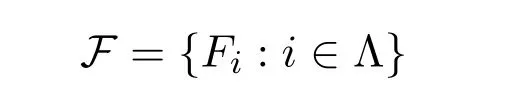
诱导的拓扑

(简记为τF)的拓扑性质.如果没有特殊说明,本文总假设τF是由滤子系统

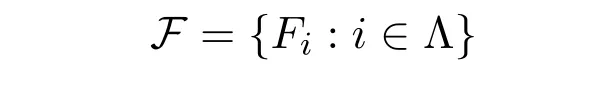
诱导的拓扑.

众所周知剩余格L中的任意一个滤子F都可以诱导L上的一个同余关系θF,这里θF定义为 (x,y)∈θF当且仅当x→y∈F,y→x∈F.

定理3.1设

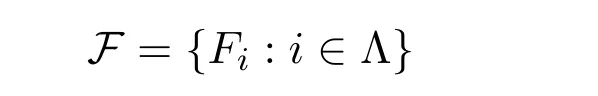
是L的系统.则(L,τF)是拓扑剩余格.

证明由引理知 (L,τF)是拓扑空间.下面只需要证明对L中运算 ∗∈{∧,∨,⊙,→}以及

映射f∗:L×L→L定义为

是连续的.由于(L,τF)具有基

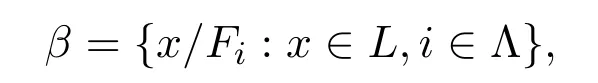
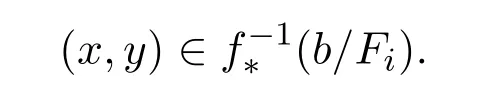
则有 x∗y∈b/Fi,显然有

是L×L中点(x,y)的开领域.下面证明

则 u∈x/Fi且 v∈y/Fi,即 (u,x)∈θFi以及 (v,y)∈θFi,这里 θFi是由 Fi诱导的同余.因此有

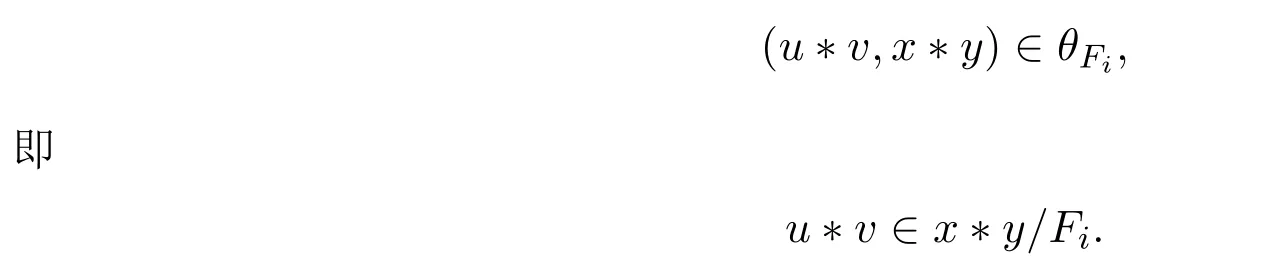
由x∗y∈b/Fi,可得到u∗v∈b/Fi.故有

下面给出拓扑剩余格(L,τF)中任意一个非空集合的闭包的具体表达形式.

定理 3.2设(L,τF)是拓扑剩余格以及S是L中的非空子集.则

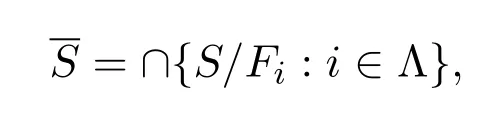
这里S是S的拓扑闭包,

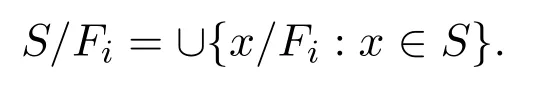
证明设x∈L以及

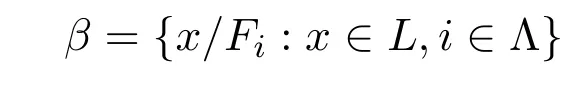
是τF的基.则有 x∈,

⇔对x的任何领域U,总有

定理 3.3(L,τF)是 Hausdor ff空间当且仅当

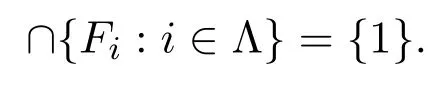
证明设(L,τF)是 Hausdor ff空间.则

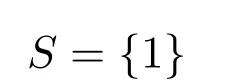
是闭集.由引理得

反之,设

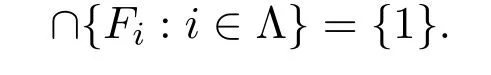
任取 x/=y,则有

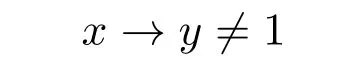
或者

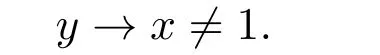
不失一般性,设

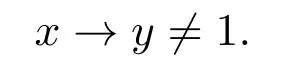
由假设

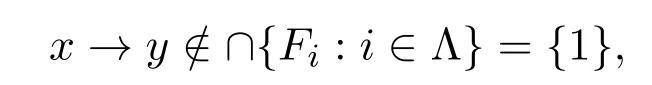
则存在λ∈Λ使得x→y/∈Fλ.因此x/∈y/Fλ,则有

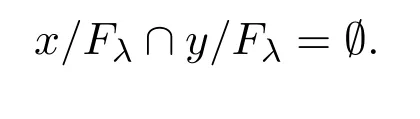
[1]Ward M,Dilworth P R.Residuated lattice[J].Transactions of the American Mathematical Society,1939,45(1939):335-354.

[2]Piciu D.Algebras of Fuzzy Logic[M].Ed.Craiova:Universitaria,2007.

[3]裴道武.Ro-代数中的蕴涵滤子与同余关系[J].西安联合大学学报,2000,3(4):24-29.

[4]Kowalski T,Ono H.Residuated Lattices:An Algebraic Glimpse at Logic Without Contraction[M].New York:Springer,2001.

[5]Davey B A,Priestley H A.Introduction to Lattice and Order[M].Cambridge:Cambridge University Press,2002.

[6]Haveshki M,Eslami E,Borumand Saeid A.A topology induced by uniformity on BL-algebras[J].Math.Log.Q.,2007,53(2):162-169.

[7]Zahiri O,Borzooei R A.Topology on BL-Algebras[J].Fuzzy Sets.Syst.,2016,289(3):137-150.

[8]熊金城.点集拓扑学讲义[M].3版.北京:高等教育出版社,2003.

Topology on residuated lattices

He Yongchun1,Lian Lifeng2
(1.School of Mathematics and Statistics,Yulin University,Yulin 718000,China 2.School of Mathematics and Information Engineering,Chongqing University of Education,Chongqing 400065,China)

In this paper,by using a special family of fi lters on a residuated lattice L,we construct a topology τFon L,show that(L,τF)is a topological residuated lattice, fi nd the closure of any subsets of L and obtain some conditions under which that(L,τF)is a Hausdor ffspace.

topological residuated lattice,system of fi lters,Hausdor ffspace