剩余格的犹豫模糊滤子理论*

彭家寅

内江师范学院 数学与信息科学学院，四川 内江 641199

剩余格的犹豫模糊滤子理论*

彭家寅+

内江师范学院 数学与信息科学学院，四川 内江 641199

将犹豫模糊集概念应用于剩余格的滤子理论中，提出了剩余格的犹豫模糊滤子、犹豫模糊蕴涵滤子、犹豫模糊正定蕴涵滤子、犹豫模糊MV-滤子及犹豫模糊正规滤子的概念，研究了它们的性质，讨论了它们之间的关系，获得了它们的若干等价刻画。给出了犹豫模糊集成为犹豫模糊滤子，及犹豫模糊滤子成为犹豫模糊（正定蕴涵、MV、正规）蕴涵滤子的条件。探究了各种犹豫模糊滤子与其对应的水平滤子之间的关系，建立了剩余格的犹豫模糊Boolean滤子和犹豫模糊正规滤子的扩张定理。

剩余格；犹豫模糊集；犹豫模糊（蕴涵、正定蕴涵、MV、正规）滤子；犹豫模糊集的水平集

1 引言

1939年，Ward和Dilworth引入剩余格的概念[1]。此后，Hájek以Lukasiewicz公理系统为背景将剩余格引入模糊逻辑研究中[2]，把剩余格作为一个非常基本的语义代数，使许多逻辑代数都含有剩余格的代数结构，如格蕴涵代数[3]、BL-代数[1,4]、MV-代数[5]、MTL-代数[6]、R0代数[7]等。滤子理论在逻辑代数研究中扮演着重要的角色。从逻辑观点看，推理系统中可证公式集合就可以通过滤子这种子结构来描述，基于不确定信息的相应代数子结构就对应着模糊滤子。从代数看，滤子之集的性质直接影响相应逻辑代数的结构性质，它是研究代数结构的重要工具之一。因此，建立剩余格的滤子理论对于研究上述逻辑代数常见性质是非常有意义的。目前，BL-代数和剩余格的滤子理论得到了深入的研究[8-12]。

自Zadeh于1965年提出模糊集[13]的概念以来，模糊集已成为处理模糊信息的有效工具，并被广泛地用于各个学科领域。随后，模糊集的一些拓展理论被提出，如区间值模糊集[14]、直觉模糊集[15]、n-型模糊集[16]等。最近，Torra[17]引入了犹豫模糊集的概念，解决了建立隶属度的困难：不是因为误差或一些可能值的可能性分布，而是由于人们在一些不同的值之间犹豫导致的。犹豫模糊集作为模糊集的另一种推广，允许元素的隶属度为0与1之间一些可能值的一个集合，因此就模糊集或其经典推广而言，它提供了一个关于人们描述对对象的偏好程度犹豫的更准确表示。目前，犹豫模糊集除被应用于一些实际问题的决策领域外[18-22]，也被应用于某些代数结构的研究中[23-25]。

本文为进一步研究剩余格代数的结构特征，将犹豫模糊集应用于剩余格中，初步建立起剩余格的犹豫滤子理论。引入剩余格的几种犹豫模糊滤子的概念，讨论它们的基本性质及其间的关系，给出它们的一些等价刻画，研究几种犹豫模糊滤子的扩张性质。讨论由犹豫模糊集构成犹豫模糊滤子，及由犹豫模糊滤子构成犹豫模糊（蕴涵、正蕴涵、MV-滤子）正规滤子的条件。

2 预备知识

定义1[1]剩余格是一个(2,2,2,2,0,0)型代数结构L=(L,∨,∧,⊗,→,0,1)且满足如下公理。

（C1）(L,∨,∧,0,1)是一个有界格。

（C2）(L,⊗,1)是一个以1为单位元的交换半群。

（C3）(⊗,→)为伴随对，即∀x,y,z,w∈L：

（R1）若x≤y且z≤w，则x⊗z≤y⊗z。

（R2）若x≤y，那 么y→z≤x→z并 且z→x≤z→y。

（R3）x⊗y≤z当且仅当x≤y→z。

文中除特殊声明，L总表示一个剩余格。

命题1[1]在每个剩余格L中，下列结论成立。

对任意x,y,z∈L，有：

（P1）(x⊗y)→z=x→(y→z)。

（P2）x→(y→z)=y→(x→z)。

（P3）0′=1，1′=0，x′=x‴，x≤x″，这里x′=x→0。

（P4）x∨y→z=(x→z)∧(y→z)。

（P5）x⊗x′=0。

定义2[9]（1）剩余格L的非空子集F叫作L的一个滤子，如果它满足下列条件：

（F1）(∀x,y∈L)(x,y∈F⇒x⊗y∈F)；

（F2）(∀x,y∈L)(x∈F,x≤y⇒y∈F)。

（2）剩余格L的非空子集F叫作L的一个蕴涵滤子，如果它满足下列条件：

（F3）1∈F；

（F4）(∀x,y,z∈L)(z,z→((x→y)→x)∈F⇒x∈F)。

（3）剩余格L的非空子集F叫作L的一个正定蕴涵滤子，如果它满足条件（F3）和条件（F5）：

（F5）(∀x,y,z∈L)(z→(x→y),z→x∈F⇒z→y∈F)。

（4）剩余格L的滤子F叫作L的一个Boolean滤子，如果它满足条件：

（F6）(∀x∈L)(x∨x′=1)。

（5）剩余格L的滤子F叫作L的一个MV-滤子，如果它满足条件：

（F7）(∀x,y∈L)(y→x∈F⇒((x→y)→y)→x∈F)。

（6）剩余格L的滤子F叫作L的一个R-滤子，如果它满足条件：

（F8）(∀x∈L)(x″→x∈F)。

定义3[17]设X为一个参考集，从X到[0,1]的幂集P([0,1])上的一个映射ϕ∶X→P([0,1])叫作X上的一个犹豫模糊集。

犹豫模糊集可以表示为：

ϕ={(x,ϕ(x))|ϕ(x)∈P([0,1]),x∈X}

其中，ϕ(x)为[0,1]的一个子集，它表示X的元素x对于ϕ的隶属度的可能值。

设ϕ和ψ为X上的两个犹豫模糊集。规定：

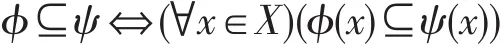
例1 设L={0,a,b,1}，其中0＜a＜b＜1，且满足运算x∧y=min{x,y}，x∨y=max{x,y}，而运算⊗、→分别如表1和表2。

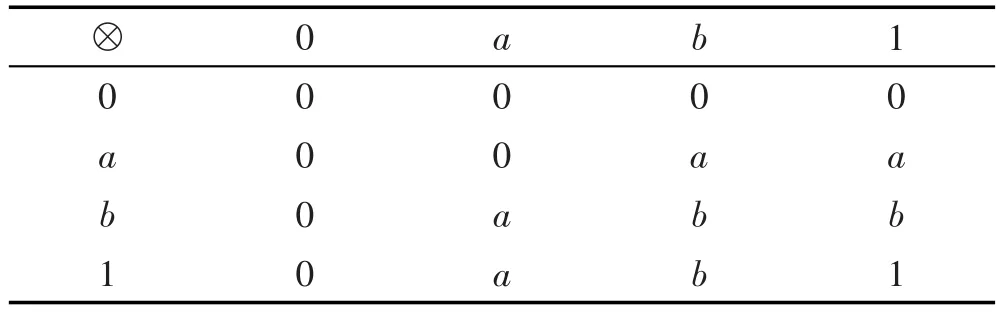
Table 1 Operation table for operation⊗表1 运算⊗表

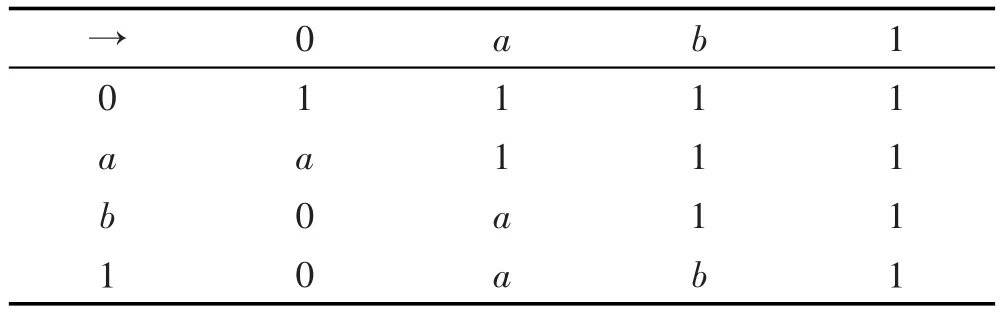
Table 2 Operation table for operation→表2 运算→表

那么L=(L,∨,∧,⊗,→,0,1)为一个剩余格。对任意x∈L，定义映射ϕ∶X→P([0,1])如下：

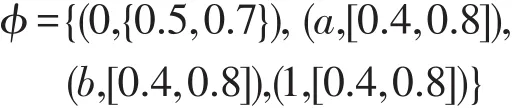
则ϕ为L上的犹豫模糊集ϕ。

文中总取剩余格L作为参考集。

3 犹豫模糊滤子

定义4设ϕ是剩余格L上的一个犹豫模糊集。称ϕ为L的犹豫模糊滤子，如果对任意x,y∈L：

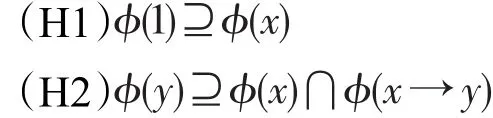
例2在例1中，容易验证ϕ为L的犹豫模糊滤子。再定义L上的犹豫模糊集ψ如下：

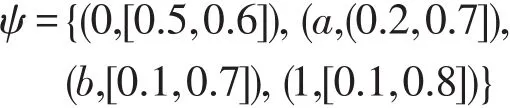
则ψ不是L的犹豫模糊滤子，因ψ(0)=[0.5,0.6]，ψ(a)⋂ψ(a→0)=ψ(a)=(0.2,0.7]⊇ψ(0)并且ψ(a)⋂ψ(a→0)≠ψ(0)。

定理1设ϕ是剩余格L上的一个犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当ϕ满足对任意x,y∈L：

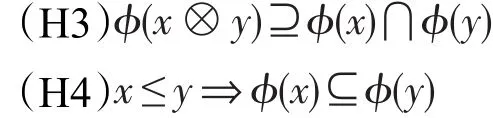
证明 设ϕ满足（H3）和（H4）。对任意x∈L，有x≤1，由（H4）知ϕ(1)⊇ϕ(x)。又x≤(x→y)→y，即x⊗(x→y)≤y，因 此ϕ(y)⊇ϕ(x⊗(x→y))⊇ϕ(x)⋂ϕ(y)。由定义4知，ϕ为L的犹豫模糊滤子。

反之，假设ϕ为L的犹豫模糊滤子。对任意x,y∈L，x→(y→(x⊗y))=1，即x≤y→(x⊗y)，因此

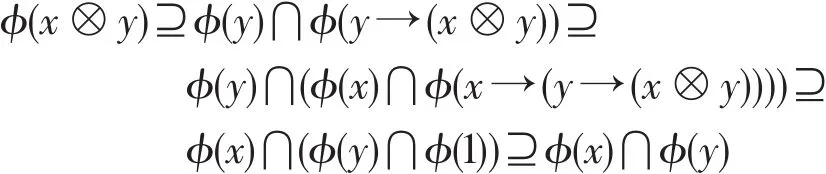
这表明ϕ满足（H3）。令x,y∈L使得x≤y，则x→y=1。因此

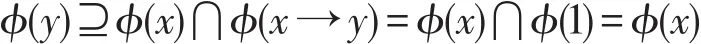
即（H4）成立。 □

定理2设ϕ是剩余格L上的一个犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当ϕ满足（H1）且对任意x,y,z∈L：

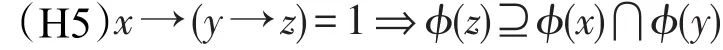
证明 假设ϕ满足（H5），取x=1，则y≤z，因此ϕ(z)⊇ϕ(y)。又x→(y→(x⊗y))=1，由（H5）知ϕ(x⊗y)⊇ϕ(x)⋂ϕ(y)，对任意x,y∈L成立，故ϕ为L的犹豫模糊滤子。

反之，设ϕ为L的犹豫模糊滤子且x→(y→z)=1对任意x,y∈L成立，则ϕ(z)⊇ϕ(y→z)⋂ϕ(y)⊇ϕ(y)⋂ϕ(x)⋂ϕ(x→(y→z))⊇ϕ(x)⋂ϕ(y)。 □

推论1设ϕ是剩余格L上的一个犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当ϕ满足（H1）且(∀x,y,z∈L)(x⊗y≤z⇒ϕ(z)⊇ϕ(x)⋂ϕ(y))。

定理3设ϕ是剩余格L上的一个犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当ϕ满足（H1）和对任意x,y,z∈L：

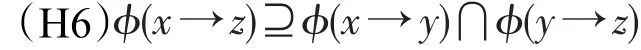
证明 假设ϕ为L的犹豫模糊滤子。因为x→y≤(y→z)→(x→z)，由（H2）可得ϕ(x→y)⊆ϕ((y→z)→(x→z))，所 以ϕ(x→z)⊇ϕ(y→z)⋂ϕ((y→z)→(x→z))，这样有ϕ(x→z)⊇ϕ(y→z)⋂ϕ(x→y)对任意x,y,z∈L成立。

反 之 ，设（H6）成 立 ，则ϕ(1→z)⊇ϕ(1→y)⋂ϕ(y→z)，即ϕ(z)⊇ϕ(y)⋂ϕ(y→z)。由定义4，ϕ为L的犹豫模糊滤子。 □

定理4设ϕ是剩余格L上的一个犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当ϕ满足对任意x,y,z∈L：

证明 假设ϕ为L的犹豫模糊滤子。对任意x，y∈L使x≤y→x，由（H4）知 ，ϕ(x)⊆ϕ(y→x)。 因ϕ((x→(y→z))→z)⊇ϕ(y→((x→(y→z))→z))∩ϕ(y)⊇ϕ(x)∩ϕ(y)。

反之，假设ϕ满足（H7）和（H8）。依（H7）有ϕ(x)⊆ϕ(x→x)=ϕ(1)。 由（H8）知 ，ϕ(y)=ϕ(1→y)=ϕ(((x→y)→(x→y))→y)⊇ϕ(x→y)⋂ϕ(x)，表明（H2）成立，故ϕ为L的犹豫模糊滤子。 □

定理5设ϕ是剩余格L的一个犹豫模糊滤子，则下列结论对任意x,y,z∈L成立：

（1）ϕ(x)⋂ϕ(y)=ϕ(x∧y)

（2）ϕ(x)⋂ϕ(y)⊆ϕ(x∨y)

（3）ϕ(x⊗z→y⊗z)⊆ϕ(x→y)

（4）ϕ(x→y)⋂ϕ(y→z)⊆ϕ(x→z)

（5）ϕ(x→(z′→y))⋂ϕ(y→z)⊆ϕ(x→(z′→z))

证明（1）对任意x,y∈L，x≤y→x，x⊗y≤x，所以x⊗y≤x∧y。 由（H4）知 ，ϕ(x⊗y)⊆ϕ(x∧y)。 因x⊗y≤x∧y≤x,y，由（HF1）和（HF2）知 ，ϕ(x)⋂ϕ(y)⊆ϕ(x⊗y)⊆ϕ(x∧y)⊆ϕ(x)⋂ϕ(y)，所以ϕ(x)⋂ϕ(y)=ϕ(x∧y)。

（2）～（5）的证明是容易的。 □

设F是L的子集，且α,β∈P([0,1])满足α⊃β。定义L上的一个犹豫模糊集ϕF(α,β)如下：

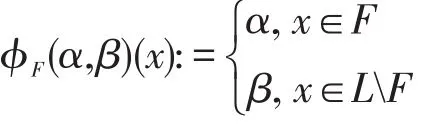
特别地，ϕF({0},{1})就是F的特征函数χF。

定理6 设F是L的非空子集，则ϕF(α,β)为L的犹豫模糊滤子当且仅当F是L的滤子。

证明 假设非空集合F是L的滤子，且x,y∈L。如果x,y∈F，则x⊗y∈F，故

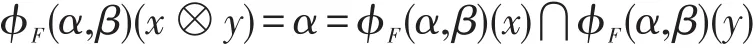
若x∉F或y∉F，则ϕF(α,β)(x)或ϕF(α,β)(y)为β，于是有ϕF(α,β)(x)⋂ϕF(α,β)(y)=β⊆ϕF(α,β)(x⊗y) ， 故（HF1）成立。进一步，令x,y∈L且x≤y。若y∈F，则ϕF(α,β)(y)=α⊇ϕF(α,β)(x)；若y∉F，则x∉F，故ϕF(α,β)(y)=β=ϕF(α,β)(x)，即（HF2）成立。综上所述，ϕF(α,β)为L的犹豫模糊滤子。

反之，设ϕF(α,β)为L的犹豫模糊滤子。对任意x,y∈L，如果x,y∈F，则ϕF(α,β)(y)=α=ϕF(α,β)(x)，于是

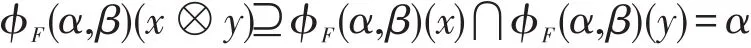
即x⊗y∈F。如果x∈F，y∈L且x≤y，则

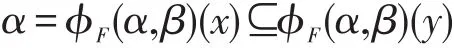
这表明y∈F。总之，F是L的滤子。 □

设ϕ为L上的犹豫模糊集，记

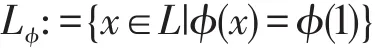
定理7如果ϕ为L的犹豫模糊滤子，则Lϕ为L的滤子。

证明 令x,y∈Lϕ，则ϕ(x)=ϕ(1)=ϕ(y)。因为ϕ为L的犹豫模糊滤子，由（HF2）及（HF3）知，ϕ(1)⊇ϕ(x⊗y)⊇ϕ(x)⋂ϕ(y)=ϕ(1)，即ϕ(x⊗y)=ϕ(1)，也就是，x⊗y∈Lϕ。令x∈Lϕ，y∈L且x≤y，则ϕ(x)=ϕ(1)。由（HF2）及（HF3）知 ，ϕ(1)⊇ϕ(y)⊇ϕ(x)=ϕ(1)，即ϕ(y)=ϕ(1)，这意味着y∈Lϕ，因此Lϕ为L的滤子。 □

设ϕ为L上的犹豫模糊集且α∈P([0,1])，记H(ϕ,α)∶={x∈L|ϕ(x)⊇α}，并称之为犹豫模糊集ϕ的α-水平子集。

定理8设ϕ为剩余格L上的犹豫模糊集，则ϕ为L的犹豫模糊滤子当且仅当对任意α∈P([0,1])，要么H(ϕ,α)=∅，要么H(ϕ,α)为L的滤子。

证明 假设ϕ为L的犹豫模糊滤子，并且α∈P([0,1])使得H(ϕ,α)≠∅。令x,y∈H(ϕ,α)，则ϕ(x)⊇α且ϕ(y)⊇α，从而

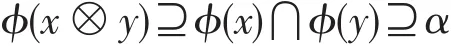
因此x⊗y∈H(ϕ,α)。现考虑x∈H(ϕ,α)，y∈L且x≤y，则ϕ(y)⊇ϕ(x)⊇α，即y∈H(ϕ,α)。综上所述，H(ϕ,α)为L的滤子。

反之，假设对任意α∈P([0,1])，H(ϕ,α)≠∅都为L的滤子。对任意x,y∈L，令ϕ(x)=α并且ϕ(y)=β，则x,y∈H(ϕ,α⋂β)，从 而x⊗y∈H(ϕ,α⋂β)，即 是ϕ(x⊗y)⊇α⋂β=ϕ(x)⋂ϕ(y)，即（HF3）成立。进一步，考虑x≤y。令ϕ(x)=α，则x∈H(ϕ,α)。因H(ϕ,α)≠∅都为L的滤子，所以y∈H(ϕ,α)，于是ϕ(y)⊇α=ϕ(x)，即（H4）成立。总之，ϕ为L的犹豫模糊滤子。 □

推论2设ϕ为剩余格L上的犹豫模糊集，且ϕ为L的犹豫模糊滤子，则对任意a∈L，当ϕ(a)≠∅时，集合{x∈L|ϕ(a)⊆ϕ(x)}为L的一个滤子。

4 犹豫模糊蕴涵滤子

定义5设ϕ是剩余格L上的一个犹豫模糊集，称ϕ为L的一个犹豫模糊蕴涵滤子，如果它满足（H1）且对任意x,y∈L，有

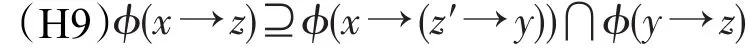
例3在例1中，定义L上的犹豫模糊集ϕ如下：，并且。容易验证，ϕ为L的犹豫模糊蕴涵滤子。若定义L上的犹豫模糊集ψ如下：且。可以验证ψ为L的犹豫模糊滤子。但不是L的犹豫模糊蕴涵滤子。事实上，取x=b,y=z=a，则。

定理9设ϕ为剩余格L的犹豫模糊滤子，则ϕ为L的犹豫模糊蕴涵滤子当且仅当

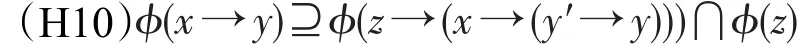
对任意x,y,z∈L都成立。

证明 假设ϕ为L的犹豫模糊蕴涵滤子，则由（H9）和（H1）知，对任意x,y,z∈L有

反之，假设ϕ为满足（H10）的犹豫模糊滤子。因x→(z′→y)=(x⊗z′)→y且(x→y)⊗(y→z)≤x→z，于是 有 (x→(z′→y))⊗(y→z)=((x⊗z')→y)⊗(y→z)≤x⊗z′→z=x→(z′→z)，所以ϕ(x→(z′→z))⊇ϕ(((x⊗z′)→y)⊗(y→z))⊇ϕ(x→(z′→y))⋂ϕ(y→z)。由假设，ϕ(x→z)⊇ϕ(1→(x→(z′→z)))⋂ϕ(1)⊇ϕ(x→(z′→z))⊇ϕ(x→(z′→y))⋂ϕ(y→z)因此ϕ为L的犹豫模糊蕴涵滤子。 □

定理10设ϕ为剩余格L的犹豫模糊滤子，则ϕ为L的犹豫模糊蕴涵滤子当且仅当

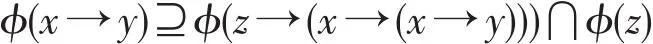
对任意x,y,z∈L都成立。

证明 类似定理9的证明。 □

定理11设ϕ为剩余格L的犹豫模糊滤子，则ϕ为L的犹豫模糊蕴涵滤子当且仅当

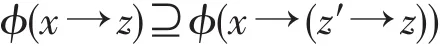
对任意x,z∈L都成立。

证明 假设ϕ为L的犹豫模糊蕴涵滤子，则

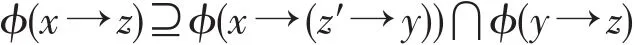
取y=z，则ϕ(x→z)⊇ϕ(x→(z′→z))⋂ϕ(1)=ϕ(x→(z′→z))。

反之，设ϕ满足ϕ(x→z)⊇ϕ(x→(z′→z))的犹豫模糊蕴涵滤子，则ϕ(x→(z′→z))⊇ϕ(y→(x→(z′→z)))⋂ϕ(y)，进而

由定理9知，ϕ为L的犹豫模糊蕴涵滤子。 □

定理12设ϕ为剩余格L的犹豫模糊滤子，则ϕ为L的犹豫模糊蕴涵滤子当且仅当

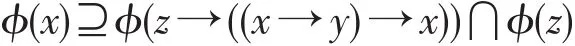
对任意x,y,z∈L都成立。

证明 类似文献[9]中定理4.12的证明。 □

类似定理8，有定理13。

定理13设ϕ为剩余格L上的犹豫模糊集，则ϕ为L的犹豫模糊蕴涵滤子当且仅当对任意α∈P([0,1])，要么H(ϕ,α)=∅，要么H(ϕ,α)为L的蕴涵滤子。

定义6设ϕ是剩余格L的一个犹豫模糊滤子，称ϕ为L的一个犹豫模糊Boolean滤子，如果对任意x∈L，有

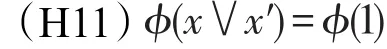
定理14设ϕ是剩余格L的一个犹豫模糊滤子，则ϕ为L的犹豫模糊Boolean滤子当且仅当ϕ为L的犹豫模糊蕴涵滤子。

证明 类似文献[26]中定理11的证明。 □

定理15在剩余格L中，每一个犹豫模糊蕴涵（Boolean）滤子ϕ都是一个犹豫模糊滤子。

证明 注意到定理12和定理14，并在定理12中取y=1便知，ϕ是一个犹豫模糊滤子。 □

定理16设ϕ是剩余格L的一个犹豫模糊滤子，则下列条件是等价的：

（1）ϕ为L的犹豫模糊Boolean滤子；

（2）(∀x∈L)(ϕ(x)=ϕ(x′→x))；

（3）(∀x,y∈L)(ϕ(x)=ϕ((x→y)→x))。

证明 类似文献[11]中定理3.8的证明。 □

定理17设ϕ和ψ是剩余格L的两个犹豫模糊滤子，使得ϕ(1)=ψ(1)且ϕ⊆ψ。若ϕ是L的犹豫模糊Boolean滤子，则ψ也是L的犹豫模糊Boolean滤子。

证明 对任意x∈L，注意到ϕ是L的犹豫模糊Boolean滤子，结合假设条件有

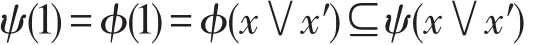
又ψ是犹豫模糊滤子，因此ψ(x∨x′)⊆ψ(1)。于是，ψ(x∨x′)=ψ(1)，再依（H11）知，ψ是L的犹豫模糊Boolean滤子。 □

类似定理8和定理13，可以得到定理18。

定理18设ϕ为剩余格L上的犹豫模糊集，则ϕ为L的犹豫模糊蕴涵（Boolean）滤子当且仅当对任意α∈P([0,1])，要么H(ϕ,α)=∅，要么H(ϕ,α)为L的蕴涵（Boolean）滤子。

5 犹豫模糊正定蕴涵（G-）滤子

定义7设ϕ是剩余格L的一个犹豫模糊滤子，称ϕ为L的一个犹豫模糊G-滤子，如果对任意x,y∈L，有

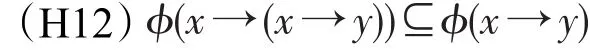
注1显然，在定义7中，条件（H12）等价于条件ϕ(x→(x→y))=ϕ(x→y)。

定义8设ϕ是剩余格L的一个犹豫模糊集，称ϕ为L的一个犹豫模糊正定蕴涵滤子，如果它满足（H1）且

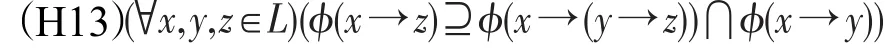
例4 设L={0,a,b,c,d,1}，L的Hasse图如图1所示。L上的算子→和⊗的定义分别如表3和表4。

那么L=(L,∨,∧,⊗,→,0,1)为一个剩余格，并且也是一个正规剩余格。现在定义L上的一个犹豫模糊集合ϕ如下：ϕ(0)={0.2,0.3}，ϕ(a)=ϕ(b)=ϕ(1)=[0.1,0.6]，ϕ(c)=[0.2,0.3]，ϕ(d)=(0.1,0.4)。可以验证，ϕ不仅是L的一个犹豫模糊正定蕴涵滤子，也是L的一个犹豫模糊G-滤子。

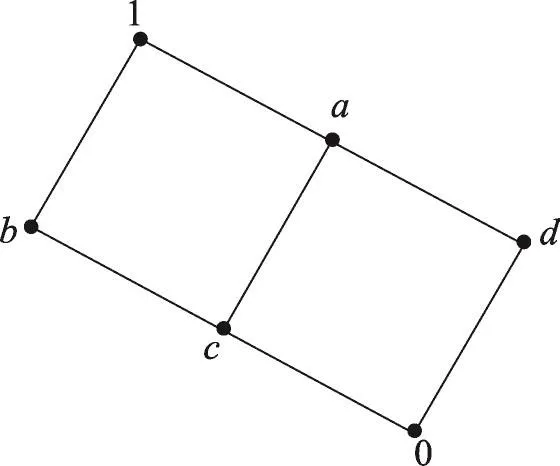
Fig.1 Hasse diagram of L图1 L的Hasse图

在（H13）中，取x=1，有定理19。

定理19在剩余格中，每个犹豫模糊正定蕴涵滤子都是犹豫模糊滤子。

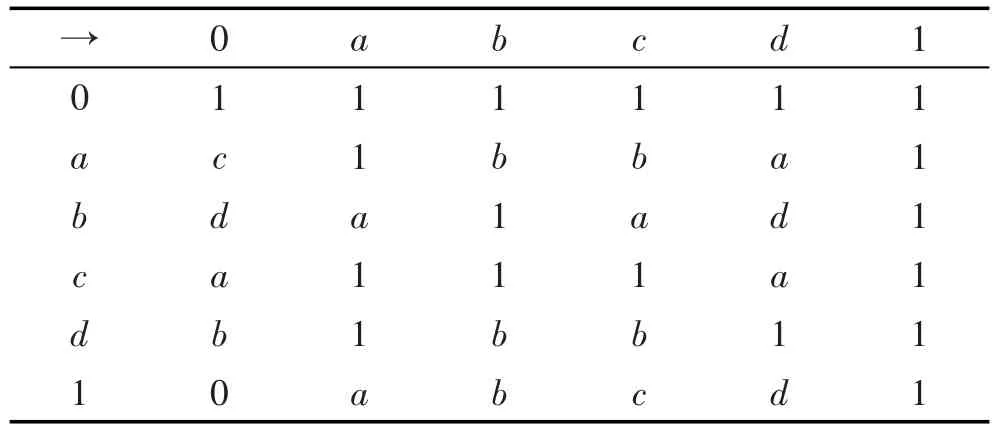
Table 3 Operation table for operatoion→表3 运算→表

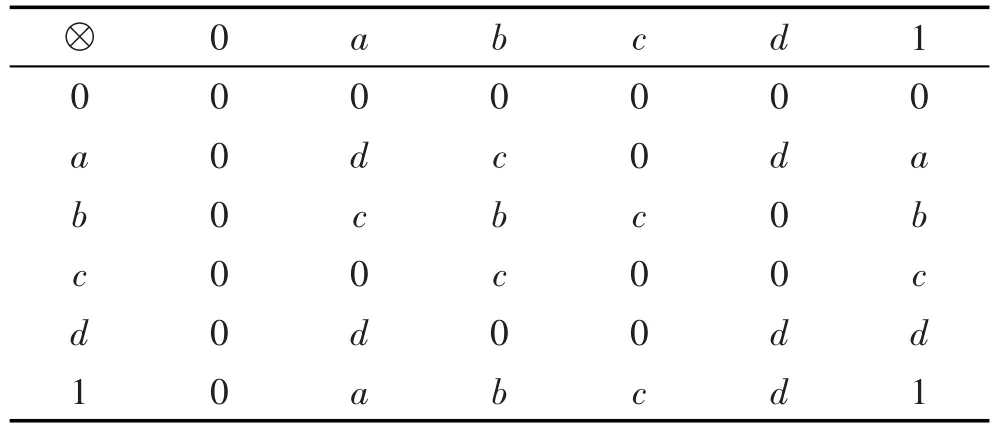
Table 4 Operation table for operation⊗表4 运算⊗表

注2定理19之逆一般不成立。在例1中，定义一个犹豫模糊集ϕ：ϕ(0)=[0.5,0.7)，ϕ(a)=ϕ(b)=(0.4,0.8]，ϕ(1)=(0.3,0.85)。容易验证，ϕ是L的犹豫模糊滤子，但它却不是L的犹豫模糊正定蕴涵滤子。事实上，ϕ(a→(a→0))⋂ϕ(a→a)=ϕ(1)⊃ϕ(a)=ϕ(a→0)，即（H12）不成立。

定理20设ϕ是剩余格L的犹豫模糊滤子，则下列结论是等价的：

（1）ϕ是犹豫模糊正定蕴涵滤子。

（2）ϕ(x→y)⊇ϕ(x→(x→y))对任意x,y∈L成立。

（3）ϕ((x→y)→(x→z))⊇ϕ(x→(y→z))对任意x,y,z∈L成立。

证明 假设ϕ是L的犹豫模糊正定蕴涵滤子，那么ϕ(x→y)⊇ϕ(x→(x→y))⋂ϕ(x→x)=ϕ(x→(x→y))⋂ϕ(1)=ϕ(x→(x→y))对任意x,y∈L成立，即（2）为真。

假设（2）为真。因ϕ是L的犹豫模糊滤子，注意到x→(y→z)≤x→((x→y)→(x→z))，有ϕ((x→y)→(x→z))=ϕ(x→((x→y)→z))⊇ϕ(x→(x→((x→y)→z)))=ϕ(x→((x→y)→(x→z)))⊇ϕ(x→(y→z))。

假设（3）成立。因ϕ是L的犹豫模糊滤子，所以ϕ(x→z)⊇ϕ(x→y)⋂ϕ((x→y)→(x→z))⊇ϕ(x→y)⋂ϕ(x→(y→z))。由定义8知，ϕ是L的犹豫模糊正定蕴涵滤子。 □

推论3设ϕ是剩余格L的犹豫模糊滤子，则ϕ是L的犹豫模糊G-滤子当且仅当ϕ是L的犹豫模糊正定蕴涵滤子。

定理21设ϕ为剩余格L的犹豫模糊滤子，则ϕ为L的犹豫模糊正定蕴涵滤子当且仅当

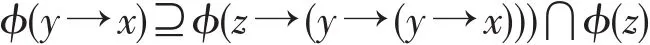
对任意x,y,z∈L都成立。

证明 假设ϕ为L的犹豫模糊正定蕴涵滤子，则ϕ(y→(y→x))⊇ϕ(z→(y→(y→x)))⋂ϕ(z)。y→x=1→(y→x)=(y→y)→(y→x)，因此ϕ(y→x)=ϕ((y→y)→(y→x))⊇ϕ(y→(y→x))⊇ϕ(z→(y→(y→x)))⋂ϕ(z)对任意x,y,z∈L都成立。

反之，因ϕ为L的犹豫模糊滤子，并且满足条件ϕ(y→x)⊇ϕ(z→(y→(y→x)))⋂ϕ(z)对任意x,y,z∈L都成 立 ，所 以ϕ(z→x)⊇ϕ((z→y)→(z→(z→x)))⋂ϕ(z→y)。 又 因z→(y→x)=y→(z→x)≤(z→y)→(z→(z→x))，故ϕ((z→y)→(z→(z→x)))⊇ϕ(z→(y→x))，进而ϕ(z→x)⊇ϕ(z→(y→x))⋂ϕ(z→y)，因此ϕ为L的一个犹豫模糊正定蕴涵滤子。 □

定理22设ϕ为剩余格L的犹豫模糊正定蕴涵滤子，则ϕ为L的一个犹豫模糊蕴涵滤子当且仅当ϕ((y→x)→x)=ϕ((x→y)→y)对任意x,y∈L成立。

证明 假设ϕ是L的一个犹豫模糊蕴涵滤子，则对 任 意x,y,z∈L，ϕ((y→x)→x)⊇ϕ(z→((((y→x)→x)→y)→((y→x)→x)))⋂ϕ(z)取z=1，那 么ϕ((y→x)→x)⊇ϕ((((y→x)→x)→y)→((y→x)→x))。因 (x→y)→y≤(y→x)→((x→y)→x)=(x→y)→((y→x)→x)≤(((y→x)→x)→y)→((y→x)→x)，注意到ϕ为L的犹豫 模 糊 滤 子 ，所 以ϕ((x→y)→y)⊆ϕ((((y→x)→x)→y)→((y→x)→x))，故ϕ((y→x)→x)⊇ϕ((x→y)→y)对任意x,y,z∈L成立。类似地，可以证明ϕ((x→y)→y)⊇ϕ((y→x)→x)对任意x,y,z∈L成立。因此对任意x,y,z∈L，ϕ((y→x)→x)=ϕ((x→y)→y)。

反之，因ϕ为犹豫模糊滤子，所以对任意x,y，z∈L，ϕ((x→y)→x)⊇ϕ(z→((x→y)→x))⋂ϕ(z)。又因(x→y)→x≤(x→y)→((x→y)→y) ，所 以ϕ((x→y)→((x→y)→y))⊇ϕ((x→y)→x)。因ϕ为犹豫模糊正定蕴涵滤子，由定理 20知，ϕ((x→y)→y)⊇ϕ((x→y)→((x→y)→y))。依假设条件ϕ((y→x)→x)=ϕ((x→y)→y)，有ϕ((y→x)→x)⊇ϕ((x→y)→x)。由y≤x→y且y→x≤z→(x→y)，因 此 (x→y)→x≤y→x≤z→(y→x)。于是，ϕ(z→(y→x))⊇ϕ((x→y)→x)，故ϕ(y→x)⊇ϕ(z→(y→x))⋂ϕ(z)⊇ϕ((x→y)→x)⋂ϕ(z)。 因 此ϕ(x)⊇ϕ((y→x)→x)⋂ϕ(y→x)⊇ϕ((x→y)→x)⋂ϕ(y→x)⊇ϕ((x→y)→x)⋂(ϕ((x→y)→x)⋂ϕ(z))⊇ϕ(z→((x→y)→x))⋂ϕ(z)⋂ϕ(z)=ϕ(z→((x→y)→x))⋂ϕ(z)，故ϕ为L的一个犹豫模糊蕴涵滤子。 □

推论4设ϕ是剩余格L的犹豫模糊蕴涵滤子，则ϕ是L的犹豫模糊蕴涵正定滤子。

定理23在剩余格中，每个犹豫模糊Boolean滤子都是一个犹豫模糊正定蕴涵滤子。

证明 设ϕ为剩余格L的犹豫模糊Boolean滤子，则ϕ(x→z)⊇ϕ((x∨x′)→(x→z))⋂ϕ(x∨x′)=ϕ((x∨x′)→(x→z))⋂ϕ(1)=ϕ((x∨x′)→(x→z))。因 (x∨x′)→(x→z)=(x→(x→z))∧(x′→(x→z))=(x→(x→z))∧((x′⊗x)→z)=x→(x→z)，所以ϕ((x∨x′)→(x→z))=ϕ(x→(x→z))。从而得到ϕ(x→(x→z))⊆ϕ(x→z)，再由定理20知，ϕ是L的犹豫模糊正定蕴涵滤子。 □

定理23的逆一般来说不成立，具体见下例。

例5 设L={0,a,b,1}满足0＜a＜b＜1，并有格运算x∧y=min{x,y}和x∨y=max{x,y}，其算子⊗和→分别定义如表5和表6。

那么L=(L,∨,∧,⊗,→,0,1)是一个剩余格。现定义一个犹豫模糊集ϕ：。容易验证，ϕ是L的犹豫模糊正定蕴涵滤子，但非犹豫模糊Boolean滤子，这是因为ϕ(a∨a′)=ϕ(a∨0)=ϕ(a)≠ϕ(1)。

定义9剩余格L的一个犹豫模糊滤子ϕ叫作L的犹豫模糊MV-滤子，如果对任意x,y∈L，有

定理24设ϕ是剩余格L上的犹豫模糊集，则ϕ是L的犹豫模糊MV-滤子的充分必要条件是：它满足（H1）且对任意x,y,z∈L，有

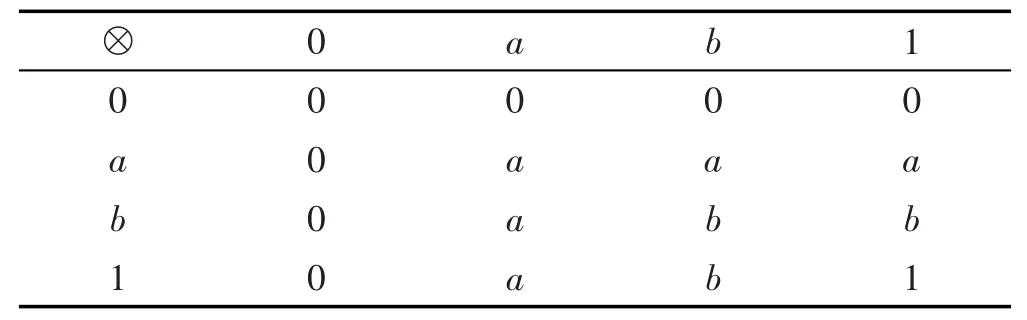
Table 5 Operation table for operation⊗表5 运算⊗表

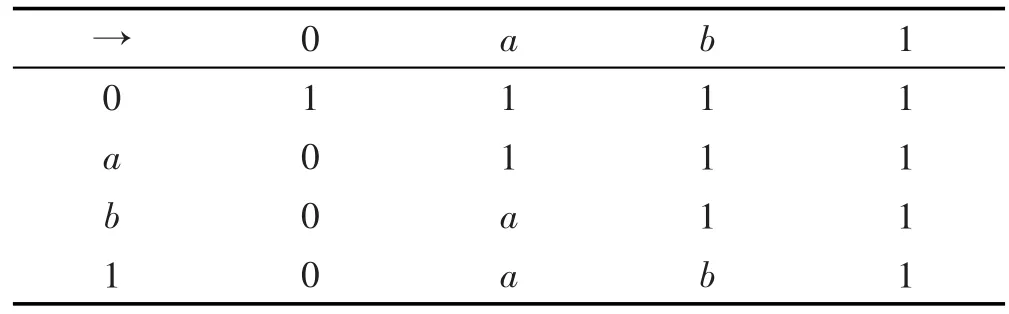
Table 6 Operation table for operation→表6 运算→表

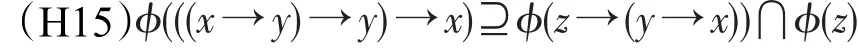
证明 类似文献[11]中定理4.24的证明。 □

在MV-代数和格蕴涵代数中，(x→y)→y=(y→x)→x且((x→y)→y)→y=x→y。于是，有推论5。

推论5在MV-代数和格蕴涵代数中，犹豫模糊滤子与犹豫模糊MV-滤子是等价的。

定理25在剩余格中，每个犹豫模糊蕴涵滤子都是一个犹豫模糊MV-滤子。

证明 假设ϕ是剩余格L的犹豫模糊蕴涵滤子。因x≤((x→y)→y)→x，所 以 (((x→y)→y)→x)→y≤x→y，进 而 ((((x→y)→y)→x)→y)→(((x→y)→y)→x)≥(x→y)→((((x→y)→y)→x)=((x→y)→y)→((x→y)→x)≥y→x，故ϕ(((((x→y)→y)→x)→y)→(((x→y)→y)→x))⊇ϕ(y→x)。因ϕ是L的犹豫模糊蕴涵滤子，故ϕ((((x→y)→y)→x))⊇ϕ(z→(((((x→y)→y)→x)→y)→(((x→y)→y)→x)))⋂ϕ(z)。取z=1，则ϕ((((x→y)→y)→x)⊇ϕ(((((x→y)→y)→x)→y)→

(((x→y)→y)→x))⊇ϕ(y→x)，因此ϕ是L的犹豫模糊MV-滤子。 □

下列例子说明定理25的逆一般不真。

例6在例1中，定义L上的犹豫模糊集ϕ如下：ϕ(0)=ϕ(a)=[0.3,0.4]，ϕ(b)=ϕ(1)=[0.2,0.6]。容易验证，ϕ是L的犹豫模糊MV-滤子，但它不是L的犹豫模糊Boolean 滤 子 ，因 为ϕ(a∨a′)=ϕ(a)=[0.3,0.4]≠[0.2,0.6]=ϕ(1)。依定义9和定理14知，ϕ不是L的犹豫模糊蕴涵滤子。

定理26剩余格L上的一个犹豫模糊集ϕ为L的一个犹豫模糊蕴涵（Boolean）滤子当且仅当ϕ既是L的一个犹豫模糊正定蕴涵滤子，也是L的一个犹豫模糊MV-滤子。

证明 假设ϕ为L的一个犹豫模糊蕴涵滤子，则依推论4和定理25知，ϕ既为L的犹豫模糊正定蕴涵滤子，同时也是L的犹豫模糊MV-滤子。

反之，假设ϕ既是L的犹豫模糊正定蕴涵滤子，也是L的犹豫模糊MV-滤子。由定理20（2）知，ϕ((x→y)→y)⊇ϕ((x→y)→((x→y)→y))又 (x→y)→x≤(x→y)→((x→y)→y)，故ϕ((x→y)→x)⊆ϕ((x→y)→((x→y)→y))，进而ϕ((x→y)→y)⊇ϕ((x→y)→x)。另一方面，因ϕ是犹豫模糊MV-滤子，所以ϕ(y→x)⊆ϕ(((x→y)→y)→x)。 又 因 (x→y)→x≤y→x对任意x,y∈L都成立，所以ϕ((x→y)→x)⊆ϕ(y→x)，故ϕ(((x→y)→y)→x)⊇ϕ((x→y)→x)，因此ϕ(x)⊇ϕ(((x→y)→y)→x)⋂ϕ((x→y)→y)⊇ϕ((x→

y)→x)⊇ϕ(z→((x→y→x))⋂ϕ(z)。故ϕ为L的一个犹豫模糊蕴涵滤子。 □

类似定理8、定理13和定理18，可以得到定理27。

定理27设ϕ为剩余格L上的犹豫模糊集，则ϕ为L的犹豫模糊正定蕴涵（MV-）滤子当且仅当对任意α∈P([0,1])，要么H(ϕ,α)=∅，要么H(ϕ,α)为L的正定蕴涵（MV-）滤子。

6 犹豫模糊正规滤子

定义10剩余格L的一个犹豫模糊滤子ϕ叫作L的一个犹豫模糊正规滤子，如果对任意x∈L，有ϕ(x″→x)=ϕ(1)。

例 7 设L=[0,1]，对任意x,y∈L，定义x∧y=min{x,y}，x∨y=max{x,y}，定义二元运算：

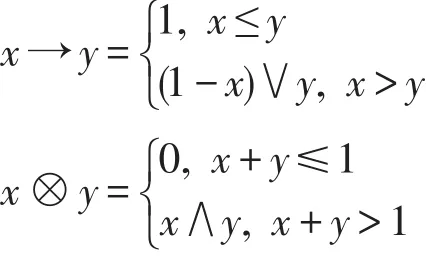
显然，L=(L,∨,∧,⊗,→0,1)是一个剩余格。定义L上的一个犹豫模糊集ϕ如下：

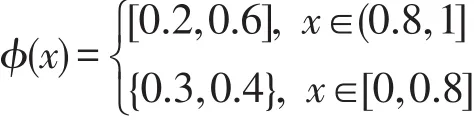
可以验证，ϕ是L的一个犹豫模糊滤子。显然，它也是L的一个犹豫模糊正规滤子。

定理28设ϕ为剩余格L的一个犹豫模糊滤子，则下列论断是等价的：

（1）ϕ为L的犹豫模糊正规滤子。

（2）(∀x,y∈L)(ϕ(y→x)⊇ϕ(x′→y′))。

（3）(∀x,y∈L)(ϕ(y′→x)⊇ϕ(x′→y))。

证明 类似文献[9]中定理5.14的证明。 □

定理29剩余格L的犹豫模糊集ϕ为L的犹豫模糊正规滤子当且仅当它满足（H1）且对任意x,y,z∈L，ϕ(y′→x)⊇ϕ(z→(x′→y))⋂ϕ(z)。

证明 类似文献[9]中定理5.17的证明。 □

定理30剩余格L的犹豫模糊集ϕ为L的犹豫模糊正规滤子当且仅当它满足（H1）且对任意x,y,z∈L，ϕ(y→x)⊇ϕ(z→(x′→y′))⋂ϕ(z)。

证明 类似文献[9]中定理3.26的证明。 □

定理31设F为剩余格L的一个R-滤子，则存在L的一个犹豫模糊正规滤子ϕ，使得某些α∈P([0,1])有H(ϕ,α)=F。

证明 定义L上的一个犹豫模糊集ϕ如下：

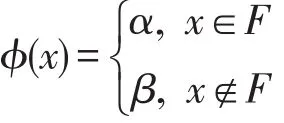
其 中α,β∈P([0,1])且α⊃β。 令x,y,z∈L使 得z→(x′→y)∈F且z∈F，则y′→z∈F，于 是ϕ(z→(x′→y))=ϕ(z)=ϕ(y′→x)=α，因 此ϕ(z→(x′→y))⋂ϕ(z)=ϕ(y′→x)。 如 果z→(x′→y)∉F或z∉F，则ϕ(z→(x′→y))=β或ϕ(z)=β，因此ϕ(z→(x′→y))⋂ϕ(z)=β⊆ϕ(y′→x)。 故 对 任 意x,y,z∈L，总 有ϕ(z→(x′→y))⋂ϕ(z)⊆ϕ(y′→x)。

另一方面，因1∈F，所以ϕ(1)=α⊇ϕ(x)对任意x∈L成立。总之，ϕ是L的一个犹豫模糊正规滤子，并且对于α∈P([0,1])有H(ϕ,α)=F。 □

类似定理8、定理13、定理18和定理17，有定理32。

定理32设ϕ为剩余格L上的犹豫模糊集，则ϕ为L的犹豫模糊正规滤子当且仅当对任意α∈P([0,1])，要么H(ϕ,α)=∅，要么H(ϕ,α)为L的R-滤子。

定理33设ϕ为剩余格L上的犹豫模糊集。如果ϕ为L的犹豫模糊MV-滤子，则ϕ为L的犹豫模糊正规滤子。

证明 因ϕ为犹豫模糊MV-滤子，所以对任意x,y∈L，ϕ(((x→y)→y)→x)⊇ϕ(y→x)。故ϕ(x″→x)=ϕ(((x→0)→0)→x)⊇ϕ(0→x)=ϕ(1)。依（H1）有ϕ(x″→x)=ϕ(1)，所以ϕ为L的犹豫模糊正规滤子。 □

定理32的逆一般不真，见下例。

例8在例7中，ϕ为L的一个犹豫模糊正规滤子，但它不是L的一个犹豫模糊MV-滤子。事实上，ϕ(((0.8→0.3)→0.3)→0.8)=ϕ(0.8)={0.3,0.4}⊂[0.2,0.6]=ϕ(0.3→0.8)。

定理34在BL-代数L中，L的犹豫模糊MV-滤子与L的犹豫模糊正规滤子是等价的。

证明 类似文献[9]中定理7.6的证明。 □

定理35设ϕ是剩余格L的一个犹豫模糊集，ϕ是L的犹豫模糊Boolean滤子当且仅当ϕ既是L的犹豫模糊正规滤子，又是L的犹豫模糊正定蕴涵滤子。

证明 假设ϕ是L的犹豫模糊Boolean滤子，由定理26和定理33知，ϕ既是L的犹豫模糊正规滤子，又是L的犹豫模糊正定蕴涵滤子。

反之，假设ϕ既是L的犹豫模糊正规滤子，又是L的犹豫模糊正定蕴涵滤子。对任意x,y∈L，因x′≤x→y，所 以 (x→y)→x≤x′→x，因 此ϕ((x→y)→x)⊆ϕ(x′→x)。 由x′→x=(x″)′→x知 ，ϕ(x′→x)⊆ϕ(x′→x″)。又因x′→x″=x′→(x′→ 0)，由注1有，ϕ(x′→x″)=ϕ(x′→(x′→0))=ϕ(x′→0)=ϕ(x″)=ϕ(x)。可得ϕ((x→y)→x)⊆ϕ(x′→x)=ϕ(x)，进 一 步 ，ϕ((x→y)→x)=ϕ(x)。依定理16知，ϕ为L的犹豫模糊Boolean滤子。 □

推论6在格蕴涵代数中，犹豫模糊G-滤子和犹豫模糊Boolean滤子是等价的。

在正规剩余格L中，x″=x对于任意x∈L都成立，因此下列推论是明显的。

推论7在正规剩余格中，犹豫模糊G-滤子和犹豫模糊Boolean滤子是等价的。

定理36设ϕ和ψ是剩余格L的两个犹豫模糊滤子，使得ϕ(1)=ψ(1)且ϕ⊆ψ。若ϕ是L的犹豫模糊正规滤子，则ψ也是L的犹豫模糊正规滤子。

证明 对任意x∈L，注意到ϕ是L的犹豫模糊正规滤子，结合假设条 件 有ψ(1)=ϕ(1)=ϕ(x″→x)⊆ψ(x″→x)。 又ψ是L的犹豫 模 糊滤子，故ψ(x″→x)⊆ψ(1)。于是，ψ(x″→x)=ψ(1)对任意x∈L成立。再依定义10知，ψ是L的犹豫模糊正规滤子。 □

7 结论

人工智能的重要任务之一就是使计算机模拟人脑去处理不确定性问题。非经典逻辑为该任务奠定了技术基石，这些非经典逻辑的代数语义对应着不同的逻辑代数类。剩余格是一类较广的逻辑代数，而滤子理论是研究代数结构的重要工具，因此针对剩余格的滤子理论反作用于推理系统进行研究，进而构成机器识别、判断、推理等智能性活动的基础。本文把犹豫模糊集应用于剩余格的滤子研究中，初步建立剩余格的犹豫模糊滤子理论。主要引入了剩余格的犹豫模糊（蕴涵、Boolean、正定蕴涵、MV、正规）滤子等概念，给出这些犹豫模糊滤子系列新特征，建立起它们的若干关系。人类决策常常表现出犹豫的现象，在确定元素的隶属度时会在几个值之间犹豫。模糊集及其一些扩展理论无法反映这样思维过程。因此，犹豫模糊滤子理论不同于已有模糊滤子理论，以此建立起的智能机更贴近人类思维活动真相。该理论方法可以用于MV-代数、格蕴涵代数、BL-代数、MTL-代数等讨论中。

[1]Ward M,Dilworth R P.Residuated lattices[J].Transactions of theAmerican Mathematical Society,1939,45:335-354.

[2]Hájek P.Metamathematics of fuzzy logic[M].Springer Netherlands,1998.

[3]Xu Yang.Lattice implication algebras[J].Journal of Southwest Jiaotong University,1993,28(1):20-27.

[4]Turunen E.BL-algebras of basic fuzzy logic[J].Mathware and Soft Computing,1999,6(1):49-61.

[5]Chang C C.Algebraic analysis of many valued logic[J].Transactions of the American Mathematical Society,1958,88(2):467-490.

[6]Esteva F,Godo L.Monoidal t-norm based logic:towards a logic for left-continuous t-norms[J].Fuzzy Sets and Systems,2001,124:271-288.

[7]Wang Guojun.MV-algebras,BL-algebras,R0-algebras and multiple-valued logic[J].Fuzzy Systems and Mathematics,2002,16(2):1-15.

[8]Turunen E.Boolean deductive systems of BL-algebras[J].Archive for Mathematical Logic,2001,40(6):467-473.

[9]Zhu Yiquan,Xu Yang.On filter theory of residuated lattices[J].Information Sciences,2010,180(19):3614-3632.

[10]Liu Yi,Qin Xiaoyan,Xu Yang.Interval-valued intuitionistic(T,S)-fuzzy filters theory on residuated lattices[J].International Journal of Machine Learning and Cybernetics,2014,5(5):683-696.

[11]Liu Yi,Xu Yang,Qin Xiaoyan.Interval-valued T-fuzzy filters and interval-valued T-fuzzy congruences on residuated lattices[J].Journal of Intelligent and Fuzzy Systems,2014,26(4):2021-2033.

[12]Wang Zhudeng,Fang Jinxuan.On V-filters and normal V-filters of a residuated lattice with a weak VT-operator[J].Information Sciences,2008,178(17):3465-3473.

[13]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[14]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[15]Zadeh L A.The concept of a linguistic variable and its application to approximating reasoning-I[J].Information Sciences,1975,8:119-249.

[16]Dubois D.Fuzzy sets and systems:theory and applications[M].Orlando,USA:Academic Press,Inc,1980.

[17]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.

[18]Rodriguez R M,Martinez L,Herrera F.Hesitant fuzzy linguistic term sets for decision making[J].IEEE Transactions on Fuzzy Systems,2012,20(1):109-119.

[19]Wei Guiwu.Hesitant fuzzy prioritized operators and their application to multiple attribute decision making[J].Knowledge-Based Systems,2012,31(7):176-182.

[20]Xia Meimei,Xu Zeshui.Hesitant fuzzy information aggregation in decision making[J].International Journal of Approximate Reasoning,2011,52(3):395-407.

[21]Xu Zeshui,Xia Meimei.Distance and similarity measures for hesitant fuzzy sets[J].Information Sciences,2011,181(11):2128-2138.

[22]Zhu Bin,Xu Zeshui,Xia Meimei.Hesitant fuzzy geometric Bon-Ferroni means[J].Information Sciences,2012,205(1):72-85.

[23]Rezaei A,Saeid A B.Hesitant fuzzy filters in BE-algebras[J].International Journal of Computational Intelligence Systems,2016,9(1):110-119.

[24]Yun Y B,Song S Z.Hesitant fuzzy prefilters and filters of EQ-algebras[J].Applied Mathematical Sciences,2015,9(11):515-532.

[25]Yun Y B,Song S Z.Hesitant fuzzyset theory applied to filters in MTL-algebras[J].Honam Mathematical Journal,2014,36(4):813-830.

[26]Liu Lianzhen,Li Kaitai.Fuzzy implicative and Boolean filters ofR0-algebras[J].Information Sciences,Information Sciences,2005,171(1/3):61-71.

附中文参考文献：

[3]徐杨.格蕴涵代数[J].西南交通大学学报,1993,28(1):20-27.

[7]王国俊.MV-代数、BL-代数,R0-代数与多值逻辑[J].模糊系统与数学,2002,16(2):1-15.

2016-08,Accepted 2016-12.

Hesitant Fuzzy Filter Theory of Residuated Lattices*

PENG Jiayin+
College of Mathematics and Information Sciences,Neijiang Normal University,Neijiang,Sichuan 641199,China
+Corresponding author:E-mail:pengjiayin62226@163.com

By applying hesitant fuzzy set to the filter theory of residuated lattices,this paper proposes the concepts of hesitant fuzzy filters,hesitant fuzzy implicative filters,hesitant fuzzy positive implicative filter,hesitant fuzzy MV-filters and hesitant fuzzy regular filters of residuated lattices,investigates their properties,discusses their relations,and obtains some equivalent characterizations between them.Then,this paper gives the conditions for a hesitant fuzzy set translating into a hesitant fuzzy filter and for a hesitant fuzzy filter translating into a hesitant fuzzy(positive implicative,MV,regular)implicative filter.Finally,this paper studies the relations between kinds of filters and its corresponding level filters,and establishes the extension theorems of hesitant fuzzy Boolean filters and hesitant fuzzy regular filters of residuated lattices.

residuated lattice;hesitant fuzzy set;hesitant fuzzy(implicative,positive implicative,MV,regular)filter;level sets of a hesitant fuzzy set

10.3778/j.issn.1673-9418.1608028

*The National Natural Science Foundation of China under Grant No.11071178(国家自然科学基金);the Comprehensive Reform of Mathematics andApplied Mathematics of the Ministry of Education of China under Grant No.ZG0464(教育部数学与应用数学专业综合改革).

CNKI网络优先出版:2016-12-07,http://www.cnki.net/kcms/detail/11.5602.TP.20161207.0922.002.html

PENG Jiayin.Hesitant fuzzy filter theory of residuated lattices.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1860-1870.

A

TP18；O141；O153

PENG Jiayin was born in 1962.He is a Ph.D.candidate at Sichuan Normal University and a professor at Neijiang Normal University.His research interests include fuzzy mathematics and artificial intelligence,etc.

彭家寅（1962—），男，四川资中人，四川师范大学博士，内江师范学院教授，主要研究领域为模糊数学，人工智能等。发表学术论文100多篇，主持省部级基金项目多项。