一种对流层散射超视距定位模型的误差分析*

徐建敏, 夏飞海, 张冰龙

(中国电子科技集团公司第36研究所, 浙江嘉兴 314033)

一种对流层散射超视距定位模型的误差分析*

徐建敏, 夏飞海, 张冰龙

(中国电子科技集团公司第36研究所, 浙江嘉兴 314033)

针对超视距目标辐射信号容易受到对流层散射和地球曲率的影响而难以定位的情况,文中对基于双站交叉定位的超视距无源定位模型进行了研究。通过分析超视距目标信号在对流层散射传播的特点,推导了基于对流层散射传播的球面交叉定位计算模型,并且给出了球面交叉定位和传统平面交叉定位的误差分析。仿真结果表明,在上百千米级别的超视距定位中,球面交叉定位与传统平面交叉定位的定位偏差基本可以忽略。

无源交叉定位;超视距;对流层散射;定位偏差

0 引言

无源定位技术由于其作用距离远、隐蔽性好等优点而深受军方青睐,在对目标定位时,常用两个测向站的测向线交叉定位方式来获得辐射源信号的位置[1-2]。

传统的测向交叉定位技术是将辐射源和测向站放在一个平面上进行定位的,并且假定电波信号直线传播。这种交叉定位方式将大气散射和地球曲率的影响忽略不计,适用于视距内目标信号的侦察。然而,对超视距目标进行侦察时,这种交叉定位方式就不适用了,由于电波在超视距传播时会受到大气层的散射作用,电波信号的传播轨迹将发生变化,如图1所示,电波的传播轨迹可能是TB+BR,也可能是TA+AR或其他方式。由于目标和测向站的距离很远,两者应该等效在同一个曲面上,而不是一个平面上,

因此,如果采用传统测向交叉定位方式对超视距目标进行定位,将会引起很大误差[3-5]。

由于这些原因,文中对基于双站交叉定位的超视距无源定位模型进行研究,求解受地球曲率影响,非直线传播的定位计算模型,并仿真了传统平面交叉定位与球面交叉定位的定位误差差异。此处均假设单站只对目标方位角进行测向,因此,双站交叉定位对目标高度不敏感,以下测向定位模型的推导和仿真均认为目标位于地球表面上。

1 定位模型

由图1可知,当对超视距目标进行交叉定位时,由于电波信号受到大气层的散射影响,电波信号传播轨迹将发生改变,这给对目标进行定位带来了很大困难。由于辐射源信号沿路径TDR传播到测向站的距离最短,其能量损失最小,因此可认为散射体位于测向站、辐射源和球心所决定的平面内,即可先将电波轨迹投影到地球表面,然后在地球表面进行球面定位。

1.1 传统平面交叉定位

基于通信侦察的双站平面交叉定位技术成熟。如图2所示,两测向站DF1、DF2的坐标位置为(x1,y1)、(x2,y2)。两测向站经过对目标测向后得到的目标方位角分别为φ1、φ2,则两目标方位角的交叉线所在位置即为目标位置,其坐标记为(xT,yT)。

通过计算可得下式:

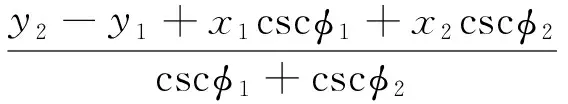
(1)

(2)

假设两测向站DF1、DF2的自身定位误差忽略不计,只考虑测向站的测向误差,并且两测向站的测向误差的最大值均为±Δθ。则由两测向站形成的±Δθ宽度的扇形交叉形成的四边形区域即为目标真实位置所在区域,这个区域称为双站交叉定位的定位模糊区,定位模糊区越小,定位精度越高。

如果将2个测向站与目标放入一个平面内对超视距目标进行定位处理,就会引入由地球曲率和对流层散射影响造成的定位误差,下面将侧重分析考虑由地球曲率和对流层散射影响的球面交叉定位原理。

1.2 球面交叉定位

在球面上,测向线以弧线的方式表示,如图3所示。其理论推导如下:

以A点为测向站点,B点代表目标,AC、BC弧线为A、B两点的正北方向。则形成的弧线AB代表B点相对A点的测向线。

A、B、C三点形成弧面三角形,∠A、∠B、∠C分别代表三角形的夹角,即∠A为面OAC与面OAB的夹角、∠B为面OBC与面OAB的夹角、∠C为面OAC与面OBC的夹角。所以,B点相对A点的球面测向角度为∠A;∠a、∠b、∠c分别为各点与地心的夹角。

假设A点的经纬度为(Aj,Aw),B点的经纬度为(Bj,Bw)。则根据三面角余弦公式,可得:

cos(c)=sin(Bw)sin(Aw)+

cos(Bw)cos(Aw)cos(Bj-Aj)

(3)

由此可得:

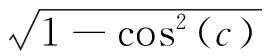
(4)

由球面正弦公式可得:

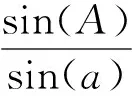
(5)

由于C=Bj-Aj,c=90°-Bw,可得:

(6)

即目标点的测向结果可以用A、B两点的经纬度表示。

由上述角度公式可得,如果A1、A2两点为超视距测向站,B点为目标位置,只要能按照球面交叉的方式,即可得到目标位置,如图4所示。

在这里假设A1、A2、B三点的经纬度分别为(A1j,A1w)、(A2j,A2w)、(Bj,Bw),则由上面的分析可得A1、A2测向站的球面测向角度为:

(7)

(8)

式中c1、c2分别表示两测向站与目标到地心的夹角。通过上述两个测向公式,可以得到目标B的球面交叉位置。

2 球面交叉和平面直角交叉的误差分析

此处分析不同坐标系下定位误差的偏差时,不考虑测向站自定位误差和自身的测向误差,而仅考虑不同坐标系造成的定位偏差。如果按照平面直角坐标系进行解算,首先需要把经纬度映射到平面直角坐标系,坐标系的选择一般如图5和图6所示。

在计算出目标位置的结果后T点也按照同样的方式反映射到球面目标B,所以如果按照一致的映射原则,基准点A1的测向在两个坐标系下都不会对定位结果造成影响。

那么A2点转化为平面直角坐标系下的点为:

Xa2=Rcos(A2w)cos(A2j)

Ya2=Rcos(A2w)sin(A2j)

(9)

同样B点也可以如此转化,由于B点在A1点正上方,转化为直角坐标系时映射到Y轴上,即Xb=0。因此,B点相对A2点的平面测向角度为:

(10)

该测向角度和式(8)是否存在差异,可以通过仿真数据比较。分别假定两测向站基线为100 km、200 km和300 km,A1测向站位于北极点,经纬度假设为(0°,90° N),A2测向站经纬度分别为(0°,89° N)、(0°,88° N)和(0°,87° N)。改变目标B与测向站A1的距离,即目标B从A1北极点移到北纬84°位置(经度为90°不变),变化距离从0 km到660 km。画出测向站A2对目标B在两个坐标系下的测向差曲线(如图7所示),同时画出两个测向站在平面和球面两个坐标系下的交叉定偏差曲线(如图8所示)。

可以看出,在将球面上的测向站和目标都映射到平面直角坐标系上进行测向和定位处理时,测向站A2的测向值在球面测向角度的基础上增加了一个误差量,导致定位结果的偏差。从图7可以看出,当目标B从A1北极点移到北纬84°位置(即目标B从A1点移到距A1北极点660 km左右的位置),两个坐标系下的测向差会逐渐增大,A2测向站与A1测向站基线越大,两个坐标系下的测向差就越大,在300 km基线时的两坐标系测向差约为0.13°。

同理,从图8可以看出,平面交叉定位和球面交叉定位的定位结果偏差量相对较小,在最大300 km基线时,定位结果偏差在1.5 km以内(目标距测向站660 km时),相对误差仅为0.23%。

3 结论

文中介绍了双站交叉定位的超视距无源定位模型,求解了在地球曲率影响下非直线传播的球面交叉定位计算模型,并仿真了不同基线长度下,传统平面

交叉定位与球面交叉定位的定位误差差异。仿真结果显示,基线变长,定位结果偏差变大,在300 km基线下,对660 km远目标进行基于对流程散射的双站交叉定位效能评估中,完全可利用平面交叉定位模型代替球面交叉定位模型进行仿真评估,两者的偏差值不到1.5 km,相对误差仅为0.23%。

由于平面交叉定位算法在通信侦察领域已广泛应用,在视距乃至上百千米级别的超视距交叉定位中可统一利用平面交叉定位方法进行快速定位,直观地给出定位效能。

[1] 贺刚, 赵雷鸣, 刘昊, 等. 双机协同交叉定位算法及误差分析 [J]. 火力与指挥控制, 2015, 40(11): 69-71.

[2] 沈晓峰, 徐保根, 邹继锋, 等. 基于正性约束的测向交叉定位方法 [J]. 电子科技大学学报, 2014, 43(6): 834-837.

[3] 胡来招. 无源定位 [M]. 北京: 国防工业出版社, 2004: 65-68.

[4] 张利军, 张蕊, 赵振维. 对流层散射传播中的偏移损耗分析 [J]. 电子与信息学报, 2015, 37(6): 1502-1506.

[5] HE Qing, LUO Laiguan. Analysis of over-the-horizon target detection based on the small aperture array [C]∥7th International Congress onImage and Signal Processing (CISP). New York: IEEE, 2014: 1100-1104.

欢迎订阅《弹箭与制导学报》

《弹箭与制导学报》是由中国科学技术协会主管、中国兵工学会主办、中国兵器工业第203研究所承办的学术性刊物。本刊的宗旨是报道导弹、火箭、弹药、弹道及制导兵器技术相关专业的学术性论文，突出报导高新技术在本专业领域方面的理论研究成果，反映科研、生产、使用、教学上的最新应用成果，为我国国防现代化建设服务。

本刊为中文核心期刊。被美国《剑桥科学文摘：工程技术》(CSA)、美国《乌利希期刊指南》(UPD)、英国《物理学、电技术、计算机及控制信息社数据库》(INSPEC)、 日本《日本科学技术振兴机构数据库》(JST)收录。是《中国科技论文统计与分析》、《中国学术期刊文摘》、《中国科学引文数据库》、《中国学术期刊综合评价数据库》源刊；已入网“万方数据——数字化期刊群” 、“中国知网”即《中国学术期刊(光盘版)》以及《中文科技期刊数据库》(维普)。本刊国内外公开发行。

《弹箭与制导学报》为双月刊，大16开，彩色印刷，定价：每期50.00元、全年300.00元。

邮局汇款：西安市丈八东路10号学报编辑部邮编：710065

收款人：弹箭与制导学报学报编辑部

银行汇款：户名：西安现代控制技术研究所

开户银行：中国工商银行西安南大街支行账号：3700 0201 0900 3706 536

联系人：何晓东电话：02988293167传真：02988293333

通信地址：西安市丈八东路10号学报编辑部E-mail：djzdxb@163.com邮编：710065

AnerrorAnalysisofLocationModelofOver-the-horizonBasedonTroposcatter

XU Jianmin, XIA Feihai, ZHANG Binglong

(No.36 Research Institute of CETC, Zhejiang Jiaxing 314033, China)

Aiming at the condition that the over-the-horizon target is difficult to locate under the influence of tropospheric scattering and the earth’s curvature, passive location model of OTH based on double stations cross location is researched in this paper. A calculation model of spherical cross location based on troposcatter is deduced by analyzing the characteristics of the propagation of the OTH target signal in the troposphere. Finally, the error analysis was given between spherical cross location and traditional plane cross location. The simulation result shows that the localization error of spherical cross location and traditional plane cross location can be ignored basically in the level of hundreds of kilometers for OTH target location.

passive cross location; over-the-horizon (OTH); troposcatter; localization error

TN926

A

2016-06-22

徐建敏(1982-),男,浙江台州人,高级工程师,硕士,研究方向:超视距信号处理。