PPP中接收机钟差和卫星钟差对动态对流层延迟解算的影响*
2014-09-20徐韶光熊永良
徐韶光 熊永良 李 鹏
(西南交通大学地学学院测绘系,成都 611756)
PPP中接收机钟差和卫星钟差对动态对流层延迟解算的影响*
徐韶光 熊永良 李 鹏
(西南交通大学地学学院测绘系,成都 611756)
实验发现,当接收机发生钟跳时,对流层参数解算精度会受到严重影响。在对流层参数估计时,若固定测站坐标,则接收机钟差和对流层延迟参数相关性大大增强,对流层延迟的估计精度会随着接收机钟差精度的降低而降低,反之亦然。采用2012-07-21北京市区和房山区两个台站的数据分析表明,利用精密单点定位技术和IGS预报产品实时反演的水汽精度为2~3 mm。
精密单点定位;接收机钟差;卫星钟差;对流层延迟;反演
Bevis等[1-3]利用GPS反演出精度较高的可降水量。为消除各种误差源,常采用差分GPS技术获取对流层延迟,但在数据处理过程中对流层天顶延迟与高程方向强相关,随着测站间高差的增大,对流层解算的精度也随之降低[4];此外,在短基线网络中,各站点间对流层强相关,难以分离。为克服上述问题,不少学者引入非差模式估计对流层[5-6],该模式求解对流层需进行各项误差源改正并引入接收机钟差参数,而钟跳的发生可能会导致错误的解算结果。接收机钟差与其余待估参数间存在相关性,固定测站坐标时对流层参数的精度能否提高有待研究。对于实时对流层延迟的获取则需考虑实时卫星钟差的质量[7],而实时卫星钟差的特性及实时对流层延迟的精度能否满足气象预报的要求也需要进一步分析。
1 对流层延迟估计原理
精密单点定位的计算模型为:
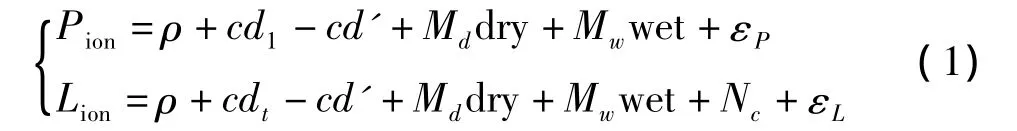
概略干延迟通过GPT模型求取[8],卫星钟差采用IGS提供的产品,则待估参数为:
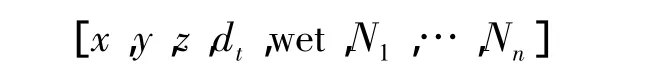
其中x、y、z为测站坐标,Nn为第n颗卫星对应的组合模糊度。若固定测站坐标,则无需估计x、y、z。
当接收机发生钟跳时,Kalman滤波过程中原有的更新结果可能会遭到破坏[9]。固定测站坐标虽然减少了待估参数个数,但会增加对流层与接收机钟差的相关性。此外,实时卫星钟差的特性也会对滤波过程产生影响。
2 接收机钟性能对天顶对流层延迟的影响
2.1 钟跳对对流层延迟的影响和解决方法
选取有代表性的测站,估计得到测站接收机2008-10-10的钟差结果(图1)。图中ALGO站安置外置原子钟,其余站安装石英钟,图中的钟差按等效距离误差标注。由图1知,ALGO站的接收机钟差较规律,呈线性变化,AIRA站和SHAO站虽然变化没有规律,但历元间接收机钟差变化较缓慢,而URUM站与MIZU站每隔一段时间跳变一次,URUM站跳变量约为1 ms,MIZU站高达约20 ms。URUM站在伪距和相位上同时发生钟跳,称为第1类钟跳;MIZU站仅在伪距上发生钟跳,称为第2类钟跳;若仅在相位上发生钟跳,称为第3类钟跳。
利用PPP估计所得的对流层延迟与CODE分析中心提供的最终对流层进行比较(图2)。CODE提供的对流层延迟是BERNESE网解得到的结果(每2 h估计一次),本文的参数均采用逐历元解算。由于CODE没有提供AIRA站的对流层延迟,所以这里以NRC机构的CRSC-PPP解算的对流层延迟为参考。CODE提供的延迟值以圆圈表示。

图1 各测站的接收机钟差Fig.1 Receiver clock errors of all stations
由图2知,对于没有发生钟跳的测站,利用最终IGS产品解算对流层的精度较好,收敛后与CODE提供的事后产品相差1~2 cm,相应的可降水量精度为1.5~3 mm。在最后的15 min内,对流层都有发生骤变的现象,产生此现象的原因是卫星的轨道外推精度降低造成的。而对于发生钟跳的MIZU站与URUM站,前者的对流层每隔一段时间会发生mm级至cm级的跳变,导致对流层解算过程中每隔一段时间需重新初始化,尽管收敛的时间较快,但不利于对流层延迟参数的连续解算。测试表明,第1类钟跳对对流层估计没有影响,因为该类钟跳引起的跳变能完全被接收机钟差吸收,所以URUM站的对流层连续性没有遭到破坏;第2类钟跳严重影响对流层参数计算的结果,其原因是突变的接收机钟差被位置参数、对流层参数和模糊度参数各吸收一部分,且对对流层延迟参数解算的影响较大。
由Kalman滤波过程分析造成上述结果的原因。其模型为:
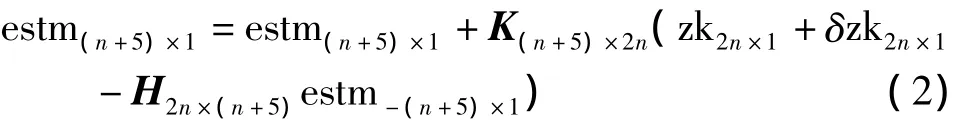
式中,H为对应相位和伪距观测量的设计矩阵,zk为未发生钟跳的观测量,δzk为实际钟跳大小,K为增益矩阵。estm为未知参数更新值,estm为未知参数预测值。
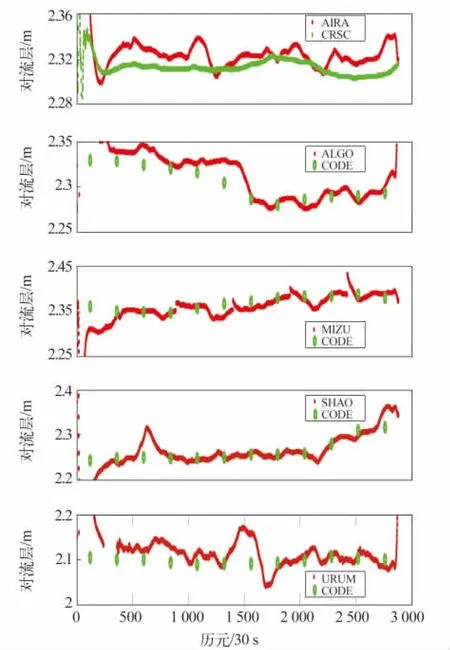
图2 CODE和本文计算的对流层延迟Fig.2 ZTD from CODE and from author’s experiment
若在伪距观测值上发生钟跳,更新过程为:
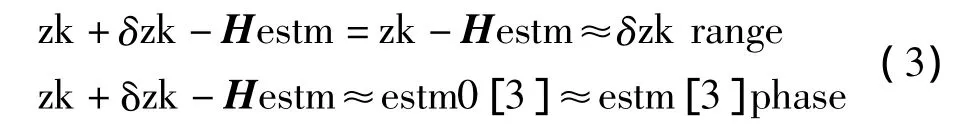
式中,estm0为未发生钟跳的参数值。由式(3)可知,仅在伪距观测量发生钟跳,将会导致方程中的接收机钟差基准不一致;若伪距和相位同时发生相等的跳变,则观测方程中的接收机钟差基准仍保持一致而不会引起解算参数的跳变。
为解决以上问题,笔者采用改进的初始化部分参数的处理策略,其流程如图3所示,其中伪距阈值可以设置为50 000 m,相位则可以设置对应的周数,相位补偿可采用Clockprep软件[10]。若进行实时数据处理,则采用删除观测量的方法。
对MIZU站进行处理并重新估计对流层参数的结果见图4。从图4可以看出,MIZU站的对流层延迟跳变消失,得到较为平滑的结果,在不同的跳变时刻,相应的解算精度分别提高约 1、2、2、2、5 cm,而收敛到正常精度需要15~30 min,对整体精度而言可提升2 mm。由此可见,该方法可以有效消除接收机钟跳对解算结果的影响,并提高对流层延迟参数解算的精度。
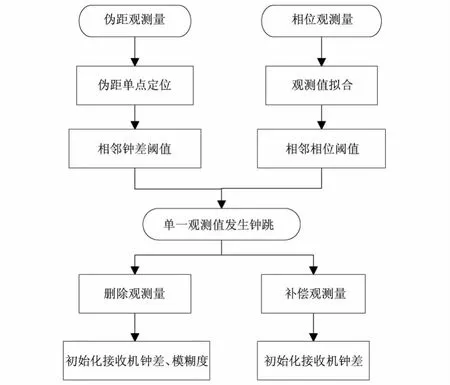
图3 钟跳处理流程Fig.3 Flow chat of clock jump processing
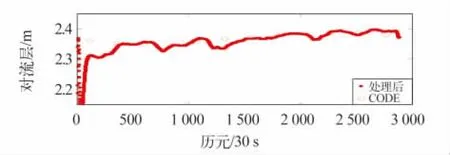
图4 钟跳处理后的对流层延迟Fig.4 ZTD after correction of clock jump
2.2 固定测站坐标对对流层延迟参数解算的影响
对于静止台站,相邻单天间的坐标差很小,故第2天的测站坐标可以采用第1天的计算结果,通过固定测站坐标以减少待估参数的个数。但对于非差模式,固定测站坐标后,由于坐标作为已知值与其余参数没有相关性,导致其余参数之间的协方差绝对值增大,而方差变化较小。由式(4)可知,接收机钟差和对流层之间的相关性将大大增强:

固定测站坐标后得到的对流层延迟结果如图5所示,其中fix表示固定测站坐标后的结果,fixR表示固定测站坐标后的接收机钟差和对流层之间的相关系数,relR表示未固定测站坐标时两者的相关系数。以CODE结果为参照值,计算结果表明,AIRA站和ALGO站的对流层延迟参数计算的平均精度与未固定情况下分别提高了3与4.5 mm,但SHAO站的对流层计算平均精度下降约5 mm,其原因就是接收机钟差和对流层参数之间的负相关性大大增加了。由图5可知,固定测站坐标后,接收机钟差与对流层参数之间的平均相关系数(坐标收敛后)由-0.2左右变为-0.43左右。大量数据计算表明,如果接收机钟差呈线性变化,则固定测站坐标后对流层参数的精度略有提高;如果接收机钟差呈随机变化,则固定测站坐标后对流层解算精度有可能下降。
3 实时卫星钟差对天顶对流层延迟的影响
采用2012-07-21北京房山区和北京市区两台站(BJNM和BJFS)的观测数据,利用IGS最终钟差产品,剔除卫星钟差粗差后解算出这两个测站的对流层延迟,如图6。

图6 剔除卫星钟差粗差的对流层延迟Fig.6 ZTD after deleting bad satellite clock error
从图6知,BJNM和BJFS两区域的对流层变化趋势大致相同,但房山区的天顶对流层延迟较大,与气象机构所发布的当天房山地区降雨量最大的事实吻合。
RTPP生成的卫星钟差采用单历元估计算法,由几大机构取加权平均值得到,其中误差约为0.1~0.15 ns[11]。IGS 发布的超快卫星轨道(igu)包括两部分,实时对流层计算需采用作为预报值的后部分,预报部分随着时间的推移,其精度随之降低[12],但偏差不会超过5 cm。在利用igu组合轨道和RTPP的卫星钟差计算实时对流层延迟参数时,如果给予的接收机钟差噪声过小,则会导致精密单点定位过程中估计参数出现跳变的情况。计算结果表明,所估计的参数中接收机钟差与利用IGS最终产品得到的解差别较大,其计算结果如图7所示。
引起上述接收机钟差解算结果差异较大的原因由卫星钟差的变化所引起,卫星钟差在30 s内的变化通常不超过1 dm,而RTPP提供的钟差变化有可能达几百米,这时需对接收机钟差给予合理的过程噪声(大于卫星钟差跳变的平方),以提高解算结果的准确性。给予30 s采样间隔历元间250 000 m2的接收机钟差噪声后所得到的单天对流层延迟如图8所示。
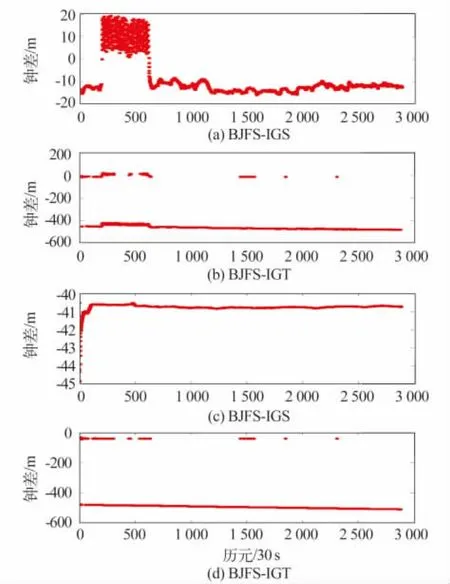
图7 最终接收机钟差与实时估计钟差Fig.7 The final receiver clock error and real time receiver clock error
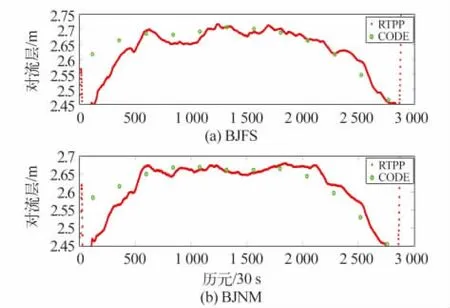
图8 调整后的实时对流层结果Fig.8 Real time ZTD after adjustment
在初始阶段,由于RTPP钟差和预报轨道的精度相对较低导致收敛时间延长,但在收敛后与CODE的最终对流层延迟符合较好。统计结果表明,在收敛后BJFS站实时对流层与最终对流层平均相差1.5 cm,BJNM 站相差1.1 cm,BJFS站精度稍差,可能是由于没有观测到P1码导致数据预处理不完善而引起。以上结果与采用最终产品解算得到的精度相差较小有关。
利用北京两测站的数据解算结果表明,北京区域7月23日暴雨前5 h(GPS时,对应北京时约为8:00~13:00)对流层持续变化为15~20 mm/h,这意味着从当日2时起持续4 h发生暴雨的可能性极大[13],这与实际情况吻合。多个台站多天的数据计算表明,利用实时卫星钟差以及预报轨道计算得到的对流层延迟误差约为1.5~2 cm,对应的水汽计算精度约为2~3 mm,可满足实时气象预报的要求。
4 结语
1)若接收机钟单独在相位或者伪距观测量发生钟跳,须利用伪距重新初始化钟差参数,以提高对流层的解算精度。
2)固定测站坐标不一定能提高对流层的解算精度,其原因是固定测站坐标后,对流层参数和卫星钟差参数的相关性大大提高,容易相互吸收。但实验表明,如果接收机钟差呈线性变化,则该方法可以改进对流层参数的解算精度。
3)合理利用RTPP卫星钟差可以得到约1.5~2 cm的实时对流层解算精度,其对应的水汽计算精度能满足实时气象预报的要求。
1 Bevis M,et al.GPS meteorology remote sensing of atmospheric water vapor using the global positioning system[J].Journal of Geophysical Research,1992,97(D14):15 787 -15 801.
2 Rocken C.GPS/STORM -GPS sensing of atmosphere water vapor for meteorology[J].Journal of Atmospheric and Oceanic Technology,1995(12):468 -477.
3 Duan Jingping,Bevis M.GPS meteorology direct estimation of the absolute value of precipitable water[J].Journal of Applied Meteorology,1996,35:830 -838.
4 徐韶光,等.利用地基GPS获取实时可降水量[J].武汉大学学报:信息科学版,2011,36(4):407 -411.(Xu Shaoguang,et al.Real - time PWV obtained by ground GPS[J].Geomatics and Information Science of Wuhan University,2011,36(4):407 -411)
5 Kouba J,Heroux P.Precise point positioning using IGS orbit and clock products[J].GPS Solutions,2001,5(2):12 -28.
6 张小红,等.基于GPS非差观测值估计大气可降水量[J].武汉大学学报:信息科学版,2010,35(7):806-810.(Zhang Xiaohong,et al.Near real time PW inversion based on zero differenced GPS observayion [J].Geomatics and Information Science of Wuhan University,2010,35(7):806 -810)
7 Dousa J.The impact of errors in predicted GPS orbits on zenith troposphere delay estimation [J].GPS Solute,2010,14(3):229-239.
8 Bohm J,Heinkelmann R,Schuh H.Short:A global model of pressure and temperature for geodetic applications[J].Journal of Geodesy,2007,81(10):679 -683.
9 Welch G,Bishop G.An introduction to Kalman filter[R].Department of Computer Science,Univ North Carolina at Chapel Hill.,TR -95 -041.1997.
10 Freymueller J T.IGSMAIL -4318:New version of clockprep program[M].IGS Central Bureau,2003.
11 IGS real time analysis center products[EB/OL].http://www.rtigs.net/products.php.
12 Agrotis Loukis,et al.RTPPP analysis results:Achievements and challenges[C].EGU General Assembly 2010,Vienna,Austria,2010.
13 曹云昌,方宗义,夏青.GPS遥感的大气可降水量与局地降水关系的初步分析[J].应用气象学报,2005,16(1):54 -59.(Cao Yunchang,Fang Zongyi,Xia Qing.Relationship between GPS precipitable water vapor and precipitation[J].Journal of Applied Meteorological Science,2005,16(1):54-59)
致谢 感谢SOPAC、CCDIS、CODE提供观测文件、IGS产品、坐标、测站日志信息,以及对流层延迟产品。
EFFECTS OF RECEIVER AND SATELLITE CLOCK ERROR ON DYNAMIC ATMOSPHERIC DELAY SOLUTION DURING PPP
Xu Shaoguang,Xiong Yongliang and Li Peng
(Department of Surveying,Southwest Jiaotong University,Chengdu 611756)
The features of receiver clock and satellite clock are the key factors to affect the precision of zenith total zenith delay when ZTD is computed by zero-difference precise point positioning.Experiments show that solution precision of troposphere parameter is largely affected by the clock jump.A reasonable strategy for this is given.Under the circumstance of site’s coordinates being fixed,the relation between receiver clock and ZTD parameters are enhanced,and ZTD’s precision will reduce with reduction of receiver clock precision,vise versa.The result analyzed 7.21data from Bejing and Fangshan stations indicates that real time PWV can be derived by IGS predicted product and PPP skill,and corresponding precision reaches 2 - 3 mm,which can satisfy the need of weather forecast.
precise point positioning;receiver clock error;satellite clock error;atmospheric delay;inversion
P228.41
A
1671-5942(2014)03-0086-05
2013-09-28
国家自然科学基金项目(40874015,41274044,41104007)。
徐韶光,男,1983年生,博士生,现主要从事高精度GPS软件开发、GNSS水汽反演及地壳形变监测研究。E-mail:sgxu@my.swjtu.edu.cn。
