导航系统中的对流层延迟效应分析

2018-06-13张洁寒杨向宇杜全成李爽

全球定位系统 2018年2期

张洁寒,杨向宇,杜全成,李爽

(河南师范大学电子与电气工程学院,河南新乡453007)

0 引言

卫星导航系统可以为用户实现定位和测速等功能,已在各个领域得到了非常大的应用,其中,应用最为广泛的是美国的GPS[1-3]。为了不受特殊情况下应用的限制,我国自主研制的区域性卫星导航系统——北斗卫星导航系统已经历了两代,其中,第一代北斗导航系统(BDS)于2003年开始运行,第二代北斗导航系统于2012年底开放运行。目前,北斗卫星系统运行稳定、工作状态良好,已在渔业、气象、交通管理运输、应急救援等方面获得了很好的应用[4-5]。

为了提高北斗卫星导航系统的定位精度,需对影响其定位精度的所有误差源进行分析和误差修正。由于对流层大气是其重要的误差源之一,因此必须对其引起的折射误差进行修正或改正。对流层引起卫星定位误差主要是由对流层环境中的折射率及其梯度的变化所引起,在雷达领域常称为对流层折射误差,在卫星领域又常称为对流层延迟,它指对流层使得无线电波的传播距离产生了延长,也相当于卫星信号到达时间产生了延迟,或时间增加。目前国内外对流层延迟的改正大都是采用模型法,即利用对流层延迟模型进行计算,常用的有UNB3、Hopfield、Black和Saastamoinen对流层延迟改正模型[6-7]。几乎所有的对流层延迟模型都是首先通过各种统计方法得到较为精确的天顶延迟,然后再采用与卫星的高度角有关的映射函数得到不同高度角下的对流层延迟。实际应用中,卫星正好在用户的天顶位置是很少见的,绝大多数都有一定的高度角,因此,天顶延迟模型和映射函数的精度决定了对流层延迟改正模型的精度,直至影响卫星的定位精度。

卫星信号通过对流层产生的折射误差由无线电波在对流层中传播的机理决定,要对卫星系统的对流层延迟进行预测和计算,就必须搞清折射误差的来源,分清产生对流层折射误差的各个因素及其所占比重,从而提高计算对流层延迟的精度。本文针对北斗卫星在各种位置的情况,根据卫星信号在对流层中的传播机理,分析了引起对流层延迟的两个效应,以及这两个效应在不同高度角下所引起折射误差的比重,为北斗卫星对流层延迟改正提供参考。

1 产生对流层延迟的效应分析

对流层是非色散介质,无线电波在其中传播的相速与群速相等。由电波传播理论可知,无线电波在对流层大气中传播时,大气的不均匀性使得电波在传播时产生折射效应。电波的折射效应一是使得电波射线不按直线传播,而是依据相邻两层大气间折射率的变化而按不同的曲线传播,从而使得电波传播的路径变长。二是由于对流层大气中的折射率n大于真空中的折射率1,电波在对流层中不再是按真空中的光速c,而是以小于c的c/n速度传播,从而使得传播时间增大,或称为时间延迟。

由于对流层大气在水平方向上的变化远远小于垂直方向上的变化,因此常将对流层大气假设为球面分层大气[8],地面到目标电波传播示意图如图1所示[9]。

假设地面用户O到目标T的真实电波弯曲射线长为l,则经历dl弧长所用时间dt为

(1)

则从地面用户h0到目标高度hT经历的时间t为

(2)

式中:n为大气折射率;θ为电波射线仰角;Rg为电波曲线的几何长度。

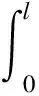
(3)

根据无线电测距原理,无线电测量到的地面到目标的距离Re为[10]

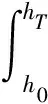
(4)

假设地面到目标的真实距离(直线几何距离)为R0,则由于对流层大气对电波的折射效应引起误差(常称为折射误差)ΔR为

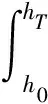
=ΔRd+ΔRb,

(5)

(6)

式中,ΔRd与大气折射率有关,它是由电波传播速度减慢(速度为c/n)而产生的对流层折射误差; ΔRb只与电波射线的角度θ有关,而与大气折射率无关,它是由电波射线弯曲而产生的对流层折射误差。可见电波传播速度延迟和电波射线弯曲两种效应都会产生折射误差。

由于电波射线弯曲也相当于传播路径的增加,增加的路径也相当于传播时间上的延迟,因此在卫星导航系统应用中常将对流层折射误差称为对流层延迟。在实际应用中,为了减小卫星定位误差,提高其精度,就需要精确计算出对流层延迟。这就需要精确地计算出电波传播速度减慢和电波射线弯曲两者引起的总对流层延迟,或称为总折射误差。

从式(6)可以看到,由于电波传播速度减慢引起的对流层延迟ΔRd和电波射线弯曲引起的对流层延迟ΔRb都与电波射线的仰角θ有关。而根据球面分层大气中的snell定理,电波射线的仰角θ与卫星的高低角θ0有关,即[8]

n(a+h)cosθ=n0(a+h0)cosθ0,

(7)

式中:a为地球平均半径,a=6370000 m;h0、n0、θ0分别为用户地面高度、该处的大气折射率和卫星高低角;h、n、θ分别为电波射线处任意高度、该处的大气折射率和电波射线仰角。

这样,对流层延迟ΔRd和ΔRb都与卫星的高低角θ0有关,它们都随卫星高低角θ0而变化。当卫星处于不同位置时由于其高低角变化,则必定会引起对流层延迟ΔRd和ΔRb的变化。也就是说,不同的卫星高低角,电波传播速度减慢和电波射线弯曲对对流层延迟的贡献不同。

2 对流层延迟计算与分析

为了比较电波射线弯曲和传播速度减慢两种效应产生的对流层延迟情况,根据我国大气分布情况,对流层大气折射率剖面在冬季变化较小,在夏季变化较大,因此这里选择了郑州地区2017年1月份(代表冬季)、7月份(代表夏季)的两组大气探测实测数据进行对流层延迟的计算。利用式(6)计算出电波传播速度减慢引起的对流层延迟ΔRd和电波射线弯曲引起的对流层延迟ΔRb。为了提高计算精度,积分项采用高斯-勒让德数值积分进行。

假设对流层顶高度为60 km,并假设卫星的高度角分别为1°、2°、3°、4°、5°、7°、10°、20°,计算出的电波传播速度减慢引起的对流层延迟ΔRd、电波射线弯曲引起的对流层延迟ΔRb、对流层折射引起的总延迟ΔR,以及它们各占总延迟的比率等参数如表1所示。

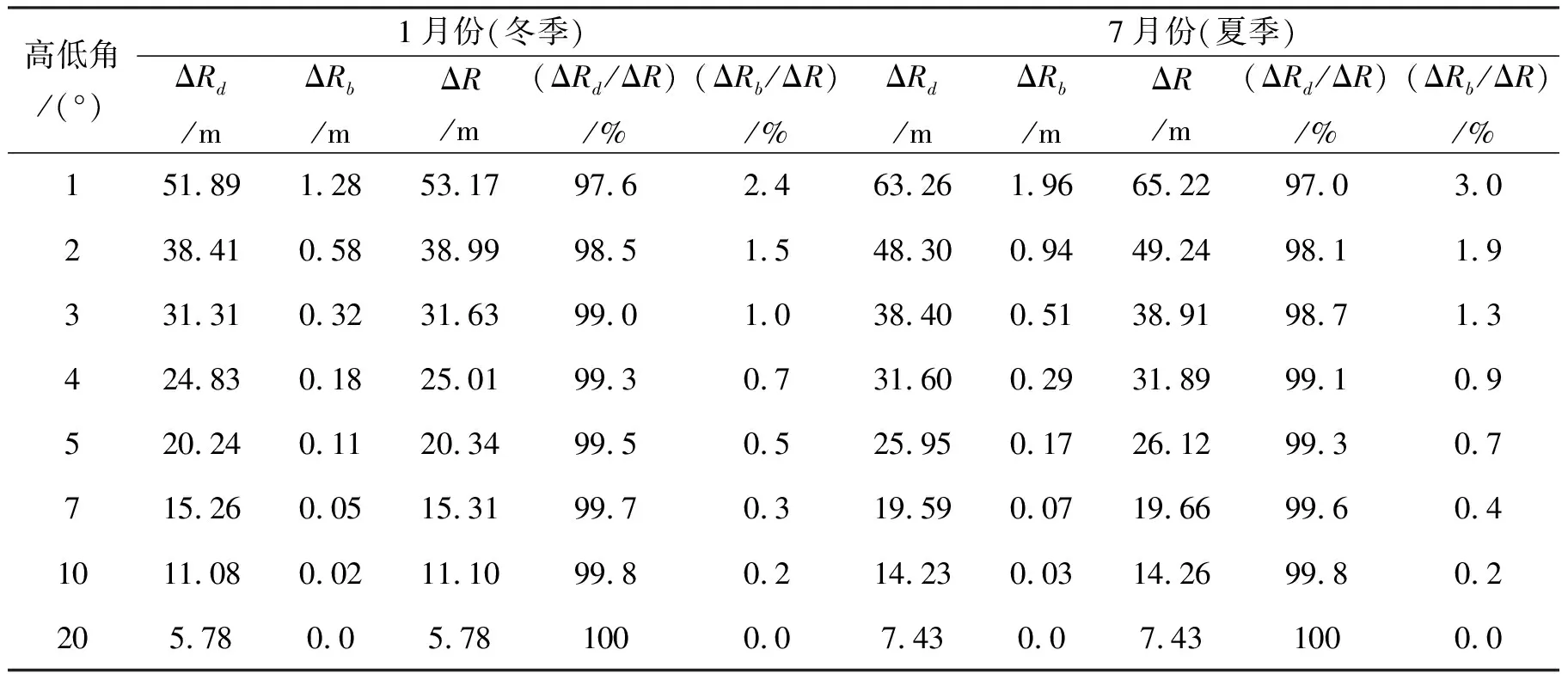
表1 对流层延迟计算

由表1可见,对流层大气引起的延迟ΔR随卫星高度角的增大而减小;电波传播速度减慢引起的对流层延迟ΔRd远大于电波射线弯曲引起的对流层延迟ΔRb,且随着卫星高度角的增大,电波射线弯曲引起的对流层延迟ΔRb很快趋于0.当高低角大于20°以上时,电波射线弯曲引起的对流层延迟几乎为0。当高低角大于3°(冬季)、4°(夏季)以上时,电波射线弯曲引起的对流层延迟占总对流层延迟的1%以下。