自适应检测窗伪码捕获算法*
2017-11-01贺杰,张斌
贺 杰, 张 斌
(空军工程大学信息与导航学院, 西安 710077)
自适应检测窗伪码捕获算法*
贺 杰, 张 斌
(空军工程大学信息与导航学院, 西安 710077)
针对长伪码序列捕获中滑动串行捕获算法计算复杂度过高的问题,提出了一种自适应检测窗伪码捕获算法。该方法通过在不同信噪比条件下自适应构建检测窗,快速确定其在接收伪码序列中的位置信息,直接生成与接收伪码序列粗同步的本地伪码序列,完成捕获。仿真结果表明该方法大大降低计算复杂度并能在低信噪比条件下稳定工作。较之滑动串行捕获算法,该方法有更低的硬件实现复杂度,易于工程实现。
自适应检测窗;计算复杂度;长伪码序列捕获
0 引言
近年来,扩频通信由于抗噪能力强、易实现码分多址和安全通信等优异性能已被广泛应用于导航与通信领域。由于扩频多由长伪码序列扩展频谱实现,因此,长伪码序列的捕获成为整个系统十分关键的问题。
当前常用的伪码捕获算法有滑动串行捕获算法、并行捕获算法、串并混合捕获算法、频域变换捕获算法及迭代检测捕获算法等。如何兼顾捕获时间和算法实现复杂度,成为工程实现需考虑的重要问题。滑动串行捕获算法对每个码相位进行滑动相关搜索,实现简单,对系统资源消耗少,但捕获速度慢,捕获时间对码长较为敏感。并行捕获是对所有码相位同时进行搜索,捕获时间短,但实现复杂度高,需消耗大量硬件资源。为兼顾捕获速度和硬件复杂性,文献[1-2]提出了串并结合的大步进搜索伪码捕获方案,对码相位进行分段并行搜索,是全串行和全并行捕获的折中处理。文献[3]采用基于FFT的频域捕获算法,能实现快速捕获,但需消耗大量硬件资源。文献[4-5]提出了采用迭代消息传递的思想进行伪码捕获,是对接收序列的一种最大后验估计,该方法能在硬件复杂度适中的情况下实现对伪码的快速捕获,但对接收信噪比较为敏感。
文中在传统捕获算法的基础上提出了一种自适应检测窗伪码捕获算法。算法基于检测窗(初始状态量)结构的构建,并确定检测窗在接收伪码序列的位置,直接产生出伪码序列,实现伪码序列的捕获。分析及仿真结果表明:该算法的硬件实现复杂度较低,计算量较串行捕获有较大降低,易于工程实现。
1 自适应检测窗伪码捕获算法
1.1 伪码捕获的数学基础
伪码捕获是基于其良好的自相关特性。在数学上用自相关函数来表示信号与它自身相移以后的自相关,其定义为:
(1)
式中:x(t)为信号时间函数;τ为时间延迟,x(t-τ)为时间上向右平移τ后得到的波形;自相关函数Rx(τ)衡量x(t)与它自身平移后的波形x(t-τ)两者之间的相似程度。对于周期性的伪码序列z(t)而言,它的自相关函数计算可依据式(1)进行,但可以简化成:

(2)
式中:N为伪码序列周期长度;Tc为一个码片的持续时间。当τ为Tc的整数i倍时,上式可进一步表达成如下的离散型形式:
(3)
如图1所示,二进制伪码序列的自相关函数Rz(τ)(归一化后)在原点中心呈一个三角形。这表明当τ=0时,两信号完全相同,此时具有最大的相关值,当|τ|≥Tc时,Rz(τ)=0。利用这种良好的自相关特性,很容易判断接收信号和本地信号之间的相位是否一致,从而实现伪码的捕获。
1.2 信号基本模型
文中接收信号模型考虑经过BPSK调制的基带扩频信号模型:
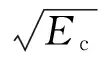
(4)
式中:yk为经过高斯加性白噪声信道的信号采样序列值;Ec为每个发射码片的能量;xk为采样时刻k的伪码序列值;nk为服从N(0,N0/2)分布的噪声采样序列。
1.3 算法结构分析
注意到,要恢复一段伪码序列,只须知道产生该伪码序列移位寄存器的初始状态量,且知道该状态量在这段伪码序列中的位置,通过向前向后迭代即可恢复出伪码序列。
因此,算法的实现思想是:先构建检测窗,检测窗实质上是本地伪码的一段序列,通过检测窗序列与接收序列进行滑动相关,当出现相关峰值时,便可确定检测窗序列在接收序列中的位置,然后取检测窗序列部分序列作为移位寄存器的初始状态并结合其在接收序列中的位置信息,根据伪码的本原多项式,直接生成与接收伪码序列粗同步的本地伪码序列,实现伪码捕获。检测窗序列滑动相关定位的示意图如图2。
检测窗长度的选择根据具体环境中信噪比的变化,自适应调整检测窗长度的设置,以动态地减少相关计算量。算法的实现原理如图3。
捕获系统有3种工作状态:调整状态、相位搜索状态和伪码恢复状态。当系统处于调整状态时,主要对检测窗结构和捕获判决门限进行动态调整。在调整支路选用了一个与接收信号正交的检测窗序列,将其与接收信号的相关值作为窗内的噪声功率估计,将窗内噪声功率送到检测窗结构构建模块,按照相应的构建算法完成检测窗结构的构建,同时将窗内噪声功率送到捕获判决模块以动态调整判决门限,增强整个捕获系统的抗噪性能。待系统完成调整状态后进入到相位搜索状态,滑动检测窗进行相关检测,当出现相关峰值时,将位置信息和移位寄存器初始状态信息送入到伪码恢复模块,进入伪码序列恢复状态,恢复出伪码序列,算法流程如图4。
图4 自适应检测窗伪码捕获算法流程图
2 自适应检测窗结构设计
检测窗结构构建是否适当,是影响捕获性能的一个重要因素。在实际情况中,由于信道的衰落、干扰和噪声的影响,固定检测窗不能适应接收信号的强弱变化。若判决门限设定的太低,当信号比较强时容易错锁在序列互相关或自相关旁瓣上;若判决门限设置太高,弱信号可能无法进行捕获。
为避免上述情况,文中采用基于噪声功率估计的自适应检测窗结构设计。即当信号比较弱时,检测窗的序列长度自动加长;信号比较强时,检测窗的序列长度自动调低。
这种方法实现思路是:依据接收信号的N个采样值,对落入到检测窗内的噪声功率作出估计,这个估计值加上一个固定值作为检测窗内信号功率值。通过检测窗内信号功率的估计值可计算得到检测窗的序列长度,从而完成检测窗的构建。通过仿真实验可知当检测窗内信号功率比噪声功率大3 dB时,即可实现可靠检测。其原理如图5所示。
接收序列y1,y2,y3,…,yn是连续n个采样值。
yk=ACPN(k-τ)+N(k)
(5)
式中:A为接收信号幅度;CPN(k-τ)为接收伪码序列;N(k)为信道中的加性白噪声;τ为码相位延时。选用了一个与yk正交的检测窗序列CPN(k-τ1)相乘,记为Pn,利用伪码序列良好的自相关特性,则:
(6)
这个结果是检测窗内的噪声功率估计,正是期望得到的结果。显然,判决门限是随接收信号信噪比变化而改变的,每隔一段时间可以更新一次门限,这样体现了信号和噪声能量大小的变化,减小了漏检概率。
3 仿真结果及分析
文中对不同信噪比条件下伪码捕获情况进行了仿真,统一的仿真条件为:10级、9级、8级伪码序列的本原多项式分别为:
g10(x)=1+x3+x10
(7)
g9(x)=1+x4+x9
(8)
g8(x)=1+x2+x3+x4+x7
(9)
每个码片的采样次数为1次,仿真结果如下。
3.1 检测窗长与信噪比的关系
如图6所示为10级、9级、8级伪码序列检测窗长随信噪比的变化曲线。由图6可以看出,随着信噪比的不断增大,检测窗的长度不断减小。在小信噪比端,随着信噪比的增加,检测窗长迅速减小,当信噪比增大到0 dB后,检测窗长随信噪比的增加减小变缓。可见检测窗长与信噪比成负相关关系,也反映出了检测窗长自适应信道变化情况。小信噪比下,通过增加窗长,以增大捕获概率;大信噪比下,在保证捕获概率的前提下,减小检测窗长,以减小计算复杂度和捕获时间。
3.2 计算复杂度改善情况
表1给出了不同码长情况下,滑动串行捕获和自适应检测窗捕获运算复杂度及不同信噪比下自适应检测窗捕获对计算复杂度的改善效果。其中改善效果以自适应检测窗捕获算法减少计算量占滑动串行捕获计算量的百分比来衡量。
从表1中可以看出,大信噪比条件下,检测窗短,改善效果好。当伪码序列长度为1 023时,串行捕获需进行2 092 035次乘加运算,而自适应检测窗捕获算法,在噪比为7 dB时,检测窗长度仅为93,捕获需进行189 255次乘加运算,计算量仅为串行捕获的9%,极大的减少了计算量。
图7给出了文中算法对不同级数伪码序列改善效果随信噪比的变化示意图。从图中可以看出改善效果与信噪比成负相关关系,信噪比越大,改善效果越好,在信噪比相同的情况下,码长越长,改善效果越好。当码长为1 023(级数为10),信噪比为-10 dB时,改善效果仍在60%以上,255时(级数为8),改善效果已下降到20%以下。文中算法对长伪码序列捕获计算量的改善有更好的效果。

而相同信噪比下码长为
3.3 捕获性能分析
捕获概率是1 000次考察样本下得到的。图8给出了几种不同捕获方法下,级数为10的伪码序列捕获概率随信噪比的变化示意图。从图中可以看出,固定窗长的捕获概率随着信噪比的减小而不断恶化,而自适应窗长捕获时,捕获概率和串行捕获相当,始终保持在100%,捕获性能很稳定。
图9给出了SNR=-7 dB,几种不同窗长下捕获级数为8的伪码序列时及滑动串行捕获时相关峰增益值的示意图。从图中可以看出当检测窗长为30时,相关增益峰值较低,信号被噪声淹没,无法实现可靠检测,继续增加窗长后,相关增益峰值增大,当窗长增加到163时,便可实现可靠检测,但相比滑动串行捕获时的相关增益峰值,检测窗捕获的相关增益峰值明显较低。
检测窗捕获实际上是以牺牲相关增益来换取计算复杂度的降低,仿真实验表明在保证可靠捕获的前提下,适当地牺牲相关增益是可以接受的。
4 结束语
实际信道环境十分复杂,为兼顾捕获速度和实现复杂度,文中提出了一种自适应检测窗伪码捕获算法,分析了算法结构及流程,通过构建自适应检测窗,减小计算复杂度。通过仿真实验验证,该方法能较好的根据接收信号信噪比的变化调整窗结构和判决门限,在大信噪比下能较大的减少计算量,实现复杂度进一步降低,易于工程实现。但对于复杂电磁环境,只针对信噪比变化和白噪声情况进行仿真,没有考虑多普勒频移、多径和其它噪声情况下捕获方法的性能,这些是文中进一步深入研究的方向。
[1] 王伟, 徐定杰, 沈峰. 一种大步进伪码快速捕获方法的研究 [J]. 哈尔滨工程大学学报, 2006, 27(5): 721-727.
[2] 陈实如, 张京娟, 孙尧. 直扩系统伪码序列串并组合捕获方案 [J]. 哈尔滨工程大学学报, 2003, 24(1): 54-59.
[3] 罗炬锋, 王翔, 付耀先, 等. 基于FFT并行搜索伪码和频偏的快速捕获新方法 [J]. 电子信息学报, 2011, 33(3): 563-568.
[4] 王伟, 刘洋, 李欣. 基于迭代信息传递的PN码快速捕获方法研究 [J]. 宇航学报, 2008, 29(4): 1375-1380.
[5] CHUGG K M, ZHU Mingrui. A new approach to rapid PN code acquisition using iterative message passing techniques [J]. IEEE Journal on Selected Areas in Communication. 2005, 23(1): 884-897.
[6] 赵志远, 陈树新, 华璐. 基于信噪比控制的自适应伪码捕获算法 [J]. 空军工程大学学报(自然科学版), 2013, 14(5): 80-84.
[7] 王超亮, 李擎, 苏中. 高速GPS接收机信号捕获算法研究 [J]. 测控技术, 2014, 33(2): 20-23.
[8] CHAWLA K K, SARWATE D V. Parallel acquisition of PN sequences in DS/SS systems [J]. IEEE Transactions on Communications, 1994, 42(6): 2155-2164.
AlgorithmforofPNCodesBasedonSelf-adaptiveDetectionWindow
HE Jie, ZHANG Bin
(Information and Navigation College, Air Force Engineering University, Xi’an 710077, China)
As the high computational complexity of sliding serial acquisition algorithm in the process of long PN sequence acquisition, an PN code acquisition algorithm for self-adaptive detection window was proposed. Through constructing self-adaptive detection window under the condition of different SNR, this method could quickly determine the position information in the process of receiving PN sequence, and the local PN sequence which was coarse synchronizing with the
PN sequence was directly generated to complete acquisition. Simulation results showed that this method could greatly reduce the computational complexity and could work steadily under the condition of low SNR. Compared with sliding serial acquisition algorithm, it had lower hardware implementation complexity, and it was easy to implement.
self-adaptive detection window; computational complexity; long PN code acquisition
TN914
A
2016-09-04
国家自然科学基金(61273048)资助
贺杰(1993-),男,湖南常德人,硕士研究生,研究方向:军用无线电导航。
