一种DSSS系统自适应门限分析模型*
2017-11-01费顺超冯永新张笑宇
费顺超, 冯永新, 刘 芳, 张笑宇
(沈阳理工大学, 沈阳 110159)
一种DSSS系统自适应门限分析模型*
费顺超, 冯永新, 刘 芳, 张笑宇
(沈阳理工大学, 沈阳 110159)
自适应门限是影响直接序列扩频(DSSS)系统平均捕获时间的关键因素。为达到降低DSSS系统平均捕获时间的目的,文中通过深入分析非相干累加与虚警概率、检测概率、平均捕获时间的关系,建立了一种DSSS系统自适应门限分析模型。仿真结果表明,该分析模型可通过自适应门限阈值来有效降低DSSS系统的平均捕获时间,进而为工程应用中的门限自适应提供理论依据。
直接序列扩频;捕获;自适应门限;分析模型
0 引言
在现代战场环境中,如何在弹药与指挥控制系统、弹药与发射平台、弹药与弹药之间,建立安全、可靠的数据通信链路,成为军事保密通信研究的热点。在军事通信设备和系统中,直接序列扩频通信系统(DSSS)凭借其在保密性、抗干扰性的突出特点,在保密通信中占有重要地位,而同步又是其的关键环节。作为同步的重要性能指标,平均捕获时间决定着系统的传输时效性。在复杂环境中,若采用固定门限判决方法,信号的虚警概率增加、检测概率减小将导致通信系统无法正常工作。而自适应门限技术,可使判决门限根据环境动态调整,满足系统对虚警概率的需求,保证数据传输的时效性。
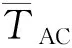
1 自适应门限算法原理
鉴于二进制相移键控(BPSK)为DSSS系统的典型应用,以BPSK调制为例,进行自适应门限算法分析。设接收信号通过下变频后的中频信号为:
r(k)=A·D(k)·C(k)·cos(ωck+Δφ)+N(k)
(1)
式中:D(k)表示调制的数据信息;C(k)表示伪随机序列;k为采样时刻;ωc表示中频载波;A表示信号幅度;N(k)表示均值为0、方差为σ2的高斯随机白噪声;功率谱密度为N0。
自适应相关捕获原理如图1所示。接收信号通过同相、正交支路后,经过去载波、解扩后平方累加得到检验统计量。自适应门限估计中可通过MLAP、OSAP、AAP等方法得到的自适应门限估计值与统计量进行对比判决,输出判决结果。
H0:本地码与接收信号未对齐时无法捕获信号,其概率密度函数为:
(2)
H1:本地码与接收信号对齐时,其概率密度函数为:
P1(Z)=P(Z|H1)=
(3)
式中:V=2σ2;SNR=A2/V为信噪比;In-1(x)是第一类n-1阶修正贝塞尔函数[10]。根据式(2)、式(3),可得虚警概率Pf、检测概率Pd为:

(4)
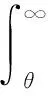
(5)
当信道模型为瑞利衰落信道时[7,10],接收信号的统计特性发生变化。若非相干累加量为L,可得检测门限θ条件下的虚警概率和检测概率为:
(6)
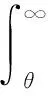
(7)
由式(4)、式(6)可知,当本地信号与接收信号未对齐时,高斯信道和瑞利信道下系统虚警概率相同,可归为一类讨论。由式(6)可根据设定的虚警概率得到累加次数与θ/V的关系,再根据式(7)可以得到检测概率Pd与非相干累加量L的关系。
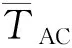
2.1 平均捕获时间目标函数
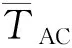
(8)
式中:NT为伪随机序列周期;TD=n·TC(0 (9) (10) 2.2 非相干累加量求解 考虑统计分析的低信噪比环境,信噪比估计可采用基于NDA(non-data-aided)最大似然估计的梯度迭代求解方法[13],噪声的估计采用最大似然估计方法[14]。为此,自适应门限估计原理框图,如图2所示。 1)接收信号r(k)通过I、Q支路得到统计检测量Z,通过信噪比估计及噪声估计得到信噪比SNR和噪声方差V。 2)在恒虚警系统中,根据系统设定的Pf,由f函数,即式(4)、式(6),可得θ/V与L的关系。当L=2时由朗伯W函数求得θ/V,当L>2时,由曲线拟合技术求得θ/V。 3)根据步骤2)求得的L与θ/V对应关系,结合分析模型中的Pd检测概率公式,可求得特定信道环境下用L表示的检测概率Pd。 5)由得到的LC控制非相干次数。同时,由恒虚警系统θ/V与L的关系,得到LC次非相干累加对应的(θ/V)LC,并与最大似然估计的噪声方差相乘,得到恒虚警门限值θ。 为了验证文中提出模型的有效性,进行以下仿真。首先,仿真不同信噪比条件下检测概率与累加量的关系。设定系统的虚警概率Pf=0.01,伪随机序列周期NT=1 024,信道中信噪比分别等于-6 dB、-2 dB、2 dB,非相干累加量变化范围是1~20,信道仿真环境为高斯信道和瑞利信道,各个累加量分别测试1 000次。检测概率与累加量关系的理论分析及仿真结果如图3~图4所示。 由图3~图4可知,系统检测概率随着积累次数的增加而逐渐增大,并最终趋近于1。当信道中信噪比逐渐变小时,检测概率的增长速度发生变化。根据图3高斯信道下仿真结果,当信道中信噪比为-6 dB时,通过累加12次可以使检测概率大于0.9。相同仿真环境下,当信噪比为-2 dB时,若使检测概率大于0.9,则需要的累加次数为6。在瑞利信道中,当信噪比为-2 dB时,检测概率大于0.9时需要累加15次。当累加量大于19时,非相关累加对检测概率不再发生作用。由于瑞利信道衰落的影响,在相同环境下,若得到相同的检测概率则需要更多的非相干累加次数。综上,在低信噪比环境下,可通过增大非相干累加量提高信号的检测概率,通过非相干累加得到一定的解扩增益。 另外,虚警概率、检测概率、非相干累加量的变化会影响系统平均捕获时间。当虚警概率为0.001时,平均捕获时间与非相干累加的关系如图5~图6所示。 平均捕获时间随着非相干累加量的变化先变小后变大。当高斯信道和瑞利信道下的非相干累加量分别为5和7时,可分别得到当前仿真环境的最短平均捕获时间。其中,虚警概率、检测概率的变化会影响到非相干累加量的选择,不同信噪比环境下的非相干累加量与平均捕获时间的关系如图7~图8所示。 根据图7~图8,在高斯信道和瑞利信道环境下,平均捕获时间随着累加次数的变化而变化。对于高斯信道,当SNR=-10 dB时,系统所需的平均捕获时间随着累加量的增加而减小。当L>16时,平均捕获时间趋于平稳。当SNR=-6 dB时,累加量为8时需要的平均捕获时间最少。当SNR=-2 dB时,累加量为4时平均捕获时间最少。当SNR=2 dB时,平均捕获时间随着累加量的增大而变大,非相干累加没有改善系统的平均捕获时间。因此,由关系图7可知,当信噪比较小时,可通过适当增加非相干累加量的方法缩短平均捕获时间。当平均捕获时间最短时,由分析模型可得系统的最优非相干累加量LC。由反馈至f(·)关系函数得到的LC次非相干累加对应的(θ/V)LC,与最大似然估计的噪声方差相乘,可以得到恒虚警门限阈值θ。 对于瑞利信道,系统平均捕获时间与非相干累加关系图8趋势相同。但相同参数条件下,由于瑞利信道检测概率低于高斯信道信号的检测概率等原因,系统平均捕获时间较高斯信道明显增大。 文中通过对高斯信道和瑞利信道下的统计量的分析,建立了非相干累加量与平均捕获时间的分析模型。仿真结果表明,非相干累加量可以提高系统的检测概率,当直扩数据链通信系统对检测概率有特殊需求时,可通过累加控制器调节非相干累加量。同时,非相干累加量、虚警概率、检测概率及信道环境共同决定系统的平均捕获时间, [1] DAI Weihua, QIAO Chunjie, WANG Yueke, et al. Improved anti-jamming scheme for direct-sequence spread-spectrum receivers [J]. Electronics letters, 2016, 52(2): 161-163. [2] KIM C J, LEE H J, LEE H S. Adaptive acquisition of PN sequences for DSSS communications [J]. IEEE Transactions on Communications, 1998, 46(8): 993-996. [3] NIR Le V, SCHEERS B. Robust blind carrier frequency synchronization for direct sequence spread spectrum systems [J]. Electronics letters, 2015, 51(5): 425-427 [4] KIM C J. Adaptive acquisition of PN code in multipath fading mobile channels [J]. Electronics Letters, 2002, 38(2): 135-137. [5] HAN Yu, JIA Guozhu. Adaptive acquisition threshold algorithm based on mean energy [C]// 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control (IMCCC).[S.l.:s.n.], 2013. 634-637. [6] 吴玉成, 陈宁, 高珊. 突发通信中的自适应门限信号检测方法 [J]. 电子与信息学报, 2007, 29(12): 2896-2898. [7] 安勇, 牟荣增, 阎跃鹏. 自适应非相干累加次数和门限的捕获策略研究 [J]. 系统仿真学报, 2011, 23(4): 817-820. [8] VITERBI A J, CDMA: principles of spread spectrum communication [M]. MA: Addison Wesley,1995: 366-368. [9] YEOM Soonam, JUNG Yunho, LEE Seongjoo. An adaptive threshold technique for fast PN code acquisition in DSSS systems [J]. IEEE Transaction on Vehicular Technology, 2011, 60(6): 2870-2874. [10] 薛巍, 向敬成, 周治中. 一种PN码捕获的门限自适应估计方法 [J]. 电子学报, 2003, 31(12): 1870-1873. [11] 田日才, 迟永刚. 扩频通信 [M]. 北京: 清华大学出版社, 2014: 176-182. [12] 付文君, 姜景山, 王拴荣, 等. QPSK数字接收机中的SNR估计的新方法 [J]. 电子与信息学报, 2007, 29(2): 255-259. [13] 吴玉成, 陈婷婷. 在滑动窗口中判决的自适应门限检测方法 [J]. 系统仿真学报, 2008, 20(10): 2770-2773. AnAdaptiveThresholdAnalysisModelforDSSSSystem FEI Shunchao, FENG Yongxin, LIU Fang, ZHANG Xiaoyu (Shenyang Ligong University, Shenyang 110159, China) The adaptive threshold is one of the key factors influenceing the mean acquisition time. In order to decrease the mean acquisition time, an adaptive threshold analysis model was established by analizing the relationships among non coherent accumulation, false alarm probability, detection probability and mean acquisition time. Simulation result shows that using the analysis model to adjust the adaptive threshold was an effective mehtod to decrease the mean acquisiton time, which could provide theoretical basis for engineering application. DSSS; acquisition; adaptive threshold; analysis model TN914.42;TN927.23 A 2016-06-14 国家自然科学基金(61501309);辽宁省特聘教授计划;中国博士后科学基金(2015M580231)资助 费顺超(1987-),男,河北廊坊人,博士研究生,研究方向:扩频通信及电子对抗。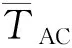
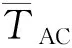
3 仿真与性能分析
4 结论

