双向S-优势粗集及其在意图识别中的应用*

张 鑫, 李续武, 路艳丽

(空军工程大学防空反导学院, 西安 710051)

双向S-优势粗集及其在意图识别中的应用*

张 鑫, 李续武, 路艳丽

(空军工程大学防空反导学院, 西安 710051)

针对传统的粗糙集模型不能有效处理具有动态特性的偏好信息系统这一缺陷,文中提出双向S-优势粗集模型。首先在双向S-粗集的基础上,引入优势关系,并将两者结合建立了基于优势关系的双向S-粗集模型。然后对该模型的性质以及该模型与优势粗糙集模型之间存在的关系进行了研究。最后通过在实例中对该模型的应用,表明该模型可成功应用于战场对敌意图识别问题。

优势粗糙集;双向S-粗集;双向S-优势粗集;意图识别

0 引言

粗糙集[1]理论是波兰华沙理工大学Pawlak教授于20世纪80年代初提出的一种研究不完整、不确定知识和数据的表达、学习、归纳的理论方法,已在知识获取、数据挖掘、决策分析等领域得到广泛应用。与此同时,许多学者对经典粗糙集模型进行了推广[2-11]。针对具有动态特性的集合X⊂U,史开泉教授提出奇异粗集(singular rough sets),简称S-粗集[6-8]。S-粗集为解决动态系统识别、动态系统决策、动态系统推理与动态证据合成等问题提供了有力的工具。而经典S-粗集处理的动态集合是基于等价关系建立的模型,因此对于具有偏好关系的信息系统则不能进行有效的处理。基于优势关系的粗糙集模型[7-9]是静态的,不能反映处于动态条件下的偏好信息系统。而现实中的很多偏好信息系统均具有动态特性。例如:在意图识别中,由于各种不确定因素的存在,使得我方面临着各种各样的威胁,人们利用一定的偏好信息对敌方作战意图进行排序并识别。但在对敌意图识别中,不确定因素并不是静态不变的,而是不断变化的,这样就使得静态的优势粗糙集不能很好的解决该类问题。

针对上面提出的问题,文中通过引入优势关系,提出基于优势关系的双向S-优势粗集模型。该模型完善了双向S-粗集模型在偏好信息系统的应用,有利于双向S-粗集从偏好信息中挖掘数据,提取规则。

1 优势粗糙集

针对传统粗糙集不能有效解决具有偏好属性的信息系统相关问题,Greco将优势关系[2]引入粗糙集,替换传统粗糙集的等价关系,从而形成了采用优势粗糙集解决偏好问题的方法,拓展了粗糙集的应用范围。

形式化的信息系统可表示为四元组IS=(U,AT,V,f),其中U是非空有限的对象集合,AT=C∪D是非空有限的属性集合,其中C为条件属性,D为决策属性。

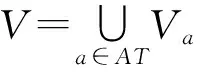
在信息系统IS中,可以根据决策属性集D将U划分为有穷个数的类集合:Cl={Clt|t=1,…,n},对任意x∈U属于且只属于其中一个分类Clt∈Cl。

定义1[2]在信息系统IS中,定义在决策属性集D下的优势集为:

(1)

其中根据决策属性划分的类集合也是有序的,也就是说对所有的r,s∈T,T={1,2,…,n}。若r>s,则Clr里的对象从决策角度来看要优于Cls里的对象。

定义2[2]对于集合P⊆C,任意q∈P,都有x≥qy,就称x在属性集P上优于y,记为xDPy。对给定的P⊆C和x∈U,定义P-dominating集为:

(2)

(3)

(4)

2 S-粗集及双向S-粗集

为了弥补Pawlak经典粗糙集在解决具有动态特征的信息系统时的不足,史开泉教授提出了S-粗集。由于具有动态特征的信息系统中,元素的动态特性表现为迁入和迁出,于是S-粗集又分为元素只具有迁入特性的单向S-粗集[5]和元素具有迁入、迁出特性的双向S-粗集。其中,单向S-粗集是双向S-粗集的特例,双向S-粗集是单向S-粗集的推广。

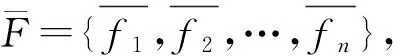
定义4[6-8]对于集合X⊂U,如果:

∉X}

(5)

则称X′为X的亏集。

定义5[6-8]对于集合X⊂U,如果:

X*=X′∪{uu∈U,u∉X,f(u)=x∈X}

(6)

则称X*⊆U是U上的一个S-集合。

定义6[6-8]对于U上的一个S-集合X*⊆U,分别称:

(R,F)o(X*)={xx∈U,[x]R⊆X*}

(7)

(R,F)o(X*)=xx∈U,[x]R∩X*≠∅

(8)

为X*的S-下近似集和S-上近似集;称集合对:

((R,F)o(X*),(R,F)o(X*))

(9)

为X*⊆U的双向S-粗集。

3 双向S-优势粗集

优势粗糙集将经典粗糙集中的等价关系替换为优势关系,弥补了经典粗糙集在处理具有偏好信息的信息系统中的不足。然而信息系统中的对象并不是静态不变的,对象会随着时间等因素的推移呈现出动态的迁移特性。

针对经典的优势粗糙集中对象并不具备迁移特性这一缺陷,文中将经典的优势粗糙集与双向S-粗集相结合,建立双向S-优势粗集模型,使优势粗糙集中的元素具有迁移特性,以更好的解决此类问题。

3.1 双向S-优势粗集模型的定义

(10)

(11)

(12)

(13)

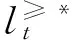
(14)

(15)

为双向S-优势粗集的正域;称:

(16)

为双向S-优势粗集的负域;称:

(17)

为双向S-优势粗集的边界域。

3.2 双向S-优势粗集模型的相关性质

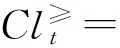
(DP,F)o(∅)=(DP,F)o(∅)=∅

(18)

(DP,F)o(U)=(DP,F)o(U)=U

(19)

性质2

(20)

性质3

(21)

(22)

(23)

(24)

性质5

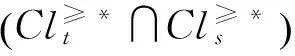
(25)

(26)

性质6

(27)

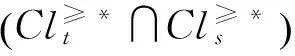
(28)

证明性质1由定义9易证;

性质2由定义9易证;

同理可证:

性质3得证;

性质4得证;

同理可证:

性质5得证;

同理可证:

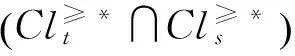
性质6得证。

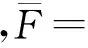
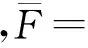
则:

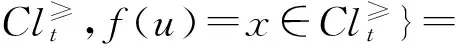
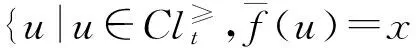
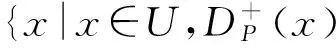
即

相应地在对敌作战意图识别的论域中,对象相对于用户群呈现的威胁程度不是一成不变的。随着时间推移,意图识别时一些评估指标用户不再关心,从评估系统中剔除,而一些新的评估指标相应也会因为用户的关注而添加到评估系统中,如此便会出现部分对象从一个威胁集迁移至另一个威胁集,即我方对敌作战意图识别结果发生变化。

4 对敌意图识别应用实例

在作战行动中,敌我之间的对抗受意图驱使。意图识别系统通过收集战场态势信息,判别敌作战意图,从而进行决策。作战意图识别类似于人工智能领域的规划识别,最早由Schmidt[12]等人于1987年逐渐提出,并逐渐成为人工智能热门研究领域。近些年,我国学者在作战意图识别领域作了大量工作[13-15],提出了用于战术意图识别的动态序列贝叶斯网络[14],基于MEBN的战术意图识别[15]等。文中从双向S-优势粗糙集的角度出发,在对目标的各项参数已经获取并已经识别出目标类型的基础上,对目标的作战意图进行识别。文中首先采用由目标识别系统得到的数据样本对意图识别系统进行训练,然后采用双向S-优势粗集的理论对目标的作战意图进行分类。

设在空袭目标作战意图识别中,最终通过对目标威胁度的比较,将敌作战意图分为对我具有摧毁性的一类和不具有摧毁性的一类;训练样本的所有目标构成论域U={x1,x2,…,x8};目标的属性构成该系统的条件属性集C={v,h,r,e},其中,v代表目标的飞行速度,速度越快威胁越大;h代表目标的飞行高度,高度越低威胁越大;r代表目标的航路捷径,航路捷径越小威胁越大;e代表目标的干扰能力,由强到弱依次为3、2、1,干扰能力越强威胁越大。

目标类型不同,其速度和攻击能力通常会不一样,从而对被保卫对象的威胁程度也不同。可根据威胁程度由大到小将来袭目标分为6类。第一类:核弹载机、战术弹道导弹(TBM);第二类:空地导弹(精确制导导弹)、反辐射导弹(ARM);第三类:巡航导弹、隐身飞机、大型轰炸机;第四类:歼轰机、指挥机、预警机、干扰机;第五类:小型机、直升机、不明机;第六类:假目标、诱饵、侦察机。令威胁度c5为该系统的决策属性,威胁度由强到弱依次为6、5、4、3、2、1。表1是该目标作战意图识别系统的一个训练数据样本。

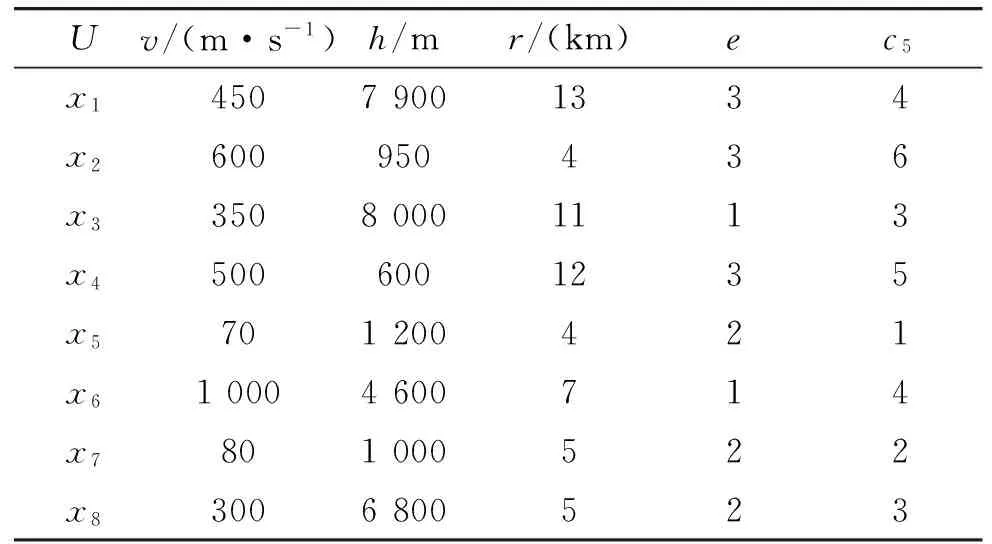
表1 目标作战意图识别系统的训练数据样本

现采用该样本对作战意图识别系统进行训练。由于目标高度及航路捷径均表现出与对保卫对象威胁程度反相关的特性。因此,需要对原始训练样本表进行处理得表2。

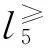
(29)

表2 处理后的训练数据样本

设有新目标,其条件属性值分别是:v=1 200,h=1 000,r=6,e=3,与以上规则不匹配,故不能确定该目标是否具有摧毁性意图。

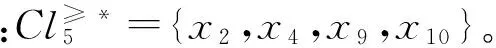
则该双向S-优势集的下近似为:

则导出确定性规则为:

r1:c1≥600∧c2≤950∧c3≤4∧c4≥3→

(30)

r2:c1≥1 100∧c2≤3 000∧c3≤6∧c4≥2→

(31)

若仍对条件属性为:v=1 200 m/s,h=1 000 m,r=6 km,e=3的目标进行判断,此时该目标与规则r2匹配,此时则可以确定该目标具有摧毁性意图。

5 总结

在粗糙集的基础上,考虑集合中元素之间优势关系的同时也考虑到元素的动态迁移特性,提出了双向S-优势粗集。该模型为具有优势关系的信息系统下获得动态决策规则奠定了理论基础。双向S-优势粗集是对粗糙集和双向S-粗集理论的完善和发展。

文章最后在作战意图识别系统领域中对文中提出的双向S-优势粗集进行了应用。通过实验验证了文中提出的双向S-优势粗集模型可以对具有动态特性的偏好信息系统进行有效的处理。

[1] PAWLAK Z. Rough Sets: Theoretical aspects of reasoning about data [M]. Norwell: Kluwer Academic Publishers, 1992.

[2] GRECO S, MATARAZZO B, SLOWINSKI R, et al. An Algorithm for Induction of Decision Rules Consistent with the Dominance Principle [C]∥Rough Sets and Current Trends in Computing, Second International Conference, Rsctc Banff, Canada, October 16-19, 2000, Revised Papers. 2000: 304-313.

[3] 张文修. 粗糙集理论与方法 [M]. 北京: 科学出版社, 2001: 3-22.

[4] INUIGUCHI M, YOSHIOKA Y, KUSUNOKI Y. Variable-precision dominance-based rough set approach and attribute reduction [J]. International Journal of Approximate Reasoning, 2009, 50(8): 1199-1214.

[5] QIAN Y, LIANG J, YAO Y, et al. MGRS: A multi-granulation rough set [J]. Information Sciences, 2010, 180(6): 949-970.

[6] SHI Kaiquan. Two direction S-rough sets [J]. International Journal of Fuzzy Mathematics, 2005, 13(2): 335-349.

[7] SHI K. S-rough sets and knowledge separation [J]. Journal of Systems Engineering and Electronics, 2005, 16(2): 403-410.

[8] 史开泉, 崔玉泉. S-粗集与粗决策 [M]. 北京: 科学出版社, 2008: 12-34.

[9] LEUNG Y, LI D. Maximal consistent block technique for rule acquisition in incomplete information systems [J]. Information Sciences, 2003, 153(1): 85-106.

[10] 骆公志, 黄卫东. 不完备信息系统中的确定优势粗糙决策规则提取 [J]. 南京邮电大学学报(自然科学版), 2011, 31(5): 114-120.

[11] LUO Gongzhi, YANG Xiaojiang, ZHOU Dequn. Rough analysis model of multi-attribute decision making based on limited extended dominance relation [J]. Journal of Systems and Management, 2009, 18(4): 391-396.

[12] SCHNIDT C F, SRIDHARAN N S, GOODSON J L. The plan recognition problem: An intersection of psychology and artificial intelligence [J]. Artificial Intelligence, 1978, 11(1): 45-83.

[13] MULDER F, VOORBRAAK F. A formal description of tactical plan recognition [J]. Information Fusion, 2003, 4(1): 47-61.

[14] SHUN G E, XIA X Z. DSBN used for recognition of tactical intention [J]. Systems Engineering & Electronics, 2014, 36(1): 76-83.

[15] DENG H J, YIN Q J, Ji-Wen H U, et al. Tactical intention recognition based on multi-entity Bayesian network [J]. Systems Engineering & Electronics, 2010, 32(11): 2374-2379.

Two-directionS-dominanceRoughSetsandItsApplicationinIntentionRecognition

ZHANG Xin, LI Xuwu, LU Yanli

(Air and Missile Defence College, Air Force Engineering University, Xi’an 710051, China)

Considering the dynamic of the information system and classic rough sets can’t applied in it. The model of two-direction S-dominance rough sets is proposed. First, the dominance relation and the model of two-direction S-rough sets are combined and the approximation operators of the model are defined. Then, based on the model of two-direction S-dominance rough sets, the properties of the rough approximation operators and the relation between the model and the others are studied. Finally, the model is applied in the issue of intention recognition.

dominance rough sets; two-direction S-rough sets; two-direction S-dominance rough sets; intention recognition

TP18

A

2016-06-03

国家自然科学基金(61272011)资助

张鑫(1992-),男,内蒙古巴彦淖尔人,硕士研究生,研究方向:粗糙集与人工智能。