小视场条件下武器分离影像测量技术*

张建花

(中国飞行试验研究院测试所, 西安 710089)

小视场条件下武器分离影像测量技术*

张建花

(中国飞行试验研究院测试所, 西安 710089)

针对某型飞机上高速摄像机安装位置受限,安装在不同位置的摄像机画面不能重叠,无法采用常规影像测量交会方法计算武器分离过程的轨迹、姿态运动参数的问题,提出多视角非交叠影像测量方法。通过增加刚体目标上标志点之间相对空间关系不变约束条件,使得秩亏影像测量方程组达到满秩条件,实现了武器运动参数的测量。实验结果表明,轨迹测量精度可达到2 cm,姿态测量精度可达到0.6°,满足飞行试验测试要求。

飞行试验;武器分离;非交叠视场影像测量;轨迹;姿态

0 引言

武器离梁段轨迹、姿态、速度、角速度等外部参数是评价武器性能的重要技术指标,是武器试验中的重要测试内容。通常在飞机上加装高速摄像机获取武器高速运动的图像,对图像进行分析得出武器运动参数。

高速摄像机安装位置理想时,可以拍摄到武器的整体外形,测量标志可在视场内分布开,采用单摄像机测量或者双摄像机交会测量都能获得较好的测量结果。但有时由于安装位置受限,摄像机视角比较差,武器挂载在弹架上时,摄像机画面只能看到弹上的局部位置,利用局部范围的影像估算武器的整体运动参数,由于基线太短,测量精度难以提高甚至出现无解的情况。文中针对小视场非交叠条件下的武器分离测试,提出多视角非交叠影像测量方法,实现了武器运动参数的精确测量。

1 测量原理

1.1 测量系统组成

武器分离影像测量系统主要由高速摄像机、触发调节器、时码分配器组成。高速摄像机采用千兆网进行数据传输,在分辨率为1 690像素×1 710像素,采样率500 fps下可记录7 s的数据;触发调节器,以武器发射信号作为输入,经过信号隔离、驱动增强后控制多台高速摄像机的同步拍摄。时码分配器接收飞机上的时码发生器输出的时间信息分配给系统内各摄像机,达到时间统一。

1.2 坐标系建立

根据测试任务书要求,主要关注机弹分离过程中导弹相对于飞机的轨迹和姿态。主要涉及到以下几个坐标系:①飞机坐标系:采用三维直角坐标系,原点O在飞机最前端,Y轴与飞机轴线平行指向机尾,X轴指向飞机的左侧,Z轴垂直YX平面指向上方,构成右手坐标系。②弹体坐标系:

以弹体的质心D为原点,

Xm轴为导弹对称轴并指向弹头,Zm轴垂直指向安装面,Ym轴与ZmXm平面构成右手系。使用全站仪弹体上测量标志点的三维坐标,并将其转换到弹体坐标下。③摄像机坐标系:以摄影中心S为原点,x、y轴与像平面上所选定的x、y轴平行,z轴与摄影方向SO重合,构成右手直角坐标系。

1.3 像机标校

对高速摄像机内外方位元素进行分步检校。摄像机装机前在实验室标校内参数,得到摄像机的焦距f、像主点坐标(x0,y0)、镜头的畸变参数(K1,K2,K3,P1,P2,B1,B2)[1]。待摄像机装机固定后,通过摄影测量的单像空间后方交会原理[2],计算拍摄时刻摄像机的外方位参数(XS,YS,ZS,a1,a2,…,c2,c3)。

1.4 多视角非交叠影像测量方法

由于导弹可以作为刚体[3]对待,虽然各个摄像机的视场互相之间独立,但是刚体的弹体使得各个视场之间又存在着联系,即各个区域测量标志之间的相对空间关系固定不变。因此,可以在各独立视场内的测量标志之间建立关联,从而实现无交叠关系的不同视场的摄像机联合计算。假设摄像机拍摄到两个非交叠视场非交叠区域A和B,如图1所示。

根据摄影测量中像点、摄影中心点以及物方点共线原理[2],可列出A区的条件方程为:

(1)

同理,B区的条件方程为:

(2)

(x01,y01,f1)和(x02,y02,f2)为两台摄像机的内参数;(Δx1,Δy1)和(Δx2,Δy2)是两台摄像机镜头畸变改正;(XSA,YSA,ZSA,a1,a2,…,c2,c3)和(XSB,YSB,ZSB,A1,A2,…,C2,C3)为两台摄像机的外方位参数。通过1.3所述方法得到。另外,(x1,y1)和(x2,y2)分别为两台摄像机视场内测量标志的像点坐标,通过图像判读可得到。(X,Y,Z)则为要求解的测量标志在飞机坐标系下的坐标。

因为刚体的弹体上测量标志点之间相对关系不变,所以测量标志之间有如下的关系:

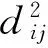
1.5 测量标志布设

在弹体的测量标志布设时,为了使每台摄像机可以看到3个以上测量标志,用于非交叠影像的测量计算,特在弹上的9个截面均匀布设4个测量标志,如图1所示。这样在同一个像机的视场内至少能看到3个以上标志点,因此可以实现此算法。

1.6 姿态数据解算

测量标志点在弹体坐标系中的坐标值在武器试验之前已测定,用(Xmi,Ymi,Zmi)表示;(Xi,Yi,Zi)为标志点在飞机坐标系下的坐标,两个坐标系之间的转换关系可表示为:

(3)

式中：ΔX、ΔY、ΔZ和φ、ω、κ就是要求的轨迹和姿态参数。

1.7 速度解算

由以上方法可以得到武器的轨迹、姿态运动参数,速度和角速度则是通过对轨迹和姿态数据进行微分得到的。由于武器的运动速度极快,高速摄像机的采样时间很短,使得直接通过对时间微分的测量结果对测量误差非常敏感,数据起伏很大。为此通过对测量数据进行Kalman滤波,以提高速度与角速度的精度。

2 试验结果及分析

通过武器投放地面仿真试验,将地面某坐标系假设为飞机坐标系,应用文中提出的非交叠影像测量方法得到了武器相对于地面坐标系的轨迹参数和姿态参数,某次试验的数据曲线如图2所示。

在地面上摄像机视场内布设固定不动的点作为参考点,用全站仪测量其坐标值,通过上述方法计算得到固定点的坐标值,比对测量值和计算值,最大误差是2 cm。根据误差传播理论,可估算出姿态误差为0.6°,满足飞行试验测试要求,可在飞行试验中应用。

3 结束语

文中通过增加刚体目标空间约束条件,实现了对不重叠影像的计算,解决了狭小空间内武器分离过程精确测量的难题。后续,对某型武器进行了多个架次投放试验,完成了武器分离过程中图像获取、轨迹、速度、姿态等参数的解算。相关参数是弹厂改进武器设计的主要依据,促进了新型武器的尽快研制,缩短了科研试飞时间。

[1] 张建花, 柳琦, 聂荣华. 机载影像测量消抖技术研究 [J]. 弹箭与制导学报, 2016, 36(1): 174-176.

[2] 冯文灏. 近景摄影测量 [M]. 武汉: 武汉大学出版社, 2002: 13-14, 123.

[3] 贾浩正, 罗耀蓉. 单影像运动目标六维参数测量方法 [J]. 光电工程, 2010, 37(6): 11-15.

[4] 张建花, 吕鹏涛, 邹强. 机载摄像机快速标定技术研究 [J]. 计算机测量与控制, 2016, 24(2): 166-167.

[5] 黄桂平. 数字近景工业摄影测量关键技术研究与应用 [D]. 天津: 天津大学, 2005.

[6] 武汉大学测绘学院测量平差学科组编.误差理论与测量平差基础 [M]. 3版. 武汉: 武汉大学出版社, 2014.

[7] 王永强. 基于约束算法的大尺寸三维视觉测量方法研究 [D]. 北京: 北京邮电大学, 2006.

ImageMeasurementTechnologyofWeaponSeparateinSmallField

ZHANG Jianhua

(Test Institute, China Flight Test Establishment, Xi’an 710089, China)

The high-speed cameras installated on a certain type of aircraft are limited, the field of cameras cannot overlap, so the routine intersection measurement method cannot be used. For this problem, the paper presents a multi-view un-overlap image measurement method. Through adding the constraint of relative spatial relations invariant between two marks on rigid object, the rank-defect image measurement equation set can reach full rank condition and then achieve the measurement of weapons separate moving parameters. The experimental results show that the accuracy of track measurement can achieve 2 cm and attitude measurement can achieve 0.6°, and which meet the fight test requirement.

fight test; weapon separate; un-overlap image measurement; track; attitude

PT391

A

2016-03-06

张建花(1983-),女,陕西商洛人,工程师,硕士,研究方向:飞行试验光电测试、影像测量、数字图像处理技术。