基于系统辨识的冲压发动机动态模型分析*

梁俊龙, 张贵田, 胡宝文

(1 西北工业大学固体火箭发动机燃烧、热结构与内流场国防科技重点实验室, 西安 710072;2 西北工业大学航天学院, 西安 710072)

基于系统辨识的冲压发动机动态模型分析*

梁俊龙1, 张贵田1, 胡宝文2

(1 西北工业大学固体火箭发动机燃烧、热结构与内流场国防科技重点实验室, 西安 710072;2 西北工业大学航天学院, 西安 710072)

冲压发动机动态模型是研究控制系统的基础,动态模型的准确性直接影响控制方案的有效性。为了获得面向控制的高精度低阶动态模型,利用试验数据,理论分析传递函数模型,选择误差平方和最小作为辨识准则,并利用非线性最小二乘法对模型进行辨识,获得了燃油控制系统中燃油流量对燃油指令的传递函数模型。进而将该模型和发动机气路通道模型结合起来,建立了发动机推力对燃油流量的传递函数模型。辨识模型的时域特性曲线与试验数据符合得很好,能够代表发动机系统的主要动态特性。

冲压发动机;动态模型;燃油控制系统;传递函数;参数辨识

0 引言

液体冲压发动机作为超声速巡航导弹武器和飞行器的理想推进系统[1],与飞行器耦合较强[1-2],其推力调节过程对弹道优化至关重要[3]。冲压发动机动态模型的建立是发动机控制系统设计与性能分析的基础[4],动态模型的准确性决定了控制规律设计、控制系统仿真的有效性,直接影响飞行器控制系统方案设计和弹道优化。建立有效的低阶动态特性模型有利于降低控制系统的设计难度,提高仿真效率,降低控制系统的风险,减小研制成本[4]。

建立发动机数学模型主要有理论建模和系统辨识两种基本方法。冲压发动机动态特性理论建模研究主要包括基于分布参数的小偏差线性化方法[5-7]和基于集中参数的小偏差线性化方法[8],前者能够考虑进气道、燃烧室、尾喷管组成的气路通道的沿程压力、推力等对燃油流量的响应特性,而后者忽略了冲压发动机气流通道内的燃烧、激波运动、压力波传播等过程的动态特性,仅考虑执行机构的动态特性。系统辨识方面,主要是基于CFD数值计算结果[9-10]和试验数据的系统辨识方法[11-13]。基于数值仿真结果的辨识方法其精确性依赖于数值计算结果的有效性。而基于试验数据的方法能够有效的利用试验数据得到合理的模型并与试验数据符合得很好,准确度较高。

冲压发动机燃油流量控制的数学模型主要有线性模型和非线性模型。非线性动态特性研究[14-19]多利用液压仿真软件,对系统的动态特性进行非线性建模和仿真分析,计算量较大,对控制系统设计和仿真分析带来了很大的困难。线性模型主要是基于各部

件小偏差线性化方法而建立[20-22],计算量小,但适应范围有限。

文中主要基于系统辨识原理和方法,利用冲压发动机试验数据,根据发动机的工作特点,考虑了燃油调节与控制过程和发动机的推力建立过程的工作特性,建立燃油控制系统和发动机推力对燃油流量的传递函数模型,并以低阶有理多项式传递函数的方式给出,为冲压发动机控制系统设计、仿真和分析奠定基础。

1 系统辨识原理

系统辨识就是在输入和输出的基础上,由规定的一类系统模型中确定一个系统模型,使之与被测系统等价。系统辨识包含三大要素:系统的输入输出数据、模型类和等价准则。系统辨识的目的就是根据系统的测量信息,在某种准则意义下,估计出模型的未知参数,其基本原理见图1。

为了得到模型参数θ的估计值,通常采用逐步逼近的办法。在k时刻,根据前一时刻的估计参数计算出模型该时刻的输出,即系统输出的预报值:

(1)

同时计算出预报误差:

(2)

因此,系统输出量:

z(k)=hT(k)θ0(k-1)+e(k)

(3)

等价准则是系统辨识问题中不可缺少的要素之一,它用来衡量模型接近实际过程的准则,通常表示为一个误差的泛函,因此,等价准则也叫误差准则,记作:

(4)

式中f(·)是ε(k)的函数。用的最多的是平方函数,即:

f(ε(k))=ε2(k)

(5)

ε(k)是定义在区间(0,L)上的误差函数。这个误差函数应该广义的理解为模型与实际过程的“误差”。输出误差在辨识中是应用最广泛的一种误差准则,如图2所示。实际系统和模型的输出分别记作z(k)和zm(k)时,则实际输出与模型输出的偏差称为输出误差如式(6)所示。

ε(k)=z(k)-zm(k)

(6)

若误差最小,则模型与实际系统符合得最好。为了获得最优的模型参数,通常采用非线性优化算法获得误差平方和最小的模型参数。为了便于评价辨识模型与实际系统的匹配程度,选择误差均方根作为指标,即:

(7)

文中研究的冲压发动机由气流通道和燃油控制系统组成,气流通道是指进气道、燃烧室、尾喷管构成的气流流动系统。推力调节过程主要包括燃油控制系统根据燃油设定值对燃油流量的调节过程和气流通道根据燃油流量的变化引起推力变化的过程。为了建立燃油设定值阶跃变化时,推力对燃油流量设定值的动态特性模型必须建立燃油控制系统和气流通道的模型,发动机全系统的数学模型如下:

Gt(s)=Gf(s)Gg(s)

(8)

式中:Gt(s)是发动机全系统模型;Gf(s)是燃油控制系统的模型;Gg(s)是气流通道的模型。

2 燃油控制系统的动态特性分析

冲压发动机的燃油控制系统主要包括综合控制器和燃油调节器。燃油调节器结构复杂,运动部件多,导致燃油调节器的非线性较强。为了获得适应范围较宽且准确可靠的动态特性模型,将燃油控制器和调节器作为整体,对其动态特性进行辨识。

根据系统辨识原理,输入信号u是阶跃变化的燃油流量设定值,试验中燃油控制系统输出的燃油流量测量值z与辨识模型预测的燃油流量zm的偏差是输出信号。

首先,根据理论分析和控制系统需求,选择模型类,以式(7)定义的误差均方根作为误差准则,以误差最小为目标,利用非线性最小二乘问题的求解方法进行参数辨识获得理论模型的参数,从而建立燃油控制系统的动态特性模型。

2.1 模型类的选择

根据燃油调节器计量阀的动态特性的理论分析,该环节可以用一阶环节近似[22],为比例环节、惯性环节和延迟环节的串联。

(9)

由于燃油控制器采用了PID控制方法,忽略占空比信号的饱和特性,整个燃油调节控制系统的闭环传递函数至少是二阶的,因此,在辨识模型类的选择中,选择二阶环节。

燃油控制系统的试验数据中包含燃油流量的反馈值和设定值,燃油流量的设定值按照阶跃特性变化。燃油流量的阶跃响应存在明显的超调和纯延迟,这个特性用欠阻尼二阶环节加纯延迟环节描述,虽然辨识模型的阶次越高能包含的环节越多,但是复杂度大大增加,且增加了控制系统设计的难度,因而,以阶数最少且能描述燃油控制系统的主要特性为原则,选择实际燃油流量对燃油流量设定值的传递函数的形式为:

(10)

式中:τ为纯延迟时间;参数k、a、b、c为常数,纯延迟时间和模型中的常数通过参数辨识获得。

2.2 参数辨识

当模型类确定后,系统辨识的下一步就是参数辨识。为了使得各组试验具有可比性,对试验数据进行归一化,将试验数据转换为标准阶跃响应特性,这种处理方法可以用下式表示:

(11)

式中:y0是试验数据y的起始阶段的平均值;y1是试验数据y的稳定阶段的平均值;t0是阶跃变化的起始时刻。

参数辨识中,等价准则选择为输出误差准则,最优的参数是指这组参数下,模型的阶跃响应与试验数据的误差的平方和最小,该方程的求解等效于非线性最小二乘问题,可利用Matlab的非线性曲线拟合函数来完成参数的辨识,通过计算得到辨识模型为:

(12)

辨识模型与第3次试验中的3组阶跃响应数组的偏差依次为0.06、0.06和0.07,与模型1相比,拟合误差降低了一个数量级,拟合效果更好。模型对燃油流量的预测结果与测量的燃油流量的对比如图3所示,预测结果与3组曲线的峰值时间、峰值、调节时间等吻合得较好,可以用式(12)表示的辨识模型来描述流量变化范围较大时燃油流量控制系统的动态特性。这也说明文中选择的模型类具有很好的通用性,能够在一定范围内对不同状态点的动态特性进行描述,也能用于其他状态点的试验数据的辨识,从而根据辨识模型参数的差异对燃油控制系统的动态特性影响因素进行分析,获得适应范围广的低阶高精度模型,为先进控制算法的应用奠定基础。

3 推力对燃油流量的响应特性分析

气路通道内推力对燃油流量阶跃输入下的响应特性是发动机全系统推力模型的关键特性。首先建立气流通道内推力对燃油流量的动态特性模型,文中采用基于气流通道工作原理的建模方法。对气流通道的一维分布参数模型进行小偏差线性化得到传递矩阵模型。在理论建模和线性化过程中,考虑燃油流量变化引起的推力变化[6]。根据理论模型,获得推力对燃油流量变化的频率特性,再利用频域数据辨识获得高阶传递函数模型,对高阶高精度模型进行模型降阶获得低阶模型[6]。气流通道内压力对燃油流量的响应特性[2]可以用式(13)来表示。

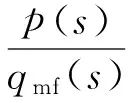
(13)

式(13)表示发动机气流通道内部某一点的气流压力对供油量变化的动态响应。其中K表示对供油量变化敏感程度的参数,是静态参数;p(s)为发动机内部某截面压力的拉普拉斯变换,s为拉普拉斯算子;qmf(s)为发动机燃油流量的拉普拉斯算子;e-τs表示由发动机供油至产生压力变化之间的延迟特性,τ为延迟时间;T为时间常数;σ为跃升比。

气流通道内进气道、燃烧室和尾喷管的参数是互相影响的,只有全部稳定后,整个气流通道才稳定,而推力是由气流通道内部的压力分布特性确定的,因而,气流通道内推力对燃油流量的传递函数与压力对燃油流量的传递函数相同,则推力对燃油流动的模型类为:

(14)

这些参数根据发动机的来流气体和燃油流量利用文献[6]的方法进行理论计算获得。因此,根据式(8),发动机全系统中推力对燃油流量设定值的传递函数模型为:

(15)

冲压发动机的推力与高速来流相关,测量推力很困难,因而,无法直接用实测推力数据进行验证,合适的方法是选择燃烧室压力进行间接验证。试验过程中,燃油控制系统和发动机气流通道是相互作用的,试验测量的燃烧室压力是全系统动态特性的体现,将全系统模型的动态特性与试验数据进行对比来验证系统模型的正确性。对于某次发动机整机试验,发动机的传递函数为:

(16)

这个模型与该次联合动力试验中室压的偏差为0.13和0.15,时域特性对比如图4所示。该次试验中两组阶跃响应数据与理论模型的趋势和平均值吻合得较好,可以用辨识模型来表示冲压发动机的动态特性。该模型类阶次较低,却能够反映发动机的主要动态特性,低阶模型便于控制系统设计和仿真。这种建模方法具有通用性,可用于发动机其他工况的动态特性建模,以获得不同工作点的模型,进而获得适应范围广的通用模型或者具有高精度的分段模型,为鲁棒控制、自适应控制等控制方法在冲压发动机上的应用奠定基础。

4 结论

根据液体亚燃冲压发动机的工作过程,利用系统辨识原理和方法对试验数据进行分析,建立了燃油控制系统和发动机推力对燃油流量的传递函数模型,得到如下结论:

1)利用发动机试验数据,利用系统辨识方法,获得了燃油控制系统中,实际燃油流量对燃油流量设定值的传递函数模型,该模型能够很好的描述燃油控制系统的动态特性,并且该模型类具有通用性,可以用作其他工况点的模型类,通过对不同工况点的建模为先进控制算法的应用奠定基础。

2)利用燃烧室压力测量数据,对发动机全系统推力对燃油流量设定值的传递函数模型进行了辨识,结果表明辨识模型的时域特性与试验数据符合得较好。

3)冲压发动机燃油控制系统和气流通道建模方法具有通用性,可以用于获得不同工作点的动态特性模型,该辨识动态模型可用于控制系统设计、仿真和控制参数优化。

[1] 马杰, 梁俊龙. 液体冲压发动机技术发展趋势和方向 [J]. 火箭推进, 2011, 37(4): 12-17.

[2] 龚春林, 谷良贤, 袁建平. 飞航导弹基于响应面近似技术的并行子空间优化设计 [J]. 西北工业大学学报, 2005, 22(3): 393-395.

[3] 刘恒军, 沙建科, 王华. 冲压发动机导弹弹道多目标优化 [J]. 系统仿真学报, 2009, 21(9): 2764-2766.

[4] 谢光华, 孟丽, 薛恩, 等. 液体冲压发动机控制系统半实物仿真 [J]. 推进技术, 2001, 22(6): 451-453.

[5] 刘华, 雍雪君, 梁俊龙, 等. 超声速进气道及冲压发动机动态特性分析 [J]. 火箭推进, 2013, 38(3): 17-22.

[6] QIN Yanping, LIANG Junlong, LI Bin, et al. Investigation of ramjet engine dynamics based on genetic algorithm [C]∥ 14th International Space Conference of Pacific-basin Societies.[S.l.:s.n.]， 2014.

[7] 张宏, 陈玉春, 蔡大虎, 等. 液体冲压发动机仿真模型研究 [J]. 计算机仿真, 2008, 25(7): 70-72.

[8] 聂玲聪, 朴胜志, 吴智锋，等. 几何可调液体冲压发动机多变量控制算法研究 [J]. 推进技术， 2013， 34(12): 1690-1695.

[9] GUPTA N K, GUPTA B K, ANANTHKRISHNAN N, et al. Integrated modeling and simulation of an air-breathing combustion system dynamics: AIAA 2007-6374 [R].[S.l.:s.n.], 2007.

[10] KUMAR P B C, GUPTA N K, ANANTHKRISHNAN N, et al. Modeling, dynamic simulation, and controller design for an air-breathing combustion system: AIAA 2009-708 [R].[S.l.:s.n.], 2009.

[11] 郭迎清, 王海泉. 涡扇发动机模型辨识及其控制器设计 [J]. 现代制造工程, 2006(9): 73-75.

[12] 李辉, 俞进, 李淑英, 等. 基于支持向量机的燃气轮机启动过程建模 [J]. 燃气轮机技术, 2012, 25(1): 48-51.

[13] 梅晓川. 基于改进BP网络的航空发动机起动过程辨识 [J]. 航空计算技术, 2009, 39(6): 58-61.

[14] 王昕. 流量调节器动态特性研究 [J]. 火箭推进, 2004, 30(3): 19-24.

[15] 李吉. X6发动机燃油调节器建模与仿真研究 [D]. 西安: 西北工业大学, 2006.

[16] 冯海峰, 樊丁. 某型航空涡轴发动机燃油调节器建模与仿真 [J]. 计算机仿真, 2007, 24(12): 45-48.

[17] 何远令, 龚建政, 石恒, 等. 燃气轮机燃油调节器的建模与仿真研究 [J]. 舰船电子工程, 2009, 29(12): 145-148.

[18] 林峰, 马静, 王镛根. 基于VC++. Net与Matlab的燃油调节器仿真 [J]. 计算机仿真, 2005, 22(12): 41-44.

[19] 尤裕荣, 赵双龙, 吴宝元, 等. 基于AMESim的冲压发动机燃油调节器动态特性仿真 [J]. 火箭推进, 2010, 36(4): 13-15.

[20] 马静, 王镛根. 某型导弹燃油调节器的建模及仿真研究 [J]. 计算机仿真, 2003, 20(9): 36-38.

[21] 马静, 王镛根. 某型燃油调节器的建模及仿真研究 [J]. 液压气动与密封, 2002(5): 13-15.

[22] 秦艳平, 李斌, 梁俊龙, 等. 面向控制的燃油调节器动态特性研究 [J]. 火箭推进, 2012, 18(5): 7-12.

DynamicCharacteristicModelAnalysisofRamjetEngineBasedontheSystemIdentificationMethod

LIANG Junlong1, ZHANG Guitian1, HU Baowen2

(1 National Key Laboratory of Combustion Flow and Thermo-structure, Northwestern Polytechnical University, Xi’an 710072, China; 2 School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The dynamic model of ramjet is fundamental for control system of ramjet. Furthermore, the accuracy of dynamic model directly impacts the viability of control scheme. In order to get control-oriented high accuracy dynamic model with low order, according to the test results, the transfer function model of the theoretical analysis, select the minimum error sum of squares as the system identification criterion, and to identify the model by using nonlinear least squares method, the transfer function model of fuel flow in fuel control system is generated. By combining this model with the engine air path model, the transfer function model of the engine thrust to the fuel flow is established. The time domain characteristic curve of the identification model is in good agreement with the test results, which can represent the main dynamic characteristics of the engine system.

ramjet engine; dynamic model; fuel control system; transfer function; system identification

V235.213

A

2016-07-20

梁俊龙(1977-),男,河南桐柏人,研究员,博士研究生,研究方向:航空宇航推进理论与工程。