基于时频图像纹理特征的雷达辐射源信号识别*
2017-11-01孟凡杰王义哲刘俊杰
孟凡杰, 唐 宏, 王义哲, 刘俊杰
(空军工程大学防空反导学院, 西安 710051)
基于时频图像纹理特征的雷达辐射源信号识别*
孟凡杰, 唐 宏, 王义哲, 刘俊杰
(空军工程大学防空反导学院, 西安 710051)
为了解决低信噪比条件下雷达辐射源信号识别率低的问题,提出了一种提取时频图像纹理特征的脉内调制方式识别方法。该算法首先对信号进行Choi-Williams变换,在对时频图进行预处理后提取其改进的局部二值模式纹理特征(LBPV),并用支持向量机进行分类判别。使用6种典型雷达信号进行仿真实验,仿真结果表明在-2 dB的低信噪比条件下该方法的平均识别率可达95%以上,局部二值模式算子在低信噪比下的识别能力得到大的提高。
雷达辐射源信号识别;Choi-Williams分布;局部二值模式;纹理特征
0 引言
雷达辐射源信号识别是电子侦察和对抗领域的重要内容。脉内调制特征可以有效拓展信号识别的参数空间,有助于降低特征交叠概率,使复杂体制雷达信号的识别成为可能,因而成为雷达辐射源信号识别领域的重要研究方向。时频分析法是研究脉内调制特征的重要方法,它突破了单时域分析和单频域分析的局限性,能够以时频分布图的形式刻画信号的实时频率特征。近年来,许多学者利用图像处理技术从时频分布图中提取脉内调制特征,并取得了一些成果[1-3]。文献[1]利用主分量分析法提取时频图像的代数特征,在中等以上信噪比时取得了较好的识别效果,但在低信噪比条件下识别效果不太理想。文献[2]提取灰度图像的伪Zernike矩阵特征进行识别,分类器结构简单,抗噪能力强,但其对相位编码信号的识别率仍有待提高。文献[3]利用图像处理的方法实现对多种LPI雷达信号的准确识别,但亦存在数据维数高、计算量大的问题。
纹理特征可以反映图像的灰度统计信息和空间结构分布信息,具有良好的抗噪性和鲁棒性,是图像识别领域的重要研究方向。局部二值模式(LBP)算法是一种常用的纹理特征提取方法。该算法首先提取图像的局部空间模式,再通过统计分析作整体的特征提取,具有尺度不变性、旋转不变性和运算速度快等优点。但传统的LBP算法只关注图像局部灰度差,忽略了对比度信息,对图像纹理特征的描述是不充分的[4]。
文中首先利用Choi-Williams变换得到6种典型雷达辐射源信号的时频分布图,再利用改进的局部二值模式算法(LBPV)提取包含在时频分布图中的信号脉内调制特征。由于支持向量机分类器结构简单、泛化能力强,在解决小样本、非线性以及高维特征识别问题时具有独特优势,文中采用支持向量机实现最终的分类识别。
1 时频图获取
雷达辐射源信号是非平稳信号,时频分析方法则是处理非平稳信号的重要方法。Wigner-Ville分布是当前广泛使用的一种时频分布。信号s(t)的Wigner-Ville分布定义为:
(1)
Wigner-Ville分布中会不可避免地出现交叉干扰项,在实际运用中往往对其进行改进[5]。
Cohen类时频分布是将Wigner-Ville分布与一个二维平滑函数φ(τ,v)卷积,φ(τ,v)是核函数,决定了干扰项抑制的效果。Cohen类时频分布可表示为:
φ(τ,v)e-j2π(vt+τf-uv)dudτdv
(2)
在Cohen类时频分析表达式中,如果取核函数为指数函数,即:
φ(τ,v)=e-τ2v2/σ
(3)
则可得到Choi-Williams分布,即:
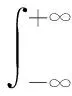
(4)
式中:σ(σ>0)是缩放因子,它的大小与交叉项幅值成正比例关系。选择合适的σ可以有效的抑制交叉干扰项,同时又较少的牺牲时频聚集性。研究表明,在[0.1 10]之间选择σ比较合适[6],文中选定σ=1。作为Wigner-Ville分布的加窗平滑定义,Choi-Williams分布具有良好的交叉干扰项抑制效果,具备较好的抗噪能力,是一种有效的高分辨时频分析方法。图1是6种典型雷达辐射源信号在信噪比为5 dB时的Choi-Williams时频分布图。Choi-Williams分布时频图直观反映了信号的脉内调制信息,因而可以利用图像处理方法从中提取信号脉内调制特征。
2 LBPV算子
LBP是一种简单高效的纹理特征描述算法,其主要思想是将局部图像中心像素点与其邻域内其他像素点灰度值的差异模式化,并通过统计各种模式出现的频次规律来描述图像中所包含的纹理信息。由于LBP及其改进算法具有运算量小、对旋转、光照不敏感等特点,因此在人脸识别、医学图像检测和工业视觉检测等领域广泛应用。
如图2所示,定义灰度图的局部窗口为一个半径为R、邻域点数为P的圆环形区域(图中R=2.5,P=12),中心像素点在圆心位置,坐标为(a,b),灰度值用gc表示。邻域内P个邻域点均匀分布于圆周,坐标为(a+Rcos(2πi/P),b+Rsin(2πi/P)),灰度值用gi(i=0,…,P-1)表示,当邻域点不是位于整数坐标位置时,用双线性内插法计算其灰度值。以gc为阈值,将邻域点的像素值二值化。当邻域点灰度值小于gc时将该点赋值为0,当大于或等于gc时则赋值为1。然后根据邻域点的位置不同进行加权求和,便可得到该局部邻域窗口的LBP值。即:
(5)
当图像旋转时,由于邻域点沿着圆周移动导致LBP模式可能会发生变化(全0或全1时不变),因此Timo Ojala等提出旋不变LBP[7]:
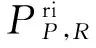
(6)
式中:ROR(x,i)代表旋转函数,表示将x向右旋转i(|i| (7) 式中: U(LBPP,R)=|s(gP-1-gc)-s(g0-gc)|+ (8) uniform模式指的是所有LBP二值序列中至多包含两个从0到1或从1到0跳变的模式,在全部2P种LBP模式中,共有P(P-1)+3属于均匀模式。当圆域半径为2.5、采样点数为12时,uniform模式可以将LBP算子个数由原先的256种减少至135种,具有旋转不变性的uniform模式LBP个数则可进一步减少至14种。尽管类别数量占比不高,但其出现概率却占所有模式的90%以上。因此uniform模式相对普通LBP而言不仅大大减少了特征维数,而且仍能较好保留其局部纹理特性,使高效准确的机器自动识别成为可能。 尽管LBP算子具有很多优点,但由于LBP算子仅描述局部纹理的空间结构,不考虑图像对比度信息,每种LBP模式无论其灰度值大小在统计直方图时都具有相同的权重,因此对图像纹理特征的描述是不充分的,对于模式相同,灰度强度不同的LBP模式可能会出现大量错分的现象。 方差VARP,R可以描述图像的对比度信息,同时也具有旋转不变性的优点,可以和LBP算子实现特征互补,提高分类的准确率。以gc为中心的局部方差可定义为: (9) 式中: (10) 当考虑对比度信息时,通常利用LBP与VAR的联合算子(LBPP,R/VARP,R)对图像纹理特征进行描述。VAR是一个连续值,转换成识别特征时必须进行量化处理,量化过程的阈值选择十分依赖样本,量化过程难以把握,容易产生比较大的量化误差,而且联合算子的特征维数大,影响分类效率。因此文中引入LBPV算子[3]用于时频图像纹理特征的识别。LBPV算子改进了传统LBP直方图中各LBP模式等权值的缺陷,将VAR作为各LBP模式的权值,即: (11) (12) 式中k∈[0,K]。方差表征的是灰度变化的强度,方差较大的局部区域更有利于识别,对识别的贡献更大,因此需要分配比较高的权重值。利用VAR对各LBP模式权值进行再分配避免了VAR的量化过程,减少计算量的同时提高了特征的区分度,因此识别效率优于普通LBP。为验证LBPV的优越性,提取图1中CW、BPSK和LFM 3种信号识别图的圆域旋不变uniform模式,共14种模式,利用普通LBP和LBPV两种不同方法加权后统计其直方图,结果如图3所示。 由图3可知,传统LBP中各模式直方图虽然存在一定差异,但总体来看比较接近,不同信号之间差异较小,不利于后续的识别。与之相反,利用方差加权后的LBPV特征更好地体现了类间差异。基于以上优点,文中采用圆域旋不变uniform模式的LBPV算子作为特征进行时频图像的识别。 3.1 分类器设计 雷达辐射源识别属于小样本、高实时的智能识别,因此文中选用支持向量机(support vector machines,SVM)作为分类器[8]。 SVM是一种建立在统计学习理论基础上的机器学习方法。统计学习理论采用结构风险最小化准则,在实现样本点误差最小化的同时,也可以将结构风险最小化,从而使模型的泛化能力得到提高。使用时灵活、方便,不易陷入局部最小值,且不受数据维数的限制。在解决小样本、非线性、高维数问题时比传统的神经网络方法具有突出的优势。支持向量机分类器性能的发挥与其核函数选择和参数寻优策略紧密相关。由于径向基核函数(RBF)收敛域宽、适用范围广,是较为理想的分类依据函数,因而目前应用最多。在径向基核函数SVM中,主要考虑误差惩罚因子C和核函数方差σ两个参数。参数C主要用来平衡算法复杂度和逼近误差,C越大则对数据的拟合程度越高,但泛化能力降低。σ主要用来控制样本数据在高维特征空间中分布的复杂程度,进而影响运算的效率。因此在进行参数选择时必须同时兼顾C和σ,文中选用网格搜索法[9]对(C,σ)两个参数寻优。 3.2 算法流程 文中算法主要立足于雷达辐射源信号时频变换和时频图像纹理特征的提取和识别,其基本流程如下: 1)对信号进行Choi-Williams变换,并将其转化为灰度图像。 2)利用图像处理技术,对时频灰度图进行裁剪和归一化,为减少噪声的影响,再对图像进行自适应维纳滤波。 3)提取图像的圆域旋不变uniform模式的LBPV算子作为识别特征 4)利用RBF支持向量机对输入的特征进行学习,并进行测试,得到算法的识别率结果。 仿真实验采用6种常规雷达辐射源信号用于分类识别,它们分别是常规脉冲信号(CW),线性调频信号(LFM),二相编码信号(BPSK),四相编码信号(QPSK),频率编码信号(FSK),偶二次调频信号(EQFM)。其中,BPSK采用13位巴克码,QPSK采用16位FRANK码,FSK采用COSTAS码。LFM调频带宽设为5 MHz,信号载频设为20 MHz,采样频率为100 MHz,脉冲宽度为16 μs,噪声为零均值的高斯白噪声。信号的初始相位在0到2π之间随机产生。信噪比设置为从-4 dB到10 dB,每隔两个信噪比产生50个样本,6种信号共计产生2 400个样本信号,每个样本信号依次进行CWD获得其时频分布,利用960个样本用于训练,另外1 440个用于测试。为对比说明LBPV算子识别性能的提高,文中还对LBP算子的识别性能进行仿真分析,并记录了特征提取时间。仿真实验平台为基于联想PC的MATLAB软件,PC机的CPU主频为3.10 GHz,运行内存为4 GB。 表1 LBP和LBPV算法对比 表1是在不同信噪比下LBP和LBPV两种算子的6种信号的平均识别率和平均特征提取时间对比。由图可知,随着信噪比的改善,两种信号都能取得较好的识别效果,但LBPV算子的识别效果明显优于LBP算子,检测性能相对稳定,在-2 dB便可取得平均95%以上的识别概率。当用LBP算子作为识别特征时,各类信号特征差别相对较小,信噪比降低时图像成像质量下降,识别率受此影响显著。由于在提取LBPV特征时需要对每个局部单元重新进行一次赋值,因此计算量稍大于LBP特征,实时性有一定程度的降低。但从仿真结果来看,二者差别不大。融入了方差特征的LBPV算子可以很好的兼顾局部和全局信息,可以提取更加全面的纹理特征用于识别。仿真说明LBPV算子具备良好的抗噪能力,可在较低信噪比条件下完成分选识别。 LFM的时频曲线为一条直线,当调制参数不同时,其时频曲线的变化表现为直线的旋转即斜率的改变。LBP算子具有旋转不变性,对相同调制方式但调制参数不同的信号,尤其是对LFM而言,理论上可能出现错分现象[10]。为考察LBPV算子在这种情况下的识别能力,设置6组LFM信号,其频偏分别为3 MHz、4 MHz、5 MHz、6 MHz、7 MHz、8 MHz,其他参数设置同上。计算机仿真结果如图4所示。 从图4可以看出,LFM参数的改变虽然会使LBPV算子的识别率有一定程度的下降,但总的来看影响不大,正确识别率仍然处于90%以上的高值区间。对于Choi-Williams变换而言,不同调制参数的LFM时频图像不仅斜率不同,直线的时频聚集程度和灰度分布等特征也会发生改变,而融合了局部方差的LBPV算子恰好可以利用这种变化,取得了比较理想的识别效果,因此可以认为LBPV算子不仅可以较好的识别不同调制类型信号,对调制类型形同但参数不同的信号亦可准确识别。 针对低信噪比条件下雷达辐射源信号脉内调制方式的识别问题,文中提出了一种基于LBPV算子的时频图像纹理特征识别方法,该算法从信号的时频图像出发,充分利用灰度图像的纹理特征,实现了利用较少的特征维数取得较好的脉内调制方式识别效果。由LBPV算子构成的分类器结构简单,运算效率高,对辐射源信号参数的变化具备较好的适应能力,具有一定的工程运用研究价值。 [1] GULUM T O. Autonomous non-linear classification of LPI radar signal modulation: ADA 473944 [R]. Monterey: Naval Postgraduate School, 2007. [2] 张立东, 吕涛, 王东风, 等. 一种基于Zernike矩双谱的雷达信号特征提取新算法 [J]. 舰船电子对抗, 2012, 35(6): 43-47. [3] 熊坤来, 罗景青, 吴世龙. 基于时频图像和神经网络的LPI雷达信号调制识别 [J]. 弹箭与制导学报, 2011, 31(5): 230-233. [4] GUO Zhenhua, ZHANG Lei, ZHANG D. Rotation invariant texture classification using LBP variance (LBPV) with global matching [J]. Pattern Recognition, 2010, 43(3): 706-719. [5] 李秀梅, 杨国青, 高广春. 基于LPFT时域滤波器的WVD交叉项抑制方法 [J]. 电路与系统学报, 2013, 18(1): 122-126. [6] PLESSIS M C, OLIVIER J C. Radar transmitter classification using a non-stationary signal classifier [C]// Proceedings of the 2009 International Conference on Wavelet Analysis and Pattern Recognition. Pretoria. South Africa: IEEEPress, 2009: 482-485. [7] OJALA T, PIETIKAINEN M, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987. [8] 张葛祥, 荣海娜, 金炜东. 支持向量机在雷达辐射源信号识别中的应用 [J]. 西南交通大学学报, 2006, 41(1): 25-30. [9] 李琳. 基于RBF核的SVM学习算法优化及其在蛋白质二级结构预测中的应用 [D]. 武汉: 武汉科技大学, 2006. [10] 白航, 赵拥军, 胡德秀. 时频图像局部二值模式特征在雷达分类识别中的应用 [J]. 宇航学报, 2013, 34(1): 139-146. RadarEmitterSignalRecognitionBasedonTextureFeatureofTime-FrequencyImage MENG Fanjie, TANG Hong, WANG Yizhe, LIU Junjie (Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China) To solve the problem of low rate in radar emitter signal recognition under low SNR, a new approach using texture feature of time-frequency image for recognition of intra-pulse modulation is proposed. At first, the time-frequency images of radar emitter signals are obtained by Choi-Williams transform, and then the noise reduction and normalization of these images are processed. After that, the improved arithmetic of LBPV is used to extract the features of time-frequency images. At last, the support vector machine is used for classification and discrimination. In this paper, six kinds of common radar signals are used in simulation experiments. The results show that the average recognition rate can reach 95% when the SNR is as low as -2 dB. radar emitter signal recognition; CWD; LBP; texture features TN974 A 2016-06-07 孟凡杰(1992-),男,河南洛阳人,硕士研究生,研究方向:雷达信号处理。
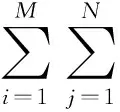
3 分类器设计和算法流程
4 仿真分析

5 结论
