某型炮射导弹膛内运动时期药柱的应力应变分析*

王海清, 隋 欣, 丁娜仁花, 宋长健, 李世鹏, 王宁飞

(1 北京理工大学宇航学院, 北京 100081; 2 天津中德应用技术大学航空航天学院, 天津 300350)

某型炮射导弹膛内运动时期药柱的应力应变分析*

王海清1,2, 隋 欣1, 丁娜仁花2, 宋长健2, 李世鹏1, 王宁飞1

(1 北京理工大学宇航学院, 北京 100081; 2 天津中德应用技术大学航空航天学院, 天津 300350)

炮射导弹发射过程中承受上万个g的过载,固体推进剂药柱的应力应变分析极为关键。文中采用有限元方法对药柱在发射过程中的应力应变进行数值模拟,分别对比研究轴向过载、旋转载荷和药柱-挡药板之间摩擦对药柱整体最大von Mises应力和最大应变变化的影响规律。结果表明,考虑旋转和药柱-挡药板之间摩擦的情况下,药柱整体最大von Mises应力和最大应变都显著增加,而且药柱-挡药板之间摩擦将直接影响药柱最大von Mises应力和最大应变发生的区域。

炮射导弹;固体火箭发动机;推进剂药柱;应力应变分析

0 引言

固体火箭发动机是导弹、炮射导弹的主要动力装置[1]。由于火炮特殊的发射方式,炮射导弹在火炮膛内运动阶段,导弹承受弹底几百兆帕火药燃气压力的推动,轴向过载高达上万个g。因而,抗过载一直是该类固体火箭发动机的研制重点和难点。在固体火箭发动机各分系统中推进剂药柱抗高过载能力最为薄弱,在一定程度上决定着整个发动机的抗高过载能力[1-2]。所以,研究炮射导弹在膛内运动阶段固体推进剂药柱的应力应变分布及其变化规律对于炮射导弹的研究至关重要。

之前的研究工作中,魏卫和王宁飞[2-4]采用数值模拟的方法研究了截面形状、长径比对固体推进剂药柱受到高加速度冲击时发生形变的影响。研究表明,当药柱为厚壁柱壳、星形及圆柱形时,药柱截面形状对发生小变形药柱的应变影响并不显著。轴向形变与长径比成正比关系,并与模量成反比关系。隋欣[5-6]等就某轴向过载6 000g的固体火箭发动机推进剂药柱在发射过程中的应力应变场进行了数值模拟,研究表明,最大等效von Mises应力及应变值均发生在装药底部,装药与支撑面接触面积的变化,会引起装药最大等效应力和最大等效应变的变化,并且就衬垫材料泊松比对于缓和装药内部最大等效应力的影响关系开展研究。唐国金和周建平[7]探讨了用于自由装填药柱应力分析的有限元方法,并具体应用于某型导弹固体发动机药柱结构完整性分析。张为华[8]和蔡国飚[9]针对旋转载荷对固体火箭发动机药柱应力应变的影响开展了专门理论研究。D.Lancelle[10]介绍了德国宇航中心(DLR)为开展某火箭发动机在3 300g过载条件下的结构可靠性论证所进行

的数值模拟和飞行实验,最终实验结果与数值模拟较为吻合。郭振伏[11-12]和武智慧[13]分别对底排药柱在发射工况下的变形与强度开展研究,并就改善药柱结构完整性给出相应措施。

综上所述,采用线性粘弹性模型已得到较多有益结论,在此基础上,文中仍采用线粘弹性模型对某型高过载固体火箭发动机推进剂药柱进行数值模拟,分别对比研究轴向过载、旋转载荷和药柱-挡药板之间摩擦对药柱整体最大von Mises应力和最大应变的影响规律。

1 导弹在膛内运动阶段的运动规律

文中以某在研高膛压线膛炮炮射导弹为研究背景,发射过程中该导弹在承受极高轴向过载的同时弹体高速旋转。已知导弹在膛内运动期间,导弹整体所承受轴向过载随时间变化规律如图1所示,导弹转速随时间变化规律如图2所示。

2 物理模型与计算分析

2.1 固体推进剂的力学模型

固体推进剂是一种典型的含有固体填料的高分子聚合物,其力学性能呈明显的粘弹性特性。如果将其简化为各向同性线粘弹性材料,则其三维积分型线性粘弹性本构关系可表示为:

(1)

式中:σij为应力张量;εij为应变张量;K为体积模量;G为剪切模量;δij为狄拉克函数。当i=j时,δij=1,当i≠j时,δij=0。其中,G(t)和K(t)可分别表示为:

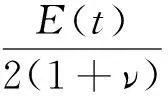
(2)

工程中通常采用松弛模量随松弛时间的衰减来表征固体推进剂的应力松弛过程。文中推进剂所采用的Prony级数松弛模量表达式为:

(3)

其中各参数详见表1。

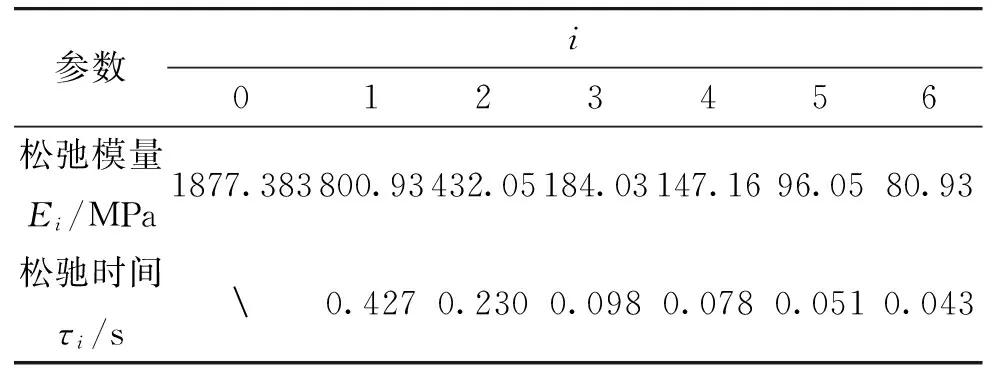
表1 固体推进剂松弛量Prony级数参数[14]

2.2 推进剂药柱的三维模型

该发动机采用管型自由装填推进剂药柱,其三维模型如图3所示。推进剂密度为1 650 kg/m3,泊松比为0.495。对推进剂药柱整体采用结构化网格划分方案,生成421 848个节点,399 900个三维实体8节点缩减积分单元。

2.3 边界条件与载荷

推进剂药柱自由装填于发动机燃烧室内,径向与发动机壳体之间的间隙为2 mm。由于发射时间极短,暂不考虑药柱温度变化,并将药柱与壳体温度均设定为20℃。为了分别揭示与对比旋转载荷和药柱-挡药板之间摩擦对于药柱整体应力应变变化趋势的影响规律,文中数值计算分别设计三组计算工况,依次为:工况A,药柱只承受如图1所示轴向过载,不考虑旋转和摩擦的影响;工况B,药柱承受如图1所示轴向过载,同时考虑药柱与发动机挡药板之间摩擦;工况C,药柱与发动机挡药板接触,摩擦系数为0.2,药柱同时承受如图1和图2所示轴向过载和旋转载荷。

2.4 计算结果与分析

对高过载条件下药柱结构进行完整性分析通常以强度作为判据,采用第四强度理论[5-6]。文中主要对比研究某型炮射导弹膛内运动过程中,在轴向载荷、旋转载荷和药柱挡药板之间摩擦力作用下,药柱应力应变变化规律,因而计算过程中始终监控最大等效von Mises应力与最大应变变化规律。

2.4.1 工况A

整个加载过程中最大等效von Mises应力与最大主应变均发生在推进剂药柱与挡药板相接触区域的内孔边缘处。在药柱与挡药板接触端面,应力和应变随着半径的增大而减小,在外边缘处达到最小。在轴向上,随着与受载端面之间距离增大,应力和应变逐渐递减。具体见图4和图5。

由图4和图5显见,A工况下,药柱与挡药板接触端存在较为明显的应力、应变集中。推进剂药柱与挡药板相接触区域的外边缘与内孔边缘处的最大von Mises应力和最大应变随时间变化规律对比具体如图6所示。

由图6显见,受载过程中,推进剂药柱与挡药板相接触区域的内孔边缘处的最大von Mises应力和最大应变均略高于相接触区域外边缘处。药柱与挡药板相接触区域的内孔边缘处的最大von Mises应力为49.051 MPa,最大应变为0.727%;药柱与挡药板相接触区域外边缘处最大von Mises应力为47.507 MPa,最大应变为0.688%。

2.4.2 工况B

受载过程中最大等效von Mises应力与最大主应变均发生在药柱与挡药板相接触区域的外边缘处。在药柱的受载端面,随着半径增大,应力和应变逐渐趋于增加,在外边缘处达到最大。药柱在轴向上,随着与受载端面距离的增加,应力和应变趋于逐渐减小。具体如图7和图8所示。

相对于A工况,药柱与挡药板接触端应力集中更为显著。推进剂药柱底部与挡药板相接触区域的外边缘与内孔边缘处的最大von Mises应力和最大应变随时间变化规律具体如图9所示。

由图9显见,考虑药柱与挡药板之间摩擦时,药柱与挡药板相接触区域的外边缘处最大von Mises应力和最大应变均显著高于内孔边缘处。药柱与挡药板相接触区域内孔边缘处的最大von Mises应力为27.778 MPa,最大应变为0.736%;药柱与挡药板相接触区域外边缘处最大von Mises应力为54.800 MPa,最大应变为1.075%。

2.4.3 工况C

整个受载过程中药柱与挡药板接触端外边缘最大等效von Mises应力和最大应变始终高于推进剂药柱内孔边缘处(应力、应变分布类似于工况B中图7和图8)。药柱与挡药板相接触区域的外边缘与内孔边缘处的最大等效von Mises应力和最大应变随时间变化规律具体如图10所示。

由图10显见,发射过程中,药柱与挡药板相接触区域外边缘处的最大等效von Mises应力和最大应变始终高于内孔边缘处。推进剂药柱与挡药板相接触区域的内孔边缘处的最大等效von Mises应力为29.000 MPa,最大主应变为0.843%;药柱与挡药板相接触区域外边缘处最大等效von Mises应力为56.300 MPa,最大应变为1.178%。

2.4.4 计算结果对比与分析

分别将上述3种计算工况下所得到的推进剂药柱内、外边缘处最大等效von Mises应力和最大应变进行对比,如图11所示。

结果表明,同时考虑旋转载荷和药柱底面-挡药板之间摩擦的情况下(工况C),相对于文献[2-6]中所采用的计算工况(工况A),药柱外边缘处最大等效von Mises应力和最大主应变均显著增加。由摩擦所引起的最大von Mises应力和最大应变的增加,相较于旋转载荷的影响更为强烈。

3 摩擦和转速对药柱最大von Mises应力和最大应变变化规律的影响

3.1 摩擦系数对药柱内部最大von Mises应力和最大应变变化规律的影响

在上述工况C基础上,依次调整药柱底面与挡药板之间摩擦系数为0、0.05、0.10、0.15、…、0.35分别统计药柱整体、药柱受载端内孔边缘和外边缘处最大von Mises应力和最大应变变化规律如图12所示。

由图12显见,当不考虑药柱底面与挡药板之间摩擦时,药柱内部最大等效von Mises应力和最大主应变分别等于药柱与挡药板接触端内孔边缘处的最大等效von Mises应力和最大应变。当摩擦系数从0、0.025、0.05依次增加至0.35时,药柱内部最大等效von Mises应力等于药柱与挡药板接触端外边缘处的最大等效von Mises应力,并且随着摩擦系数的增加而相应增加。药柱与挡药板接触端内孔边缘处的最大等效von Mises应力总体上趋于减小趋势。当摩擦系数从0.025、0.05、0.10依次增加至0.35时,药柱整体最大应变和药柱与挡药板接触端外边缘处的最大应变变化趋势趋于一致。

3.2 转速对药柱内部最大von Mises应力和最大主应变变化趋势的影响规律

在工况C基础上,依次调整导弹出炮口转速为2 500 r/min、3 000 r/min、3 500 r/min、…、5 500 r/min统计药柱最大von Mises应力和最大应变变化规律如图13所示。

由图13显见,导弹出炮口转速从2 500 r/min、3 000 r/min依次增加至5 500 r/min时,药柱内部最大von Mises应力和最大应变的增加相对于前述摩擦的影响而言极其微弱。

4 结论

文中分别对比研究了某型炮射导弹发射过程中轴向载荷、旋转载荷以及固体推进剂药柱-挡药板之间的摩擦对于药柱整体最大von Mises应力和最大应变的影响规律。具体结论如下:

1)考虑旋转载荷和药柱端面与挡药板之间摩擦的影响(C工况),相对于文献[2-12]中所采用的计算工况(A工况),药柱内部最大von Mises应力和最大应变都显著增加。

2)对于该管型药柱,不考虑推进剂药柱与挡药板之间摩擦的情况下(A工况),推进剂药柱最大von Mises应力和最大应变出现在药柱内孔边缘;考虑推进剂药柱与挡药板之间摩擦的情况下(B工况和C工况),推进剂药柱最大von Mises应力和最大应变出现在药柱底部与挡药板相接触区域外边缘处。

3)药柱内部最大von Mises应力和最大应变随导弹转速和药柱端面挡药板之间摩擦系数的增加而增加,摩擦的影响更为显著和强烈。

综上所述,在进行该类高过载固体推进剂药柱的数值计算时应该综合考虑轴向过载、旋转载荷和药柱挡药板之间摩擦对于药柱应力、应变的影响,从而更加接近炮射导弹在膛内运动过程中固体推进剂药柱的实际受载与应力应变状态。

[1] 苏维厚, 赵秀超, 张莉, 等. 抗高过载发动机装药技术 [C]∥中国宇航学会团体火箭推进专业委员会. 中国宇航学会2005年固体火箭推进第22届年会论文集：发动机分册. 成都：推进技术编辑部, 2005：102-104.

[2] 魏卫, 王宁飞. 高加速度冲击下固体推进剂药柱轴向形变的数值模拟 [J]. 固体火箭技术, 2003, 26(2): 42-45.

[3] 魏卫, 王宁飞. 轴向高过载下固体推进剂结构完整性数值模拟 [J]. 火炸药学报, 2004, 2(27): 53-55.

[4] 魏卫, 王宁飞. 固体推进剂在冲击载荷下力学行为的数值模拟 [C]∥中国宇航学会固体火箭推进专业委员会. 中国宇航学会2002年固体推进专业第19届年会论文集：发动机分册. 成都：推进技术编辑部, 2002：95-99.

[5] 隋欣, 魏志军, 王宁飞, 等. 炮射导弹发射过程发动机装药强度分析 [J]. 弹道学报, 2009, 21(2): 19-22.

[6] 隋欣, 魏志军, 王宁飞, 等. 炮射导弹发射过程中装药衬垫材料对抗过载能力的影响计算分析 [J]. 兵工学报, 2009, 30(6): 709-713.

[7] 唐国金, 周建平. 自由装填药柱的结构完整性分析 [J]. 固体火箭技术, 1994(2): 13-19.

[8] 张为华, 曹泰岳, 万章吉, 等. 旋转发动机研究中的几个重要技术问题 [J]. 推进技术, 1996, 17(3): 26-31.

[9] 蔡国飙, 田辉. 旋转对固体火箭发动机的影响 [J]. 推进技术, 1999, 20(1): 11-15.

[10] LANCELLE1 D, BOZIC O, KÖKE H. Flight test results of investigation of acceleration effects on a gun launched rocket engine [C]// EML. 2012 16th International Symposium on Electromagnetic Launch Technology. New York：IEEE, 2012.

[11] 郭振伏, 武晓松, 余陵, 等. 底排火箭复合增程弹助推火箭推进剂结构完整性分析 [J]. 弹道学报, 2003, 15(2): 34-38.

[12] 郭振伏. 复合增程弹助推火箭推进剂药柱结构完整性分析 [D]. 南京: 南京理工大学, 2002.

[13] 武智慧, 钱建平, 刘荣忠, 等. 实际发射工况下底排药柱结构完整性的模拟计算 [J]. 火炸药学报, 2014, 27(3): 60-65.

[14] 孟红磊. 改性双基推进剂药柱结构完整性数值仿真方法研究 [D]. 南京: 南京理工大学, 2011.

[15] 王宏丽, 鞠玉涛, 许进升, 等. 基于损伤型本构高过载下装药强度数值仿真方法研究 [J]. 推进技术, 2014, 35(5): 708-713.

[16] CHANG I-Shih. Adaptive, unstructured, solid propellant stress analysis [J]. Jounal of Spacecraft and Rockets, 1993,30(1):43-50.

[17] MORGAN J A. A brief history of cannon launch [C]//MORGAN J. 33rd AIAA Joint Propulsion Conference.[S.l.:s.n.], 1997.

[18] Solid propellant grain structural integrity analysis [S]. NASA space vehicle design criteria. New York:AIAA, 1973.

[19] SINGER Victor, SOIBERG Mark A. Design for a gun-launched rocket: US 6094906 [P]. 2000-08-01.

[20] BETTS Robert E, ZEMAN Samuel. Gun launch rocket propellant support filler: US 5708229 [P]. 1998-01-13.

[21] WALL Richard H. Rocket assisted projectile: US 3698321 [P]. 1972-10-17.

[22] BERT A R, LARS A, MALTE B S, et al. Rocket-assisted projectile or gun boosted rocket with supported propellant grain : US 3628457[P]. 1971-12-21.

StressandStrainAnalysisofaGun-launchedSolidRocketMotorPropellantGrainduringtheLaunchingProcess

WANG Haiqing1,2, SUI Xin1, DING Narenhua2, SONG Changjian2, LI Shipeng1, WANG Ningfei1

(1 School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China; 2 Aviation and Aerospace School, Tianjin Sino-German University of Applied Sciences, Tianjin 300350, China)

During the process of launching, the gun-launched rocket is always subjected to a very high overload, even more than 104g. Therefore, the stress and strain analysis of solid propellant grains is of great significance. In this paper, we used the finite element software to simulate the stress and strain of the grain structure during the launching process, conducting a comparative study on the effects of axial load, rotating load and grain-retaining plate friction on the maximum von Mises stress and maximum principal strain of the grain. The results showed that considering rotating load and the grain-retaining plate friction, the maximum von Mises stress and the maximum principal strain of whole grain will be significantly increased, and the grain-retaining plate friction will affect the distribution of maximum von Mises stress and the maximum principal strain.

gun-launched rocket; solid rocket motor; propellant grain; stress and strain analysis

V435

A

2016-05-15

王海清(1985-),男,内蒙古托克托人,硕士研究生,研究方向:固体火箭推进剂药柱结构完整性分析。