基于改进统计最优近场声全息的空间多种声源声场重建

2017-10-26赵报川杨涛张进

声学技术 2017年3期

赵报川，杨涛，张进

赵报川1,2，杨涛1,2，张进3

(1. 西南科技大学信息工程学院，四川绵阳 621010；2. 西南科技大学特殊环境机器人技术四川省重点实验室，四川绵阳 621010；3. 国网重庆市电力公司电力科学研究院，重庆 401123)

为获取空间多种声源声场信息，传统统计最优近场声全息需要较多高阶项数的波函数来重建声场，而随着波函数阶数的提高，该方法对误差的放大作用也越大；此外传统方法都采用与声源共形的全息测量面，限制了其应用范围。提出了一种基于平面测量的改进统计最优近场声全息方法，可在波函数阶数较低的情况下提高重建精度。首先通过分析空间多种声源的特点选取合适的波函数组合，然后用该组合求出声场传递矩阵，最后重建出目标声源声场。通过数值仿真验证了该方法的有效性和适用性。结果表明：该方法能够有效地降低重建所需波函数阶数，抑制高阶波数对误差的放大作用从而提高重建精度，即使全息面与声源不共形，也能准确地重建出目标声源声场。

统计最优；近场声全息；波函数

0 引言

噪声源的准确识别是进行噪声控制的首要条件，而近场声全息技术(Near-field Acoustical Holography，NAH)是声源识别的重要技术之一。通过在近场测量复声压数据，不仅可以重建出声源表面的声压、振速、声强等声学量，也可以对空间声场中任意点处的声学量进行重建与预测。由于是在近场测量，获取了随传播距离呈指数规律衰减的倏逝波成分，因而重建和预测的分辨率很高。经过30多年的发展，已经由最初的基于空间傅里叶变换的NAH技术[1]，发展到边界元法[2]、等效源法[3]和统计最优NAH[4]等多种算法，且在实际应用中的范围也越来越广。

统计最优近场声全息(Statistically Optimized Near-Field Acoustical Holography，SONAH)作为一种典型的局部近场声全息算法，直接通过空间域中全息面上测量声压的线性叠加来计算重建面上的声学量。其叠加系数矩阵可由单元波函数在全息面与重建面之间的映射关系得到，常用的单元波函数主要有平面波函数、柱面波函数和球面波函数等，相应地发展出统计最优平面、柱面和球面近场声全息等技术[4-6]。在此基础上，经过国内外学者的研究，该方法也已从单一的利用声压信息扩展到利用振速信息进行声场重建[5,7]，由自由空间声场重建拓展到非自由空间声场的重建等[8-9]，这些新进展都大大拓展了该算法的应用范围。此外，由于在重建过程中不存在卷积运算，因而从根本上消除了基于空间傅里叶变换SONAH中所固有的窗效应和卷绕误差等问题[10-11]。

虽然该方法受到众多学者的关注，但无论在算法理论上还是实际应用中，都还局限于利用单一类型的单元波函数来研究重建空间声场。如Yong Thung Cho[12]等人将平面SONAH扩展到柱面SONAH，用比平面SONAH更少的测量点数重建出制冷压缩机这种柱形声源的辐射声场；张永斌[13]等人提出了一种单元平面波优化选择方法，提高了SONAH的计算速度和重建精度；杨洋[14]等人详细分析了阵列形式及阵元失效对统计最优近场声全息重建结果的影响。但如果空间中存在多个不同类型的声源，如多个声源同时产生了平面波和柱面波，这时若只采用单元平面波来重建空间声场，则需要更高阶数的单元平面波才能得到理想的重建精度。但随着阶数的提高，测量点数增多，计算量也随之增大。另外，由于高阶波数矢量对误差的放大作用，过高的阶数甚至会使重建失效，因此如何有效降阶是SONAH中的一大难点。此外，全息测量面大都选择与声源共形，即若采用统计最优柱面近场声全息，则全息面也设计为柱面，若为球面，则全息面也为球面。上述局限性限制了SONAH的应用范围。

针对以上情况，本文提出了一种基于平面测量的适用于多声源统计的改进SONAH算法，其基本思想为：首先，根据声源类型来选择波函数组合，然后以这些波函数组合在全息面与重建面之间的映射关系计算出SONAH中的传递矩阵，最后再利用全息平面上测量的复声压来重建或预测空间声场中的声压、振速等声学量。数值仿真结果表明该方法可有效降低所需波函数的阶数，且具有重建精度高、计算量小等优点。

1 SONAH基本原理

根据波场叠加原理可知：重建面上任意点处波数矢量为的单元波函数，可由在全息面上所有点处波数矢量同为的单元波函数叠加得到[10]，即：

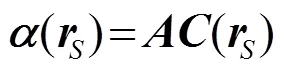
式中，

式(4)的标准Tikhonov正则化解为[10]

2 改进SONAH原理

理论上讲，对于一组满足声波场Helmholtz方程且具有完备性的波函数集合来说，可以用这一组波函数的线性组合来逼近任意声场。例如，只要选取的波函数项数足够多，就可利用单元平面波的线性叠加来逼近一脉动球源产生的声场。但在实际实现中，由于受全息面上测量点数和数值计算等方面的限制，只能从这一完备的波函数集合中选取项数有限的子集来逼近实际声场。通常情况下，若选取的波函数集与声源共形，则可用更少的波函数项数来精确逼近声场，同时降低了计算量，提高了计算效率。这也是采用单元平面波来计算平面声源，采用单元球面波来计算紧致声源产生声场的原因。基于以上思想，提出了一种改进SONAH重建空间中存在多种不同类型声源时声场的重建方法。

设共有个波函数集，全息面和重建面处有个单元波函数数目，此时，波函数类型及单元波函数数目可以不相同，则在全息面上个测量点处的每个单元波函数为

同理，重建面上的单元波函数为

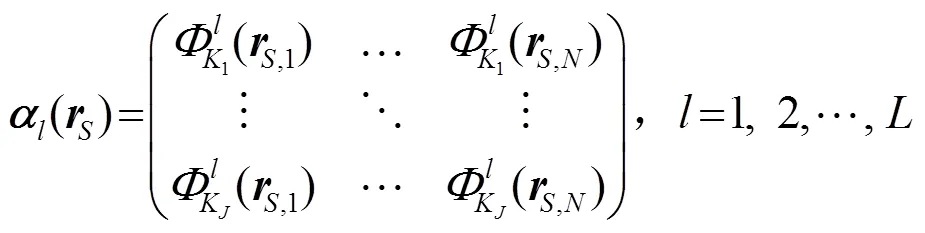
将这个单元波函数矢量矩阵垂直串接，可得到这组波函数集的矩阵，分别简写为以下形式:

改进算法的重建公式虽然与常规算法的重建公式形式一样，但存在着本质的不同。主要为改进算法中的声场传递矩阵是由不同的单元波函数组合来进行求解，而常规算法仅由单一的单元波函数进行求解。

常见的波函数主要有平面、柱面、球面以及椭球面波函数等。不失一般性，本文选用前三种波函数作为研究对象。通过根据声源的形状与个数来选取所需要的波函数组合，然后使用这些波函数组合可用较低的阶数计算出SONAH的传递矩阵，进而重建出声场。本文所涉及的三种单元波函数定义如下。

在笛卡尔坐标系下，单元平面波定义为

其中，

在柱坐标系下单元柱面波定义为

在球坐标系下单元球面波定义为

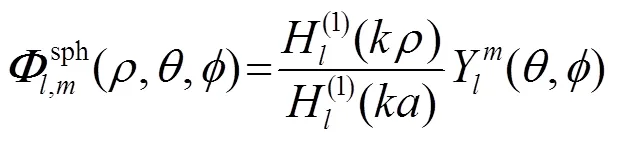
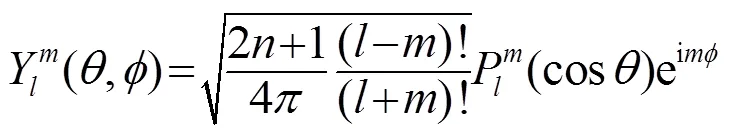
3 仿真验证

下面将通过两组数值仿真实验来验证该方法的有效性。其中，全息面位于=0.25 m处，测量间距为0.05 m，测量点数为21´21。重建面位于=0.15 m，大小及测量点数与全息面相同。

以下列出的是要用到的波函数集以及笛卡尔坐标系与各坐标系之间的转换关系。

平面波函数：

柱面波函数1：

柱面波函数2：

球面波函数：

3.1 仿真1

如图1所示，目标声源为两列线阵声源，线阵声源1的坐标为(,)=(0, 0.25)，线阵声源2的坐标为(,)=(0,-0.25)，这两个线阵声源分别由51个点源构成，且在=-0.25 m至0.25 m之间等间距分布。

为了更好地模拟柱状声源的实际声场，对两线阵声源产生的声场加一权重系数，定义为

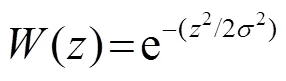
其中，=0.5。两线阵声源产生的声场为各点源产生的声场的叠加，每个点源的振动频率=1 000 Hz，振动速度为1 m/s，声速为343 m/s，空气密度=1.21 kg/m3。在仿真过程中加入了45 dB的随机噪声。

图1 仿真1中的声源配置

Fig.1 Sound source configurations in the first simulation

分别使用统计最优平面近场声全息(Statistically Optimized Planar Nearfield Acoustical Holography，SOPNAH)和统计最优柱面近场声全息(Statistically Optimized Cylindrical Nearfield Acoustical Holography，SOCNAH)以及本文所述的改进SONAH进行重建。

其中，SOPNAH使用上文中的平面波函数进行声场重建，即：

SOCNAH使用前述中的柱面波函数1进行声场重建，即：

而改进SONAH使用前述的柱面波函数1 和柱面波函数2组合进行声场重建，即：

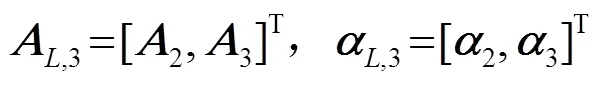
将式(15)、(16)、(17)分别代入式(11)即可求出声压的传递系数矩阵，进而利用式(12)即可求得重建面上的声压。图2给出了采用不同方法时的重建结果。

图2(a)是重建面上的理论值，图2(b)是采用传统的SOPNAH的重建结果，图2(c)是SOCNAH的重建结果，图2(d)是使用本文所述改进SONAH的重建结果。

由图2(c)可看出，只使用柱面波函数1的SOCNAH方法的重建结果远远大于理论值，重建面的声压分布完全淹没在了重建误差之中，这是因为所选的波函数集有限以及重建误差的影响使之无法有效地重建出目标声源声场。而采用SOPNAH和改进SONAH都能较为准确地重建出目标声源的声场，但改进的SONAH对理论值跟随性更好，重建精度也要优于SOPNAH。其中，SOPNAH的总体重建误差为15.27%，而改进SONAH法的总体重建误差只有3.45%。为了能更清楚地显示重建结果与理论值的偏差，图3仅显示出了沿=0处重建面上的理论声压幅值、SOPNAH以及使用本文所述的改进SONAH重建声压幅值。由图3可以看出，在三个声压峰值处，基于SOPNAH的重建结果要小于理论值和改进SONAH的重建值。

(a) 重建面理论值

(b) SOPNAH重建值

(d) 改进SONAH重建值

图2 重建面理论值及不同方法的重建值(仿真1)

Fig.2 Theoretical values and reconstructed results of SOPNAH, SOCNAH and improved SONAH for Simulation 1

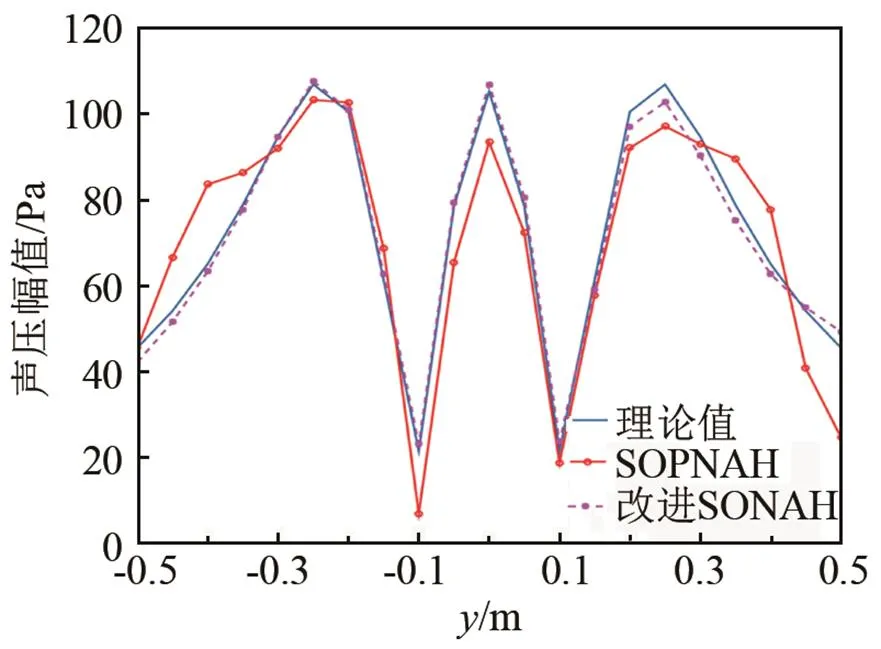
图3 SOPNAH和改进SONAH重建结果与理论值的比较(仿真1)

由SONAH的基本理论可知[10]，重建误差随着波数的增大而增大，因而在重建过程中需使用正则化来抑制高波数成分带来的重建误差，这就导致了部分高波数成分信息的丢失，从而使重建结果比实际值偏小。而改进SONAH较为有效地避免了该问题，这是因为改进SONAH选取的波函数与声源共形，用较低阶数的波函数就能精确地反映出目标声源产生的声场，这也是改进SONAH的一大优势。

3.2 仿真2

为验证本方法的适用性，在仿真1所述目标声源基础上再添加一脉动球声源，声源配置如图4所示。其中，脉动球源的半径为0.08 m，球心位于(,,)=(0, 0,-0.3)处，振动频率为1 000 Hz，全息面与重建面同仿真1。分别使用SOPNAH和两种改进SONAH重建目标声源的声场，重建过程中同样加入了45 dB的随机噪声。

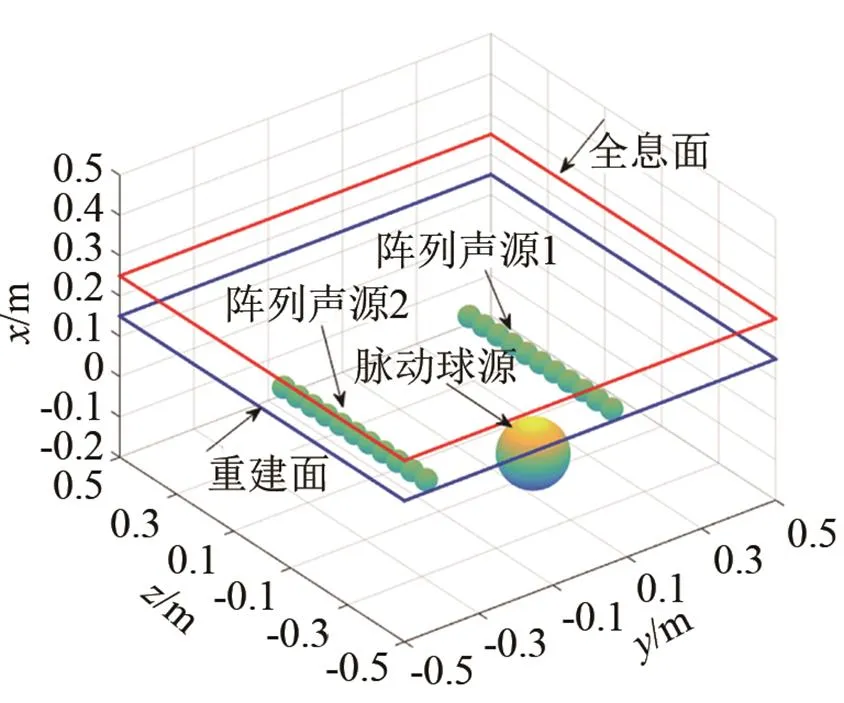
图4 仿真2中的声源配置

第一种改进SONAH选用的波函数与仿真1中式(20)的相同，即只使用单元柱面波函数组合的改进SONAH (组合1 SONAH)；而第二种组合使用单元柱面波函数1、2和单元球面波函数进行重建(组合2 SONAH)。可得

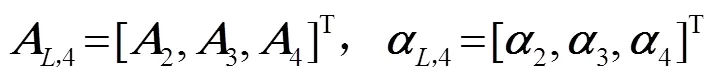
进而求出重建面上的声压，重建结果如图5所示。

(a) 重建面理论值

(b) SOPNAH重建值

(d) 组合2改进SONAH重建值

图5中，SOPNAH的总体重建误差为19.22%，组合1 SONAH的总体重建误差为14.62%，而使用柱面波函数与球面波函数组合的组合2 SONAH的总体重建误差为11.81%。不难看出，采用传统SOPNAH的重建效果比两种改进SONAH的重建结果都要差。图6则更为清晰地显示出各重建值与理论值之间沿=0时的声压幅值。由以上分析可知，根据目标声源的特点，合理选择波函数组合能更为有效且更为准确地重建出目标声场。

图6 SOPNAH和改进SONAH重建结果与理论值的比较(仿真2)

4 结论

为了能够有效地重建出空间中含有多种声源的声场，在传统的SONAH方法的基础上，提出了一种改进SONAH方法。首先，根据声源的特点，选取能够匹配声源形状和数量的波函数。之后，同传统的SONAH计算方法和步骤一样，利用选取的波函数组合计算声场传递矩阵，最终重建出目标声源的声场。该方法能够有效地降低重建过程中所需的波函数阶数，从而减少了计算量，且重建精度高。数值仿真结果证明了该方法的有效性和适用性。此外，由于传统的SONAH方法只使用一种波函数，全息面测量面也都选择与声源共形，而本文所提方法中选取的波函数可能既有柱面波函数也有球面波等多种不同类型，全息面要做到与声源共形难度很大，因而本文所用全息面均设为平面，仿真结果也证明了即使全息面与声源不共形，该方法也能准确地重建出目标声源的声场。本文所提方法需要具有目标声源特点的先验知识，以此来指导波函数的选取，但对于未知的目标声源，则可结合波束形成法等其它声源识别方法来指导配置。

[1] Maynard J D, Williams E G, Lee Y. Near field acoustic holography: I. theory of generalized holography and the development of NAH[J]. J. Acoust. Soc. Am., 1985, 78(4): 1395-1413.

[2] Veronesi W A, Maynard J D. Digital holographic reconstruction of sources with arbitrarily shaped surfaces[J]. J. Acoust. Soc. Am., 1989, 85(2): 588-598.

[3] BI C X, Stuart Bolton J. An equivalent source technique for recovering the free sound field in a noisy environment[J]. J. Acoust. Soc. Am., 2012, 131(2): 1260-1270.

[4] Steiner R, Hald, J. Near-field acoustical holography without the errors and limitations caused by the use of spatial DFT[J]. International Journal of Acoustics and Vibration, 2001, 6(2): 83-89.

[5] Cho Y T, Bolton J, Hald J. Source visualization by using statistically optimized near-field acoustical holography in cylindrical coordinates[J]. J. Acoust. Soc. Am., 2005, 118(4): 2355-2364.

[6] 李卫兵, 陈剑, 毕传兴, 等. 统计最优球面近场声全息在噪声源识别中的应用[J]. 振动工程学报, 2004, 17(S): 959-961. LI Weibing, CHEN Jian, BI Chuanxing, et al. Statistically optimal spherical near-field acoustical holography for noise source identification[J]. Journal of Vibration Engineering, 2004, 17(S): 959-961.

[7] 胡博，杨德森. 基于矢量阵测量的局部近场声全息技术研究[J]. 振动与冲击, 2011, 30(8) : 225-229. HU Bo, YANG Desen. Patch near-field holography study based on measurement of vector hydrophone array[J]. Journal of Vibration and Shock, 2011, 30(8): 225-220.

[8] Jacobsen F, Jaud V. Statistically optimized near field acoustic holography using an array of pressure-velocity probes[J]. J. Acoust. Soc. Am., 2007, 121(3): 1550-1558.

[9] 毛锦, 徐中明, 贺岩松, 等. 统计最优双面声场分离的改进算法[J]. 机械工程学报, 2015, 51(15): 129-134. MAO Jin, XU Zhongming, HE Yansong, et al. The modified algorithm of sound field separation with double planes based on statistically optimal method[J]. Journal of Mechanical Engineering, 2015, 51(15): 129-134.

[10] Hald J. Basic theory and properties of statistically optimized near-field acoustical holography[J]. J. Acoust. Soc. Am., 2009, 125(4): 2105-2120.

[11] Hald J. Scaling of plane-wave functions in statistically optimized near-field acoustic holography[J]. J. Acoust. Soc. Am., 2014, 136 (5): 2687-2696.

[12] Cho Y, Bolton J S. Source visualization by using statistically optimized near-field acoustical holography in cylindrical coordinates[J]. J. Acoust. Soc. Am., 2005, 118(4): 2355-2364.

[13] 张永斌，毕传兴，张小正. 统计最优近场声全息重建精度和计算速度优化方法[J]. 声学学报, 2014, 39(2): 192-198. ZHANG Yongbin, BI Chuanxing, ZHANG Xiaozheng. The mothod for improving the reconstruction accuracy and computational speed of the statistically optimized nearfield acoustic holography[J]. Acta Acustica, 2014, 39(2):192-198.

[14] 杨洋, 蔡鹏飞, 褚志刚. 阵列形式及阵元失效对统计最优近场声全息重建结果的影响分析[J]. 声学技术, 2014, 33(4): 352-358. YANG Yang, CAI Pengfei, CHU Zhigang. The influence of array geometry and element failure on SONAH reconstruction results [J]. Technical Acoustics, 2014, 33(4): 352-358.

[15] Hald J. Patch near-field acoustical holography using a new statistically optimal method[C]//Proceedings of Inter-Noise 2003, 2003: 2203- 2210.

Sound field reconstruction of multi-types of spatially sources by improved statistically optimized near-field acoustical holography

ZHAO Bao-chuan1,2, YANG Tao1,2, ZHANG Jin3

(1. Southwest University of Science and Technology, Mianyang 621010, Sichuan, China; 2. Southwest University of Science and Technology, Robot Technology Used for Special Environment Key Laboratory of Sichuan Province, Mianyang 621010, Sichuan, China;3. State Grid Chongqing Electric Power Research Institute, Chongqing 401123, China)

To reconstruct the sound field generated by multi-types spatially sound sources, the conventional statistically optimized near-field acoustical holography (SONAH) needs high-order terms to represent the sound field, and the high-order terms are more susceptible to noise contamination. Furthermore, the conventional SONAH is usually required to be conformal with the shape of sound source, and the hologram measurement surface of this technique is usually planar. This paper presents an improved SONAH which can reconstruct the sound field accurately in low-order terms. Firstly, a set of wave functions are selected depending on the features of spatial sound sources. Then, the transfer function matrix is calculated by using the wave function set to reconstruct the sound field. Numerical simulations are used to demonstrate the validity and applicability of this approach. The results show that the number of wave function orders can be reduced and thus the errors caused by high-order terms can be restrained to obtain more accurate results than that by using the conventional SONAH method. The proposed technique can be used to reconstruct the sound field accurately even when the hologram measurement surface is not conformal with the sound source.

statistical optimization; near-field acoustical holography; wave function

TB535

1000-3630(2017)-03-0203-07

10.16300/j.cnki.1000-3630.2017.03.002

2016-06-15;

2016-10-14

国家自然科学基金资助项目(F011102)、特殊环境机器人技术四川省重点实验室开放基金(13zxtk06)

赵报川(1989－), 男, 河北邯郸人, 硕士研究生, 研究方向为声学信号处理。

杨涛, E-mail: yangtao@swust.edu.cn