基于改进遗传算法的海底地层参数反演计算
2017-10-26刘波王晓峰张春雷
刘波,王晓峰,张春雷
基于改进遗传算法的海底地层参数反演计算
刘波,王晓峰,张春雷
(大连测控技术研究所,辽宁大连116013)
为了提高对海底地层参数变量的反演计算能力,设计了一种基于双种群协同进化策略的改进遗传算法。针对标准遗传算法局部搜索能力差且易于出现早熟现象的缺点,在标准遗传算法基础上引入双种群同时进行优化搜索,两个种群分别给予不同的控制参数,实现协同进化,最终给出一个综合的最优解。通过两个算例对遗传算法的寻优能力进行测试,实验结果表明,提出的改进算法不仅提高了搜索性能,并且对遗传控制参数的依靠度大大降低,特别是对大型复合参数反演问题的求解计算更为有效。
海底地层参数;水声反演;改进遗传算法;协同进化;搜索能力
0 引言
目前,声波是海洋中进行远距离信息传输最有效的传播形式。因此,利用海洋声学来研究海洋特性具有十分重要的意义。在海洋中影响声波传播规律的因素有很多,如海水的温度、盐度、海面的波动、海底厚度、海底地层质地结构等。其中,由于海底底质的声学特性参数很难直接测量,严重影响了海洋声场的准确预报、声呐作用距离的估算和水下声源空间位置的精确定位。如何快速、准确地得到海底的声学特征参数已成为人们关注的热点,国内外学者对此提出了许多行之有效的测量技术和方法。近年来,水声反演技术得到了广泛的研究应用[1]。水声反演是指在海洋物理特性的直接测量中获得信息,并结合水声学的理论模型,从稀疏的物理测量中估计水声场的特征参数的一种测量方法。水声反演的数学模型是求解一个非线性最小二乘问题,解算该类问题的最有效方法是采用优化算法。传统的优化方法在反演技术中存在许多缺点,很难在实际工程中得到应用[1]。随着计算机技术的发展,基于智能计算的参数反演方法得到了快速的发展,寻找反演技术中非凸问题的全局最优解得到了较好的解决[2]。以仿生学为基础的智能进化算法如遗传算法[3-4]、蚁群算法[5]、粒子群算法[6]等在反演技术中得到了广泛的应用。与传统的数学求解优化问题相比较,智能算法具有使用简便、不依赖于求解问题的数学特征,以及全局寻优能力强等优点。但是,当面对规模较大的复杂系统优化设计问题时,标准遗传算法往往会出现早熟现象,因而很难搜索到全局最优解,甚至得不到工程应用中的可靠解。为了解决这一困难,在采用标准遗传算法进行参数反演计算时大都需要改进。本文针对标准遗传算法在求解反问题过程中出现的迭代时间长、收敛速度慢和易于陷入局部极值等现象,对其进行了局部的改进以提高算法的稳定性。
1 设计海底地层参数反演的计算模型
对于海底的反演模型,为了简化起见,假设海底分为三层,有限层为两界面,即沉积一层和沉积二层,第三层为半无限的基底层。实验时,声源布设在水下5 m处,水听器水平直线阵位于水下5 m处,阵元间距为20 m,声源与海底距离为35 m,声源与第一个水听器的水平距离为368 m,具体结构及参数如图1所示。图1给出了本实验的布置情况和海底底质的分层结构。海底的沉积一层多是由淤泥、细沙和火山灰等物质组成,声波传播速度比海水层中的声速稍大;沉积二层一般由粗砂、砾石和泥土等构成,声速传播较大;基底层为岩石层,声速比沉积二层中的更大。
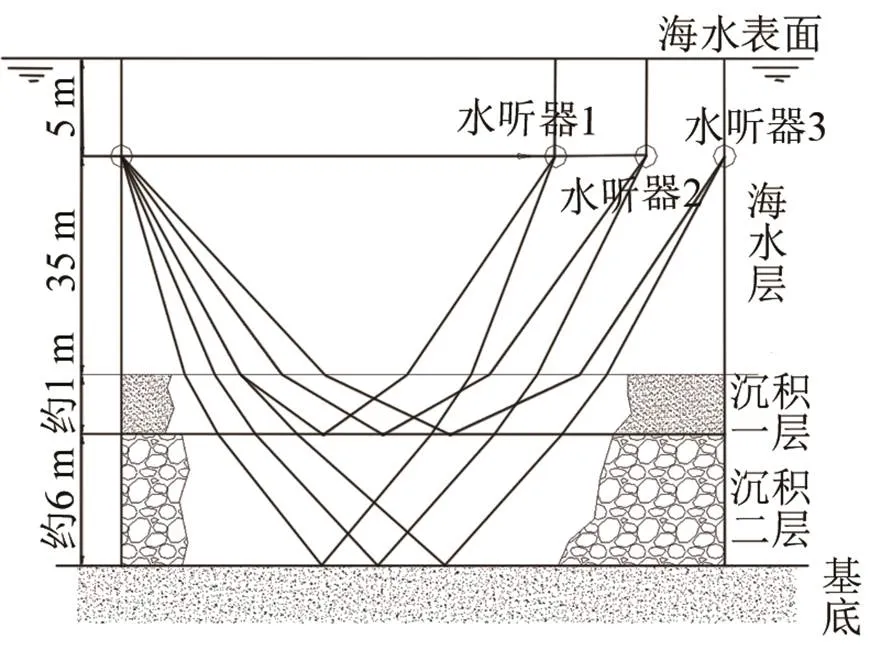
图1 海底地层参数反演模型示意图
依据图1,给合参考文献[7],设计本文算法的反演计算模型。声波自声源至接收点传播过程中所经路径,及其在各个界面处的投射角如图2所示,图2是仿真中经搜索本征声线后所绘制的声线图。该图是利用程序来实现的,是图1的简化,但给出了声线在各个界面的传播形式。
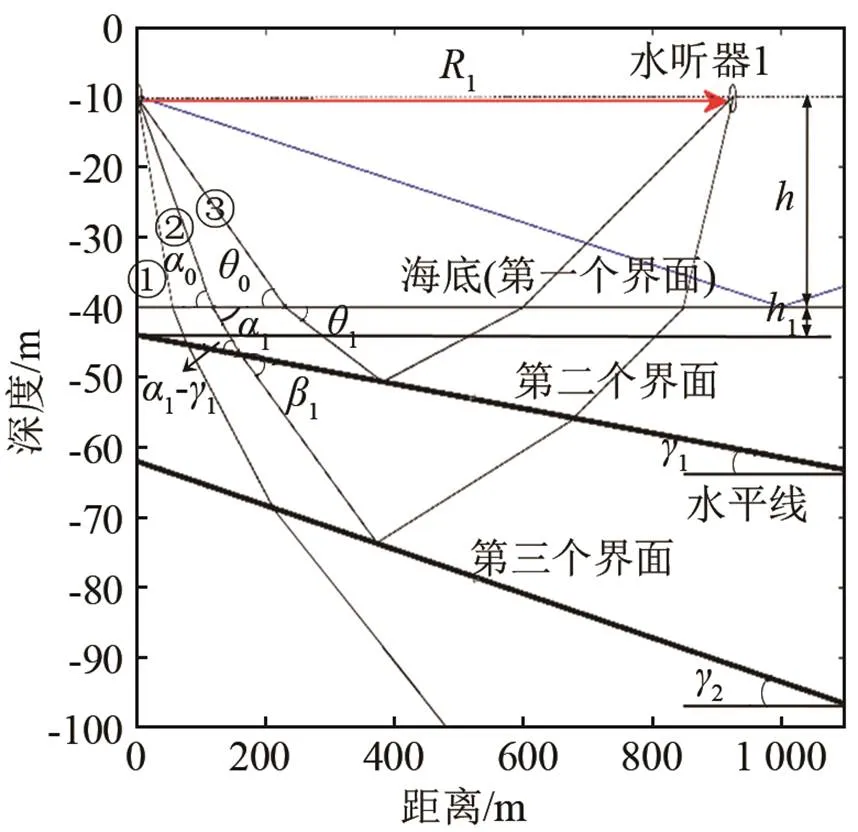
①为第一根声线;②为第二根声线;③为第三根声线。
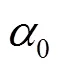
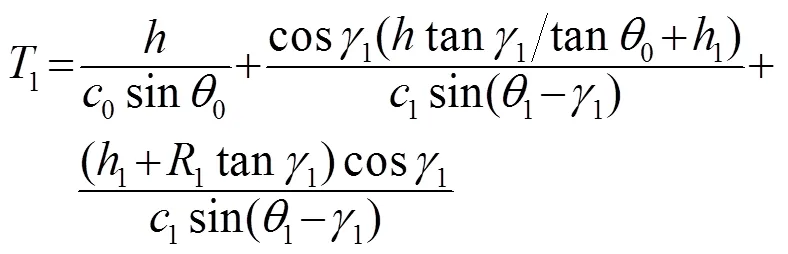
第一个水听器接收点距声源水平距离为

根据Snell定律

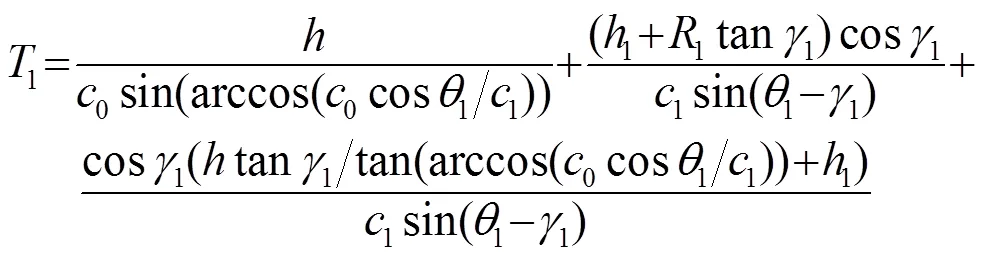

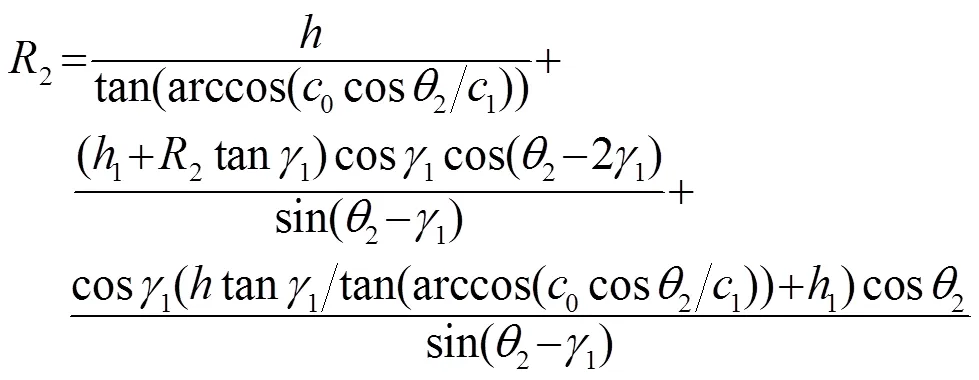


这样将有六个方程式和五个未知数,在具体联立方程式时声线传播时间选用时延形式,即


2 改进遗传算法求解反问题
针对标准遗传算法存在早熟收敛问题,本文提出一种改进的遗传算法替代标准遗传算法来解决参数反演中反问题的求解方法。由于单个种群在进行进化时,群体变化单一,交叉操作所产生的新个体存活时间较短,群体的更新只能依靠变异算子来保证。因此,本文引用双种群的策略解决上述问题。
首先,初始化产生两个子种群,两个子种群采用同样的轮盘赌选择策略、单点交叉算子和点位变异算子,但是各个种群中的交叉概率和变异概率可以选择不同的控制参数。其次,当两个子种群进化到一定代数以后,各个子种群中的最优个体将会显现,应把这些最优个体进行融合保留,并分享到每一个群体中,这一操作可以由协同进化算子来完成,协同进化算子的功能,在编程时是由目标种群中的最差个体用原种群中的最优个体代替。最后,将两个子种群的最优个体进行保存,这些新的最优个体是算法终止的判据。通过这种操作,可以使改进后的算法更有效地向最优解收敛。
标准遗传算法的实现思想可参考文献[8],下面仅给出标准遗传算法的算法流程和改进后的遗传算法的计算流程图,如图3和4所示。

图3 标准遗传算法流程

图4 改进遗传算法流程

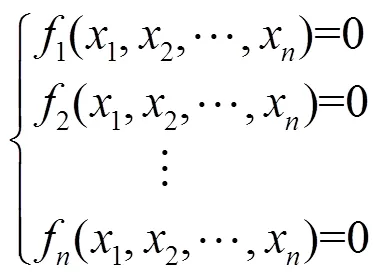

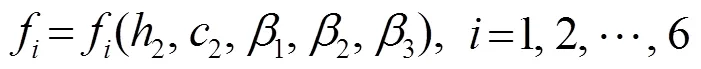
求解此方程组等价于求解下面的数值极值优化问题
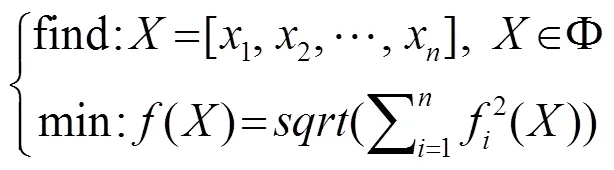
3 实验算例及结果分析
为了说明采用标准遗传算法解决海底地层参数反演计算问题的有效性与可行性,本文以一个带约束条件的数值优化模型为例进行说明。
3.1 带约束条件的数值优化模型
求解如下约束优化问题[9]:


图5 目标函数曲面与约束函数曲面
Fig.5 The surfaces of objective function and constraint function
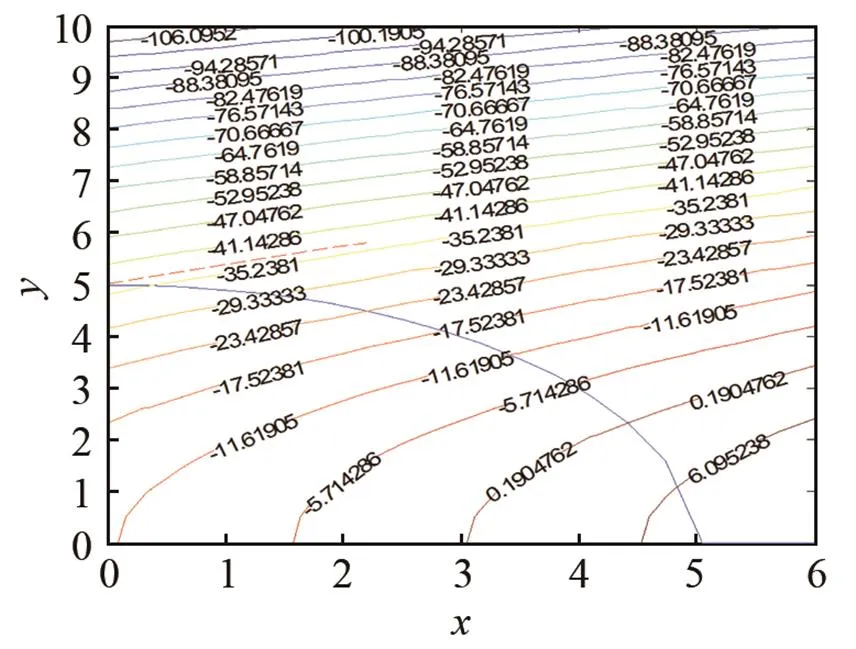
图6 函数优化结果
针对本算例,应用惩罚函数方法构造的适度值函数为


表1 数值优化结果
3.2 海底地层参数反演计算的遗传算法求解问题

表2 五个变量搜索空间范围

沉积二层h2/mc2/(m/s)β1/radβ2/radβ3/rad 上限72 1000.150.150.15 下限11 750000
下面给出了沉积一层和二层的初始解空间(种群)的分布图,如图7和图9所示;最终运行的解空间的分布变化如图8和图10所示。

(a) 深度空间解分布
(b) 声速空间解分布
图7 沉积一层初始解空间分布
Fig.7 The spatial distribution of initial solution in the first sedimentary layer
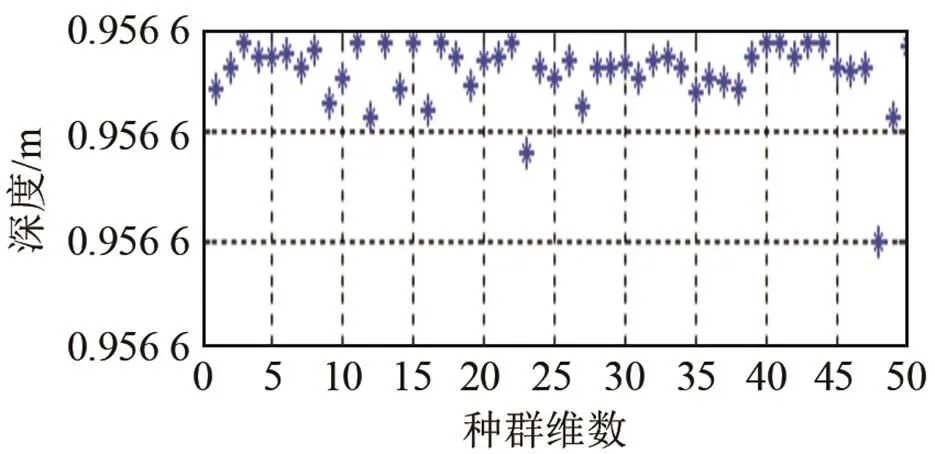
(a) 深度空间解分布
(b) 声速空间解分布

(c) 目标函数值空间解分布

(a) 深度空间解分布
(b) 声速空间解分布
图9 沉积二层初始解空间分布
Fig.9 The spatial distribution of initial solution in the second sedimentary layer

(a) 深度空间解分布
(b) 声速空间解分布

(c) 目标函数值空间解分布
图11和图12分别给出了计算沉积一层和沉积二层时的进化过程及运行收敛结果,图11、12中的终止代数均为500。

图11 沉积一层迭代收敛曲线

图12 沉积二层迭代收敛曲线
采用改进遗传算法对上述反问题进行求解时,其迭代过程收敛曲线如图13和图14所示,图中最优解的变化应从接近于0的某一值开始逐步向0靠近,终止代数均为52。通过与标准遗传算法的对比,可以看到改进算法对克服早熟收敛具有显著的效果。

图13 沉积一层迭代收敛曲线(改进算法)

图14 沉积二层迭代收敛曲线(改进算法)
反演计算模型利用遗传算法及其改进算法进行50次蒙特卡洛计算后,目标函数值和五个变量的平均值如表3和表4所示。
从图11和图12可以看出,标准遗传算法进行接近500次迭代后,优化解果才能稳定下来。而从图13和图14可知,改进遗传算法的优化进程短,收敛速度快,解的稳定性好,所用的遗传代数小,最大的也不超过60代。由表3和表4中目标值可以看出,改进遗传算法的求解结果更加准确,因而更适合复杂问题的优化。

表3 沉积一层遗传算法反演结果
注:GA-标准遗传算法;MGA-改进遗传算法

表4 沉积二层遗传算法反演结果
注:GA-标准遗传算法,MGA-改进遗传算法
4 结论
通过本文实验算例的验证,可见采用改进遗传算法对海底地层参数进行反演计算是可行的,且计算速度较快。本文提出的改进算法基于标准遗传算法框架,采用双种群同时对解空间进行协同搜索,提高了遗传算法的搜索性能,也使得计算结果对遗传控制参数的依靠度大大降低。本文算法对于大型复杂的参数反演问题求解计算,其效果尤为明显,从本文实例也可看出,在收敛速度和求解结果上,改进算法优于标准遗传算法。
此外,反演计算模型是本文遗传算法顺利进行的基础。在反问题求解实例中,时延值是通过实验得到的,而且时延值由公式(9)代入矛盾方程后,可求得优化目标的适应度函数。因此,时延数据值的准确选取比较关键,其对算法求解结果的影响较大。
[1] LI Jingsheng, Derek Elsworth. A modified Gauss Newton method for aquifer parameter identification[J]. Ground Water, 1995, 33(4): 662-668.
[2] 朱稣骥, 顾学康, 胡嘉骏. 遗传算法的改进及其在超大型油船结构优化中的应用[J]. 船舶力学, 2007, 11(2): 237-249. ZHU Suji, GU Xuekang, HU Jiajun. Modification of genetic algorithm and its application in ship structural optimal design of a VLCC[J]. Journal of Ship Mechanics, 2007, 11(2): 237-249.
[3] HUANG Chenfen, Peter Gerstoft, William S Hodgkiss. Effect of ocean sound speed uncertainty on matched-field geo-acoustic inversion[J]. J. Acoust. Soc. Am., 2008, 123(6): 162-168.
[4] Siderius, Nielsen, Sellschopp, Snellen, et al. Experimental study of geo-acoustic inversion uncertainty due to ocean sound-speed fluctuations[J]. J. Acoust. Soc. Am., 2001, 110(110): 769-781.
[5] 李守巨, 刘迎曦, 孙慧玲. 基于蚁群算法的含水层参数识别方法[J]. 岩土力学, 2005, 26(7): 1049-1053. LI Shouju, LIU Yingxi, SUN Huiling. Estimation of aquifter parameters using ant colony optimization[J]. Rock and Soil Mechanics, 2005, 26(7): 1049-1053.
[6] 朱童, 李小凡, 李一琼, 等. 基于改进粒子群算法的地震标量波方程反演[J]. 地球物理学报, 2011, 54(11): 2951-2959. ZHU Tong, LI Xiaofan, LI Yiqiong, et al. Seismic scalar wave equation inversion based on an improved particle swarm optimization algorithm[J]. Chinese Journal of Geophysics, 2011, 54(11): 2951-2959.
[7] 陈托. 水平阵海底地层参数反演研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. CHEN Tuo. Research on inversion of sea bottom parameters using a horizontal line array[D]. Harbin: Harbin Engineering University, 2008.
[8] 玄光男, 程润伟. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2003. XUAN Guangnan, CHENG Runwei. Genetic algorithms and engineering optimization[M]. Beijing: Tsinghua University Press, 2003.
[9] 雷英杰, 张善文. MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2006. LEI Yingjie, ZHANG Shanwen. MATLAB genetic algorithm toolbox and its application[M]. Xi’an: XiDian University Press, 2006.
Inversion calculation of sea bottom parameters based on improved genetic algorithm
LIU Bo, WANG Xiao-feng, ZHANG Chun-lei
(Dalian Scientific Test and Control Technology Institute, Dalian 116013, Liaoning, China)
In order to improve the inversion calculation of the sea bottom parameters variables, an improved genetic algorithm used for double populations’ co-evolutionary strategy is presented in this paper. In view of standard genetic algorithm has low efficiency in local extreme searching and might be easily premature phenomenon, the two populations are introduced to optimization based on the standard genetic algorithm, two populations are given with different control parameters to achieve co-evolution, and finally a comprehensive optimal solution is given in the text. By two examples to test the efficiency and practicability of the algorithm, the experimental results show that the proposed algorithm not only improves the search performance, but also greatly reduces the dependence on genetic control parameter, especially it is more effective to solve the large complex parameter inversion calculation problem.
sea bottom parameters; underwater acoustic inversion; improved genetic algorithm; co-evolutionary strategy; searching ability
TB556
A
1000-3630(2017)-03-0210-07
10.16300/j.cnki.1000-3630.2017.03.003
2016-08-16;
2016-12-08
国防基础科研基金项目(51310040203)
刘波(1977-), 男, 吉林通化人, 博士, 工程师, 研究方向为舰船振动噪声检测。
刘波, E-mail: liubo_1977@126.com
