简单均匀分布参数同等最短置信区间的求法
2017-10-19马艺光赵志文孙耀东
徐 宝,马艺光,赵志文,孙耀东
(吉林师范大学 数学学院,吉林 四平 136000)
简单均匀分布参数同等最短置信区间的求法
徐 宝,马艺光,赵志文,孙耀东
(吉林师范大学 数学学院,吉林 四平 136000)
对形如U(0,θ)的均匀分布,文章在给定置信水平1-a下,用计算函数极值的方法得到了参数q的平均长度最短的同等置信区间,然后通过最大密度区间法得到了该参数的相同的最短置信区间,后者的求解过程也充分印证了该方法也是确定参数最短置信区间以及构造等尾置信区间的依据。
均匀分布;置信区间;最大密度区间
1 问题的提出
均匀分布也称为平顶分布,是一种常见的连续型分布,也是在理论和实践中都有重要应用的一种概率统计模型。理论上,均匀分布在构造性地证明随机变量存在定理中起到关键作用[1];任何连续型随机变量X的分布函数F(x)对应的随机变量F(X)都服从区间(0,1)上的均匀分布[1]。生活和生产实际中也经常使用,比如:半径为r的汽车轮胎的圆周接触地面的位置X服从均匀分布U(0,2πr)[1],这从报废轮胎四周的磨损程度几乎相同可以得到印证。
一般均匀分布U(a,b)的参数估计是理论和实际应用中不可或缺的一部分,而区间估计是更是参数估计中的重要内容。在给定置信水平下构造的置信区间,人们关心的是该区间的精确度问题,而区间的精确度通常由两方面来衡量:一是置信区间的平均长度越短越好,二是置信区间包含真值的概率越大越好。在实际应用中,通常使用置信区间长度来衡量其精确度。因此研究各种分布参数的最短置信区间有一定的理论和现实意义。一般均匀分布U(a,b)的参数a和b的最短置信区间是统计文献中的常见的研究内容[2-5],都是和其他分布参数一样使用枢轴量和分布的分位数构造置信区间以及使用极值确定最短置信区间[6-8],但确定的依据却都没有明确提出.本文对形如U(0,1)和U(0,2πr)的简单均匀分布U(0,θ),利用数学分析中计算函数条件极值的方法得到参数q的最短同等置信区间,并用最大密度区间法[9]验证了该区间确实是给定置信水平下的最短置信区间,并由此印证最大密度区间正是确定参数最短置信区间以及构造等尾置信区间的依据。
2 U(0,θ)中参数θ的最短同等置信区间的求法
计算U(0,θ)中参数θ的最短同等置信区间,为了行文需要,给出如下概念:
定义2(同等置信区间):设θ是某总体的一个取值于Θ 的参数,x1,…,xn为抽自该总体的一个样本,对给定的a∈(0,1),若存在两个统计量与,且满足,使得∈Θ),则称随机区间为参数 q 的 1-a 同等置信区间。
定义3(最大密度区间):将随机变量的具有高密度值的点归入某个区间,使该区间外的点的密度值不超过区间内的任意点的密度值,若这种集最大密度点形成的区间存在,则称该区间为对应随机变量的最大密度区间,并且最大密度区间的长度是最短的。
对给定的a∈(0,1),U(0,θ)中参数θ的最短同等置信区间由下面定理给出:
定理:设x1,…,xn是来自均匀分布总体U(0,θ)的一个样本,对给定的α(0<α<1),参数θ的1-α最短同等置信区间为其中x(n)为该分布的最大次序统计量。
证明:第一步:构造枢轴量。
首先寻找参数θ的一个点估计,由于矩法估计精度不高,所以寻求θ的极大似然估计。
由于似然函数为:
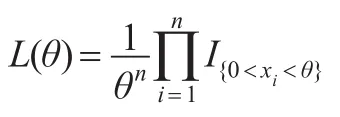
要使L(θ)达到最大,示性函数取值必须为1,其次是尽可能大,由于是θ的单调减函数,所以θ的取值应尽可能小,但示性函数为1决定了θ不能小于x(n),由此得到参数θ的极大似然估计为
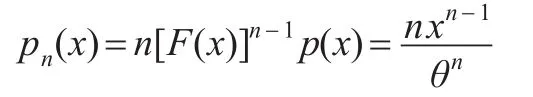
从而有G的概率密度函数为:
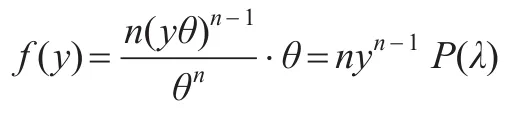
很明显它与参数θ无关,所以是枢轴量。
第二步:选择常数c和d,使得概率等式P(c≤G≤d)=1-α恒成立。

从而有:
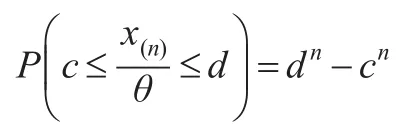
因此c和d满足dn-cn=1-α。
第三步:求参数θ的1-α同等置信区间。
第四步:寻找最短1-α同等置信区间。
由于0<c<d≤1,且dn-cn=1-α,所以求二元函数的极值问题就变成了限制条件φ(c,d)=dn-cn-1+α=0下的条件极值问题了。一般考虑使用数学分析中的拉格朗日乘数法求之,但是函数在区域E={(c,d):0<c<d≤1}的内部没有稳定点,自然也没有候选极值点,因此该函数如果存在极值点也只能在边界点处取得,但区域E的边界点有无穷多个,无法一一验证,所以尝试转用无条件极值借助函数的特性求之。
由于dn-cn=1-α,从而有于是有:
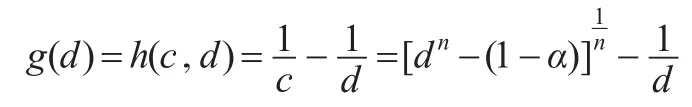
对函数g(d)是关于d求导,有:
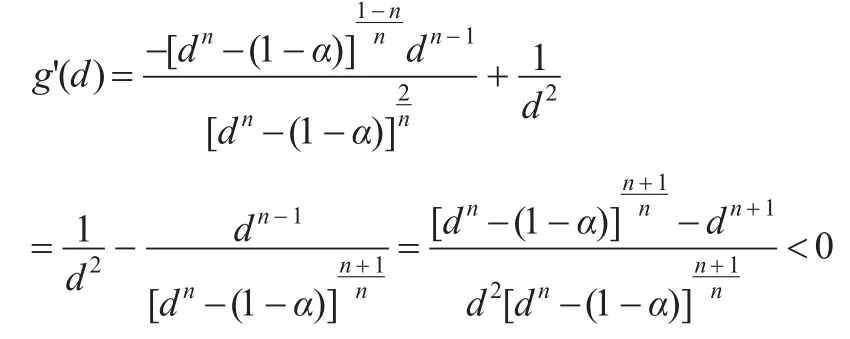
这说明g(d)是关于d的单调减函数,而0<d≤1,故g(d)在d=1处取得极小值,此时于是二元函数在点处取得最小值,因此参数θ的1-α同等最短置信区间为
这是从数学分析角度得到的最短置信区间,只是给出了计算方法,并没有指出构造最短置信区间的思想,而下面的从枢轴量的分布函数出发应用最大密度区间法,不但能确定参数的与前述相同的最短置信区间,而且还能体现出构造最短置信区间的指导思想。
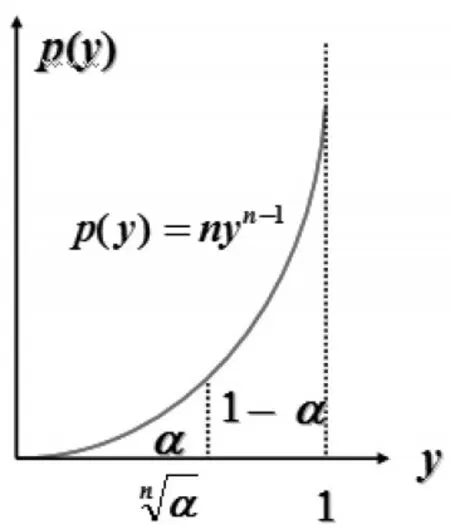
图1
3 结束语
本文对简单的均匀分布U(0,θ),分别运用函数极值和最大密度区间法计算了参数θ的1-α最短同等置信区间,两种方法得到的形式一致,其中最大密度区间法是一种比较巧妙的方法,它不但运用了数形结合的思想,还给出了利用分布的分位数构造最短置信区间的依据,该方法是构造参数的置信区间的指导思想。
[1]茆诗松,程依明,濮晓龙.概率论与数理统计教程(第二版)[M].北京:高等教育出版社,2011.
[2]王秀丽.均匀分布参数的最短置信区间[J].数学的实践与认识,2008,(5).
[3]曾艳.均匀分布参数的最短置信区间[J].赤峰学院学报:自然科学版,2011,(9).
[4]张红兵.均匀分布区间长度的最短置信区间[J].孝感学院学报,2007,(5).
[5]郑发美.两均匀分布区间长度比的置信区间与假设检验[J].统计与决策,2009,(22).
[6]徐付霞,董永杈,王娟.基于离散枢轴量的泊松分布参数的精确最短置信区[J].数学的实践与认识,2014,(24).
[7]徐美萍,于健,王若.威布尔分布中尺度参数的最短区间估计[J].江西师范大学学报:自然科学版,2015,(3).
[8]夏乐天,郭宝才,肖艳文.指数分布参数置信区间的最短化研究[J].河海大学学报:自然科学版,2003,(3).
[9]茆诗松,吕晓玲.数理统计学(第二版)[M].北京:中国人民大学出版社,2016.
(责任编辑/浩 天)
O212.1
A
1002-6487(2017)19-0084-03
吉林省社会科学基金资助项目(2014B137);吉林省科技发展计划项目(20150101007JC)
徐 宝(1977—),男,吉林四平人,博士,副教授,研究方向:数理统计。
