分层随机抽样条件下不同估计量的比较与选择

王春枝，赵国杰

（1.天津大学 管理与经济学部，天津 300072；2.内蒙古财经大学 统计与数学学院，呼和浩特 010070）

分层随机抽样条件下不同估计量的比较与选择

王春枝1,2，赵国杰1

（1.天津大学 管理与经济学部，天津 300072；2.内蒙古财经大学 统计与数学学院，呼和浩特 010070）

文章以分层随机抽样为例，研究了在有辅助变量可以利用的情形下，分别比估计、联合比估计、分别回归估计和联合回归估计的应用，并对其偏倚进行评估。结果表明，与简单估计相比，这类间接估计量都是非线性的较为复杂的估计量，可以改善简单估计的效果，且当目标变量和辅助变量高度相关时，各种估计量均是有效的。

分层随机抽样；比估计；回归估计；辅助变量

0 引言

抽样调查中，估计方法的设计是抽样设计的一个重要内容，对抽样误差有着直接的影响。调查中的目标量也即需通过样本估计的总体参数，常见的包括三种：总体均值、总体总量、总体比例，这三个总体参数一般都是针对总体的某一个指标，在参数估计时将该指标作为唯一的调查变量，所得到的参数估计量属于线性的简单估计量，这种简单估计只涉及所要估计的指标本身，完全不依赖其他的关于总体的辅助信息，估计量具有无偏性、一致性、极大似然性等优良性质。不过，当存在可利用的与调查变量高度相关的总体其他信息且这些信息质量较好时，如果能够充分利用这些信息无疑将显著提高抽样估计的精度。将可用来帮助调查变量估计的其他变量称为辅助变量，利用调查指标与辅助变量之间的相关关系，可以构造另一类间接估计量，即比估计量或回归估计量，与简单估计相比，这类间接估计量都是非线性的较为复杂的估计量，可以改善简单估计的效果。

本文以分层随机抽样为例，研究在有辅助变量可以利用的情形下，分别比估计、联合比估计、分别回归估计和联合回归估计的应用，并对其偏倚进行评估。

1 比率估计量与回归估计量

1．1 比率估计量及其性质

设总体有N个抽样单位，每个抽样单位有两个变量，调查变量Y和辅助变量X，记为总体比率。设从总体N中随机抽取容量为n的样本，以作为R的估计量，称R̂为比率估计量，其中大写记号代表总体变量，小写记号代表样本变量。

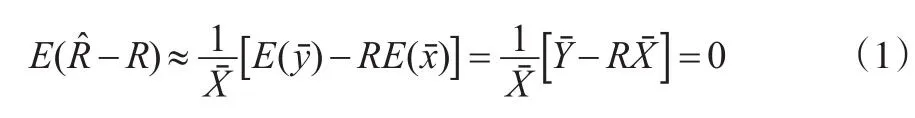
可见当n较大时，E(R̂)≈R，进而估计量的方差：

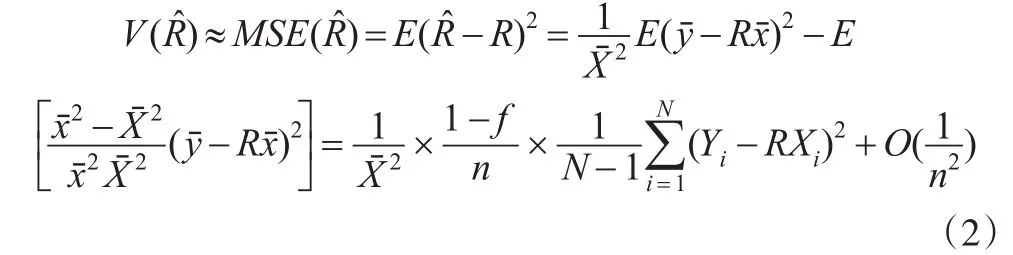
对每个总体单元，令Gi=Yi-RXi，i=1，2，...，N,则,因此：

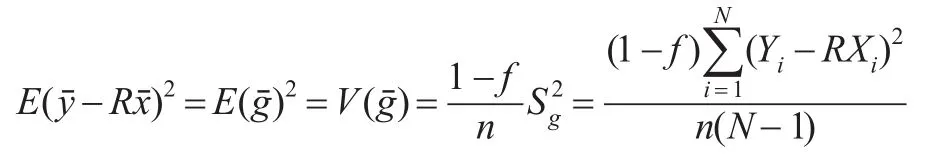
所以：

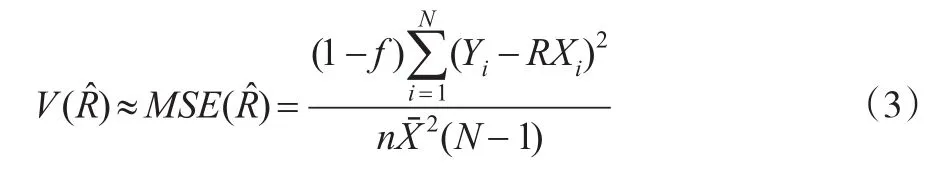
式（3）中涉及总体的，必须从样本中估计，可用作为的估计。这个估计是有偏的，由式（2），其偏倚的阶为，可见，均方误差与偏倚具有相同的阶，因此，比估计的偏倚趋于0的速度比相应的均方误差的平方根趋于0的速度更快，比率估计量虽然是有偏的，但当样本容量较大时，偏倚趋于0。进一步，用比率估计量估计总体均值，得到：

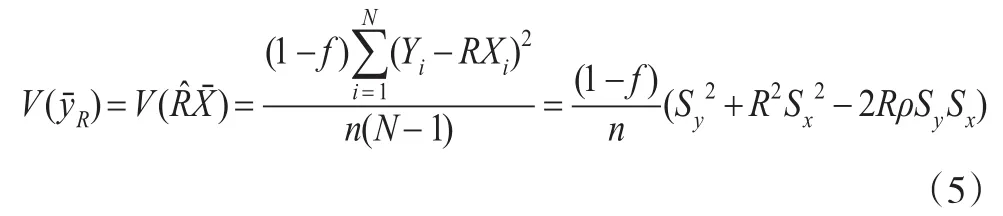
上式中，、、ρ分别为调查变量样本方差、辅助变量样本方差和调查变量与辅助变量的样本相关系数，Sy、Sx为相应的标准差。

利用比估计方法时，调查变量与辅助变量间需有正线性相关关系，且大致呈正比例，如果辅助变量与调查变量间有负线性相关关系，则要采取乘积估计。估计，一般要求辅助变量的总体总量或均值是已知的；比估计方法适用面广,可以用于简单随机抽样,也可用于分层随机抽样、整群抽样、多阶抽样等。由于比估计充分利用了辅助变量带来的信息估计总体参数，比单纯用调查变量资料会有更好的效果。

1．2 回归估计量及其性质

有效地应用比估计隐含的一个基本假定是调查变量与辅助变量基本成比例关系，也就意味着调查变量对辅助变量的回归直线通过原点，若此假定不成立，为了进一步提高估计精度，可以使用回归估计。一般地，对于简单随机抽样，总体均值的回归估计量定义为：

β可以是事先设定的常数，也可以是从样本中计算得到的样本回归系数。如果事先给定，β=β0，回归估计量的方差为：

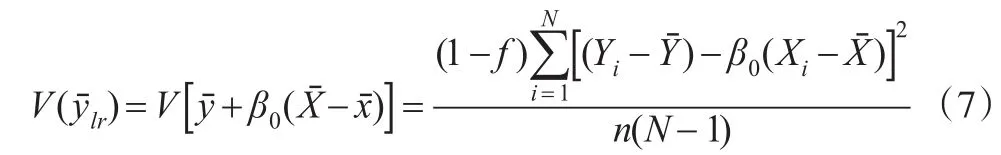
此时，是总体均值的无偏估计量。如果β为样本回归系数，则，此时回归估计量的方差为：

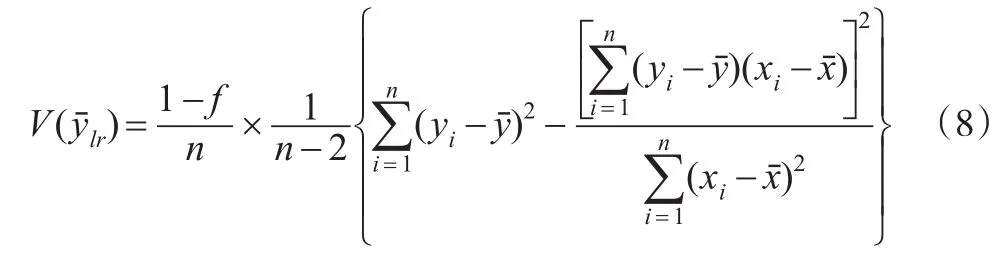
此种情形下，当样本容量n较大时，是近似无偏的；当n趋于无穷大时，的偏倚趋于0的速度比相应的均方误差的平方根趋于0的速度更快，回归估计量仍是可用估计量。

同比估计一样，回归估计充分利用了有关的辅助变量资料以有效地提高估计的精度，当然，回归估计量的优越性只有在大样本的情形下才能得到较好的发挥。此外，回归估计中辅助变量可以是一个，也可以是两个或多个。

2 分层随机抽样中估计量的构造

将比估计与回归估计的思想应用于分层随机抽样中，根据应用的场合不同，有两种可行的方法。一种是对每层的样本考虑比估计或回归估计，然后根据层权进行加权处理；另一种是对调查变量和辅助变量先进行总体的参数估计，然后用他们构造比估计量或回归估计量。

2．1 分别比估计和分别回归估计

各层分别比估计是先对各层分别进行比估计，然后按层权加权平均，以得出总体参数的估计，设总体分为L层，和ˉh为第h层的样本均值，ˉh和ˉh为第h层的总体均值，Wh为层权，则总体均值的比估计为：

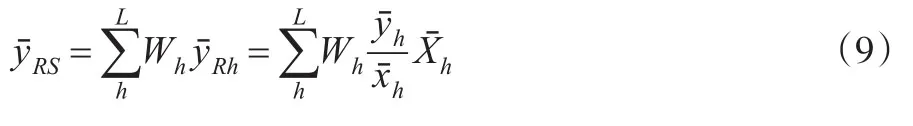
由于当每一层的样本容量nh都比较大时，是近似无偏的，因此，此时也是近似无偏的，且从每一层比估计的方差公式可以得到：

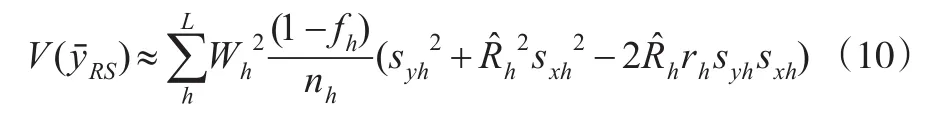
与分层比估计的情形一样，先在每层中对层的均值作回归估计，然后再加权，即可得到分别回归估计量

其中βh为第h层事先设定的值或样本回归系数，当βh为事先设定的值时，分别回归估计量的方差为：；若βh为样本回归系数，则估计量的方差为：。前者为无偏估计量，后者则是有偏估计量。

2．2 联合比估计和联合回归估计

对于第h层的总体均值，先对各层的调查变量与辅助变量进行分层随机抽样的简单估计，进而利用比率估计量可以构造出联合比估计量：

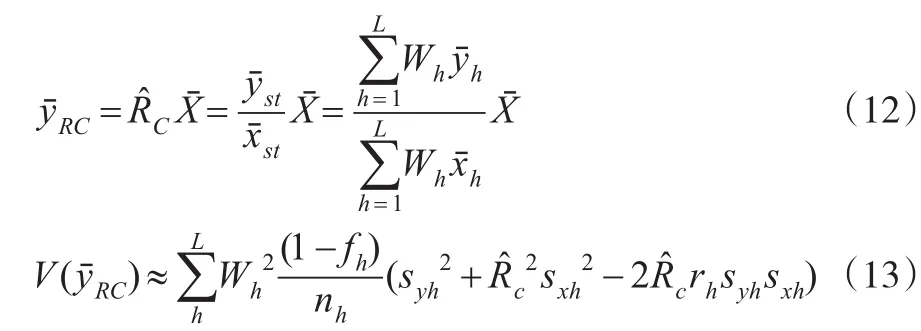
基于同样的思想，联合回归估计为：

当β为事先设定时，估计量是无偏的，并且：

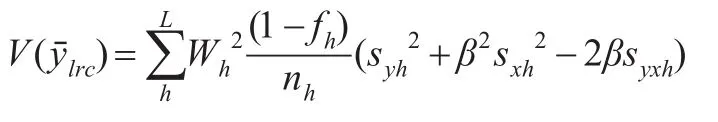
当β必须从样本估计时，一般采用按比例分配的抽样方法得到β的估计值，，通常称为联合最小二乘估计。此时联合回归估计是有偏的，但满足渐进一致性，估计量的方差为：

3 不同估计量的比较与选择

3．1 分别比估计与联合比估计

分层随机抽样条件下，分别比估计和联合比估计均为有偏估计量，当各层的样本容量足够大时近似无偏，当某些层的样本量不够大，而总样本量较大时，联合比估计近似无偏。比较二者的方差，式（13）减去式（10）可得：

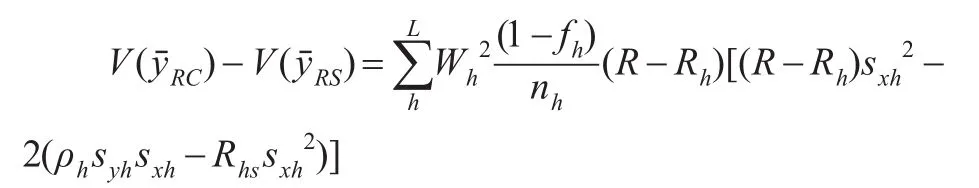
（1）当R=Rh或者，每一层的总体比值都严格地等于整个总体的比值，此时，分别比估计与联合比估计的精度是一样的。

（2）当R≠Rh，而，则时，即Rh等于第h层Y对X的线性回归函数，此时，，此时，分别比估计的精度至少和联合比估计一样甚至更高。这意味着分别比估计由于联合比估计有两个前提条件：一是调查变量与辅助变量存在显著的线性相关关系，这个前提对任何比估计都是成立的；二是各层的样本容量都比较大，此时分别比估计要优于联合比估计，否则，若一些层的样本容量不足，分别比估计的偏倚会较大，而联合比估计的精度会更高一些。

3．2 分别回归估计与联合回归估计

在回归估计中，多数情况下，回归系数需要利用样本回归系数进行估计，属于有偏估计量，只有在大样本情况下，才会渐进无偏。少数情况下，当回归系数事先设定时，估计量是无偏的。比较分别回归估计和联合回归估计的方差：

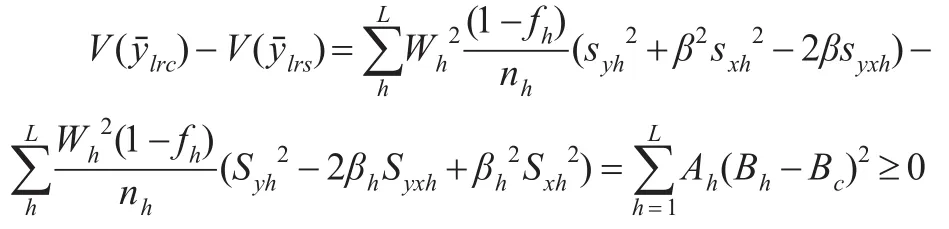
4 结论

利用辅助信息进行分层随机抽样，在样本的代表性方面提高了抽样效率，这是分层随机抽样自身所具有的优越性。当利用这种优越性得到样本后，需要对总体的参数进行估计，利用辅助变量构建分别比估计量、联合比估计量、分别回归估计量、联合回归估计量均能够有效地改善简单估计的精度，其中回归估计中的回归系数可以是事先设定的常数，也可以是从样本得到的估计值。在大样本的条件下，且辅助变量与目标变量相关性有较高时，比估计量和回归估计量近似无偏且有效。在实际情况中，通常能够获得历史资料或者与要研究问题高度相关的辅助量的资料，利用这些辅助资料，有助于做出更科学的估计。

事实上，在分层随机抽样条件下，对于辅助变量的利用实际上存在两个角度，分别比估计量、联合比估计量、分别回归估计量、联合回归估计量是将辅助变量的信息利用于参数估计过程中。在实践中，辅助变量的信息还被作为分层标志应用于对抽样总体的分层，进而采取简单估计。考虑样本容量以及目标变量与辅助变量相关程度的不同，这两种利用辅助变量信息的方法，在估计效果上会存在差异，哪一种利用方法效果更好？这是值得进一步研究的问题。

［1］金勇进，杜子芳，蒋妍.抽样技术［M］.北京：中国人民大学出版社，2008.

［2］赵俊康.统计调查中的抽样设计理论与方法［M］.北京：中国统计出版社，2002.

［3］冯士雍,倪加勋,邹国华.抽样调查理论与方法［M］.北京：中国统计出版社，1998.

［4］刘琴,汤银才.分层随机抽样中R的分别比估计量的可用性及其均方误差的估计量［C］.中国现场统计研究会学术年会论文集，2005.

［5］罗钰莹.分层抽样下提高估计精度的探究［J］.港澳经济,2016,(23).

［6］陈兵,吕恕.有辅助信息可利用时的分层抽样下样本轮换研究［J］.统计与决策，2014,(15).

（责任编辑/亦 民）

Comparison and Selection of Different Estimators Under Stratified Random Sampling

Wang Chunzhi1，2，Zhao Guojie1
(1.Department of Management and Economics，Tianjin University，Tianjin 300072，China;2.School of Statistics and Mathematics，Inner Mongolia Finance and Economics University，Hohhot 010070，China)

This paper takes stratified random sampling as an example to study the application of separate ratio estimator,combined ratio estimator,separate regression estimator and the combined regression estimator under the condition that the auxiliary variable is available,and on this basis assesses the bias of the estimators.The study result shows that compared with the simple estimation method,such indirect estimators are complex nonlinear estimators,and can improve the accuracy of simple estimation method;when the target variable is highly correlated with the auxiliary variable,all estimators are valid.

stratified random sampling;ratio estimation;regression estimation;auxiliary variable

0212

A

1002-6487（2017）19-0015-03

内蒙古自然科学基金资助项目（2014MS0701）

王春枝（1976—），女，内蒙古巴彦淖尔人，博士研究生，副教授，研究方向：技术经济及管理。

赵国杰（1950—），男，河北保定人，教授，博士生导师，研究方向：技术经济及管理。