湖北碳市场价格形成机制及价格预测

姚 奕，吕 静,b，章成果

（南京师范大学a.数学科学学院;b.计算机科学与技术学院,南京 210023）

湖北碳市场价格形成机制及价格预测

姚 奕a，吕 静a,b，章成果a

（南京师范大学a.数学科学学院;b.计算机科学与技术学院,南京 210023）

文章通过EMD-SVM模型考察湖北碳市场碳价格形成机制并进行碳价格预测。结果表明：碳市场供需不均衡和碳市场发展过程中的重大事件对碳价格产生了较大的影响；同时，EMD-SVM模型也被证实具备良好的预测能力，期望能为市场决策者和参与者提供碳资产管理和风险规避保证。

碳价格；形成机制；预测；EMD-SVM模型

0 引言

随着全球经济高速发展，环境及能源问题日渐突出，其中温室效应严重威胁人类的可持续发展。历史经验表明，仅依靠强制性减排要求或经济主体的自愿性减排很难达到减排目标。二氧化碳排放权交易市场是通过市场经济获得低成本减排的有效手段，是减少温室气体排放量、提高能源利用效率、应对全球气候变化的有效途径。为了取得试点经验，摸索碳市场发展路径，现阶段中国试点碳市场的运行状态备受各界关注。厘清碳价格的形成机制有益于制定碳排放权交易市场政策，有利于建立全国统一的碳排放权市场，有效的碳价预测可以为市场参与者提高碳市场风险防范能力和减少碳资产价值流失提供保障。

国内外学者们对欧盟碳交易价格形成机制的研究较为丰富，研究者们普遍认为经济活动、金融市场、制度设计、能源价格等深刻地影响着欧盟碳排放权价格[1-8]。对国际碳市场碳价格预测多基于经典的时间序列分析方法、数据挖掘技术以及相关的混合模型[9-14]。然而，针对国内试点碳市场价格进行实证分析并进行预测的研究并不丰富。事实上，一方面，由于中国碳市场运行时间不长，碳市场价格数据量有限，无法匹配一些可能的价格驱动因素的年度数据，如产业结构、经济发展水平、天气原因、人口规模等；另一方面，对发展尚不成熟的中国碳市场无法建立有效的计量模型。基于此，本文选择EMD模型克服以上问题，以湖北碳价格日数据为基础，通过EMD-SVM模型考察湖北碳市场在一个完整的履约期内其价格形成机制，并对碳价格进行预测，以期对中国碳交易试点市场监管层、投资者和参与主体提供有价值的参考。

1 研究方法

1．1 EMD算法

经验模态分解（EMD）[15]算法从数据本身特性出发，将原信号中不同尺度的波动和趋势逐级分解，生成一系列本征模函数（IMF)，以揭示数据波动的内在规律。分解出的IMF具有如下特征：（1）极值点的数量与过零点的数量最多相差一个；（2）在任意时刻，其上、下包络线的均值为0。

设碳价格序列为xt，EMD算法如下：

步骤1：确定序列x(t)的极值点，利用三次样条插值函数分别由极大值点、极小值点形成上包络线eup(t)和下包络线elow(t)；

步骤2：计算包络均值m(t)，m(t)=(eup(t)+elow(t))/2；

步骤3：计算新序列c(t)，c(t)=x(t)-m(t)；

步骤4：若c(t)满足IMF的两个特征，则c(t)是一个IMF，用r(t)=x(t)-c(t)代替步骤1中的x(t)；若c(t)不是一个IMF，则用c(t)代替步骤1中的x(t)；

步骤5：重复步骤1至步骤4，直到c(t)成为一个IMF，记作c1(t)。重复算法，直到rn(t)只有一个极值点或是一个单调函数。

1．2 fine-to-coarse reconstruction算法

碳价格序列x(t)通过EMD算法分解得到m个IMF和1个趋势项，其算法步骤如下：

步骤1：计算从c1(t)到ci(t)的叠加和序列的均值；

步骤2：选取显著性水平α，利用t检验判别si中均值距离显著不为0的ci(t)；

步骤3：从c1(t)到ci-1(t)相加重构为高频分量，ci(t)到cn(t)相加构成了低频分量。

1．3 支持向量机(SVM)

SVM是由Cortes和Vapnik[16]提出的基于统计学习理论的机器学习方法，具有学习速度快、全局性、泛化性能好等特点。其基本思想是把输入向量通过非线性映射φ(x)映射到高维特征空间，并在特征空间中进行线性回归，回归函数为：

其中，ω是权向量，b是偏置向量，通过正则化和结构风险准则估计。

根据结构风险最小化准则可转化为如下最优化问题：

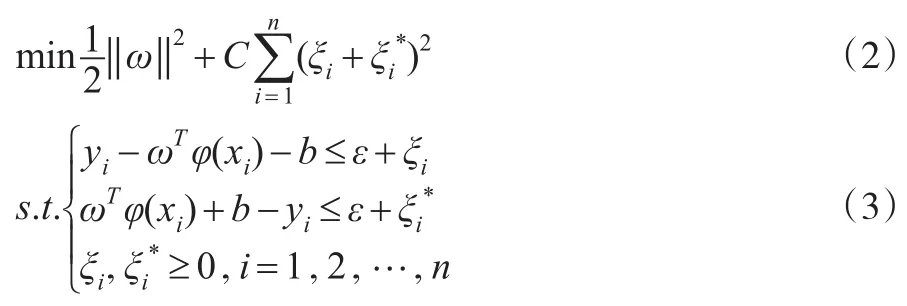
其中，ξi、为松弛变量，C为惩罚因子，ε是不敏感损失系数，n为样本容量。利用拉格朗日函数法求这个约束优化问题，得到SVM回归函数：

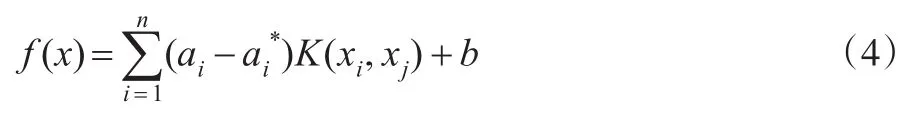
其中，ai、是拉格朗日乘子，K(xi，xj)是核函数。

1．4 EMD-SVM模型

步骤1：对碳价格进行EMD分解，得到若干个IMF和1个趋势项，并重构为高频、低频分量和趋势项；

步骤2：对高频、低频分量和趋势项三个序列进行SVM预测；

步骤3：将各序列的预测值重新组合得到碳价预测值。

2 实证分析

本文选取湖北碳市场2014年4月2日至2015年11月20日的日价格，其中已经包含了一个履约期，除去节假日等因素，取得401组数据（数据来源于中国碳排放交易网）。本文采用MATLAB和SPSS软件进行数据处理。

2．1 碳价格EMD分解

湖北碳市场碳价格经过EMD分解得到7个IMF和1个趋势项，分解结果如图1所示。

图1中的IMF按照频率从高到低排列为IMF1—IMF7，它们展示了碳价变化的频率和振幅随时间的变化，随着频率的降低，振幅也相应增加。

2．2 IMF特征分析

本文利用IMF平均周期、方差占比、IMF与原价格序列的Pearson相关系数和Kendall相关系数等指标分析IMF和趋势项的特征和意义，结果见表1。

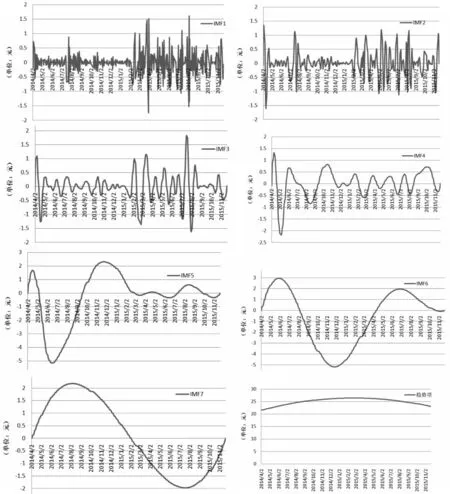
图1 湖北碳价格的EMD分解结果

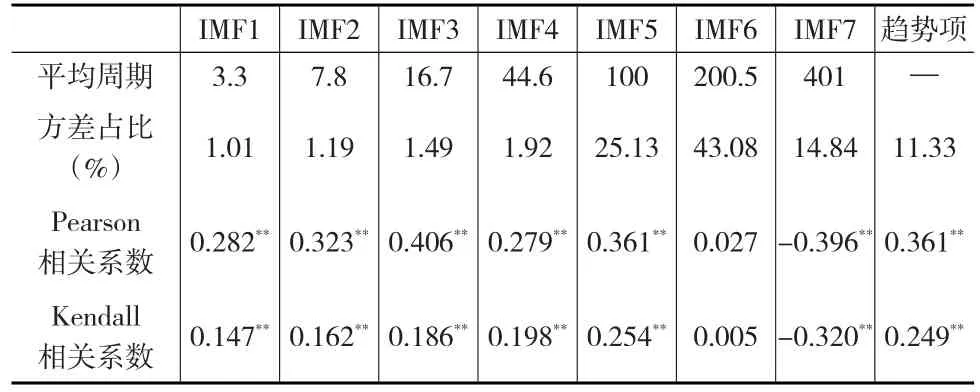
表1 IMF和趋势项的统计指标

IMF1—IMF4周期较短，分别为3天、8天、17天和45天，均不超过45天，其Pearson相关系数和Kendall相关系数都在0.01水平上显著，表明周期为3天、8天、17天和45天的价格影响因素均对湖北碳价格的形成产生显著影响；其方差占比均不大，说明周期较短的价格影响因素对碳价格波动的贡献较小。

IMF5—IMF7周期较长，分别为100天、201天和401天，均超过了100天，其中除了IMF6之外，IMF5和IMF7的Pearson相关系数和Kendall相关系数都在0.01水平上显著，数值较IMF1—IMF4整体偏大，且其方差占比远大于IMF1—IMF4的方差占比，说明较长周期的价格影响因素对湖北碳价格波动的贡献更大。

趋势项的Pearson相关系数和Kendall相关系数都在0.01水平上显著，方差占比为11%，趋势项对湖北碳价格的形成作用显著。

2．3 碳价格结构影响因素分析

根据fine-to-coarse reconstruction算法将湖北碳价格序列分解后的模态进行重构，对组合而成的高频分量、低频分量以及趋势项进行分析。计算si（i=1,2,…,7)均值的t检验值（显著性水平α=0.05），下页表2的检验结果表明，t检验值在i=5处距离0开始显著，由此，IMF1—IMF4叠加代表了高频分量，IMF5—IMF7叠加代表了低频分量，其相关统计指标列于表3。湖北碳价格及其高频分量、低频分量和

趋势项的分解如图2所示。

表2 si均值和t检验值

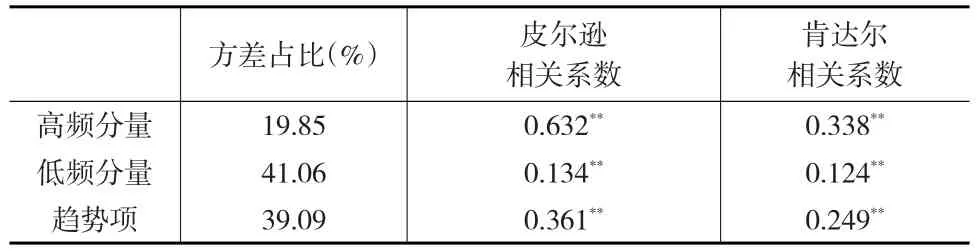
表3 高频、低频分量和趋势项的统计指标

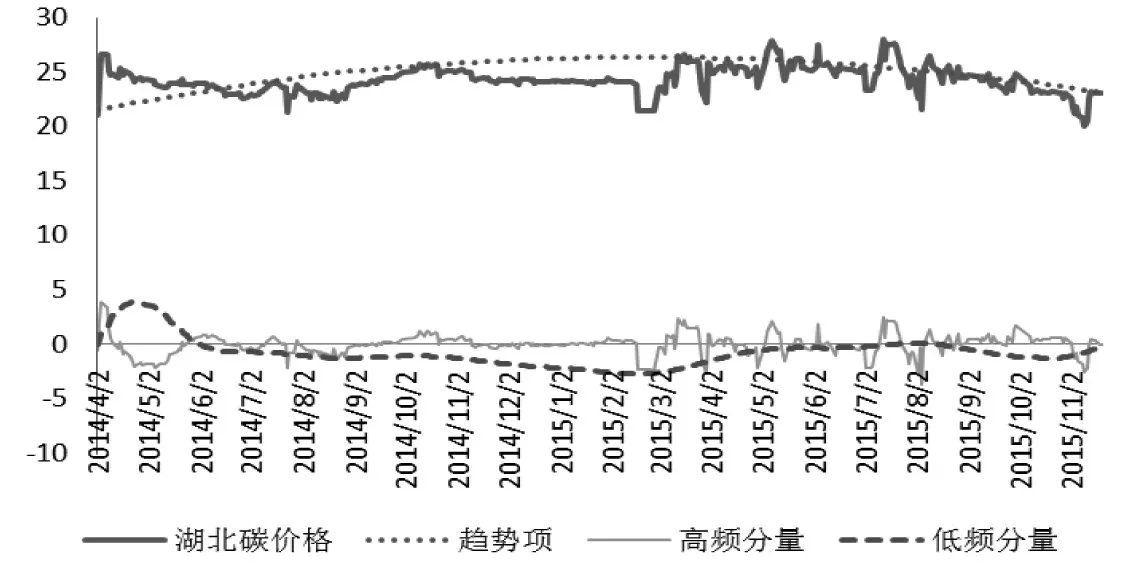
图2 湖北碳价格高频分量、低频分量及趋势项

比较表1和表3所列结果，高频分量的相关系数较重构之前有了明显提高，相关性增强，对碳价形成贡献更大。低频分量和趋势项的方差占比也均在40%左右，对碳价格波动性的解释能力增强。由此，对碳价格影响因素的结构优化，改善了碳价形成机制分析的准确性。

2.3.1 高频分量（IMF1—IMF4）：市场短期供需不均衡和市场随机效应影响

碳市场具有一般市场属性，受到市场供需状况的影响，而市场供需受到能源价格、投机行为、天气、突发的政治局势等因素的影响。这些因素的影响往往持续时间短，体现在高频分量中。对高频分量的分析有助于理解碳市场发展过程中市场短期供需不均衡和市场随机效应对碳价格的影响。

高频分量的Pearson相关系数和Kendall相关系数分别为0.632和0.338，说明高频分量与碳价格存在着较强的相关关系，市场短期供需不均衡对碳价的形成贡献较大，图2中也显示了高频分量与原价格序列相似程度高，具有较一致的变化趋势。

履约是碳市场运行的重要节点，履约期前后，碳市场的交易量和交易价格均会呈现出较大的波动。在2015年7月前后，高频序列波动较其他时间段更大。6月份，高频分量基本在0均值附近波动，碳市场受到正常的短期供需不均衡影响；7月份，高频分量逐渐正向上升，并达到了峰值2.58元/吨，市场活跃，供不应求；随着履约期临近，履约单位通过交易获取了配额，到了8月初，高频分量大幅减少至0均值以下；履约完成后，高频分量波动减弱，在0均值附近波动。对未来碳市场和配额等因素的不确定，导致了市场投机现象的存在，碳价格在短期内较大的变动。湖北碳市场履约期的碳价格变化为履约期碳市场平稳过度提供了参考。

2.3.2 低频分量（IMF5—IMF7）：重大事件影响

重大事件对碳价格的影响体现在低频分量中，这样的异质性环境对碳价格的影响较大，持续时间长，幅度大，而频率较低。对低频分量的分析有助于理解碳市场发展过程中重大事件对碳价格的影响。

从IMF5—IMF7的周期来看，均超过100天，重大事件的影响持续时间长，影响很难消除，且振幅较大，对碳价格波动的影响程度大。低频分量的Pearson相关系数和Kendall相关系数分别为0.134和0.124，说明低频分量与碳价格存在着显著的相关关系，在数值上明显小于高频分量对应的数值，重大事件对碳价格形成影响较弱。然而，低频分量对碳价格变化的解释度为41%，表明重大事件在一定程度上解释了湖北碳价格的波动。

由于湖北碳市场交易时间不长，且试点市场尚处于摸索阶段，碳价格易受到如新制度、配额分配等重大事件的影响。2014年9月9日，湖北碳市场推出国内第一单碳资产质押贷款融资业务，之后的一个多月时间内，低频分量缓慢上行；2015年3月6日，湖北碳市场首次履约动员暨核查工作启动会召开后，低频分量大幅上行；2015年6月中旬，国家外汇管理局正式同意合格境外投资者可以参与湖北碳市场交易，意味着合格境外投资者可以外汇或跨境人民币参与湖北碳排放权交易，低频分量又出现持续上行。因此，市场参与者应关注重大事件的发生，并根据其性质判断碳价走势。

2.3.3 趋势项：潜在运行规律

趋势项反映了碳价格演化的长期趋势，是碳市场制度因素对碳价格影响的体现，可以为碳价格的预测提供有价值的参考。图2中湖北碳价格出现了先增后降的状态，运行较为平稳，碳价格未出现较大波动。趋势项基本上反映着碳价格演化的趋势，碳价格始终围绕着趋势项小幅波动。趋势项方差占比为39%，由此，趋势项较好地体现了碳价格平稳的长期趋势，较充分地解释了碳价格的波动。

2．4 价格预测

根据SVM分别对高频、低频分量和趋势项进行预测，采用RBF核，预测误差如表4所示。

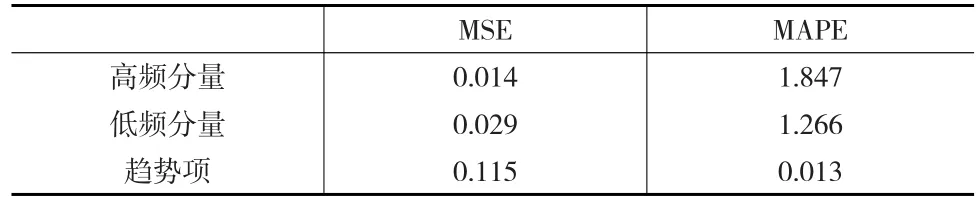
表4 分项预测误差

表4预测结果表明，EMD-SVM模型预测能力较强，尤其是趋势项的预测能力出色，反映出趋势项较好地把握碳价格演化的趋势，描述着碳价格的长期走势。

为了比较预测效果，本文还采用了SVM模型和AR(2)模型进行预测，预测误差如表5所示。

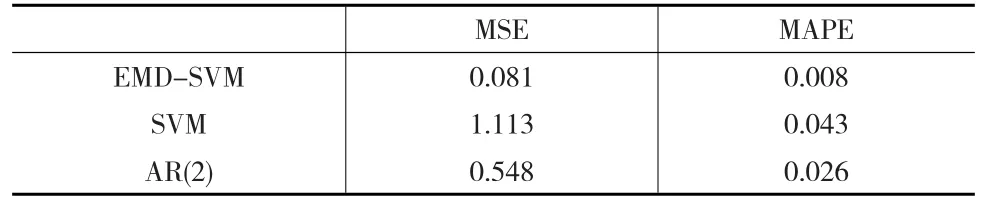
表5 预测误差比较

各预测方法的误差结果反映出EMD-SVM模型的预测效果明显优于SVM模型和AR(2)模型。由于EMD-SVM模型把碳价分解为高频、低频分量和趋势项后对各项进行预测再组合，有利于减少预测过程中的误差累积，从而提高了预测的精度，具有较优的预测能力。

3 结论

本文利用EMD模型将湖北碳价格重构为高频、低频分量和趋势项，以剖析碳价格形成机制，描述不同经济含义对碳价格的影响。高频分量代表了市场供需不均衡和随机效应对碳价格的影响因素，其与原碳价格存在着较强的相关关系，短期的市场波动造成的价格变化与碳价格变化一致，表明了市场供需不均衡对湖北碳价格产生了较大的影响；低频分量体现了重大事件对碳价格的影响，碳市场发展的重大事件解释了碳价的波动；趋势项反映了碳价格演化的长期趋势，是碳市场制度因素对碳价格影响的体现，湖北碳价格运行稳定，碳价格围绕趋势项小幅波动，趋势项基本反映碳价格的走势，可以为碳价格的预测提供有可靠的参考。此外，对分解得到的高频、低频分量和趋势项序列采用SVM进行预测，能减少预测误差，提高碳价格预测精度。

［1］Alberola E,Chevallier J,Cheze B.Price Drivers and Structural Breaks in European Carbon Prices 2005—2007［J］.Energy Policy,2008,(36).

［2］Hintermann B.Allowance Price Drivers in the First Phase of the EU ETS［J］.Journal of Environmental Economics and Management,2010,(59).

［3］Creti A,Jouvet P A,Mignon V.Carbon Price Drivers:Phase I Versus Phase Ii Equilibrium?［J］.Energy Economics,2012,(34).

［4］朱帮助,王平,魏一鸣.基于EMD的碳市场价格影响因素多尺度分析［J］.经济学动态,2012,（6）.

［5］Hammoudeh S,Nguyen D K,Sousa R M.What Explain the Short-term Dynamics of the Prices of CO2Emissions?［J］.Energy Economics,2014,(46).

［6］朱帮助.国际碳市场价格驱动力研究——以欧盟排放交易体系为例［J］.北京理工大学学报：社会科学版,2014,16（3）.

［7］Koch N,Fuss S,Grosjean G,et al.Causes of the EU ETS Price Drop:Recession,Cdm,Renewable Policies or a Bit of Everything?——New Evidence［J］.Energy Policy,2014,(73).

［8］王军锋,张静雯,刘鑫.碳排放权交易市场碳配额价格关联机制研究——基于计量模型的关联分析［J］.中国人口·资源与环境,2014,24（1）.

［9］Chevallier J.Volatility Forecasting of Carbon Prices Using Factor Models［J］.Economics Bulletin,2010,30(2).

［10］Byun S J,Cho H J.Forecasting Carbon Futures Volatility Using GARCH Models With Energy Volatilities［J］.Energy Economics,2013,(40).

［11］Martos C G,Rodriguez J,Sanchez M J.Modeling and Forecasting Fossil Fuels,CO2and Electricity Prices and Their Volatilities［J］.Applied Energy,2013,(101).

［12］朱帮助，魏一鸣.基于GMDH-PSO-LSSVM的国际碳市场价格预测［J］.系统工程理论与实践,2011,31（12）.

［13］Zhu B Z,Wei Y M.Carbon Price Forecasting With a Novel Hybrid ARIMA and Least Squares Support Vector Machines Methodology［J］.Omega,2013,(41).

［14］高杨,李健.基于EMD-PSO-SVM误差校正模型的国际碳金融市场价格预测［J］.中国人口·资源与环境,2014,24（6）.

［15］Huang N E,Shen Z,Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis［C］.The Royal Society A:Mathematical,Physical&Engineering Sciences:1998,(73).

［16］Cortes C,Vapnik V.Support-vector Networks［J］.Machine Learning,1995,20(3).

（责任编辑/刘柳青）

F206

A

1002-6487（2017）19-0166-04

中国博士后基金资助项目（2013M541697）；江苏省高校哲学社会科学基金资助项目（2013SJD790031）；江苏省博士后基金资助项目（1302044C）

姚 奕（1976—），女，江苏宜兴人，博士，副教授，研究方向：能源软科学。

（通讯作者）吕 静（1978—），女，江苏宜兴人，博士研究生，讲师，研究方向：机器学习。