2017年高考立体几何试题分析及备考建议

深圳中学(518025) 刘锋

2017年高考立体几何试题分析及备考建议

深圳中学(518025) 刘锋

本文通过对2017年广东省高考数学立体几何部分的试题分析及评卷总结,并且整理出近三年新课标卷对立体几何部分的考查情况,揭示其命题特点.据此,文末给出高三数学在立体几何部分的复习备考建议,以期对一线教师有所裨益.

立体几何新课标卷空间角空间想象能力

一、2017年新课标I卷高考数学立体几何试题主观题分析

笔者今年有幸参加2017年广东省高考数学评卷工作,作为总结,下面介绍立体几何主观题,考生的典型解法及评卷过程中发现的典型错误与错因分析,以期对2018届高考数学备考有一些启示.

真题1(文科第16题)已知三棱锥S−ABC的所有顶点都在球O的球面上,SC是球O的直径,若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S−ABC的体积为9,则球O的表面积为.

解析 由SA=AC,得OA⊥SC,由平面SCA⊥平面SCB,得OA⊥平面SCB,即OA为三棱锥S−ABC的高.又SC是球O的直径,且SB=BC,所以△SBC是等腰直角三角形.记球O的半径为R,则三棱锥S−ABC的体积

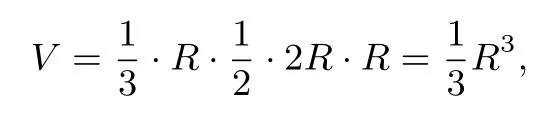
此题的典型错误主要有4π,6π,12π,16π,错因主要是考生的空间想象能力偏弱,未弄明白三棱锥S−ABC与球O的位置关系,导致球的半径求错或求不出来.

真题2(理科第16题)如图1,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O,D,E,F为圆O上的点,△ECA,△FAB,分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DCB,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为.

图1

图2

解析 如图2,连接OD交BC于G,由题意得OD⊥BC.设等边三角形ABC的边长为x,又O为中心,则

解法一(利用均值不等式)

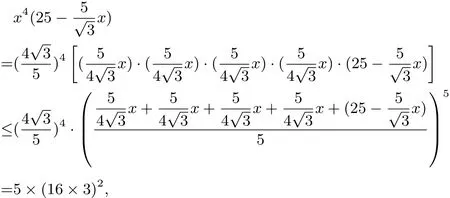
解法二(利用导数) 对f(x)求导并化简得f′(x)=当x变化时,f(x),f′(x)变化情况列表如下:

x (0,4√3)4√3(4√3,5√3)f′(x)+0−f(x)↗极大值↘

真题3(文科第18题)如图3,在四棱锥P−ABCD中,AB//CD,且 ∠BAP= ∠CDP=90°.

(1)证明:平面PAB⊥平面PAD;

(2)若 PA=PD=AB=DC,∠APD=90°,且四棱锥P−ABCD的体积为求该四棱锥的侧面积.

图3

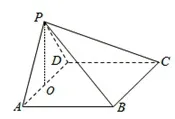
图4

解析 (1)由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.由于AB//CD,故AB⊥PD,从而AB ⊥平面PAD.又AB⊂平面PAB,所以平面PAB⊥平面PAD.

(2)解法一 如图4,在平面PAD内作PO⊥AD,垂足为O.由(1)知,AB⊥平面PAD,故AB⊥PO,可得PO⊥平面ABCD.因为AD ⊂面PAD,所以AB⊥AD.又因为AB//CD,且AB=CD,所以,四边形ABCD为矩形.故四棱锥P−ABCD的体积

可见,△PBC是等边三角形.所以,四棱锥P−ABCD的侧面积为

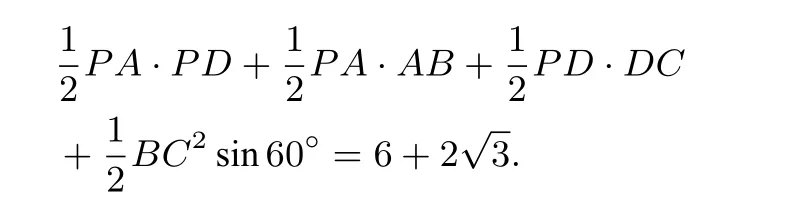
解法二 由题意知,AB//CD 且 AB=CD,所以四边形ABCD为平行四边形.由(1)知,AB⊥平面PAD,AD ⊂平面PAD,所 以 AB⊥AD,即四 边 形ABCD为矩形.又AB⊂平面ABCD,则平面ABCD⊥平面PAD.如图5,取AD中点O,连结PO,因为PA=PD,所以PO⊥AD,平面ABCD∩平面PAD=AD,PO⊂平面PAD,则PO⊥平面ABCD,余下同解法一,从略.

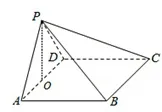
图5

解法三 由题意知,AB//CD 且 AB=CD,所以四边形ABCD为平行四边形.如图6，取AD中点E,连结PE,取BC中点F,连结FE,FP,则四边形ABFE为平行四边形.因为PA=PD,所以PE⊥AD.由(1)知,AB⊥平面PAD,AD⊂平面PAD,所以AB⊥AD,即四边形ABCD为矩形.

图6

解法四 AB//CD且AB=CD,所以四边形ABCD为平行四边形.所以 VP−ABCD=2VP−ABD.由(1)知,

AB⊥平面PAD,所以,

真题4(理科第18题)如图7,在四棱锥P−ABCD中,AB//CD,且 ∠BAP=∠CDP=90°.

(1)证明:平面PAB⊥平面PAD;

(2)若 PA=PD=AB=DC,∠APD=90°,求二面角A−PB=C的余弦值.

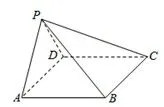
图7

解析 第(1)问同文科,略.

(2)解法一(向量法) 在平面PAD内作PF⊥AD,垂足为F,由(1)可知,AB⊥平面 PAD,故 AB⊥PF,可得PF⊥平面ABCD.如图8,以F为坐标原点,的方向为x轴正方向,为单位长,建立如图所示的空间直角坐标系F−xyz.

图8

由(1)及已知可得

设m=(x1,y1,z1)是平面PAB的法向量,则

解法二(定义法)如图9,取PB中点E,连接AE,CE,AC.由(1)知AB⊥面PAD,所以AB⊥AD,AB⊥PA.不妨设 AB=1,则PA=PD=AB=DC=1.在Rt△PAB中,AB=PA=1,则

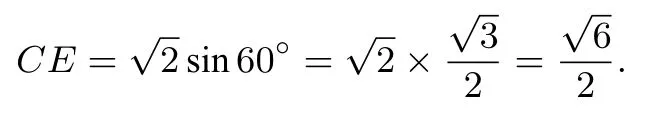
由二面角的平面角的定义知∠AEC为二面角A−PB−C的平面角.在△AEC中,

图9

关于考生的典型错误及错因分析请参见参考文献[3].

二、近三年新课标卷对立体几何的考查情况及特点

(一)文科

新课标I 新课标II 新课标III题 号考查内容难度题 号考查内容难度题 号考查内容难度6(∗)圆锥的体积计算易6(∗)三视图易2015 11(∗)三视图中10(∗)三棱锥的外接球易18垂直关系及三棱锥的体积侧面积计算中19长方体中的截面问题及多面体的体积中7(∗)三视图易4正方体的外接球易10(∗)三视图易2016 11(∗)异 面 直 线的夹角中7(∗)三视图易11(∗)三棱柱的内切球易18垂直关系及三棱锥的体积难19垂直关系及五棱锥的体积中19平行关系及四面体的体积中6平行关系易6(∗)三视图易9(∗)圆柱易2017 16三棱锥的外接球中15长方体的外接球易10垂直关系中18垂直关系及四棱锥的体积与侧面积中18平行关系及四棱锥的体积中19垂直关系及四面体的体积n难

(二)理科

注:文科标注(∗)的题目为同一套试卷,文理科考查相同的题目.

从上述表格,笔者总结出新课标卷对立体几何部分的考查有如下特点:

1.考查的题量(分值)、形式、内容及难度等非常稳定,具有“主干知识重点考查”的特点

新课标卷每年在立体几何部分均设置三道题目,两道小题共10分,一道大题12分,合计22分,与我们常说的“主干知识重点考查”一致.考查的内容非常稳定:两道小题主要涉及三视图、简单的位置关系、简单的空间角的计算及考生熟悉的几何体的体积、表面积计算等,一道大题一般出现在全卷第18题或第19题的位置,设问一般是两小问,无论文科、理科,第(1)问一般都是垂直关系或平行关系的证明及应用等,第(2)问文科和理科有较大的区别,文科以棱锥的体积、表(侧)面积计算为主,理科以空间角(异面直线的夹角、线面角、二面角)的计算为主,尤其侧重空间向量的应用,体现坐标法的优越性,对学生的计算能力有较高的要求.此外,三道题的整体难度每年都比较稳定,一般是一道简单题与两道中档题,偶尔会有一道题偏难.

2.突出基础性,增强应用性,加强创新能力考查的探索,深入考查分析问题解决问题的能力

为了更好地突出基础性,试题着眼于“立体几何”这一主干知识的基本方法的考查,如文、理科的解答题第(1)问,利用直接证明中最基本的两种证明方法—综合法和分析法证明立体几何中最基本的垂直关系和平行关系,强化对考生的空间想象能力的考查;文科第(2)问每年都是最基本的问题—棱锥的体积、表(侧)面积计算,理科第(2)问每年都是最基本的问题—利用空间向量这一代数工具计算空间角.2017年10月教育部考试中心发布的修订后的《2017年普通高考考试大纲》中提到“对应用意识的考查主要采用解决应用问题的形式.命题时要坚持‘贴近生活,背景公平,控制难度’的原则,试题设计要切合中学数学教学的实际和考生的年龄特点,并结合实践经验,使数学应用问题的难度符合考生的水平”,这是高考试题增强应用性的信号,2017年新课标I卷理科第16题,即是一道以立体几何为载体的应用题,此题是考生熟悉的折叠问题,贴近生活,落脚点是正三棱锥的体积计算,作为小题的压轴题,对于区分不同层次的考生起到了良好的效果,体现出高考“以能力立意为主,突出选拔功能”的思想.《2017年普通高考考试大纲》中还提到“创新意识:能发现问题、提出问题,综合与灵活地应用所学的数学知识、思想方法,选择有效的方法和手段分析信息,进行独立的思考、探索和研究,提出解决问题的思路,创造性地解决问题”,任子朝先生也提出“加强创新能力考查是高考的重要任务”,2015年新课标II卷理科第19题,2016年新课标I卷文科第18题、理科第11题,2017年新课标III卷理科第16题都体现了命题人在创新能力考查这块的良苦用心和探索.

3.经典问题反复考查,不回避热点问题、常见的模型,注重对于数学本质的研究,侧重空间想象能力的考查

2016年新课标I卷文科第18题,以正三棱锥为载体,而这个正三棱锥同时有特殊之处,即三条侧棱两两垂直,考生很快可以联想到立体几何中熟知的“墙角”模型.2017年新课标I卷理科第16题,再次以正三棱锥为载体,考查最基本的正三棱锥的体积计算.2015年新课标II卷理科第6题的三视图以正方体被截去一个“角”为载体,2016年新课标I卷理科第6题的三视图以球被截去部分为载体,何其相似的情境,足见命题人不会“避嫌”.2017年新课标I卷理科第18题,第(2)问中△PAB与△PCB是以PB为公共底边的两个等腰三角形,这是立体几何中的一个常见模型,只需取PB中点E,连结AE,CE,即得到二面角A−PB−C的平面角∠AEC.同样是这个图形,文科的第(2)问中,四面体P−ABD是中国古代数学中称为“鳖臑”的一个重要模型,如果考生熟知“鳖臑”,联想到前文所述的法四,自然水到渠成.当然,2017年新课标II卷文科第15题直接考查长方体的外接球这一教材、课堂上的“常识”,足见命题人对经典问题的情有独钟.因此,新课标卷通过对立体几何中的数学本质的研究来命题,考查空间想象能力,起到了良好的导向作用.

4.在稳定的同时,小心翼翼地尝试改变、创新,体现命题人对高考改革的探索的良苦用心

在2015年的试题中,文科、理科三视图都是“必考题”,而且难度相对较大,尤其是I卷,在2016年,2017年的试题中,三视图慢慢在“迁移”,大致在第6,7题的位置,显然,难度也在变小.然而,更大的变化值得我们重视,理科2017年新课标III卷未考查三视图,文科2017年新课标I卷和III卷均未考查三视图.而2017年新课标III卷理科第16题,考查异面直线的夹角及线面角这一“新颖的”运动最值问题,对考生的空间想象能力提出了更高的要求.

5.在深入考查逻辑推理的同时,不仅没有降低计算量,反而加大了对数学运算这一数学核心素养的考查

认真做完近三年的三视图,可以发现部分试题运算量偏大,甚至繁琐,如2015年,2016年新课标I卷等.此外,解答题的第(2)问对数学运算也有较高的要求,如2016年新课标I卷理科第18题题设给出两个二面角,2017年新课标II卷第19题题设给出一个线面角,2017年新课标III卷理科第19题题设给出“平面AEC把四面体ABCD分成体积相等的两部分”,2017年新课标I卷文科第18题给出四棱锥的体积要求计算侧面积,对考生的运算能力都提出了较高要求.

三、2018年高考立体几何部分的备考建议

基于今年高考评卷过程中出现的典型错误及新课标卷对立体几何部分考查的特点,下面给出如下备考建议,希望对2018届高考备考有所裨益.

(一)回归教材,通读教材,重视立体几何中的概念,加强对立体几何中公理及定理的理解

新课标卷的备考,一定要落在“基础”二字,不论是哪种层次的考生,基础部分的分值至关重要,同时,高考又提出要突出基础性,那么基本的概念,基本的原理,基本的方法自然需要在高三复习中加以重视.2016年新课标I卷文科第18题,以正三棱锥为载体,评卷过程中发现不少考生不清楚正三棱锥的定义和性质,还有很多考生不知道正投影是什么,凸显出考生和一线教师未重视基本概念的复习的不足.2017年新课标I卷文科、理科第18题,第(1)问考查面面垂直的证明,很多考生不知道面面垂直的判定定理,甚至有很多考生不知道线面垂直的判定定理,足见很多考生缺乏对于定理的理解和认识,导致基础题丢分.因此,高三复习一定要重视概念的复习,公理及定理的再理解.

(二)重视立体几何中的基本图形,经典模型及经典结论等

通过对高考真题的研究,复习备考中必须重视向学生灌输立体几何中的基本图形,经典模型及经典结论等,如:①共底边的两个等腰三角形折成的二面角,连接底边上的两条中线,既能得到二面角的平面角,也能得到一组线面垂直;②三组对边分别相等的四面体可以“嵌入”长方体,进一步,正四面体可以“嵌入”正方体;③中国古代数学中提出的“鳖臑”是训练学生证明垂直关系、培养学生空间想象能力的良好素材;④结论“两组对棱分别垂直的四面体,第三组对棱依然垂直”将三垂线定理及其逆定理演绎地淋漓尽致;⑤结论“两个相交平面同时垂直于第三个平面,则两相交平面的交线垂直于第三个平面”是面面垂直的证明题的“分析法利器”;⑥结论“球上任意截面都是圆,圆心与球心的连线垂直于截面”是找多面体的外接球球心的依据等等.

考生如果熟知以上模型及结论,那么在高考中遇到类似或相似的题便能很快找到正确的解题思路,即使遇到所谓的“新题”或难度偏大的题,如能举一反三,依然能做到游刃有余.

(三)认真研究高考方向,把握命题精神,精选题,将学生从题海中解放出来

高考题非常稳定,分值固定,立体几何是“兵家必争之地”,师生必须树立拿下立体几何的信心.老师在高三的复习中,应该精选题,这里的题,既指课堂上的例题,也指周考、月考的考试题.例如三视图的问题,既然高考在有意降低难度,甚至有被取代的趋势,那么这道题的难度就必须严格控制,像个别地方的模拟题在三视图这块就有很多难题,根据最新的高考方向,完全可以删除这些题,真正做到为学生“减负”.同样,2017年新课标III卷理科第16题,我们可以将其与2015年浙江卷理科第8题作比较,即我们不仅要研究新课标卷的真题,而且要适度关注其他省份的高考题出现的“新颖题”,真正提升学生的能力.至于解答题,我们一定要选择反映数学本质的题目,既不在于多新,也不在于多难,关键在于学生通过训练能熟练掌握基本的解题方法,老师通过试题讲解能够将数学本质讲清楚,这样就不会出现理科18题中的典型错误之一:不清楚两个平面的法向量的夹角与二面角的平面角的关系.

(四)深入研究空间向量的算法原理,想方设法为学生的计算量“减负”

新课标卷全卷有一个显著的特点,运算量大,广东省的考生对此心有余悸.在帮助学生提升“数学运算”这一核心素养的过程中,老师除了要亲自板书示范运算过程之外,还应该多些思考,怎样减轻运算量?举个例子,2016年新课标I卷第18题,利用二面角平面角的定义,可以求出公共棱BC的两个法向量

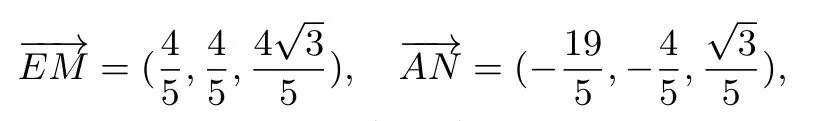
这里的证明限于篇幅,请读者自行思考,此处略去.但是,笔者想强调,“法向量”在求空间角的三角函数值时,关键在于其方向,而其大小,无论如何“伸缩”都不会影响三角函数值.当然,在减轻计算量的道路上,我们还有很多路要走,限于篇幅,本文不再展开讨论.

(五)狠抓规范,强化学生的表达,老师既要严格要求,更要亲自示范

立体几何的解答题,一般都有证明的要求,这既能考查考生的逻辑推理,又能考查考生的数学表达.从今年的评卷情况看,不论是文科生还是理科生,证明题的规范书写都做得不好.主要表现在会证明,但是逻辑混乱;懂原理,但是符号乱用;思路清晰,但是笔误较多,卷面不够整洁.因此,在高三的复习过程中,老师应该对学生的立体几何证明题多一些面批面改,严格要求,另一方面,老师应该在课堂上多一些板书,亲自示范证明题的规范书写.

以上便是笔者对今年高考数学阅卷的总结及对近三年新课标卷立体几何部分试题的分析,希望给出的备考建议能给读者些许启示.

[1]任子朝,陈昂,单旭峰.高考加强创新能力考查的研究[J].教育理论与实践,2017,37(1):29-32.

[2]任子朝,陈昂.高考文理不分科后数学科考试内容改革研究—数学科考试内容改革问卷调查分析[J].数学通报,2015,54(6):1-4.

[3]刘秀湘.2017年高考数学全国卷I试题和答卷分析[J].中学数学研究(上半月),2017(9):9-13.